2012高二物理课件:第二章 第七节 气体实验定律(ⅰ)(粤教版选修3-3)
文档属性
| 名称 | 2012高二物理课件:第二章 第七节 气体实验定律(ⅰ)(粤教版选修3-3) |  | |
| 格式 | zip | ||
| 文件大小 | 267.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 其它版本 | ||
| 科目 | 物理 | ||
| 更新时间 | 2012-08-30 07:39:55 | ||
图片预览






文档简介
(共16张PPT)
第七节 气体实验定律(Ⅰ)
一、气体的状态
温度
体积
压强
反
对于一定质量的气体来说,如果________、________、
________这三个状态参量都不变,我们就说气体处于一定
的状态.
二、玻意耳定律
1.英国科学家玻意耳和法国科学家马略特各自通过实
验发现:一定质量的气体,在温度不变的情况下,压强 p
与体积 V 成________比.这个规律叫做玻意耳定律.
p1V1=p2V2
增大
减小
2.玻意耳定律的表达式:pV=C(常量)或__________.
其中 p1、V1 和 p2、V2 分别表示气体在 1、2 两个不同状态
下的压强和体积.在温度不变时,一定质量的气体,体积
减小时,压强________;体积增大时,压强________.
3.玻意耳定律的微观解释:一定质量的气体,温度保
持不变时,气体分子的平均动能________,气体体积减小,
气体的密集程度________,气体压强________;反之,气
体体积增大,分子密集程度________,气体压强________.
不变
增大
增大
减小
减小
气体等温变化图象
1.p-V 图象
一定质量的气体发生等温变化时的 p—V 图象如图所
示.图线的形状为双曲线.由于它描述的是温度不变时的
p—V 关系,因此称它为等温线.一定质量的气体,不同温
度下的等温线是不同的,图 2-7-1 中 t1图 2-7-1
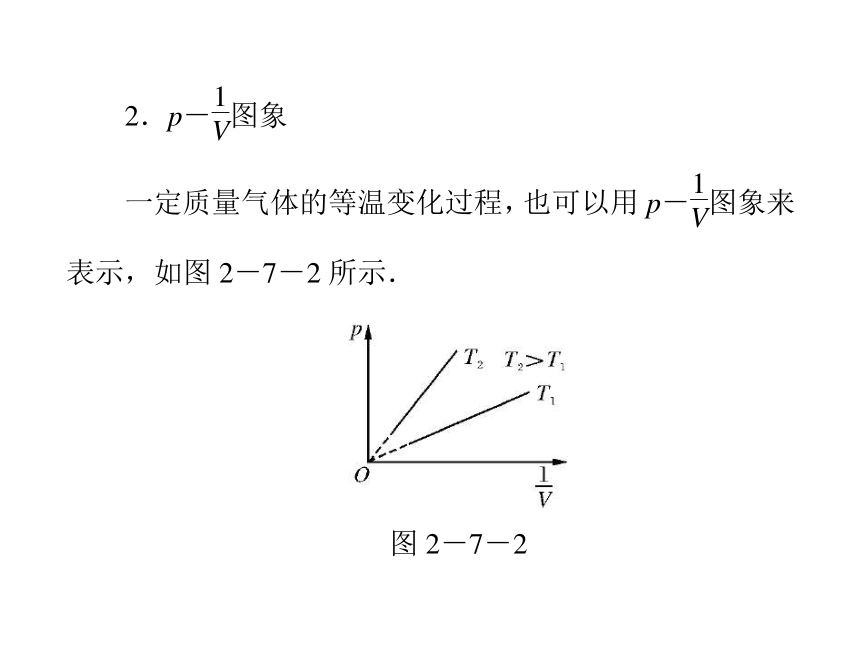
图 2-7-2
理想气体等温变化 p-V 图象
[例 1]一定质量的理想气体由状态 A 变到状态 B 的过
程如图 2-7-3 所示,A、B 位于同一双曲线上,则此变化
过程中,温度(
)
A.一直下降
B.先上升后下降
C.先下降后上升
D.一直上升
图 2-7-3
解析:理想气体等温变化 p-V 图是一条双曲线,称
为等温线,在等温线上的气体的温度都相同,可见 A、B
两个状态温度一定相等,故排除 A 和 D 项;又由于在此等
温线上部的等温线温度高,则气体温度先增加后减少到原
温度.
答案:B
理想气体等温变化的应用
[例 2]如图 2-7-4 所示,是一根一端封闭的粗细均匀
的细玻璃管,用一段 h=19.0 cm 的水银柱将一
部分空气封闭在细玻璃管里.当玻璃管开口向
上竖直放置时(见图甲),管内空气柱长 L1=15.0
cm,当时的大气压强为 p0=1.01×105 Pa.那么,
当玻璃管开口向下竖直放置时(见图乙),管内
空气柱的长度该是多少?
图 2-7-4
解析:基本思路:(1)明确研究对象为一定质量的气体;
(2)分析过程是否等温;(3)写出变化前后的 p 和 V 的值或表
达式;(4)确定变化前后的 p 和 V 单位统一;(5)根据 p1V1
=p2V2 解题.
设细玻璃管横截面积为 S,设变化后空气柱的长度为 L2,
变化前空气的体积 V1=L1S
压强 p1=p0+ph=(76+19) cmHg=95 cmHg
变化后空气的体积 V2=L2S
压强 p2=p0-ph=(76-19) cmHg=57 cmHg
根据玻意耳定律 p1V1=p2V2,代入数值得到结果 L2=
25 cm.
[例 3]如图 2-7-5 所示,粗细均匀的 U 形玻璃管,
右端开口,左端封闭,管内用水银将一部分空气封闭在管
中,开口朝上竖直放置时,被封闭的空气柱长 24 cm,两
边水银高度差为 15 cm,若大气压强为 75 cmHg,问再向
开口端倒入长为 46 cm 的水银柱时,封闭端空气柱长度将
是多少?
图 2-7-5
解:倒入水银前对封闭端的气体有:
V1=SL1=24S
p1=(75-15) cmHg=60 cmHg
倒入水银后,左端水银面将上升,右端水银面将下降,
设左端水银面上升 x,则此时封闭端气柱长
L2=L1-x=24-x
此时两边水银面的高度差
Δh2=46-(15+2x)=2L2-17
此时封闭端气体的压强为
p2=75+Δh2=58+2L2
根据玻意耳定律 p1V1=p2V2
得 24×60=(58+2L2)×L2
解得:L2=-45 cm(舍去),L2=16 cm.
方法规律:应用玻意耳定律解题时,关键是找出气体
初始状态的状态参量(p1,V1)和末状态对应的状态参量(p2,
V2),然后应用玻意耳定律的表达式列方程即可.
应用玻意耳定律解题的一般步骤:
(1)确定研究对象,判断是否满足玻意耳定律的条件;
(2)确定始末状态及状态参量(p1、V1、p2、V2);
(3)根据玻意耳定律列方程求解.
图 2-7-6
答案:G′=p0S+G
返回
第七节 气体实验定律(Ⅰ)
一、气体的状态
温度
体积
压强
反
对于一定质量的气体来说,如果________、________、
________这三个状态参量都不变,我们就说气体处于一定
的状态.
二、玻意耳定律
1.英国科学家玻意耳和法国科学家马略特各自通过实
验发现:一定质量的气体,在温度不变的情况下,压强 p
与体积 V 成________比.这个规律叫做玻意耳定律.
p1V1=p2V2
增大
减小
2.玻意耳定律的表达式:pV=C(常量)或__________.
其中 p1、V1 和 p2、V2 分别表示气体在 1、2 两个不同状态
下的压强和体积.在温度不变时,一定质量的气体,体积
减小时,压强________;体积增大时,压强________.
3.玻意耳定律的微观解释:一定质量的气体,温度保
持不变时,气体分子的平均动能________,气体体积减小,
气体的密集程度________,气体压强________;反之,气
体体积增大,分子密集程度________,气体压强________.
不变
增大
增大
减小
减小
气体等温变化图象
1.p-V 图象
一定质量的气体发生等温变化时的 p—V 图象如图所
示.图线的形状为双曲线.由于它描述的是温度不变时的
p—V 关系,因此称它为等温线.一定质量的气体,不同温
度下的等温线是不同的,图 2-7-1 中 t1
图 2-7-2
理想气体等温变化 p-V 图象
[例 1]一定质量的理想气体由状态 A 变到状态 B 的过
程如图 2-7-3 所示,A、B 位于同一双曲线上,则此变化
过程中,温度(
)
A.一直下降
B.先上升后下降
C.先下降后上升
D.一直上升
图 2-7-3
解析:理想气体等温变化 p-V 图是一条双曲线,称
为等温线,在等温线上的气体的温度都相同,可见 A、B
两个状态温度一定相等,故排除 A 和 D 项;又由于在此等
温线上部的等温线温度高,则气体温度先增加后减少到原
温度.
答案:B
理想气体等温变化的应用
[例 2]如图 2-7-4 所示,是一根一端封闭的粗细均匀
的细玻璃管,用一段 h=19.0 cm 的水银柱将一
部分空气封闭在细玻璃管里.当玻璃管开口向
上竖直放置时(见图甲),管内空气柱长 L1=15.0
cm,当时的大气压强为 p0=1.01×105 Pa.那么,
当玻璃管开口向下竖直放置时(见图乙),管内
空气柱的长度该是多少?
图 2-7-4
解析:基本思路:(1)明确研究对象为一定质量的气体;
(2)分析过程是否等温;(3)写出变化前后的 p 和 V 的值或表
达式;(4)确定变化前后的 p 和 V 单位统一;(5)根据 p1V1
=p2V2 解题.
设细玻璃管横截面积为 S,设变化后空气柱的长度为 L2,
变化前空气的体积 V1=L1S
压强 p1=p0+ph=(76+19) cmHg=95 cmHg
变化后空气的体积 V2=L2S
压强 p2=p0-ph=(76-19) cmHg=57 cmHg
根据玻意耳定律 p1V1=p2V2,代入数值得到结果 L2=
25 cm.
[例 3]如图 2-7-5 所示,粗细均匀的 U 形玻璃管,
右端开口,左端封闭,管内用水银将一部分空气封闭在管
中,开口朝上竖直放置时,被封闭的空气柱长 24 cm,两
边水银高度差为 15 cm,若大气压强为 75 cmHg,问再向
开口端倒入长为 46 cm 的水银柱时,封闭端空气柱长度将
是多少?
图 2-7-5
解:倒入水银前对封闭端的气体有:
V1=SL1=24S
p1=(75-15) cmHg=60 cmHg
倒入水银后,左端水银面将上升,右端水银面将下降,
设左端水银面上升 x,则此时封闭端气柱长
L2=L1-x=24-x
此时两边水银面的高度差
Δh2=46-(15+2x)=2L2-17
此时封闭端气体的压强为
p2=75+Δh2=58+2L2
根据玻意耳定律 p1V1=p2V2
得 24×60=(58+2L2)×L2
解得:L2=-45 cm(舍去),L2=16 cm.
方法规律:应用玻意耳定律解题时,关键是找出气体
初始状态的状态参量(p1,V1)和末状态对应的状态参量(p2,
V2),然后应用玻意耳定律的表达式列方程即可.
应用玻意耳定律解题的一般步骤:
(1)确定研究对象,判断是否满足玻意耳定律的条件;
(2)确定始末状态及状态参量(p1、V1、p2、V2);
(3)根据玻意耳定律列方程求解.
图 2-7-6
答案:G′=p0S+G
返回
同课章节目录
