2012高二物理课件:第一章 章末整合 (粤教版选修3-2)
文档属性
| 名称 | 2012高二物理课件:第一章 章末整合 (粤教版选修3-2) |

|
|
| 格式 | zip | ||
| 文件大小 | 614.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 其它版本 | ||
| 科目 | 物理 | ||
| 更新时间 | 2012-08-30 07:39:55 | ||
图片预览









文档简介
(共30张PPT)
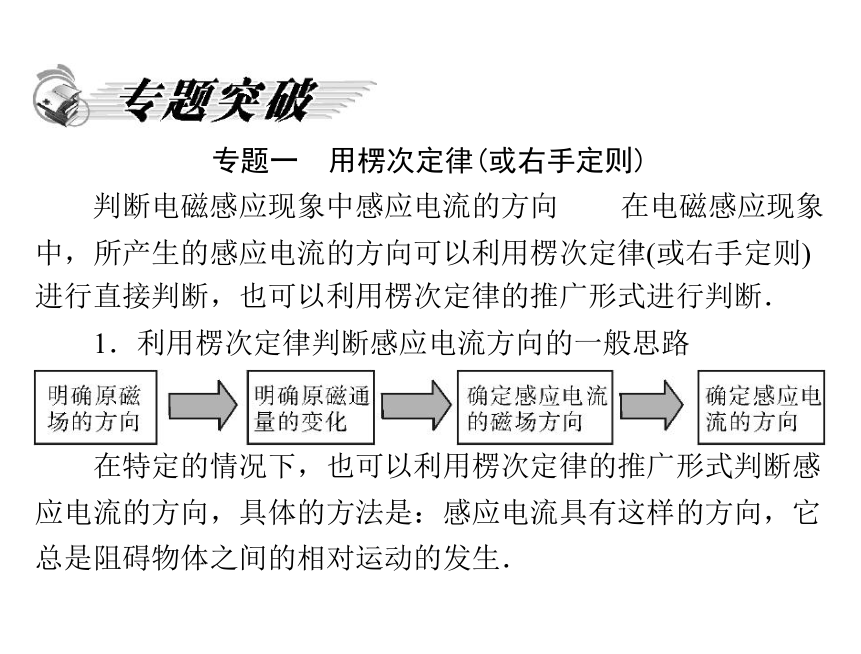
专题一 用楞次定律(或右手定则)
判断电磁感应现象中感应电流的方向
在电磁感应现象
中,所产生的感应电流的方向可以利用楞次定律(或右手定则)
进行直接判断,也可以利用楞次定律的推广形式进行判断.
1.利用楞次定律判断感应电流方向的一般思路
在特定的情况下,也可以利用楞次定律的推广形式判断感
应电流的方向,具体的方法是:感应电流具有这样的方向,它
总是阻碍物体之间的相对运动的发生.
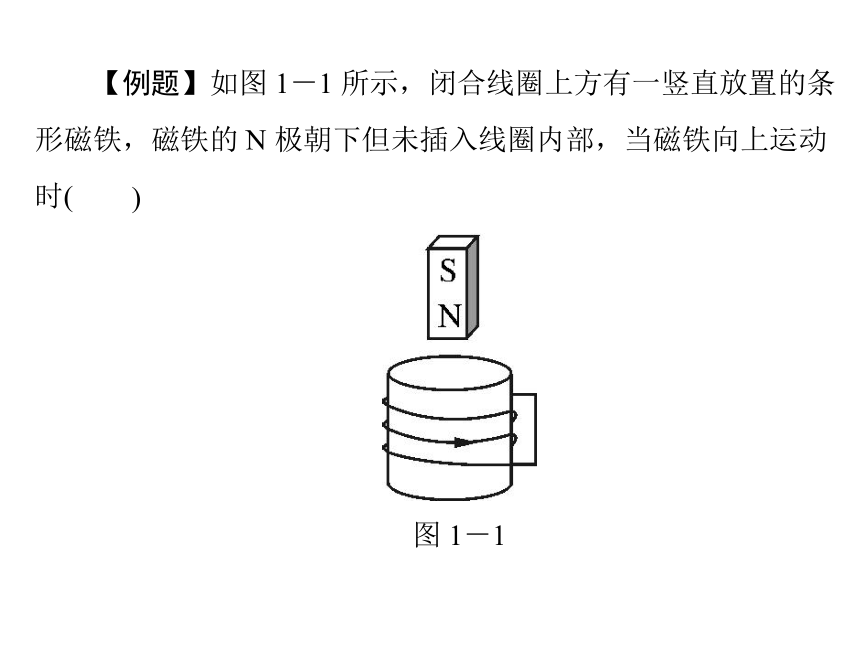
【例题】如图 1-1 所示,闭合线圈上方有一竖直放置的条
形磁铁,磁铁的 N 极朝下但未插入线圈内部,当磁铁向上运动
时(
)
图 1-1
A.线圈中感应电流的方向与图中箭头方向相同,磁铁与
线圈相互吸引
B.线圈中感应电流的方向与图中箭头方向相同,磁铁与
线圈相互排斥
C.线圈中感应电流的方向与图中箭头方向相反,磁铁与
线圈相互吸引
D.线圈中感应电流的方向与图中箭头方向相反,磁铁与
线圈相互排斥
解析:磁铁的 N 极下方区域的磁感线向下,因此,磁铁的
N 极朝下但未插入线圈内部时,穿过线圈的磁场方向向下,穿
过线圈的磁感线指向向下,当磁铁向上运动时,穿过线圈的磁
通量的变化是:向下减小,根据楞次定律,闭合线圈中会产生
感应电流,电流的磁场方向应向下(补充磁通量减小),再根据
安培定则,可以判断,线圈中感应电流的方向与图中箭头方向
相反,且磁铁与线圈相互吸引.
答案:C
2.利用右手定则判断感应电流方向的一般思路
【例题】如图 1-2 所示,CDEF 是金属框,当导体 AB 向
右移动时,有关导体 AB 中的电流方向,下列说法中正确的是
(
)
图 1-2
A.导体 AB 中无感应电流
B.感应电流方向先从 A→B,后从 B→A
C.感应电流方向从 A→B
D.感应电流方向从 B→A
解析:导体AB 中有感应电流,根据右手定则,感应电流
方向从 A→B,而CD 中电流的方向为C→D,EF 中电流的方向
为 F→E.
答案:C
专题二
用法拉第电磁感应定律进行计算
在电磁感应现象中,闭合回路中因磁通量发生变化会产生
感应电流,就其本质而言,是在电磁感应现象中,回路中产生
了感应电动势,如果回路是闭合的,回路中就会有感应电流,
如果回路不是闭合的,则回路中没有感应电流,但感应电动势
仍然是存在的,感应电动势的大小计算可以利用法拉第电磁感
应定律进行计算,而闭合回路中的感应电流则可以利用欧姆定
律计算,这类问题也是本章的重点,由于感应电流产生的过程
伴随着有能量的转化,因此,在电磁感应现象中,也存在能量
守恒定律的应用.
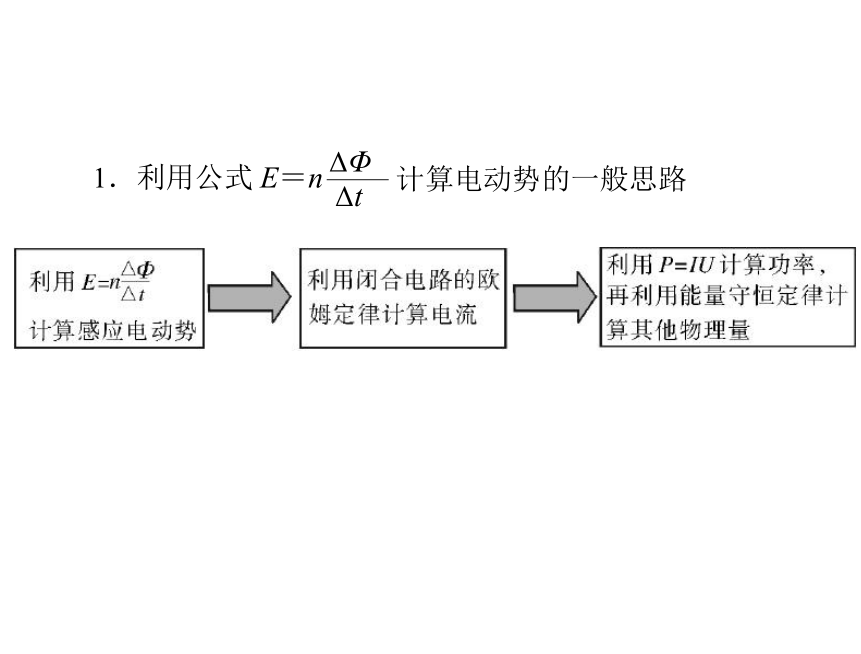
计算电动势的一般思路
1.利用公式 E=n
ΔΦ
Δt
【例题】 如图 1-3 所示,两根电阻不计,间距为 l 的平
行金属导轨,一端接有阻值为 R 的电阻,导轨上垂直搁置一根
质量为 m、电阻为 r 的金属棒,整个装置处于竖直向上磁感强
度为 B 的匀强磁场中.现给金属棒施一冲量,使它以初速 v0 向
左滑行.设棒与导轨间的动摩擦因数为μ,金属棒从开始运动到
停止的整个过程中,通过电阻 R 的电量为 q.求:(导轨足够长)
(1)金属棒沿导轨滑行的距离.
(2)在运动的整个过程中消耗的电能.
图 1-3
答案:见解析
2.利用导体做切割磁感线运动产生的感应电动势 E=BLv
进行计算的一般思路
在公式 E=BLv 的应用中,必须注意:
(1)公式 E=BLv 只适用于导体做切割磁感线运动(平动)而
产生的感应电动势的计算,且磁场是匀强磁场,导体的运动方
向与磁场方向垂直,L 是切割磁感线的有效长度.
(2)当导体的运动方向与磁场方向间的夹角为θ时,则 E=
BLvsin θ.
【例题】 如图 1-4 所示,直角三角形导线框 abc 固定在匀
强磁场中,ab 是一段长为 L、电阻为 R 的均匀导线,ac 和 bc 的
电阻可不计,ac 长度为 L/2.磁场的磁感强度为 B,方向垂直于纸
面向里.现有一段长度为 L/2、电阻为 R/2 的均匀导体杆 MN 架
在导线框上,开始时紧靠 ac,然后沿 ac 方向以恒定速度 v 向 b
端滑动,滑动中始终与 ac 平行并与导线框保持良好接触.当 MN
滑过的距离为 L/3 时,导线 ac 中的电流是多大?方向如何?
图 1-4
解析:MN 滑过的距离为 L/3 时,它与 bc 的接触点为 P,
如图所示由几何关系可知 MP 长度为 L/3,MP 中的感应电动势
根据右手定则,MP 中的感应电流的方向由 P 流向 M,所
以电流 Iac 的方向由 a 流向 c.
答案:见解析
1.(双选,2011年山东卷)如图1-5所示,两固定的竖直光滑金属导轨足够长且电阻不计.两质量、长度均相同的导体棒c、d,置于边界水平的匀强磁场上方同一高度h处.磁场宽为3h,方向与导轨平面垂直.先由静止释放c,c刚进入磁场即匀速运动,此时再由静止释放d,两导体棒与导轨始终保持良好接触.用ac表示c的加速度,Ekd表示d的动能,xc、xd分别表示c、d相对释放点的位移.则以下四个图象中正确的是( )
图 1-5
加速度为0,在d下落h的过程中,h=—gt2,c匀速下降了xc
解析:开始时 c 的加速度为 g,c 刚进入磁场即匀速运动,
1
2
=gt·t=2h,d 进入磁场后,c、d 又只在重力作用下运动,加速
度为g,一起运动了h,c 出磁场,这时c 的加速度仍为g,因
此 A 错误,B 正确;c 出磁场后,d 这时受到重力和向上的安培
力,并且合力向上,开始做减速运动,当运动了2h 后,d 出磁
场,又做加速运动,所以C 错误,D 正确.
答案:BD
2.(2011 年浙江卷)如图 1-6 甲所示,在水平面上固定有
长为 L=2 m、宽为 d=1 m 的金属“U”形导轨,在“U”形导轨右
侧 l=0.5 m 范围内存在垂直纸面向里的匀强磁场,且磁感应强
度随时间变化规律如图乙所示.在 t=0 时刻,质量为 m=0.1 kg
的导体棒以 v0=1 m/s 的初速度从导轨的左端开始向右运动,导
体棒与导轨之间的动摩擦因数为μ=0.1,导轨与导体棒单位长
度的电阻均为λ=0.1 Ω/m,不计导体棒与导轨之间的接触电阻
及地球磁场的影响(取 g=10 m/s2).
(1)通过计算分析 4 s 内导体棒的运动情况;
(2)计算 4 s 内回路中电流的大小,并判断电流方向;
(3)计算 4 s 内回路产生的焦耳热.
图 1-6
解:(1)导体棒先在无磁场区域做匀减速运动,有
代入数据解得:t=1 s,x=0.5 m,导体棒没有进入磁场区
域.
导体棒在 1 s 末已经停止运动,以后一直保持静止,离左端
位置仍为 x=0.5 m.
(2)前 2 s 磁通量不变,回路电动势和电流分别为 E=0,I=0
回路的总长度为 5 m,因此回路的总电阻为 R=5λ=0.5 Ω
根据楞次定律,在回路中的电流方向是顺时针方向.
(3)前 2 s 电流为零,后 2 s 有恒定电流,焦耳热为
Q=I2Rt=0.04 J.
3.(2010 年广东卷)如图 1-7 所示,平行导轨间有一矩形
的匀强磁场区域,细金属棒 PQ 沿导轨从 MN 处匀速运动到
M′N′的过程中,棒上感应电动势 E 随时间 t 变化的图示,可
能正确的是(
)
图 1-7
解析:导线做匀速直线运动切割磁感线时,E=BLv,是常
数.开始没有切割磁感线,就没有电动势,最后一段也没有切
割.
答案:A
4.(2010 年新课标卷)如图 1-8 所示,两个端面半径同为
R 的圆柱形铁芯同轴水平放置,相对的端面之间有一缝隙,铁
芯上绕导线并与电源连接,在缝隙中形成一匀强磁场.一铜质
细直棒 ab 水平置于缝隙中,且与圆柱轴线等高、垂直.让铜棒
从静止开始自由下落,铜棒下落距离为 0.2R 时铜棒中电动势大
小为 E1,下落距离为 0.8R 时电动势大小为 E2.忽略涡流损耗和
边缘效应,关于 E1、E2 的大小和铜棒离开磁场前两端的极性,
下列判断正确的是(
)
图 1-8
A.E1>E2,a 端为正
B.E1>E2,b 端为正
C.E1D.E1答案:D
5.(2010 年江苏卷)如图 1-9 所示,两足够长的光滑金属
导轨竖直放置,相距为 L, 一理想电流表与两导轨相连,匀强磁
场与导轨平面垂直.一质量为 m、有效电阻为 R 的导体棒在距
磁场上边界 h 处静止释放.导体棒进入磁场后,流经电流表的
电流逐渐减小,最终稳定为 I.整个运动过程中,导体棒与导轨
接触良好,且始终保持水平,不计导轨的电阻.
求:
(1)磁感应强度的大小 B.
(2)电流稳定后,导体棒运动速度的大小 v.
(3)流经电流表电流的最大值.
图 1-9
专题一 用楞次定律(或右手定则)
判断电磁感应现象中感应电流的方向
在电磁感应现象
中,所产生的感应电流的方向可以利用楞次定律(或右手定则)
进行直接判断,也可以利用楞次定律的推广形式进行判断.
1.利用楞次定律判断感应电流方向的一般思路
在特定的情况下,也可以利用楞次定律的推广形式判断感
应电流的方向,具体的方法是:感应电流具有这样的方向,它
总是阻碍物体之间的相对运动的发生.
【例题】如图 1-1 所示,闭合线圈上方有一竖直放置的条
形磁铁,磁铁的 N 极朝下但未插入线圈内部,当磁铁向上运动
时(
)
图 1-1
A.线圈中感应电流的方向与图中箭头方向相同,磁铁与
线圈相互吸引
B.线圈中感应电流的方向与图中箭头方向相同,磁铁与
线圈相互排斥
C.线圈中感应电流的方向与图中箭头方向相反,磁铁与
线圈相互吸引
D.线圈中感应电流的方向与图中箭头方向相反,磁铁与
线圈相互排斥
解析:磁铁的 N 极下方区域的磁感线向下,因此,磁铁的
N 极朝下但未插入线圈内部时,穿过线圈的磁场方向向下,穿
过线圈的磁感线指向向下,当磁铁向上运动时,穿过线圈的磁
通量的变化是:向下减小,根据楞次定律,闭合线圈中会产生
感应电流,电流的磁场方向应向下(补充磁通量减小),再根据
安培定则,可以判断,线圈中感应电流的方向与图中箭头方向
相反,且磁铁与线圈相互吸引.
答案:C
2.利用右手定则判断感应电流方向的一般思路
【例题】如图 1-2 所示,CDEF 是金属框,当导体 AB 向
右移动时,有关导体 AB 中的电流方向,下列说法中正确的是
(
)
图 1-2
A.导体 AB 中无感应电流
B.感应电流方向先从 A→B,后从 B→A
C.感应电流方向从 A→B
D.感应电流方向从 B→A
解析:导体AB 中有感应电流,根据右手定则,感应电流
方向从 A→B,而CD 中电流的方向为C→D,EF 中电流的方向
为 F→E.
答案:C
专题二
用法拉第电磁感应定律进行计算
在电磁感应现象中,闭合回路中因磁通量发生变化会产生
感应电流,就其本质而言,是在电磁感应现象中,回路中产生
了感应电动势,如果回路是闭合的,回路中就会有感应电流,
如果回路不是闭合的,则回路中没有感应电流,但感应电动势
仍然是存在的,感应电动势的大小计算可以利用法拉第电磁感
应定律进行计算,而闭合回路中的感应电流则可以利用欧姆定
律计算,这类问题也是本章的重点,由于感应电流产生的过程
伴随着有能量的转化,因此,在电磁感应现象中,也存在能量
守恒定律的应用.
计算电动势的一般思路
1.利用公式 E=n
ΔΦ
Δt
【例题】 如图 1-3 所示,两根电阻不计,间距为 l 的平
行金属导轨,一端接有阻值为 R 的电阻,导轨上垂直搁置一根
质量为 m、电阻为 r 的金属棒,整个装置处于竖直向上磁感强
度为 B 的匀强磁场中.现给金属棒施一冲量,使它以初速 v0 向
左滑行.设棒与导轨间的动摩擦因数为μ,金属棒从开始运动到
停止的整个过程中,通过电阻 R 的电量为 q.求:(导轨足够长)
(1)金属棒沿导轨滑行的距离.
(2)在运动的整个过程中消耗的电能.
图 1-3
答案:见解析
2.利用导体做切割磁感线运动产生的感应电动势 E=BLv
进行计算的一般思路
在公式 E=BLv 的应用中,必须注意:
(1)公式 E=BLv 只适用于导体做切割磁感线运动(平动)而
产生的感应电动势的计算,且磁场是匀强磁场,导体的运动方
向与磁场方向垂直,L 是切割磁感线的有效长度.
(2)当导体的运动方向与磁场方向间的夹角为θ时,则 E=
BLvsin θ.
【例题】 如图 1-4 所示,直角三角形导线框 abc 固定在匀
强磁场中,ab 是一段长为 L、电阻为 R 的均匀导线,ac 和 bc 的
电阻可不计,ac 长度为 L/2.磁场的磁感强度为 B,方向垂直于纸
面向里.现有一段长度为 L/2、电阻为 R/2 的均匀导体杆 MN 架
在导线框上,开始时紧靠 ac,然后沿 ac 方向以恒定速度 v 向 b
端滑动,滑动中始终与 ac 平行并与导线框保持良好接触.当 MN
滑过的距离为 L/3 时,导线 ac 中的电流是多大?方向如何?
图 1-4
解析:MN 滑过的距离为 L/3 时,它与 bc 的接触点为 P,
如图所示由几何关系可知 MP 长度为 L/3,MP 中的感应电动势
根据右手定则,MP 中的感应电流的方向由 P 流向 M,所
以电流 Iac 的方向由 a 流向 c.
答案:见解析
1.(双选,2011年山东卷)如图1-5所示,两固定的竖直光滑金属导轨足够长且电阻不计.两质量、长度均相同的导体棒c、d,置于边界水平的匀强磁场上方同一高度h处.磁场宽为3h,方向与导轨平面垂直.先由静止释放c,c刚进入磁场即匀速运动,此时再由静止释放d,两导体棒与导轨始终保持良好接触.用ac表示c的加速度,Ekd表示d的动能,xc、xd分别表示c、d相对释放点的位移.则以下四个图象中正确的是( )
图 1-5
加速度为0,在d下落h的过程中,h=—gt2,c匀速下降了xc
解析:开始时 c 的加速度为 g,c 刚进入磁场即匀速运动,
1
2
=gt·t=2h,d 进入磁场后,c、d 又只在重力作用下运动,加速
度为g,一起运动了h,c 出磁场,这时c 的加速度仍为g,因
此 A 错误,B 正确;c 出磁场后,d 这时受到重力和向上的安培
力,并且合力向上,开始做减速运动,当运动了2h 后,d 出磁
场,又做加速运动,所以C 错误,D 正确.
答案:BD
2.(2011 年浙江卷)如图 1-6 甲所示,在水平面上固定有
长为 L=2 m、宽为 d=1 m 的金属“U”形导轨,在“U”形导轨右
侧 l=0.5 m 范围内存在垂直纸面向里的匀强磁场,且磁感应强
度随时间变化规律如图乙所示.在 t=0 时刻,质量为 m=0.1 kg
的导体棒以 v0=1 m/s 的初速度从导轨的左端开始向右运动,导
体棒与导轨之间的动摩擦因数为μ=0.1,导轨与导体棒单位长
度的电阻均为λ=0.1 Ω/m,不计导体棒与导轨之间的接触电阻
及地球磁场的影响(取 g=10 m/s2).
(1)通过计算分析 4 s 内导体棒的运动情况;
(2)计算 4 s 内回路中电流的大小,并判断电流方向;
(3)计算 4 s 内回路产生的焦耳热.
图 1-6
解:(1)导体棒先在无磁场区域做匀减速运动,有
代入数据解得:t=1 s,x=0.5 m,导体棒没有进入磁场区
域.
导体棒在 1 s 末已经停止运动,以后一直保持静止,离左端
位置仍为 x=0.5 m.
(2)前 2 s 磁通量不变,回路电动势和电流分别为 E=0,I=0
回路的总长度为 5 m,因此回路的总电阻为 R=5λ=0.5 Ω
根据楞次定律,在回路中的电流方向是顺时针方向.
(3)前 2 s 电流为零,后 2 s 有恒定电流,焦耳热为
Q=I2Rt=0.04 J.
3.(2010 年广东卷)如图 1-7 所示,平行导轨间有一矩形
的匀强磁场区域,细金属棒 PQ 沿导轨从 MN 处匀速运动到
M′N′的过程中,棒上感应电动势 E 随时间 t 变化的图示,可
能正确的是(
)
图 1-7
解析:导线做匀速直线运动切割磁感线时,E=BLv,是常
数.开始没有切割磁感线,就没有电动势,最后一段也没有切
割.
答案:A
4.(2010 年新课标卷)如图 1-8 所示,两个端面半径同为
R 的圆柱形铁芯同轴水平放置,相对的端面之间有一缝隙,铁
芯上绕导线并与电源连接,在缝隙中形成一匀强磁场.一铜质
细直棒 ab 水平置于缝隙中,且与圆柱轴线等高、垂直.让铜棒
从静止开始自由下落,铜棒下落距离为 0.2R 时铜棒中电动势大
小为 E1,下落距离为 0.8R 时电动势大小为 E2.忽略涡流损耗和
边缘效应,关于 E1、E2 的大小和铜棒离开磁场前两端的极性,
下列判断正确的是(
)
图 1-8
A.E1>E2,a 端为正
B.E1>E2,b 端为正
C.E1
5.(2010 年江苏卷)如图 1-9 所示,两足够长的光滑金属
导轨竖直放置,相距为 L, 一理想电流表与两导轨相连,匀强磁
场与导轨平面垂直.一质量为 m、有效电阻为 R 的导体棒在距
磁场上边界 h 处静止释放.导体棒进入磁场后,流经电流表的
电流逐渐减小,最终稳定为 I.整个运动过程中,导体棒与导轨
接触良好,且始终保持水平,不计导轨的电阻.
求:
(1)磁感应强度的大小 B.
(2)电流稳定后,导体棒运动速度的大小 v.
(3)流经电流表电流的最大值.
图 1-9
同课章节目录
