全等三角形复习导学案(无答案)
文档属性
| 名称 | 全等三角形复习导学案(无答案) | 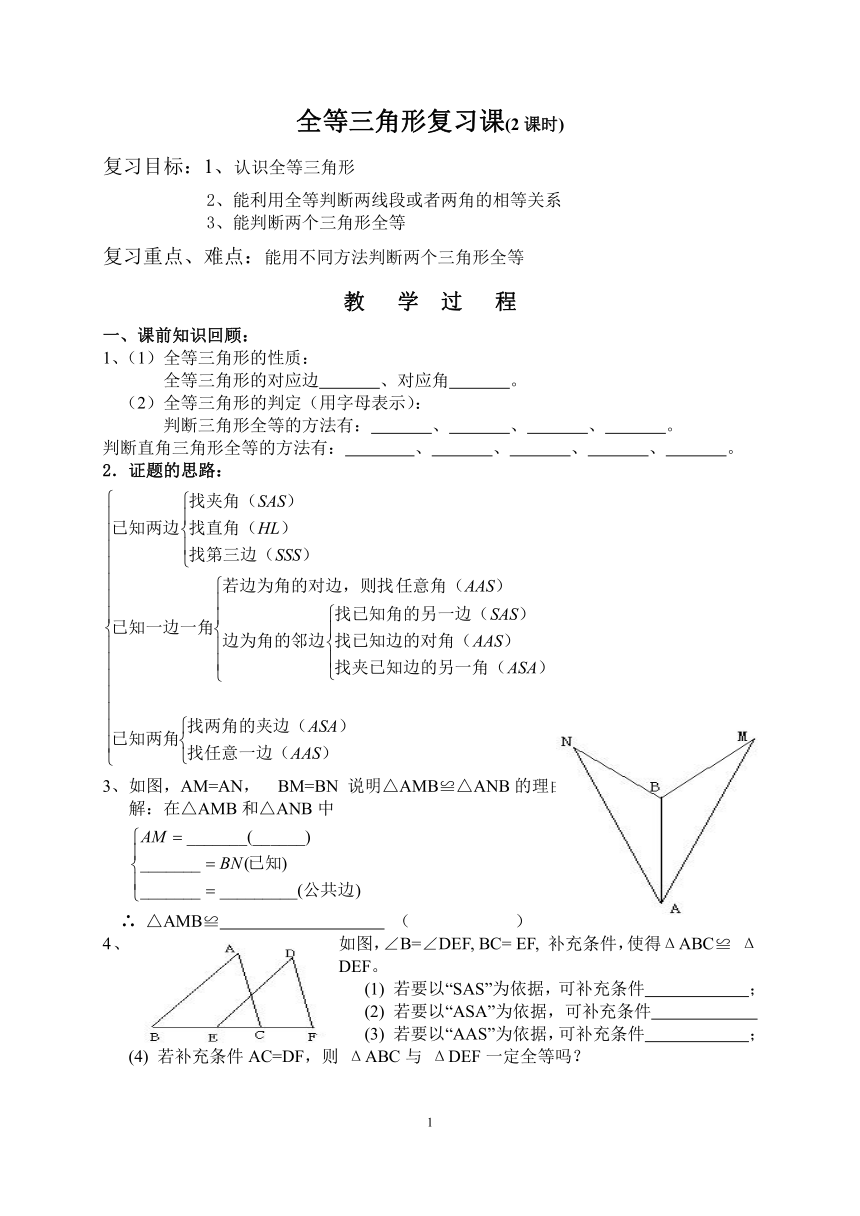 | |
| 格式 | zip | ||
| 文件大小 | 60.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-08-30 07:47:21 | ||
图片预览

文档简介
全等三角形复习课(2课时)
复习目标:1、认识全等三角形
2、能利用全等判断两线段或者两角的相等关系
3、能判断两个三角形全等
复习重点、难点:能用不同方法判断两个三角形全等
教 学 过 程
一、课前知识回顾:
1、(1)全等三角形的性质:
全等三角形的对应边 、对应角 。
(2)全等三角形的判定(用字母表示):
判断三角形全等的方法有: 、 、 、 。
判断直角三角形全等的方法有: 、 、 、 、 。
2.证题的思路:
3、如图,AM=AN, BM=BN 说明△AMB≌△ANB的理由。
解:在△AMB和△ANB中
∴ △AMB≌ ( )
4、 如图,∠B=∠DEF, BC= EF, 补充条件,使得ΔABC≌ ΔDEF。
(1) 若要以“SAS”为依据,可补充条件 ;
(2) 若要以“ASA”为依据,可补充条件
(3) 若要以“AAS”为依据,可补充条件 ;
(4) 若补充条件AC=DF,则 ΔABC与 ΔDEF一定全等吗?
二、合作与探究
1,两个能够完全重合的图形称为 .全等图形的 和 完全相同.
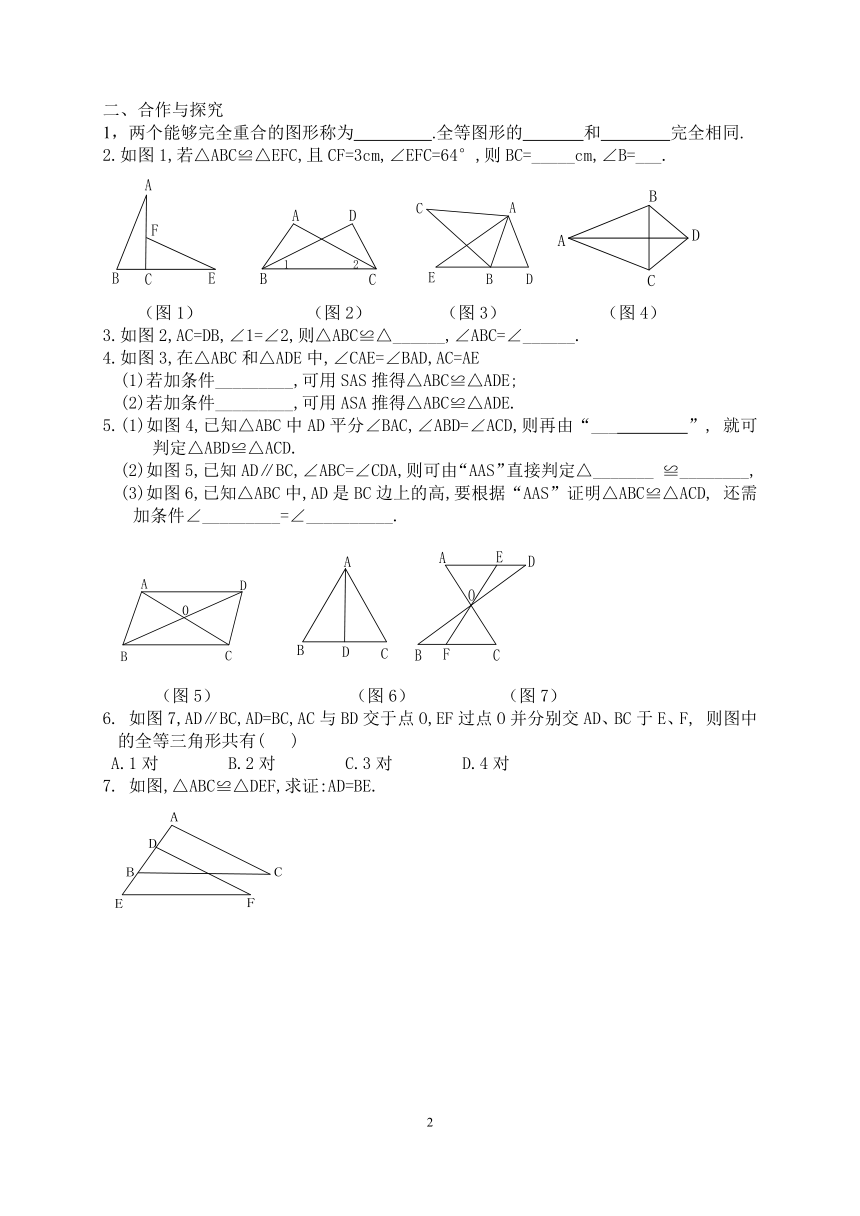
2.如图1,若△ABC≌△EFC,且CF=3cm,∠EFC=64°,则BC=_____cm,∠B=___.毛
(图1) (图2) (图3) (图4)
3.如图2,AC=DB,∠1=∠2,则△ABC≌△______,∠ABC=∠______.
4.如图3,在△ABC和△ADE中,∠CAE=∠BAD,AC=AE
(1)若加条件_________,可用SAS推得△ABC≌△ADE;
(2)若加条件_________,可用ASA推得△ABC≌△ADE.
5.(1)如图4,已知△ABC中AD平分∠BAC,∠ABD=∠ACD,则再由“___ ”, 就可判定△ABD≌△ACD.
(2)如图5,已知AD∥BC,∠ABC=∠CDA,则可由“AAS”直接判定△_______ ≌________,
(3)如图6,已知△ABC中,AD是BC边上的高,要根据“AAS”证明△ABC≌△ACD, 还需加条件∠_________=∠__________.
(图5) (图6) (图7)
6. 如图7,AD∥BC,AD=BC,AC与BD交于点O,EF过点O并分别交AD、BC于E、F, 则图中的全等三角形共有( )
A.1对 B.2对 C.3对 D.4对
7. 如图,△ABC≌△DEF,求证:AD=BE.
8.如图,CD⊥AB,BE⊥AC,垂足分别为D、E,BE交CD于F,且AD=DF,求证:AC= BF.
9. 如图,已知:AC和BD相交于点O,OA=OC,OB=OD,AB与DC平行吗?
说明理由。
10、如图:已知AB=AE,BC=ED,∠B=∠E,AF⊥CD,F为垂足,
求证: ① AC=AD; ②CF=DF。
11、如图,已知∠A=90°,AB=BD,ED⊥BC于D,在图中找出另外一对相等的线段吗?为什么?
12、.在△ABC中,,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E(1)当直线MN绕点C旋转到图①的位置时,求证:DE=AD+BE
(2)当直线MN绕点C旋转到图②的位置时,求证:DE=AD-BE
(3)当直线MN绕点C旋转到图③的位置时,试问:DE、AD、BE有怎样的等量关系 请写出这个等量关系,并加以证明
A
B
C
D
O
4
复习目标:1、认识全等三角形
2、能利用全等判断两线段或者两角的相等关系
3、能判断两个三角形全等
复习重点、难点:能用不同方法判断两个三角形全等
教 学 过 程
一、课前知识回顾:
1、(1)全等三角形的性质:
全等三角形的对应边 、对应角 。
(2)全等三角形的判定(用字母表示):
判断三角形全等的方法有: 、 、 、 。
判断直角三角形全等的方法有: 、 、 、 、 。
2.证题的思路:
3、如图,AM=AN, BM=BN 说明△AMB≌△ANB的理由。
解:在△AMB和△ANB中
∴ △AMB≌ ( )
4、 如图,∠B=∠DEF, BC= EF, 补充条件,使得ΔABC≌ ΔDEF。
(1) 若要以“SAS”为依据,可补充条件 ;
(2) 若要以“ASA”为依据,可补充条件
(3) 若要以“AAS”为依据,可补充条件 ;
(4) 若补充条件AC=DF,则 ΔABC与 ΔDEF一定全等吗?
二、合作与探究
1,两个能够完全重合的图形称为 .全等图形的 和 完全相同.
2.如图1,若△ABC≌△EFC,且CF=3cm,∠EFC=64°,则BC=_____cm,∠B=___.毛
(图1) (图2) (图3) (图4)
3.如图2,AC=DB,∠1=∠2,则△ABC≌△______,∠ABC=∠______.
4.如图3,在△ABC和△ADE中,∠CAE=∠BAD,AC=AE
(1)若加条件_________,可用SAS推得△ABC≌△ADE;
(2)若加条件_________,可用ASA推得△ABC≌△ADE.
5.(1)如图4,已知△ABC中AD平分∠BAC,∠ABD=∠ACD,则再由“___ ”, 就可判定△ABD≌△ACD.
(2)如图5,已知AD∥BC,∠ABC=∠CDA,则可由“AAS”直接判定△_______ ≌________,
(3)如图6,已知△ABC中,AD是BC边上的高,要根据“AAS”证明△ABC≌△ACD, 还需加条件∠_________=∠__________.
(图5) (图6) (图7)
6. 如图7,AD∥BC,AD=BC,AC与BD交于点O,EF过点O并分别交AD、BC于E、F, 则图中的全等三角形共有( )
A.1对 B.2对 C.3对 D.4对
7. 如图,△ABC≌△DEF,求证:AD=BE.
8.如图,CD⊥AB,BE⊥AC,垂足分别为D、E,BE交CD于F,且AD=DF,求证:AC= BF.
9. 如图,已知:AC和BD相交于点O,OA=OC,OB=OD,AB与DC平行吗?
说明理由。
10、如图:已知AB=AE,BC=ED,∠B=∠E,AF⊥CD,F为垂足,
求证: ① AC=AD; ②CF=DF。
11、如图,已知∠A=90°,AB=BD,ED⊥BC于D,在图中找出另外一对相等的线段吗?为什么?
12、.在△ABC中,,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E(1)当直线MN绕点C旋转到图①的位置时,求证:DE=AD+BE
(2)当直线MN绕点C旋转到图②的位置时,求证:DE=AD-BE
(3)当直线MN绕点C旋转到图③的位置时,试问:DE、AD、BE有怎样的等量关系 请写出这个等量关系,并加以证明
A
B
C
D
O
4
