高中物理鲁科版必修第一册课件: 连接体、加速度的瞬时性(56 张PPT)
文档属性
| 名称 | 高中物理鲁科版必修第一册课件: 连接体、加速度的瞬时性(56 张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-10-26 09:58:17 | ||
图片预览









文档简介
(共56张PPT)
学法指导课 连接体、加速度的瞬时性
题型一 “并联”连接体问题
互动探究·关键能力
例 如图所示,质量为M、中间为半球形的光滑凹槽放置于光滑水平地面上,
光滑凹槽内有一质量为m的小铁球,现用一水平向右的推力F推动凹槽,小铁
球与光滑凹槽相对静止时,凹槽球心和小铁球的连线与竖直方向成α角。则
下列说法正确的是 ( )
A.小铁球受到的合外力方向水平向左
B.F=(M+m)g tan α
B
C.系统的加速度为g sin α
D.F=Mg tan α
解析 隔离小铁球受力分析,得F合=mg tan α=ma,且合外力方向水平向右,
故小铁球的加速度为g tan α,因为小铁球与凹槽相对静止,故系统的加速度也
为g tan α,A、C错误;对整体受力分析,得F=(M+m)a=(M+m)·g tan α,故B正确,D
错误。
学法指导
对连接体问题,求加速度是解题的切入点,灵活应用整体法和隔离法是解题的
关键,一般解题思路是:
(1)当整体的外力已知时,先整体求加速度,再隔离求内力。
(2)当整体的外力未知时,先隔离求加速度,再整体分析求解。
(3)当整体或隔离都不能直接求解时,应通过联立方程组求解。
迁移应用
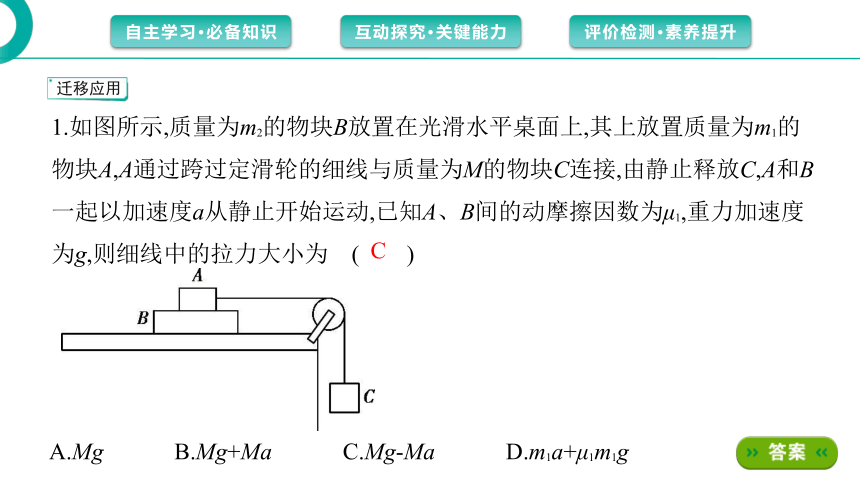
1.如图所示,质量为m2的物块B放置在光滑水平桌面上,其上放置质量为m1的
物块A,A通过跨过定滑轮的细线与质量为M的物块C连接,由静止释放C,A和B
一起以加速度a从静止开始运动,已知A、B间的动摩擦因数为μ1,重力加速度
为g,则细线中的拉力大小为 ( )
A.Mg B.Mg+Ma C.Mg-Ma D.m1a+μ1m1g
C
解析 对物块C,由牛顿第二定律得Mg-FT=Ma,解得FT=Mg-Ma,A、B错误,
C正确;对物块A,由牛顿第二定律得FT-f=m1a,解得FT=m1a+f,因f为静摩擦力,故
不一定等于μ1m1g,D错误。
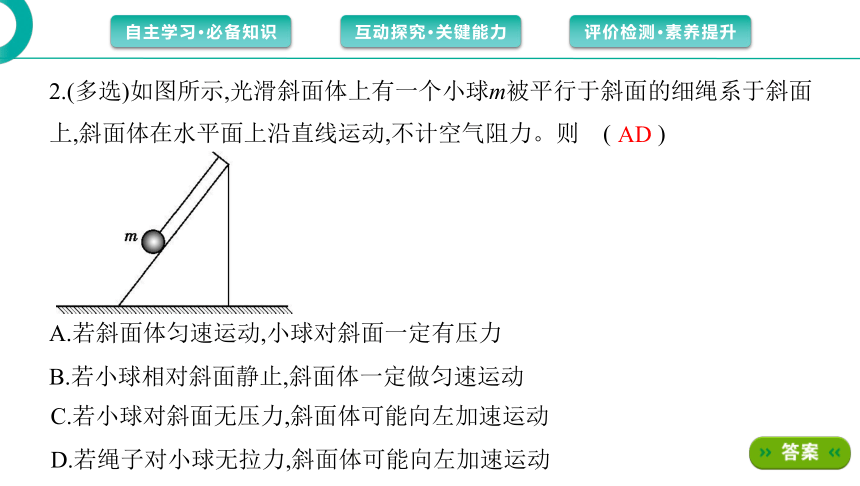
2.(多选)如图所示,光滑斜面体上有一个小球m被平行于斜面的细绳系于斜面
上,斜面体在水平面上沿直线运动,不计空气阻力。则 ( )
A.若斜面体匀速运动,小球对斜面一定有压力
B.若小球相对斜面静止,斜面体一定做匀速运动
C.若小球对斜面无压力,斜面体可能向左加速运动
D.若绳子对小球无拉力,斜面体可能向左加速运动
AD
解析 若斜面体匀速运动,小球也做匀速运动,则小球受力平衡,小球受
重力和绳子的拉力及斜面对小球的支持力,这三个力合力为零,所以小球对斜
面一定有压力,A正确;如果整体向左加速或向右加速过程中,加速度比较小,
小球有可能相对斜面静止,故斜面体不一定匀速运动,B错误;若小球对斜面无
压力,小球只受重力和绳子的拉力,加速度方向水平向右,则斜面体的加速度
也水平向右,可以向右加速,也可以向左减速,C错误;若绳子没有拉力,则小球
只受重力和支持力,加速度方向水平向左,则斜面体的加速度也水平向左,可
以向左加速,也可以向右减速,D正确。
题型二 “串联”连接体问题
例 如图所示,质量为m1、m2的两物块处于光滑水平面上,中间由轻绳相连,
一个恒力F作用在物块上,一起向右做匀加速运动。
(1)此时绳上的拉力T是多少
(2)如果地面粗糙且动摩擦因数为μ,绳上的拉力T是多少
答案 见解析
解析 (1)对整体有F=(m1+m2)a
对质量为m2的物块有T=m2a
解得T= F
(2)对整体:F-μ(m1+m2)g=(m1+m2)a
对质量为m2的物块有T-μm2g=m2a
联立解得T= F
学法指导
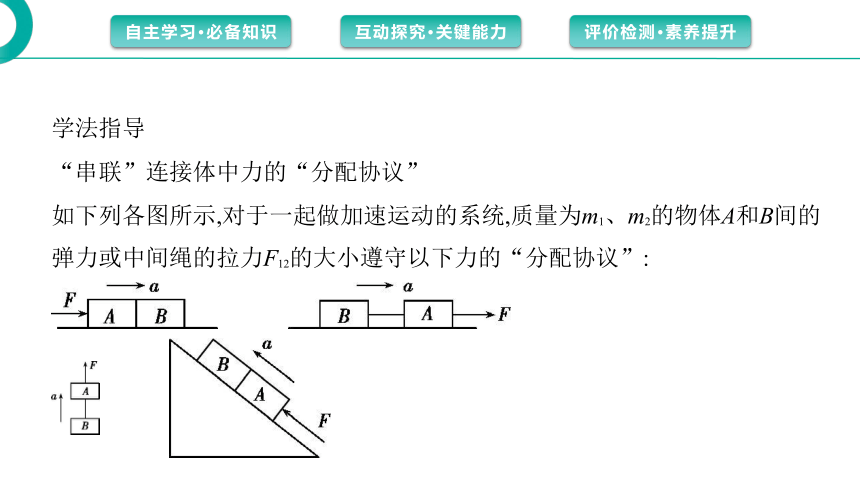
“串联”连接体中力的“分配协议”
如下列各图所示,对于一起做加速运动的系统,质量为m1、m2的物体A和B间的
弹力或中间绳的拉力F12的大小遵守以下力的“分配协议”:
(1)若外力F作用于A上,则F12= 。
(2)若外力F作用于B上,则F12= 。
注意:①此“分配协议”与有无摩擦无关(若有摩擦,两物体与接触面间的动
摩擦因数必须相同);
②两物体间若有连接物,连接物的质量必须很小,可忽略(如轻绳、轻杆、轻
弹簧等);
③物体系统在水平面、斜面或竖直方向上一起加速运动时,此“分配协议”
成立。
迁移应用
1.如图所示,物块A、B质量相等,在水平恒力F的作用下,在水平面上做匀加速
直线运动,若水平面光滑,物块A的加速度大小为a1,物块A、B间的相互作用力
大小为FN1;若水平面粗糙,且物块A、B与水平面间的动摩擦因数μ相同,物块B
的加速度大小为a2,物块A、B间的相互作用力大小为FN2,则以下判断正确的
是 ( )
A.a1=a2 B.FN1=F C.FN1=FN2 D.FN1C
解析 设物块A、B的质量均为m,接触面光滑时,对A、B组成的整体分析,
根据牛顿第二定律得a1= ,对物块B分析,由牛顿第二定律得FN1=ma1= ;接
触面粗糙时,对A、B组成的整体分析,根据牛顿第二定律得a2= =
-μg,可知a1>a2,对物块B分析,由牛顿第二定律得FN2-μmg=ma2,解得FN2= ,则FN1
=FN2,C正确,A、B、D错误。
2.如图所示,A、B两物体用细绳连接后放在斜面上,斜面倾角为α,如果两物体
与斜面间的动摩擦因数都为μ,则在它们下滑过程中(重力加速度为g) ( )
A.它们的加速度a=g sin α
B.它们的加速度a>g sin α
C.细绳中的张力FT=0
D.细绳中的张力FT=mAg(sin α-cos α)
C
解析 对A、B组成的系统运用牛顿第二定律有(mA+mB)g sin α-μ(mA+mB)g
cos α=(mA+mB)a,解得a=(sin α-μ cos α)g牛顿第二定律有mAg sin α-μmAg cos α-FT=mAa,解得FT=0,C正确,D错误。
例 如图所示,小球A、B的质量分别是m和2m,用轻质弹簧相连,然后用细绳
悬挂并保持静止状态,则在剪断细绳的瞬间,A、B的加速度分别是(重力加速
度为g) ( )
A.aA=0,aB=0 B.aA=3g,aB=0
C.aA=g,aB=2g D.aA=0,aB=3g
题型三 瞬时加速度问题
B
解析 在没有剪断细绳前,A、B都静止,加速度都为零,分别对A、B进行
受力分析,如图甲、乙所示,对B有F弹=2mg,对A有FT=mg+F弹'=3mg。当剪断细
绳瞬间,弹簧形变来不及恢复,即F弹、F弹'不变,而FT立即消失,则A受力分析如
图丙所示,F合=mg+F弹'=maA,即aA=3g,B受力不变,合力为零,加速度为零。
学法指导
1.两种模型
(1)细线(或接触面):形变量极小,形变恢复不需要时间,弹力在瞬时可以完成
突变。
(2)弹簧(或橡皮绳):形变量大,形变恢复需要时间,弹力在瞬间不变,但需要注
意,如果弹簧发生断折或将一端物体突然移除,则弹力瞬间消失。
2.求瞬时加速度思路
分析瞬时变化前后
物体的受力情况 列牛顿第二
定律方程 求瞬时
加速度
迁移应用
1.如图所示,天花板上固定有一光滑的定滑轮,绕过定滑轮且不可伸长的轻质
细绳左端悬挂一质量为M的铁块,右端悬挂有两个质量均为m的铜块,上下两
铜块用轻质细线连接,中间夹一轻质弹簧处于压缩状态,此时细线上的张力为
2mg,最初系统处于静止状态,某瞬间将细线烧断,则左端铁块的加速度大小为
(重力加速度为g) ( )
A. g B. g
C. g D. g
C
解析 根据题意,烧断细线前细绳上的张力为2mg,可得到M=2m,以右面
下端的铜块为研究对象,根据平衡条件可知,细线烧断前弹簧的弹力为mg,细
线烧断的瞬间,铁块与右端上面的铜块间细绳的张力也会发生变化,但二者加
速度大小相同,根据牛顿第二定律,有2mg+mg-mg=3ma,解得a= g,故C项正
确。
2.如图所示,竖直放置在水平面上的轻质弹簧上放着质量为2 kg的物体A,A处
于静止状态。若将一个质量为3 kg的物体B竖直向下轻放在A上的一瞬间,则
B对A的压力大小为(g取10 m/s2) ( )
A.30 N B.0
C.15 N D.12 N
D
解析 开始时弹簧的弹力等于A的重力,即F=mAg,放上B的瞬间,弹簧弹力
不变,对整体分析,根据牛顿第二定律得a= = = m/s2=
6 m/s2,对B隔离分析,有mBg-FN=mBa,则FN=mB(g-a)=3×(10-6) N=12 N,故D项正
确,A、B、C三项错误。
基础达标练
1.(2021浙江温州高一期末)用一水平恒力F推着A和B两物体,沿光滑水平地面
一起向右做匀加速直线运动,则下列说法正确的是 ( )
A.A对B的作用力大小等于F
B.A对B的作用力大小一定等于
C.若A的质量越大,则A对B的作用力一定越大
D.若B的质量越大,则A对B的作用力一定越大
D
解析 以A、B整体为研究对象,根据牛顿第二定律可得F=(mA+mB)a,解得a=
,再以B为研究对象,根据牛顿第二定律可得A对B的作用力N=mBa=
= ,由于A、B的质量关系未知,故无法判断A对B的作用力大小,但
B的质量越大,则A对B的作用力一定越大。
2.(2021河南新乡高一期末)如图所示,两个质量均为m的物体A、B叠放在水平
地面上,已知A与B间的动摩擦因数为μ1,B与地面间的动摩擦因数为μ2(μ1>μ2),
现对A施加一水平向右的变力F(F>0),若某时刻使A、B一起向右做匀减速直
线运动,重力加速度大小为g,则此时A受到的摩擦力 ( )
A.大于(μ1+μ2)mg B.等于(μ1+μ2)mg
C.等于2μ2mg D.小于2μ2mg
D
解析 两物体一起向右做减速运动,则加速度向左,对物体A受到向右的力F,
对物体B,由牛顿第二定律2μ2mg-fAB=ma,解得fAB=2μ2mg-ma<2μ2mg,故选D。
3.如图所示,粗糙水平面上放置B、C两物体,A叠放在C上,A、B、C的质量分
别为m、2m和3m,物体B、C与水平面间的动摩擦因数相同,其间用一不可伸
长的轻绳相连,轻绳能承受的最大拉力为FT。现用水平拉力F拉物体B,使三
个物体以同一加速度向右运动,则 ( )
A.此过程中物体C受五个力作用
B.当F逐渐增大到FT时,轻绳刚好被拉断
C.当F逐渐增大到1.5FT时,轻绳刚好被拉断
C
D.若水平面光滑,则轻绳刚断时,A、C间的摩擦力为
解析 对物体A受力分析,A受重力、支持力和向右的静摩擦力,由此可知C受
重力、A对C的压力、地面的支持力、绳子的拉力、A对C的摩擦力以及地面
的摩擦力这6个作用力,故A错误;对整体分析,整体的加速度a= =
-μg,运用隔离法对A、C分析,根据牛顿第二定律得FT-μ·4mg=4ma,计算得出FT
= F。当F=1.5FT时,轻绳刚好被拉断,故B错误,C正确;若水平面光滑,轻绳刚
断时,对A、C分析,加速度a= ,运用隔离法对A分析,A受到的摩擦力Ff=ma=
,故D错误。
4.(2021重庆南开中学高一期末)如图所示,质量分别为2m、3m的A、B两个小
物块叠放在一起,从水平地面上以相同的初速度v0竖直上抛,它们受到的空气
阻力大小均恒为F0,下列说法正确的是 ( )
A.在上升过程中A的加速度小于B的加速度
B.A上升的最大高度小于B上升的最大高度
D
C.在下降过程中A与B间的弹力大小为 F0
D.B下降过程所用的时间小于A下降过程所用的时间
解析 上升过程中A、B两个小物块一起向上做减速运动,则它们有共同的加
速度,上升的最大高度一样,所以A、B错误;下降过程中,A、B两个小物块分
开下降,由牛顿第二定律有2mg-F0=2maA,3mg-F0=3maB,解得aA=g- , aB=g- ,
由于aB>aA,所以B下降的比A快,则B下降过程所用的时间小于A下降过程所用
的时间,所以D正确,C错误。
5.(2021江苏南通高一期末)如图所示,质量分别为m1=2 kg、m2=4 kg的A、B两
物体置于光滑的水平面上,中间用轻质弹簧测力计连接,大小均为10 N的水平
拉力F1、F2分别作用在A、B上,系统处于静止状态。下列说法正确的是 ( )
A.弹簧测力计的示数是0
B.弹簧测力计的示数是20 N
C.撤去F2的瞬间,B的加速度大小为2.5 m/s2
D.撤去F1的瞬间,B的加速度大小为2.5 m/s2
C
解析 对B物体分析,由平衡条件可得弹簧测力计的拉力F等于F2,所以弹簧测
力计的示数是10 N,所以A、B错误;撤去F2的瞬间,弹簧测力计的拉力F不发
生变化,所以由牛顿第二定律有,B物体的加速度大小为a2= = m/s2=2.5 m/
s2,C正确;撤去F1的瞬间,弹簧测力计的拉力F不发生变化,所以B物体的合外力
不变,加速度大小为0,D错误。
6.(2021湖北荆州高一期末)如图所示,小球一端用水平轻弹簧系住,另一端用
与竖直方向成θ=30°的轻质细线连接,恰好处于静止状态。细线被烧断的瞬
间,小球的加速度大小为(已知重力加速度大小为g=10 m/s2) ( )
A.5 m/s2 B.10 m/s2
C. m/s2 D. m/s2
D
解析 小球恰好处于静止状态时,由平衡条件得细线拉力为T= ,弹簧的弹
力为F=mg tan θ,细线被烧断的瞬间,弹簧弹力不变,所以重力与弹力的合力大
小等于细线开始时的拉力,由牛顿第二定律有F合=T= =ma,解得小球的加
速度大小为a= m/s2,所以D正确。
7.如图所示,质量为M的小车放在光滑的水平面上,小车上用细线悬吊一质量
为m的小球,M>m,用一力F水平向右拉小球,使小球和车一起以加速度a向右运
动时,细线与竖直方向成θ角,细线的拉力为F1。若用一力F'水平向左拉小车,
使小球和其一起以加速度a'向左运动时,细线与竖直方向也成θ角,细线的拉
力为F1'。则 ( )
A.a'=a,F1'=F1 B.a'>a,F1'=F1
C.a'a,F1'>F1
B
解析 当用力F水平向右拉小球时,以小球为研究对象,竖直方向有F1 cos θ=
mg,水平方向有F-F1 sin θ=ma,以整体为研究对象有F=(m+M)a,解得a= g tan
θ;当用力F'水平向左拉小车时,以球为研究对象,竖直方向有F1' cos θ=mg,水平
方向有F1' sin θ=ma',解得a'=g tan θ,结合两种情况,有F1=F1',结合M>m有a'>a。
故选B。
8.(多选)(2021山东枣庄高一期末)趣味运动会上,运动员手持网球拍托球沿水
平面匀加速跑步。设球拍和球质量分别为M、m,球拍平面和水平面之间的
夹角为θ,球拍与球保持相对静止,它们之间的摩擦力及空气阻力不计。重力
加速度大小为g。下列判断正确的是 ( )
A.运动员的加速度大小为g tan θ
B.球拍对球的作用力大小为mg
AC
C.运动员对球拍的作用力大小为
D.若运动员的加速度大于g sin θ,球一定沿球拍向上运动
解析 AC 对球进行受力分析如图甲所示,根据牛顿第二定律可得N sin θ=
ma,N cos θ=mg,解得a=g tan θ,N= ,A正确,B错误;以球拍和球整体为研究
对象,受力分析如图乙所示,根据牛顿第二定律可得,运动员对球拍的作用力
大小为F= ,故C正确;当a>g tan θ时,球将向上运动,但由于g tan θ与a
的大小关系未知,故球不一定沿球拍向上运动,故D错误。
甲
乙
素养提升练
9.(多选)如图所示,足够长的水平桌面上放置着质量为m、长度为L的长木
板B,质量也为m的物体A放置在长木板B的右端,轻绳1的一端与A相连,另一端
跨过轻质定滑轮与B相连,在长木板的右侧用跨过定滑轮的轻绳2系着质量为
2m的物体C。已知重力加速度为g,各接触面之间的动摩擦因数为μ(μ<0.5),不
计绳与滑轮间的摩擦,忽略空气阻力,系统由静止开始运动,下列说法正确的
是 ( )
BD
A.A、B、C的加速度大小均为
B.轻绳1的拉力为
C.轻绳2的拉力为mg
D.当A运动到B的左端时,物体C的速度大小为
解析 BD 三个物体的加速度大小相等,设加速度大小均为a,对物体A,T1-μ
mg=ma,对B,T2-μmg-2μmg-T1=ma,对C,2mg-T2=2ma,联立解得a= g-μg,T1= mg,
T2=mg+2μmg,B正确,A、C错误;A运动到B的左端时有 at2+ at2=L,此
时A、B、C的速度大小均为v=at= ,D正确。
10.(多选)水平地面上固定一足够长的光滑斜面,斜面倾角θ=30°,如图所示。
斜面上有一楔形物体A,A的上表面水平,A上放一物块B,已知B的质量为m,A、
B间动摩擦因数为μ(μ> ),重力加速度为g。现对A施加一水平推力,使A、B一
起运动,下列说法正确的是 ( )
ACD
A.若A、B一起沿斜面向上做匀速运动,则B受到A的支持力等于mg
B.若A、B一起沿斜面向上做匀速运动,则B受到A的摩擦力等于 mg
C.若A、B一起沿斜面向上以 g的加速度做匀加速运动,则B受到A的支持力
等于 mg
D.若A、B一起沿斜面向上以 g的加速度做匀加速运动,则B受到A的摩擦力
等于 mg
解析 ACD 若A、B一起沿斜面向上匀速运动时,对B进行受力分析可知,B
处于平衡状态,B受到A的支持力等于mg,B与A之间没有摩擦力,A正确,B错误;
若A、B一起沿斜面向上以 g的加速度做匀加速运动,对B进行受力分析,在竖
直方向上FN-mg=ma sin θ,可得B受到A的支持力FN= mg,水平方向上,B受到A
的摩擦力f=ma cos θ= mg,C、D正确。
11.(2021安徽滁州高一期末)如图所示,在水平桌面的边角处有一轻质光滑的
定滑轮K,一条不可伸长的轻绳绕过定滑轮K分别与物体A、B相连,A、B的质
量分别为mA=4 kg、mB=2 kg。现用一水平恒力F拉物体A,使物体B上升(A、B
均从静止开始运动)。已知当B上升距离h=0.2 m时,B的速度为v=2 m/s。已知
A与桌面间的动摩擦因数μ=0.25,重力加速度为g=10 m/s2。求:
(1)A、B系统的加速度大小;
(2)力F的大小和物体B对轻绳的拉力;
(3)若当B的速度为v=2 m/s时,外界原因导致轻绳突然断了,那么在B上升的过
程中,A向左运动多远
答案 (1)10 m/s2 (2)90 N 40 N,方向竖直向下 (3)0.8 m
解析 (1)物体B匀加速上升时,根据速度位移公式,有v2=2ah
解得a=10 m/s2
(2)对A运用牛顿第二定律,得到
F-μmAg-T=mAa
对B运用牛顿第二定律,得到
T-mBg=mBa
联立解得F=90 N,T=40 N
根据牛顿第三定律,物体B对轻绳的拉力大小为40 N,方向竖直向下
(3)轻绳断开后,B物体由于惯性继续上升,根据速度时间公式,有
t= =0.2 s
对A运用牛顿第二定律,得到
F-μmAg=mAa',a'=20 m/s2
物体A做匀加速直线运动,根据位移时间公式,有
x=vt+ a't2
解得x=0.8 m
创新拓展练
12.(2021山东烟台高一期末)如图所示,在固定的水平光滑杆上穿一个质量为
m的小球A,一劲度系数为k的轻质弹簧一端固定在竖直墙面上的O点,另一端
与球A拴接。用两条等长的细绳将质量为2m的小球B分别与A、O相连,两条
细绳之间的夹角为θ,球A、B保持静止状态。已知重力加速度为g。求:
(1)A、B之间细绳所受拉力大小;
(2)水平杆对球A的弹力大小和弹簧的压缩量;
(3)若剪断A、B之间细绳,则剪断绳瞬间球B的加速度大小。
答案 (1) (2)2mg
(3)g sin
解析 (1)对B球受力分析如图甲所示
甲
设A、B之间细绳所受拉力为F1,由平衡条件
2F1 cos =2mg
可得F1=
(2)对A球受力分析如图乙所示
乙
由平衡条件F2=F1' sin ,F3=F1' cos +mg,F1'=F1可得水平杆对球A的弹力大小
F3=2mg
由胡克定律F2=kΔx可得
弹簧的压缩量Δx=
(3)若剪断A、B之间细绳,球B的加速度方向沿着以O为圆心、OB为半径的圆
弧切线方向,垂直细绳方向的分力F=2mg sin
由牛顿第二定律得
a= = =g sin
解题思路 先以B为研究对象可求出绳上的拉力,再以A为研究对象,由平衡
条件可求弹簧的弹力;注意细绳上的力可以突变,而弹簧的弹力只要形变在,
则对应的弹力就在。
解题感悟 本题考查连接体的基本处理方法,要求学生能熟练掌握整体法和
隔离法在求解不同问题时的选择,还考查了瞬时加速度的问题,弹簧的弹力和
绳上弹力的突变情况。
学法指导课 连接体、加速度的瞬时性
题型一 “并联”连接体问题
互动探究·关键能力
例 如图所示,质量为M、中间为半球形的光滑凹槽放置于光滑水平地面上,
光滑凹槽内有一质量为m的小铁球,现用一水平向右的推力F推动凹槽,小铁
球与光滑凹槽相对静止时,凹槽球心和小铁球的连线与竖直方向成α角。则
下列说法正确的是 ( )
A.小铁球受到的合外力方向水平向左
B.F=(M+m)g tan α
B
C.系统的加速度为g sin α
D.F=Mg tan α
解析 隔离小铁球受力分析,得F合=mg tan α=ma,且合外力方向水平向右,
故小铁球的加速度为g tan α,因为小铁球与凹槽相对静止,故系统的加速度也
为g tan α,A、C错误;对整体受力分析,得F=(M+m)a=(M+m)·g tan α,故B正确,D
错误。
学法指导
对连接体问题,求加速度是解题的切入点,灵活应用整体法和隔离法是解题的
关键,一般解题思路是:
(1)当整体的外力已知时,先整体求加速度,再隔离求内力。
(2)当整体的外力未知时,先隔离求加速度,再整体分析求解。
(3)当整体或隔离都不能直接求解时,应通过联立方程组求解。
迁移应用
1.如图所示,质量为m2的物块B放置在光滑水平桌面上,其上放置质量为m1的
物块A,A通过跨过定滑轮的细线与质量为M的物块C连接,由静止释放C,A和B
一起以加速度a从静止开始运动,已知A、B间的动摩擦因数为μ1,重力加速度
为g,则细线中的拉力大小为 ( )
A.Mg B.Mg+Ma C.Mg-Ma D.m1a+μ1m1g
C
解析 对物块C,由牛顿第二定律得Mg-FT=Ma,解得FT=Mg-Ma,A、B错误,
C正确;对物块A,由牛顿第二定律得FT-f=m1a,解得FT=m1a+f,因f为静摩擦力,故
不一定等于μ1m1g,D错误。
2.(多选)如图所示,光滑斜面体上有一个小球m被平行于斜面的细绳系于斜面
上,斜面体在水平面上沿直线运动,不计空气阻力。则 ( )
A.若斜面体匀速运动,小球对斜面一定有压力
B.若小球相对斜面静止,斜面体一定做匀速运动
C.若小球对斜面无压力,斜面体可能向左加速运动
D.若绳子对小球无拉力,斜面体可能向左加速运动
AD
解析 若斜面体匀速运动,小球也做匀速运动,则小球受力平衡,小球受
重力和绳子的拉力及斜面对小球的支持力,这三个力合力为零,所以小球对斜
面一定有压力,A正确;如果整体向左加速或向右加速过程中,加速度比较小,
小球有可能相对斜面静止,故斜面体不一定匀速运动,B错误;若小球对斜面无
压力,小球只受重力和绳子的拉力,加速度方向水平向右,则斜面体的加速度
也水平向右,可以向右加速,也可以向左减速,C错误;若绳子没有拉力,则小球
只受重力和支持力,加速度方向水平向左,则斜面体的加速度也水平向左,可
以向左加速,也可以向右减速,D正确。
题型二 “串联”连接体问题
例 如图所示,质量为m1、m2的两物块处于光滑水平面上,中间由轻绳相连,
一个恒力F作用在物块上,一起向右做匀加速运动。
(1)此时绳上的拉力T是多少
(2)如果地面粗糙且动摩擦因数为μ,绳上的拉力T是多少
答案 见解析
解析 (1)对整体有F=(m1+m2)a
对质量为m2的物块有T=m2a
解得T= F
(2)对整体:F-μ(m1+m2)g=(m1+m2)a
对质量为m2的物块有T-μm2g=m2a
联立解得T= F
学法指导
“串联”连接体中力的“分配协议”
如下列各图所示,对于一起做加速运动的系统,质量为m1、m2的物体A和B间的
弹力或中间绳的拉力F12的大小遵守以下力的“分配协议”:
(1)若外力F作用于A上,则F12= 。
(2)若外力F作用于B上,则F12= 。
注意:①此“分配协议”与有无摩擦无关(若有摩擦,两物体与接触面间的动
摩擦因数必须相同);
②两物体间若有连接物,连接物的质量必须很小,可忽略(如轻绳、轻杆、轻
弹簧等);
③物体系统在水平面、斜面或竖直方向上一起加速运动时,此“分配协议”
成立。
迁移应用
1.如图所示,物块A、B质量相等,在水平恒力F的作用下,在水平面上做匀加速
直线运动,若水平面光滑,物块A的加速度大小为a1,物块A、B间的相互作用力
大小为FN1;若水平面粗糙,且物块A、B与水平面间的动摩擦因数μ相同,物块B
的加速度大小为a2,物块A、B间的相互作用力大小为FN2,则以下判断正确的
是 ( )
A.a1=a2 B.FN1=F C.FN1=FN2 D.FN1
解析 设物块A、B的质量均为m,接触面光滑时,对A、B组成的整体分析,
根据牛顿第二定律得a1= ,对物块B分析,由牛顿第二定律得FN1=ma1= ;接
触面粗糙时,对A、B组成的整体分析,根据牛顿第二定律得a2= =
-μg,可知a1>a2,对物块B分析,由牛顿第二定律得FN2-μmg=ma2,解得FN2= ,则FN1
=FN2,C正确,A、B、D错误。
2.如图所示,A、B两物体用细绳连接后放在斜面上,斜面倾角为α,如果两物体
与斜面间的动摩擦因数都为μ,则在它们下滑过程中(重力加速度为g) ( )
A.它们的加速度a=g sin α
B.它们的加速度a>g sin α
C.细绳中的张力FT=0
D.细绳中的张力FT=mAg(sin α-cos α)
C
解析 对A、B组成的系统运用牛顿第二定律有(mA+mB)g sin α-μ(mA+mB)g
cos α=(mA+mB)a,解得a=(sin α-μ cos α)g
例 如图所示,小球A、B的质量分别是m和2m,用轻质弹簧相连,然后用细绳
悬挂并保持静止状态,则在剪断细绳的瞬间,A、B的加速度分别是(重力加速
度为g) ( )
A.aA=0,aB=0 B.aA=3g,aB=0
C.aA=g,aB=2g D.aA=0,aB=3g
题型三 瞬时加速度问题
B
解析 在没有剪断细绳前,A、B都静止,加速度都为零,分别对A、B进行
受力分析,如图甲、乙所示,对B有F弹=2mg,对A有FT=mg+F弹'=3mg。当剪断细
绳瞬间,弹簧形变来不及恢复,即F弹、F弹'不变,而FT立即消失,则A受力分析如
图丙所示,F合=mg+F弹'=maA,即aA=3g,B受力不变,合力为零,加速度为零。
学法指导
1.两种模型
(1)细线(或接触面):形变量极小,形变恢复不需要时间,弹力在瞬时可以完成
突变。
(2)弹簧(或橡皮绳):形变量大,形变恢复需要时间,弹力在瞬间不变,但需要注
意,如果弹簧发生断折或将一端物体突然移除,则弹力瞬间消失。
2.求瞬时加速度思路
分析瞬时变化前后
物体的受力情况 列牛顿第二
定律方程 求瞬时
加速度
迁移应用
1.如图所示,天花板上固定有一光滑的定滑轮,绕过定滑轮且不可伸长的轻质
细绳左端悬挂一质量为M的铁块,右端悬挂有两个质量均为m的铜块,上下两
铜块用轻质细线连接,中间夹一轻质弹簧处于压缩状态,此时细线上的张力为
2mg,最初系统处于静止状态,某瞬间将细线烧断,则左端铁块的加速度大小为
(重力加速度为g) ( )
A. g B. g
C. g D. g
C
解析 根据题意,烧断细线前细绳上的张力为2mg,可得到M=2m,以右面
下端的铜块为研究对象,根据平衡条件可知,细线烧断前弹簧的弹力为mg,细
线烧断的瞬间,铁块与右端上面的铜块间细绳的张力也会发生变化,但二者加
速度大小相同,根据牛顿第二定律,有2mg+mg-mg=3ma,解得a= g,故C项正
确。
2.如图所示,竖直放置在水平面上的轻质弹簧上放着质量为2 kg的物体A,A处
于静止状态。若将一个质量为3 kg的物体B竖直向下轻放在A上的一瞬间,则
B对A的压力大小为(g取10 m/s2) ( )
A.30 N B.0
C.15 N D.12 N
D
解析 开始时弹簧的弹力等于A的重力,即F=mAg,放上B的瞬间,弹簧弹力
不变,对整体分析,根据牛顿第二定律得a= = = m/s2=
6 m/s2,对B隔离分析,有mBg-FN=mBa,则FN=mB(g-a)=3×(10-6) N=12 N,故D项正
确,A、B、C三项错误。
基础达标练
1.(2021浙江温州高一期末)用一水平恒力F推着A和B两物体,沿光滑水平地面
一起向右做匀加速直线运动,则下列说法正确的是 ( )
A.A对B的作用力大小等于F
B.A对B的作用力大小一定等于
C.若A的质量越大,则A对B的作用力一定越大
D.若B的质量越大,则A对B的作用力一定越大
D
解析 以A、B整体为研究对象,根据牛顿第二定律可得F=(mA+mB)a,解得a=
,再以B为研究对象,根据牛顿第二定律可得A对B的作用力N=mBa=
= ,由于A、B的质量关系未知,故无法判断A对B的作用力大小,但
B的质量越大,则A对B的作用力一定越大。
2.(2021河南新乡高一期末)如图所示,两个质量均为m的物体A、B叠放在水平
地面上,已知A与B间的动摩擦因数为μ1,B与地面间的动摩擦因数为μ2(μ1>μ2),
现对A施加一水平向右的变力F(F>0),若某时刻使A、B一起向右做匀减速直
线运动,重力加速度大小为g,则此时A受到的摩擦力 ( )
A.大于(μ1+μ2)mg B.等于(μ1+μ2)mg
C.等于2μ2mg D.小于2μ2mg
D
解析 两物体一起向右做减速运动,则加速度向左,对物体A受到向右的力F,
对物体B,由牛顿第二定律2μ2mg-fAB=ma,解得fAB=2μ2mg-ma<2μ2mg,故选D。
3.如图所示,粗糙水平面上放置B、C两物体,A叠放在C上,A、B、C的质量分
别为m、2m和3m,物体B、C与水平面间的动摩擦因数相同,其间用一不可伸
长的轻绳相连,轻绳能承受的最大拉力为FT。现用水平拉力F拉物体B,使三
个物体以同一加速度向右运动,则 ( )
A.此过程中物体C受五个力作用
B.当F逐渐增大到FT时,轻绳刚好被拉断
C.当F逐渐增大到1.5FT时,轻绳刚好被拉断
C
D.若水平面光滑,则轻绳刚断时,A、C间的摩擦力为
解析 对物体A受力分析,A受重力、支持力和向右的静摩擦力,由此可知C受
重力、A对C的压力、地面的支持力、绳子的拉力、A对C的摩擦力以及地面
的摩擦力这6个作用力,故A错误;对整体分析,整体的加速度a= =
-μg,运用隔离法对A、C分析,根据牛顿第二定律得FT-μ·4mg=4ma,计算得出FT
= F。当F=1.5FT时,轻绳刚好被拉断,故B错误,C正确;若水平面光滑,轻绳刚
断时,对A、C分析,加速度a= ,运用隔离法对A分析,A受到的摩擦力Ff=ma=
,故D错误。
4.(2021重庆南开中学高一期末)如图所示,质量分别为2m、3m的A、B两个小
物块叠放在一起,从水平地面上以相同的初速度v0竖直上抛,它们受到的空气
阻力大小均恒为F0,下列说法正确的是 ( )
A.在上升过程中A的加速度小于B的加速度
B.A上升的最大高度小于B上升的最大高度
D
C.在下降过程中A与B间的弹力大小为 F0
D.B下降过程所用的时间小于A下降过程所用的时间
解析 上升过程中A、B两个小物块一起向上做减速运动,则它们有共同的加
速度,上升的最大高度一样,所以A、B错误;下降过程中,A、B两个小物块分
开下降,由牛顿第二定律有2mg-F0=2maA,3mg-F0=3maB,解得aA=g- , aB=g- ,
由于aB>aA,所以B下降的比A快,则B下降过程所用的时间小于A下降过程所用
的时间,所以D正确,C错误。
5.(2021江苏南通高一期末)如图所示,质量分别为m1=2 kg、m2=4 kg的A、B两
物体置于光滑的水平面上,中间用轻质弹簧测力计连接,大小均为10 N的水平
拉力F1、F2分别作用在A、B上,系统处于静止状态。下列说法正确的是 ( )
A.弹簧测力计的示数是0
B.弹簧测力计的示数是20 N
C.撤去F2的瞬间,B的加速度大小为2.5 m/s2
D.撤去F1的瞬间,B的加速度大小为2.5 m/s2
C
解析 对B物体分析,由平衡条件可得弹簧测力计的拉力F等于F2,所以弹簧测
力计的示数是10 N,所以A、B错误;撤去F2的瞬间,弹簧测力计的拉力F不发
生变化,所以由牛顿第二定律有,B物体的加速度大小为a2= = m/s2=2.5 m/
s2,C正确;撤去F1的瞬间,弹簧测力计的拉力F不发生变化,所以B物体的合外力
不变,加速度大小为0,D错误。
6.(2021湖北荆州高一期末)如图所示,小球一端用水平轻弹簧系住,另一端用
与竖直方向成θ=30°的轻质细线连接,恰好处于静止状态。细线被烧断的瞬
间,小球的加速度大小为(已知重力加速度大小为g=10 m/s2) ( )
A.5 m/s2 B.10 m/s2
C. m/s2 D. m/s2
D
解析 小球恰好处于静止状态时,由平衡条件得细线拉力为T= ,弹簧的弹
力为F=mg tan θ,细线被烧断的瞬间,弹簧弹力不变,所以重力与弹力的合力大
小等于细线开始时的拉力,由牛顿第二定律有F合=T= =ma,解得小球的加
速度大小为a= m/s2,所以D正确。
7.如图所示,质量为M的小车放在光滑的水平面上,小车上用细线悬吊一质量
为m的小球,M>m,用一力F水平向右拉小球,使小球和车一起以加速度a向右运
动时,细线与竖直方向成θ角,细线的拉力为F1。若用一力F'水平向左拉小车,
使小球和其一起以加速度a'向左运动时,细线与竖直方向也成θ角,细线的拉
力为F1'。则 ( )
A.a'=a,F1'=F1 B.a'>a,F1'=F1
C.a'
B
解析 当用力F水平向右拉小球时,以小球为研究对象,竖直方向有F1 cos θ=
mg,水平方向有F-F1 sin θ=ma,以整体为研究对象有F=(m+M)a,解得a= g tan
θ;当用力F'水平向左拉小车时,以球为研究对象,竖直方向有F1' cos θ=mg,水平
方向有F1' sin θ=ma',解得a'=g tan θ,结合两种情况,有F1=F1',结合M>m有a'>a。
故选B。
8.(多选)(2021山东枣庄高一期末)趣味运动会上,运动员手持网球拍托球沿水
平面匀加速跑步。设球拍和球质量分别为M、m,球拍平面和水平面之间的
夹角为θ,球拍与球保持相对静止,它们之间的摩擦力及空气阻力不计。重力
加速度大小为g。下列判断正确的是 ( )
A.运动员的加速度大小为g tan θ
B.球拍对球的作用力大小为mg
AC
C.运动员对球拍的作用力大小为
D.若运动员的加速度大于g sin θ,球一定沿球拍向上运动
解析 AC 对球进行受力分析如图甲所示,根据牛顿第二定律可得N sin θ=
ma,N cos θ=mg,解得a=g tan θ,N= ,A正确,B错误;以球拍和球整体为研究
对象,受力分析如图乙所示,根据牛顿第二定律可得,运动员对球拍的作用力
大小为F= ,故C正确;当a>g tan θ时,球将向上运动,但由于g tan θ与a
的大小关系未知,故球不一定沿球拍向上运动,故D错误。
甲
乙
素养提升练
9.(多选)如图所示,足够长的水平桌面上放置着质量为m、长度为L的长木
板B,质量也为m的物体A放置在长木板B的右端,轻绳1的一端与A相连,另一端
跨过轻质定滑轮与B相连,在长木板的右侧用跨过定滑轮的轻绳2系着质量为
2m的物体C。已知重力加速度为g,各接触面之间的动摩擦因数为μ(μ<0.5),不
计绳与滑轮间的摩擦,忽略空气阻力,系统由静止开始运动,下列说法正确的
是 ( )
BD
A.A、B、C的加速度大小均为
B.轻绳1的拉力为
C.轻绳2的拉力为mg
D.当A运动到B的左端时,物体C的速度大小为
解析 BD 三个物体的加速度大小相等,设加速度大小均为a,对物体A,T1-μ
mg=ma,对B,T2-μmg-2μmg-T1=ma,对C,2mg-T2=2ma,联立解得a= g-μg,T1= mg,
T2=mg+2μmg,B正确,A、C错误;A运动到B的左端时有 at2+ at2=L,此
时A、B、C的速度大小均为v=at= ,D正确。
10.(多选)水平地面上固定一足够长的光滑斜面,斜面倾角θ=30°,如图所示。
斜面上有一楔形物体A,A的上表面水平,A上放一物块B,已知B的质量为m,A、
B间动摩擦因数为μ(μ> ),重力加速度为g。现对A施加一水平推力,使A、B一
起运动,下列说法正确的是 ( )
ACD
A.若A、B一起沿斜面向上做匀速运动,则B受到A的支持力等于mg
B.若A、B一起沿斜面向上做匀速运动,则B受到A的摩擦力等于 mg
C.若A、B一起沿斜面向上以 g的加速度做匀加速运动,则B受到A的支持力
等于 mg
D.若A、B一起沿斜面向上以 g的加速度做匀加速运动,则B受到A的摩擦力
等于 mg
解析 ACD 若A、B一起沿斜面向上匀速运动时,对B进行受力分析可知,B
处于平衡状态,B受到A的支持力等于mg,B与A之间没有摩擦力,A正确,B错误;
若A、B一起沿斜面向上以 g的加速度做匀加速运动,对B进行受力分析,在竖
直方向上FN-mg=ma sin θ,可得B受到A的支持力FN= mg,水平方向上,B受到A
的摩擦力f=ma cos θ= mg,C、D正确。
11.(2021安徽滁州高一期末)如图所示,在水平桌面的边角处有一轻质光滑的
定滑轮K,一条不可伸长的轻绳绕过定滑轮K分别与物体A、B相连,A、B的质
量分别为mA=4 kg、mB=2 kg。现用一水平恒力F拉物体A,使物体B上升(A、B
均从静止开始运动)。已知当B上升距离h=0.2 m时,B的速度为v=2 m/s。已知
A与桌面间的动摩擦因数μ=0.25,重力加速度为g=10 m/s2。求:
(1)A、B系统的加速度大小;
(2)力F的大小和物体B对轻绳的拉力;
(3)若当B的速度为v=2 m/s时,外界原因导致轻绳突然断了,那么在B上升的过
程中,A向左运动多远
答案 (1)10 m/s2 (2)90 N 40 N,方向竖直向下 (3)0.8 m
解析 (1)物体B匀加速上升时,根据速度位移公式,有v2=2ah
解得a=10 m/s2
(2)对A运用牛顿第二定律,得到
F-μmAg-T=mAa
对B运用牛顿第二定律,得到
T-mBg=mBa
联立解得F=90 N,T=40 N
根据牛顿第三定律,物体B对轻绳的拉力大小为40 N,方向竖直向下
(3)轻绳断开后,B物体由于惯性继续上升,根据速度时间公式,有
t= =0.2 s
对A运用牛顿第二定律,得到
F-μmAg=mAa',a'=20 m/s2
物体A做匀加速直线运动,根据位移时间公式,有
x=vt+ a't2
解得x=0.8 m
创新拓展练
12.(2021山东烟台高一期末)如图所示,在固定的水平光滑杆上穿一个质量为
m的小球A,一劲度系数为k的轻质弹簧一端固定在竖直墙面上的O点,另一端
与球A拴接。用两条等长的细绳将质量为2m的小球B分别与A、O相连,两条
细绳之间的夹角为θ,球A、B保持静止状态。已知重力加速度为g。求:
(1)A、B之间细绳所受拉力大小;
(2)水平杆对球A的弹力大小和弹簧的压缩量;
(3)若剪断A、B之间细绳,则剪断绳瞬间球B的加速度大小。
答案 (1) (2)2mg
(3)g sin
解析 (1)对B球受力分析如图甲所示
甲
设A、B之间细绳所受拉力为F1,由平衡条件
2F1 cos =2mg
可得F1=
(2)对A球受力分析如图乙所示
乙
由平衡条件F2=F1' sin ,F3=F1' cos +mg,F1'=F1可得水平杆对球A的弹力大小
F3=2mg
由胡克定律F2=kΔx可得
弹簧的压缩量Δx=
(3)若剪断A、B之间细绳,球B的加速度方向沿着以O为圆心、OB为半径的圆
弧切线方向,垂直细绳方向的分力F=2mg sin
由牛顿第二定律得
a= = =g sin
解题思路 先以B为研究对象可求出绳上的拉力,再以A为研究对象,由平衡
条件可求弹簧的弹力;注意细绳上的力可以突变,而弹簧的弹力只要形变在,
则对应的弹力就在。
解题感悟 本题考查连接体的基本处理方法,要求学生能熟练掌握整体法和
隔离法在求解不同问题时的选择,还考查了瞬时加速度的问题,弹簧的弹力和
绳上弹力的突变情况。
同课章节目录
- 绪论 撩开物理学的神秘面纱
- 一、源自然之问
- 二、探万物之秘
- 三、采科学之益
- 四、启智慧之迪
- 第1章 运动的描述
- 第1节 空间和时间
- 第2节 质点和位移
- 第3节 速度
- 第4节 加速度
- 第2章 匀变速直线运动
- 第1节 速度变化规律
- 第2节 位移变化规律
- 第3节 实验中的误差和有效数字
- 第4节 科学测量:做直线运动物体的瞬时速度
- 第5节 自由落体运动
- 第3章 相互作用
- 第1节 重力与重心
- 第2节 科学探究:弹力
- 第3节 摩擦力
- 第4章 力与平衡
- 第1节 科学探究:力的合成
- 第2节 力的分解
- 第3节 共点力的平衡
- 第5章 牛顿运动定律
- 第1节 牛顿第一运动定律
- 第2节 科学探究:加速度与力、质量的关系
- 第3节 牛顿第二运动定律
- 第4节 牛顿第三运动定律
- 第5节 超重与失重
