苏教版数学必修1>>第二章函数概念与基本初等函数Ⅰ>>2.2指数函数
文档属性
| 名称 | 苏教版数学必修1>>第二章函数概念与基本初等函数Ⅰ>>2.2指数函数 |

|
|
| 格式 | zip | ||
| 文件大小 | 291.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-08-30 00:00:00 | ||
图片预览





文档简介
(共20张PPT)
2.2
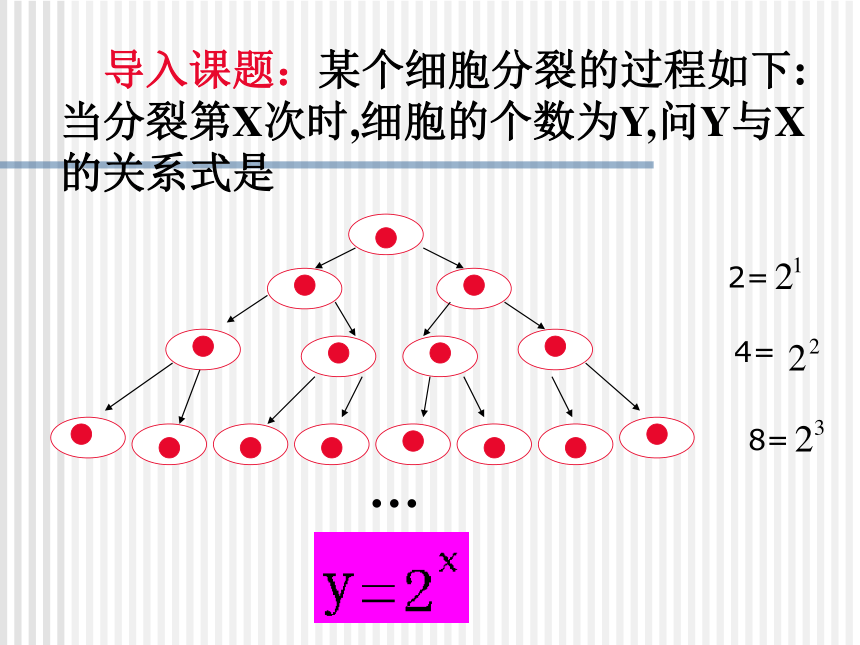
导入课题:某个细胞分裂的过程如下:当分裂第X次时,细胞的个数为Y,问Y与X的关系式是
2=
8=
4=
…
自学教材P54-56
1、什么是指数函数?
2、这个函数的解析式、定义域、值域、单调性、奇偶性是什么?
完成学案上了解新知的部分。
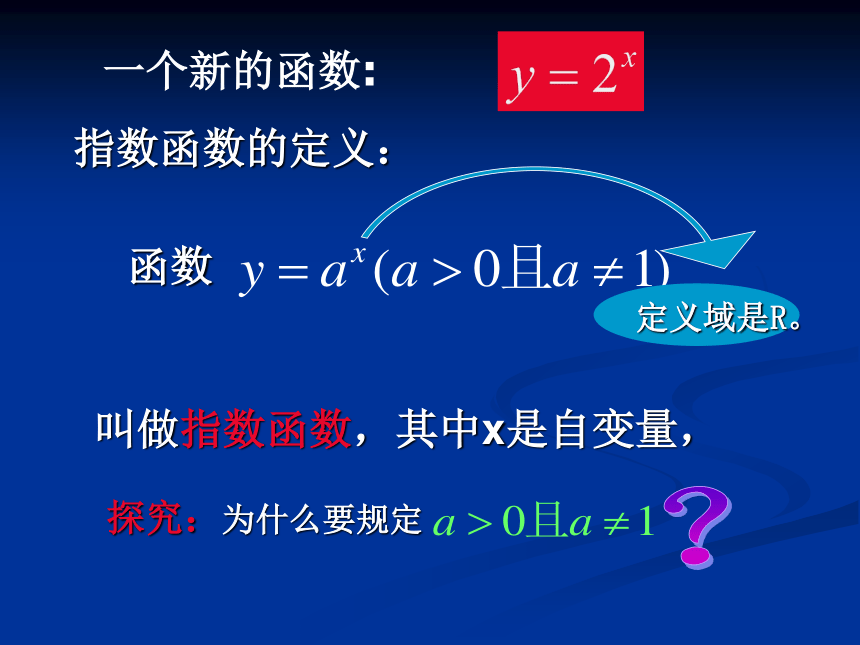
指数函数的定义:
函数
叫做指数函数,其中x是自变量,
定义域是R。
一个新的函数:
探究:为什么要规定
观察指数函数的特点:
系数为1
底数为正数且不为1
自变量仅有这一种形式
例1: 下列函数是否是指数函数
练习:
判断下列函数哪些是指数函数?
不是
是
不是
不是
不是
(1) y=2 x +1 ,(2)y=3×4 X ,
(3) y=3 x , (4) y= ,
(5) y=10 -x ,(6) y=2 x+1 。
不是
例2:判断 是否是一个指数函数,若是指数函数则求a的取值范围.
整体的思想:把2a-1看做一个整体
解:
0
1
1
2
2
x
y
4
3
-1
-2
3
-3
作出函数图像:
1。列表 2。描点 3。连线
y=2x
y= 2- x
图 象
性 质
y
x
0
y=1
(0,1)
y=ax
(a>1)
y
x
(0,1)
y=1
0
y=ax
(0定 义 域 :
值 域 :
必过 点:
在 R 上是
在 R 上是
a>1
0R
( 0 , + ∞ )
( 0 , 1 ) ,即 x = 0 时, y = 1 .
增函数
减函数
指数函数:
y=ax
(a >0且a=1)
图 象
性 质
y
x
0
y=1
(0,1)
y=ax
(a>1)
y
x
(0,1)
y=1
0
y=ax
(0定 义 域 :
值 域 :
必过 点:
在 R 上是
在 R 上是
a>1
0R
( 0 , + ∞ )
( 0 , 1 ) ,即 x = 0 时, y = 1 .
增函数
减函数
当 x < 0 时,0<y < 1;
当 x > 0 时,y > 1.
当 x < 0 时,y > 1;
当 x > 0 时,0<y < 1 。
指数函数:
y=ax
(a >0且a=1)
指数函数图象与性质的应用:
例3 、比较下列各题中两个值的大小:
①
,
x
y
0
1
图象法:底数都为1.7,可以看作
是的两个值
②
,
指数函数图象与性质的应用:
x
y
0
1
③
,
解③ :根据指数函数的性质,得
且
>
从而有
变式训练:1、比较大小
2、比较 的大小,其中a>0且a=1。
例4: 求 下列函数的定义域
?思考探究:这几个函数的值域是什么呢?
2.2
导入课题:某个细胞分裂的过程如下:当分裂第X次时,细胞的个数为Y,问Y与X的关系式是
2=
8=
4=
…
自学教材P54-56
1、什么是指数函数?
2、这个函数的解析式、定义域、值域、单调性、奇偶性是什么?
完成学案上了解新知的部分。
指数函数的定义:
函数
叫做指数函数,其中x是自变量,
定义域是R。
一个新的函数:
探究:为什么要规定
观察指数函数的特点:
系数为1
底数为正数且不为1
自变量仅有这一种形式
例1: 下列函数是否是指数函数
练习:
判断下列函数哪些是指数函数?
不是
是
不是
不是
不是
(1) y=2 x +1 ,(2)y=3×4 X ,
(3) y=3 x , (4) y= ,
(5) y=10 -x ,(6) y=2 x+1 。
不是
例2:判断 是否是一个指数函数,若是指数函数则求a的取值范围.
整体的思想:把2a-1看做一个整体
解:
0
1
1
2
2
x
y
4
3
-1
-2
3
-3
作出函数图像:
1。列表 2。描点 3。连线
y=2x
y= 2- x
图 象
性 质
y
x
0
y=1
(0,1)
y=ax
(a>1)
y
x
(0,1)
y=1
0
y=ax
(0
值 域 :
必过 点:
在 R 上是
在 R 上是
a>1
0
( 0 , + ∞ )
( 0 , 1 ) ,即 x = 0 时, y = 1 .
增函数
减函数
指数函数:
y=ax
(a >0且a=1)
图 象
性 质
y
x
0
y=1
(0,1)
y=ax
(a>1)
y
x
(0,1)
y=1
0
y=ax
(0
值 域 :
必过 点:
在 R 上是
在 R 上是
a>1
0
( 0 , + ∞ )
( 0 , 1 ) ,即 x = 0 时, y = 1 .
增函数
减函数
当 x < 0 时,0<y < 1;
当 x > 0 时,y > 1.
当 x < 0 时,y > 1;
当 x > 0 时,0<y < 1 。
指数函数:
y=ax
(a >0且a=1)
指数函数图象与性质的应用:
例3 、比较下列各题中两个值的大小:
①
,
x
y
0
1
图象法:底数都为1.7,可以看作
是的两个值
②
,
指数函数图象与性质的应用:
x
y
0
1
③
,
解③ :根据指数函数的性质,得
且
>
从而有
变式训练:1、比较大小
2、比较 的大小,其中a>0且a=1。
例4: 求 下列函数的定义域
?思考探究:这几个函数的值域是什么呢?
