数学八年级下苏科版11.1图形与证明

(共14张PPT)
有人说，每人一个苹果，交换一下，每人只还有一个苹果；每人一个思想，交流一下，每人会有两个或多个思想。
图形与证明（一）
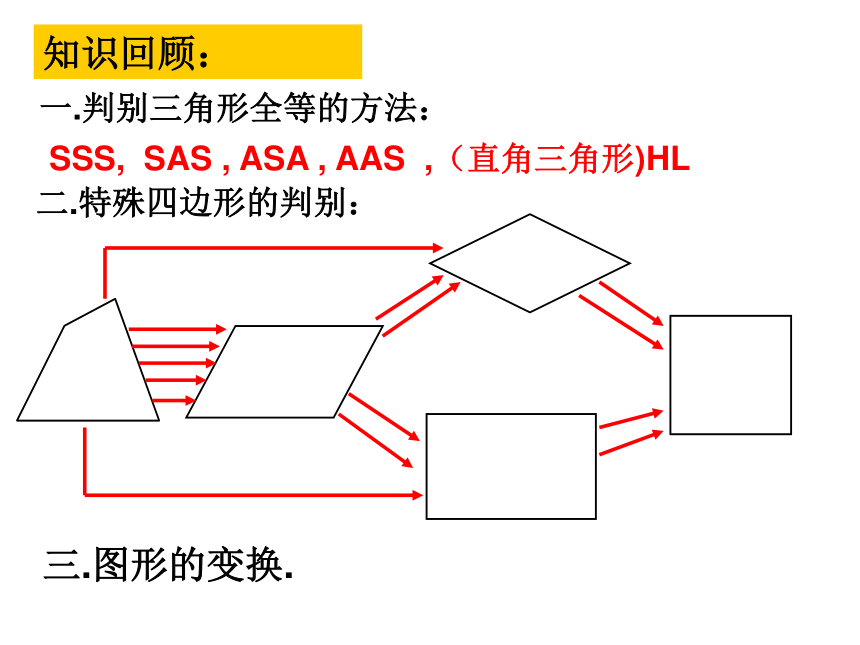
知识回顾：
一.判别三角形全等的方法：
二.特殊四边形的判别：
SSS, SAS , ASA , AAS ,（直角三角形)HL
三.图形的变换.
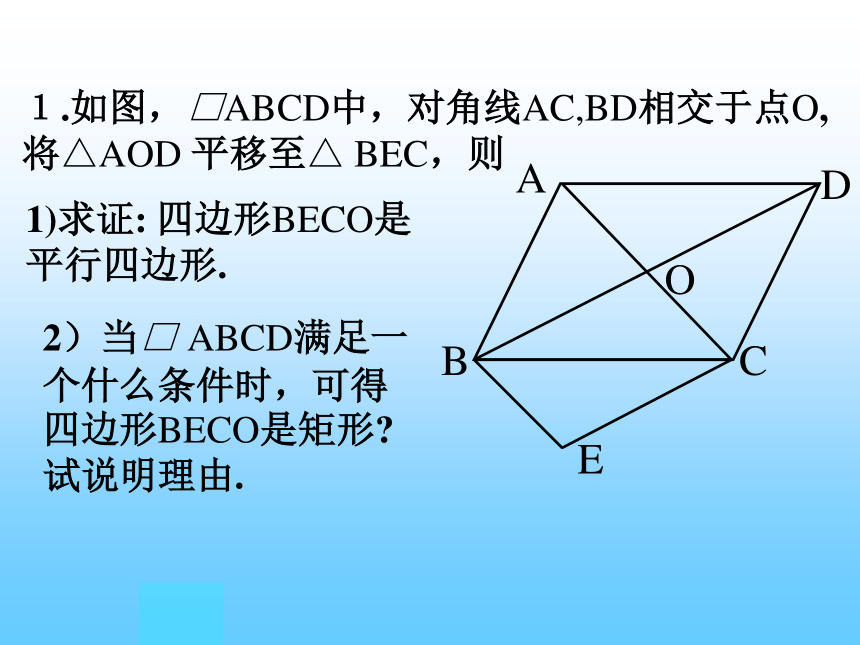
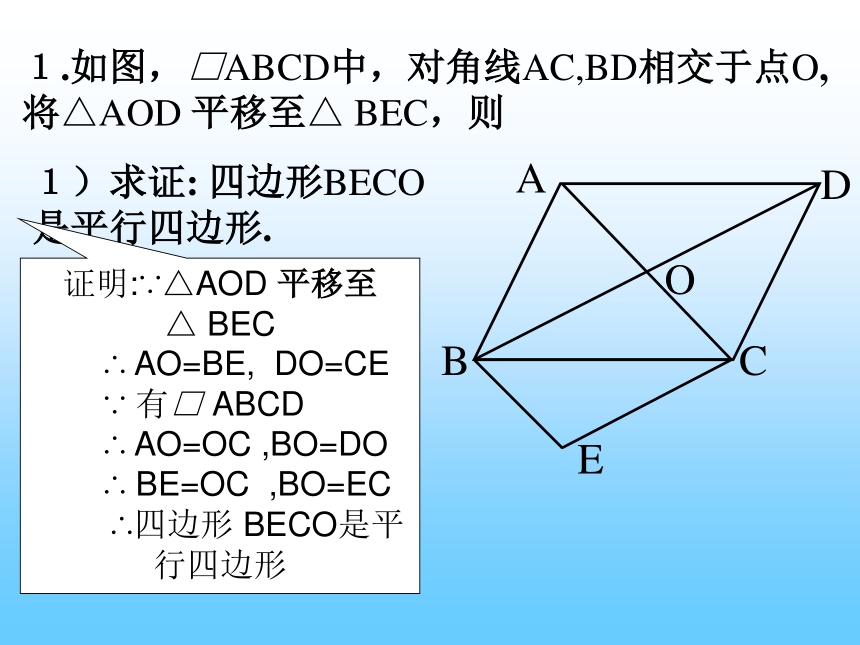
１.如图，□ABCD中，对角线AC,BD相交于点O, 将△AOD 平移至△ BEC，则
1)求证: 四边形BECO是平行四边形.
2）当□ ABCD满足一个什么条件时，可得四边形BECO是矩形 试说明理由.
E
A
O
D
C
B
１.如图，□ABCD中，对角线AC,BD相交于点O, 将△AOD 平移至△ BEC，则
１）求证: 四边形BECO是平行四边形.
2）当□ ABCD满足一个什么条件时，可得四边形BECO是矩形 试说明理由.
E
A
O
D
C
B
证明:∵△AOD 平移至 △ BEC
∴ AO=BE, DO=CE
∵ 有□ ABCD
∴ AO=OC ,BO=DO
∴ BE=OC ,BO=EC
∴四边形 BECO是平行四边形
１.如图，□ABCD中，对角线AC,BD相交于点O, 将△AOD 平移至△ BEC，则
１）求证: 四边形BECO是平行四边形.
2）当□ ABCD满足一个什么条件时，可得四边形BECO是矩形 试说明理由.
E
A
O
D
C
B
证明:∵ △AOD 平移
至△ BEC
∴ AO∥BE,
即 OC ∥ BE
同理可证:BO ∥ EC
∴四边形 BECO是平行四边形
１.如图，□ABCD中，对角线AC,BD相交于点O, 将△AOD 平移至△ BEC，则
2）当□ ABCD满足一个什么条件时，可得四边形BECO是矩形 试说明理由.
E
A
O
D
C
B
１）求证: 四边形BECO是平行四边形.
2、如图:将长方形纸片ABCD沿EF折叠,使C点与A点重合，D点折到D‘点处，则
1）求证:
△AD'E ≌ △ABF
2）四边形AFCE是什么特殊四边形 证明你的结论.
D'
A
B
C
D
E
F
3.如图，已知MN是△ABC的一条中位线,将△AMN以N为旋转中心旋转180°，得到四边形BCEM，则
1) 求证: BM = CE
E
M
N
A
B
C
2)当△ ABC满足一个什么条件时，四边形BCEM为菱形 证明你的结论.
课堂小结:
1.本节课你有哪些收获
2.本节课你在解决开放问题时，怎别如何去思考
1.已知，如图，在梯形ABCD中,AD ∥BC , 将梯形ABCD沿对角线BD折叠，点A恰好落在BC上的A'处。
达标检测：
求证: AB = A'D
2) 判断四边形ABA'D是什么四边形？请证明你的结论。
A
B
A'
C
D
作业：
见学案。
研究2007,2009年中考21小题.
4.已知，如图，等腰梯形ABCD中，P为AB上一动点，E、F、M为DP、CP、DC的中点，
1）试判断四边形PEMF的形状，并证明你的结论.
2）当P在AB上运动到什么位置时，四边形PEMF的形状更特殊 证明你的结论.
C
P
F
E
B
A
D
M