集合的实际应用课件
图片预览


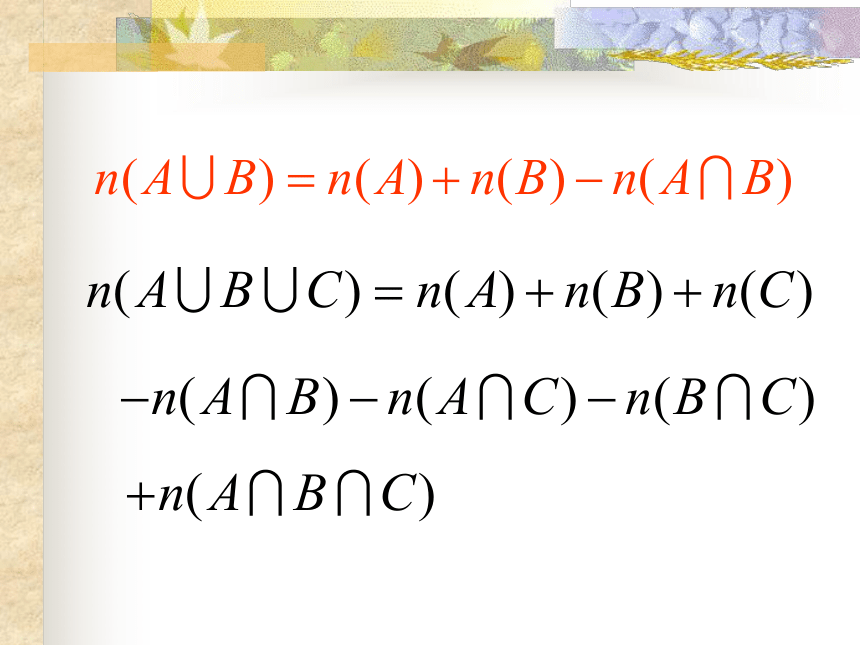



文档简介
(共14张PPT)
基数概念:
设集A是一个有限集,则A里不同元素的个数叫做A的基数,记为n(A)
设A和B是有限集,他们基数分别为n(A),n(B)表示,则由韦恩图可得下面关系:
例1:已知A中含有5个元素,B中含
有6个元素,A∩B中含有3个元素.
A∪B中的元素个数是
8
例2:高一某班的学生中,参加语文
课外小组的有20人,参加数学课外
小组的有22人,既参加语文又参加
数学小组的有10人,既未参加语文
又未参加数学小组的有15人,问该
班共有学生多少人
例3: 50名学生参加跳远和铅球两项测验,跳远和铅球两项及格的人数分别是40人和35人,两项测验均不及格的有5人,求两项测验都及格的有多少人?
例4:某校组织文娱活动,参加音乐组有35人,参加舞蹈有34人,参加戏剧组有29人,其中有12人同时参加音乐组和舞蹈组,有14人同时参加舞蹈组和戏剧组,13人同时参加戏剧组和音乐组,且有5人同时参加三组,问参加文娱活动的人数有多少人?
例5:向50名学生调查对A、B两事件的态度,有如下结果:赞成A的人数是30,其余的不赞成,赞成B的人数是33,其余的不赞成;另外,对A、B都不赞成的学生比对A、B都赞成的学生数的三分之一多1人.问对A、B都赞成的学生和都不赞成的学生各多少人?
分析:
画出韦恩图,形象地表示出各数量关系的联系
解:
方法归纳:
解决这一类问题一般借用数形结合,借助于Venn 图,把抽象的数学语言与直观的图形结合起来
小结:
(1)基本概念的理解与掌握
(2)体会分类讨论,等价转化,
数形结合思想
练习题
1、某区100个外语教师懂英语或俄语,其中懂英语的75人,既懂英语又懂俄语的20人,那么懂俄语的教师为 人.
2、某班共有30名男生,其中20人参加足球队,12人参加蓝球队,10人参加排球队.已知没有一个人同时参加3个队,且每人至少参加一个队,有6人既参加足球队又参加蓝球队,有2人既参加蓝球队又参加排球队,那么既参加足球队又参加排球队的有 人.
练习题
3、在2003年学校召开校运会。设A={x|x是参加100米跑的同学},B={x|x是参加200米跑的同学},C={x|x是参加4×100米接力跑的同学}。学校规定:每个同学最多只能参加两个项目比赛。据统计,高一(8)班共有13人参加了此三项比赛,其中共有8人参加了4×100米接力跑项目,共有6人参加100米跑项目,共有5人参加200米跑项目;同时参加4×100米接力跑和100米跑的同学有3人,同时参加参加4×100米接力跑和200米跑的同学有2人。
问:(Ⅰ)同时参加100米跑和200米跑项目的同学有多少个?
(Ⅱ)只参加200米跑的同学有多少个?
(III)只参加100米跑的同学有多少个?
作 业
教材P20A组T1,5,6
P21B组T3,4,6
基数概念:
设集A是一个有限集,则A里不同元素的个数叫做A的基数,记为n(A)
设A和B是有限集,他们基数分别为n(A),n(B)表示,则由韦恩图可得下面关系:
例1:已知A中含有5个元素,B中含
有6个元素,A∩B中含有3个元素.
A∪B中的元素个数是
8
例2:高一某班的学生中,参加语文
课外小组的有20人,参加数学课外
小组的有22人,既参加语文又参加
数学小组的有10人,既未参加语文
又未参加数学小组的有15人,问该
班共有学生多少人
例3: 50名学生参加跳远和铅球两项测验,跳远和铅球两项及格的人数分别是40人和35人,两项测验均不及格的有5人,求两项测验都及格的有多少人?
例4:某校组织文娱活动,参加音乐组有35人,参加舞蹈有34人,参加戏剧组有29人,其中有12人同时参加音乐组和舞蹈组,有14人同时参加舞蹈组和戏剧组,13人同时参加戏剧组和音乐组,且有5人同时参加三组,问参加文娱活动的人数有多少人?
例5:向50名学生调查对A、B两事件的态度,有如下结果:赞成A的人数是30,其余的不赞成,赞成B的人数是33,其余的不赞成;另外,对A、B都不赞成的学生比对A、B都赞成的学生数的三分之一多1人.问对A、B都赞成的学生和都不赞成的学生各多少人?
分析:
画出韦恩图,形象地表示出各数量关系的联系
解:
方法归纳:
解决这一类问题一般借用数形结合,借助于Venn 图,把抽象的数学语言与直观的图形结合起来
小结:
(1)基本概念的理解与掌握
(2)体会分类讨论,等价转化,
数形结合思想
练习题
1、某区100个外语教师懂英语或俄语,其中懂英语的75人,既懂英语又懂俄语的20人,那么懂俄语的教师为 人.
2、某班共有30名男生,其中20人参加足球队,12人参加蓝球队,10人参加排球队.已知没有一个人同时参加3个队,且每人至少参加一个队,有6人既参加足球队又参加蓝球队,有2人既参加蓝球队又参加排球队,那么既参加足球队又参加排球队的有 人.
练习题
3、在2003年学校召开校运会。设A={x|x是参加100米跑的同学},B={x|x是参加200米跑的同学},C={x|x是参加4×100米接力跑的同学}。学校规定:每个同学最多只能参加两个项目比赛。据统计,高一(8)班共有13人参加了此三项比赛,其中共有8人参加了4×100米接力跑项目,共有6人参加100米跑项目,共有5人参加200米跑项目;同时参加4×100米接力跑和100米跑的同学有3人,同时参加参加4×100米接力跑和200米跑的同学有2人。
问:(Ⅰ)同时参加100米跑和200米跑项目的同学有多少个?
(Ⅱ)只参加200米跑的同学有多少个?
(III)只参加100米跑的同学有多少个?
作 业
教材P20A组T1,5,6
P21B组T3,4,6
