苏科版九年级数学上册 2.1 圆 课件(共23张PPT)
文档属性
| 名称 | 苏科版九年级数学上册 2.1 圆 课件(共23张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 745.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-26 00:00:00 | ||
图片预览


文档简介
(共23张PPT)
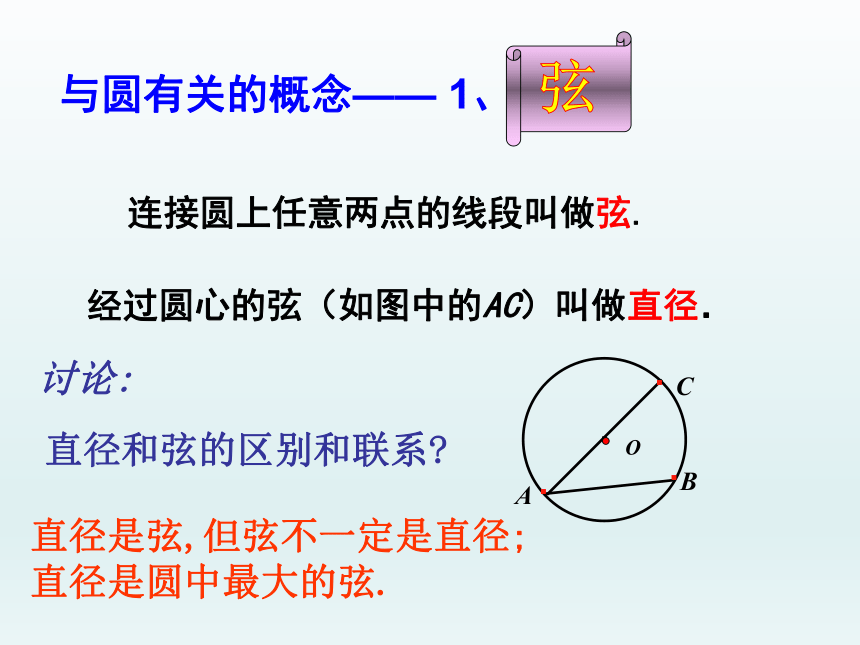
经过圆心的弦(如图中的AC)叫做直径.
·
O
· C
连接圆上任意两点的线段叫做弦.
A ·
·B
与圆有关的概念—— 1、
讨论:
直径和弦的区别和联系
直径是弦,但弦不一定是直径;
直径是圆中最大的弦.
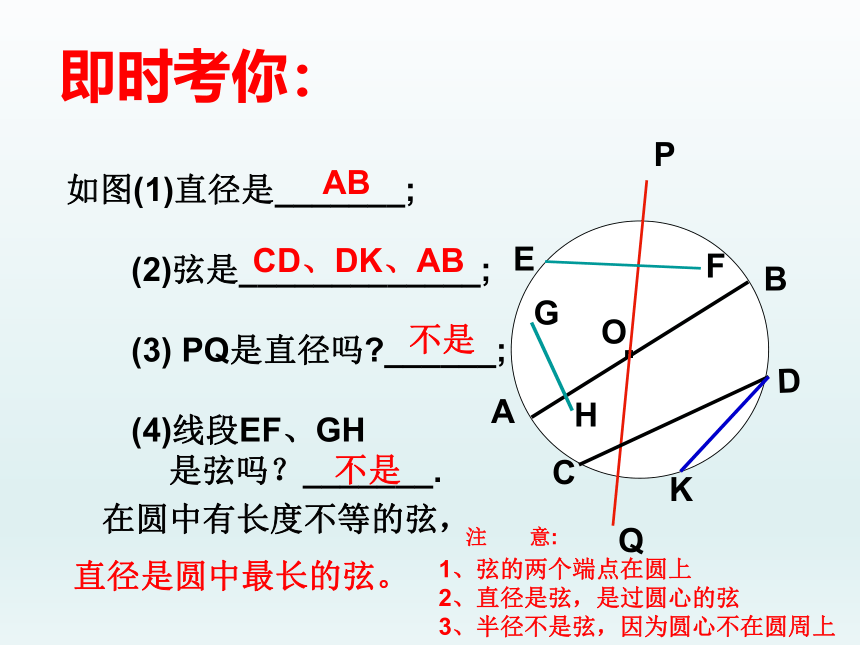
如图(1)直径是_______;
(2)弦是_____________;
(3) PQ是直径吗 ______;
(4)线段EF、GH
是弦吗?_______.
即时考你:
.
O
A
D
Q
C
B
P
H
G
F
E
K
AB
CD、DK、AB
不是
不是
在圆中有长度不等的弦,
直径是圆中最长的弦。
1、弦的两个端点在圆上
2、直径是弦,是过圆心的弦
3、半径不是弦,因为圆心不在圆周上
注 意:
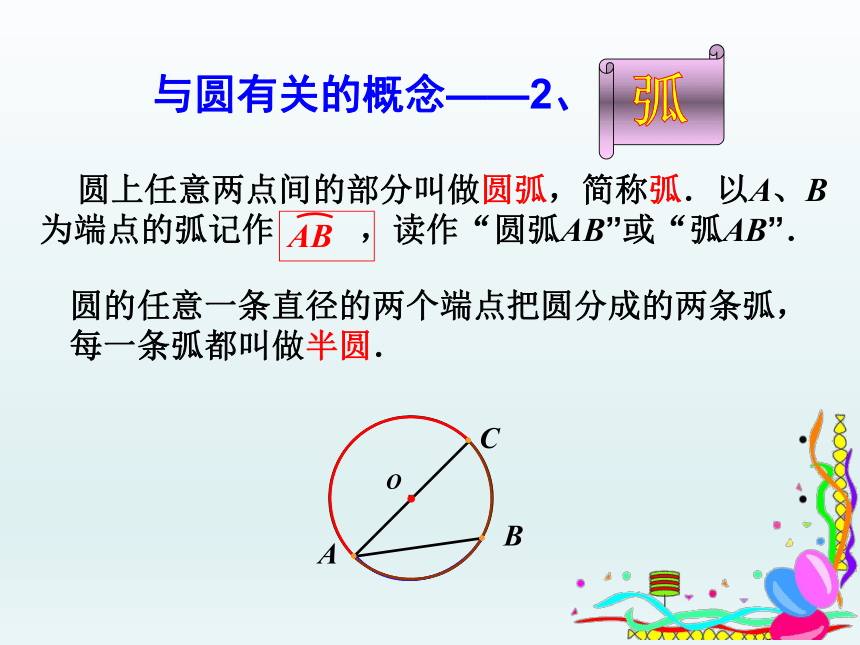
圆的任意一条直径的两个端点把圆分成的两条弧,每一条弧都叫做半圆.
·
O
与圆有关的概念——2、
圆上任意两点间的部分叫做圆弧,简称弧.以A、B为端点的弧记作 ,读作“圆弧AB”或“弧AB”.
AB
A ·
· B
·C
大于半圆的弧有_____________
(用三个字母表示)
·
O
A ·
· B
·C
图中共有____条弧,
其中比半圆小的弧是__________
AB、
BC
ACB、
BAC
6
小于半圆的弧叫做劣弧
大于半圆的弧叫做优弧
与圆有关的概念——
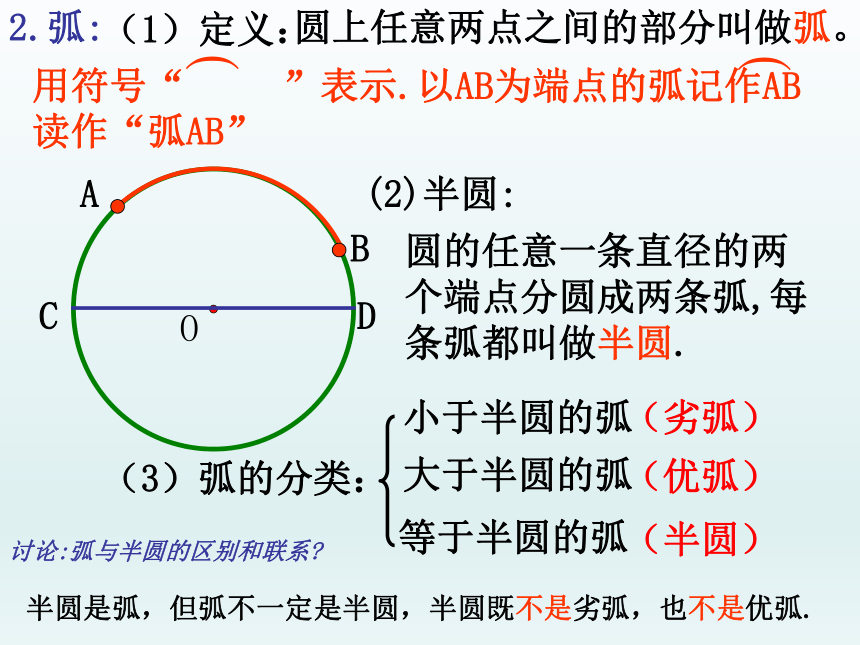
(1)定义:
圆上任意两点之间的部分叫做弧。
(3)弧的分类:
小于半圆的弧
大于半圆的弧
等于半圆的弧
(劣弧)
(优弧)
(半圆)
讨论:弧与半圆的区别和联系
2.弧:
O
A
B
C
D
(2)半圆:
圆的任意一条直径的两个端点分圆成两条弧,每条弧都叫做半圆.
用符号“ ”表示.以AB为端点的弧记作AB
读作“弧AB”
半圆是弧,但弧不一定是半圆,半圆既不是劣弧,也不是优弧.
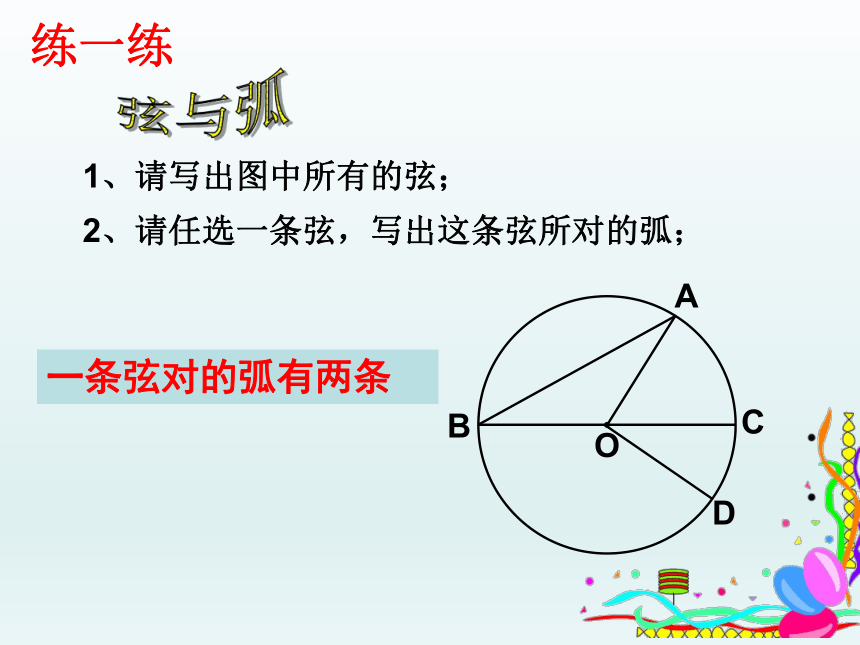
1、请写出图中所有的弦;
2、请任选一条弦,写出这条弦所对的弧;
A
B
C
O
D
一条弦对的弧有两条
练一练
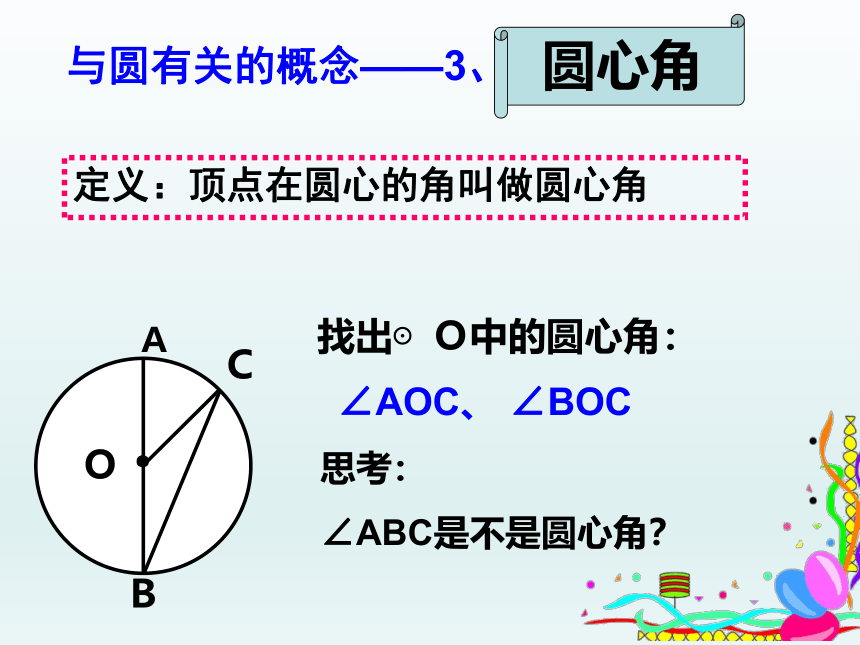
圆心角
定义:顶点在圆心的角叫做圆心角
A
O·
B
C
找出⊙O中的圆心角:
∠AOC、 ∠BOC
思考:
∠ABC是不是圆心角?
与圆有关的概念——3、
B
A
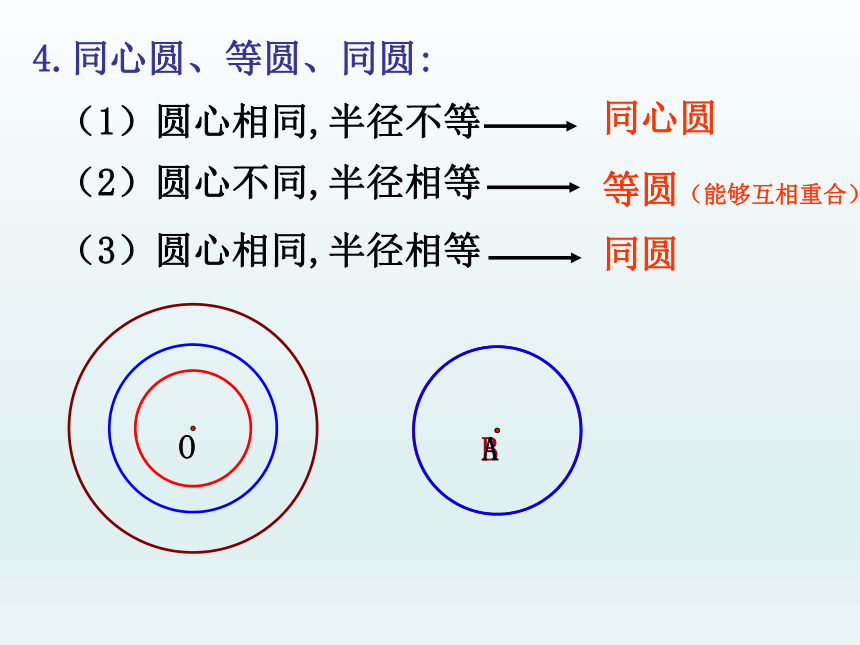
(1)圆心相同,半径不等
(2)圆心不同,半径相等
(3)圆心相同,半径相等
同心圆
等圆(能够互相重合)
同圆
O
4.同心圆、等圆、同圆:
讨论:请说出同圆、等圆、同心圆的区别和联系
同圆是指同一个圆,等圆、同心圆都是指两个圆;
同心圆圆心相同。
同圆、等圆半径相等 。
O
O
P
5.等弧:
P
O
A
B
C
D
能够互相重合的弧叫等弧
在同圆或等圆中,
讨论:“长度相等的弧叫做等弧”这种说法对吗
1、抢答:(判断正误 )
(1)弦是直径;
(2)半圆是弧,但弧不一定是半圆;
(5)圆心相同,半径相等的两个圆是同心圆;
(6)半径相等的两个圆是等圆.
(3)半圆是最长的弧;
(4)直径是最长的弦;
课堂大比武:
(7)若P是⊙O内一点,过P点的最长的弦有一条。
2、下列说法错误的是( )
A、圆上的点到圆心的距离相等
B、过圆心的线段是直径
C、直径是圆中最长的弦
D、半径相等的圆是等圆
3、下列说法:①直径是弦 ②弦是直径 ③半圆是弧,但弧不一定是半圆 ④长度相等的两条弧是等弧⑤完全重合的两条弧是等弧。
正确的命题有( )
A、1个 B、2个 C、3个 D、4个
B
C
课堂练习:
1、如图, 是直径,
有 条弦, 、 是劣弧,
是优弧。
ADC、
2
A
D
C
B
O
AC
CD
CAD
AD
2.如图,点A、B、C、D都在⊙O上,在图中画出
以这4点为端点的各条弦,这样的弦共有多少条
O
D
A
B
C
课堂练习:
三.例题
例.已知:如图,点A、B和点C、D分别在两个同
心圆上,且∠AOB=∠COD.∠C与∠D相等吗
为什么
O
B
D
A
C
解: ∠C与∠D相等。
∵∠AOB=∠COD
∴∠BOC=∠AOD
∵ OB=OA,OC=OD
∴ △BOC≌ △AOD
∴ ∠C=∠D
3.(1)在图中,画出⊙O的两条直径;
(2)依次连接这两条直径的端点,得一个
四边形判断这个四边形的型状,并说明理由.
B
C
O
D
A
课堂练习:
如图, AB是⊙O的直径,C是BA延长线上一点,
点D在⊙O上,且CD=OA,CD的延长线交⊙O于点E。
判断∠E与∠C的关系并证明.
A
D
O
B
C
E
思考与探索:
如图, AB是⊙O的直径,C是BA延长线上一点,
点D在⊙O上,且CD=OA,CD的延长线交⊙O于点E。
若∠C=20°, 求∠BOE的度数.
A
D
O
B
C
E
20
20
40
40
60°
思考与探索:
变化:如图, AB是⊙O的直径,C是BA延长线上一点,
点D在⊙O上,且CD=OA,CD的延长线交⊙O于点E。
求证:∠BOE=3∠C.
5.如图,⊙O的直径AB=4,半径OC⊥AB,D为
BC上一动点,DE⊥OC,DF⊥AB,垂足分别为E、F.
问在运动过程中EF的长是否发生变化 如果变化
请说明理由;若不变,则求出EF长.
E
F
C
A
O
B
D
课堂练习:
H
G
I
J
L
K
E
A
O
B
F
D
C
练习:
6.如图,在⊙O中,半径OE垂直于直径AB,C、D、F
为半圆上三点,过这三点分别向直径AB和半径
OE作垂线段,得矩形CKOL、DJOI、FGOI.
试判断线段KL、JI、HG之间的数量关系,并说明
理由.
想一想:
已知:一点到圆周上的最大距离为8,
最小距离为2.
则:该圆的直径等于 .
6或10
小结:
1、圆的相关概念
2、利用同圆中半径相等为构造全等三角形或等腰三角形提供条件。
经过圆心的弦(如图中的AC)叫做直径.
·
O
· C
连接圆上任意两点的线段叫做弦.
A ·
·B
与圆有关的概念—— 1、
讨论:
直径和弦的区别和联系
直径是弦,但弦不一定是直径;
直径是圆中最大的弦.
如图(1)直径是_______;
(2)弦是_____________;
(3) PQ是直径吗 ______;
(4)线段EF、GH
是弦吗?_______.
即时考你:
.
O
A
D
Q
C
B
P
H
G
F
E
K
AB
CD、DK、AB
不是
不是
在圆中有长度不等的弦,
直径是圆中最长的弦。
1、弦的两个端点在圆上
2、直径是弦,是过圆心的弦
3、半径不是弦,因为圆心不在圆周上
注 意:
圆的任意一条直径的两个端点把圆分成的两条弧,每一条弧都叫做半圆.
·
O
与圆有关的概念——2、
圆上任意两点间的部分叫做圆弧,简称弧.以A、B为端点的弧记作 ,读作“圆弧AB”或“弧AB”.
AB
A ·
· B
·C
大于半圆的弧有_____________
(用三个字母表示)
·
O
A ·
· B
·C
图中共有____条弧,
其中比半圆小的弧是__________
AB、
BC
ACB、
BAC
6
小于半圆的弧叫做劣弧
大于半圆的弧叫做优弧
与圆有关的概念——
(1)定义:
圆上任意两点之间的部分叫做弧。
(3)弧的分类:
小于半圆的弧
大于半圆的弧
等于半圆的弧
(劣弧)
(优弧)
(半圆)
讨论:弧与半圆的区别和联系
2.弧:
O
A
B
C
D
(2)半圆:
圆的任意一条直径的两个端点分圆成两条弧,每条弧都叫做半圆.
用符号“ ”表示.以AB为端点的弧记作AB
读作“弧AB”
半圆是弧,但弧不一定是半圆,半圆既不是劣弧,也不是优弧.
1、请写出图中所有的弦;
2、请任选一条弦,写出这条弦所对的弧;
A
B
C
O
D
一条弦对的弧有两条
练一练
圆心角
定义:顶点在圆心的角叫做圆心角
A
O·
B
C
找出⊙O中的圆心角:
∠AOC、 ∠BOC
思考:
∠ABC是不是圆心角?
与圆有关的概念——3、
B
A
(1)圆心相同,半径不等
(2)圆心不同,半径相等
(3)圆心相同,半径相等
同心圆
等圆(能够互相重合)
同圆
O
4.同心圆、等圆、同圆:
讨论:请说出同圆、等圆、同心圆的区别和联系
同圆是指同一个圆,等圆、同心圆都是指两个圆;
同心圆圆心相同。
同圆、等圆半径相等 。
O
O
P
5.等弧:
P
O
A
B
C
D
能够互相重合的弧叫等弧
在同圆或等圆中,
讨论:“长度相等的弧叫做等弧”这种说法对吗
1、抢答:(判断正误 )
(1)弦是直径;
(2)半圆是弧,但弧不一定是半圆;
(5)圆心相同,半径相等的两个圆是同心圆;
(6)半径相等的两个圆是等圆.
(3)半圆是最长的弧;
(4)直径是最长的弦;
课堂大比武:
(7)若P是⊙O内一点,过P点的最长的弦有一条。
2、下列说法错误的是( )
A、圆上的点到圆心的距离相等
B、过圆心的线段是直径
C、直径是圆中最长的弦
D、半径相等的圆是等圆
3、下列说法:①直径是弦 ②弦是直径 ③半圆是弧,但弧不一定是半圆 ④长度相等的两条弧是等弧⑤完全重合的两条弧是等弧。
正确的命题有( )
A、1个 B、2个 C、3个 D、4个
B
C
课堂练习:
1、如图, 是直径,
有 条弦, 、 是劣弧,
是优弧。
ADC、
2
A
D
C
B
O
AC
CD
CAD
AD
2.如图,点A、B、C、D都在⊙O上,在图中画出
以这4点为端点的各条弦,这样的弦共有多少条
O
D
A
B
C
课堂练习:
三.例题
例.已知:如图,点A、B和点C、D分别在两个同
心圆上,且∠AOB=∠COD.∠C与∠D相等吗
为什么
O
B
D
A
C
解: ∠C与∠D相等。
∵∠AOB=∠COD
∴∠BOC=∠AOD
∵ OB=OA,OC=OD
∴ △BOC≌ △AOD
∴ ∠C=∠D
3.(1)在图中,画出⊙O的两条直径;
(2)依次连接这两条直径的端点,得一个
四边形判断这个四边形的型状,并说明理由.
B
C
O
D
A
课堂练习:
如图, AB是⊙O的直径,C是BA延长线上一点,
点D在⊙O上,且CD=OA,CD的延长线交⊙O于点E。
判断∠E与∠C的关系并证明.
A
D
O
B
C
E
思考与探索:
如图, AB是⊙O的直径,C是BA延长线上一点,
点D在⊙O上,且CD=OA,CD的延长线交⊙O于点E。
若∠C=20°, 求∠BOE的度数.
A
D
O
B
C
E
20
20
40
40
60°
思考与探索:
变化:如图, AB是⊙O的直径,C是BA延长线上一点,
点D在⊙O上,且CD=OA,CD的延长线交⊙O于点E。
求证:∠BOE=3∠C.
5.如图,⊙O的直径AB=4,半径OC⊥AB,D为
BC上一动点,DE⊥OC,DF⊥AB,垂足分别为E、F.
问在运动过程中EF的长是否发生变化 如果变化
请说明理由;若不变,则求出EF长.
E
F
C
A
O
B
D
课堂练习:
H
G
I
J
L
K
E
A
O
B
F
D
C
练习:
6.如图,在⊙O中,半径OE垂直于直径AB,C、D、F
为半圆上三点,过这三点分别向直径AB和半径
OE作垂线段,得矩形CKOL、DJOI、FGOI.
试判断线段KL、JI、HG之间的数量关系,并说明
理由.
想一想:
已知:一点到圆周上的最大距离为8,
最小距离为2.
则:该圆的直径等于 .
6或10
小结:
1、圆的相关概念
2、利用同圆中半径相等为构造全等三角形或等腰三角形提供条件。
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
