高中物理鲁科版必修第一册课件:第2章+第2节 第2课时+速度与位移的关系(51张PPT)
文档属性
| 名称 | 高中物理鲁科版必修第一册课件:第2章+第2节 第2课时+速度与位移的关系(51张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-10-26 00:00:00 | ||
图片预览











文档简介
(共51张PPT)
第2章 匀变速直线运动
第2课时 速度与位移的关系
第2节 位移变化规律
自主学习·必备知识
教材原句
教材研习
要点 匀变速直线运动的位移-速度关系
我们可以把公式vt=v0+at和s=v0t+ at2联立,消去时间t,得到一个新的公式
- =2as ,这便是匀变速直线运动的位移-速度关系式。根据这个公式,在
没有时间信息 时,我们也可用位移与速度的关系分析物体运动的相关情况。
(1)这个公式能适用于匀减速直线运动吗
(2)公式应用时应注意什么
自主思考
提示 (1)当然可以,匀变速直线运动均可适用。
(2)公式中的物理量均为矢量,应用时注意正确使用正负号,与规定正方向相同时取正号,与规定方向相反时取负号,当求速度时开方结果注意分析其合理性。
何谓没有时间信息
提示 即问题中只有速度、位移、加速度这些相关物理量。
名师点睛
1.速度与位移关系式的推导
根据v=v0+at得出时间t= 代入s=v0t+ at2 s= v2- =2as。
2.速度与位移关系式v2- =2as的理解及应用
(1)公式的适用条件:公式表述的是匀变速直线运动的速度与位移的关系,适
用于匀变速直线运动。
(2)公式的意义:公式v2- =2as反映了初速度v0、末速度v、加速度a、位移s之
间的关系,当其中三个物理量已知时,可求第四个未知的量。
(3)公式的矢量性:公式中v0、v、a、s都是矢量,解题时先要规定正方向。一
般规定v0的方向为正方向,则:
①物体做加速运动时,a取正值;做减速运动时,a取负值。
②s>0,说明物体通过的位移方向与初速度方向相同;s<0,说明位移的方向与
初速度的方向相反。或者已知位移时,位移的方向与正方向相同,取正值;位
移的方向与正方向相反,取负值。
③v>0,说明末速度的方向与初速度方向相同;v<0,说明末速度的方向与初速
度方向相反。
注意 应用此公式时,注意物理量的符号,必要时对计算结果进行分析,验证
其合理性。
(4)两种特殊形式
①当v0=0时,v2=2as(初速度为零的匀加速直线运动)。
②当v=0时,- =2as(末速度为零的匀减速直线运动,例如刹车问题)。
互动探究·关键能力
探究点一 速度与位移的关系
仔细观察图片,体会如何根据刹车痕迹的长度判断汽车的行驶速度。
交通事故中,交警为了判断汽车是否超速,只要知道刹车时的加速度大小,再
测出刹车痕迹的长度,就可以求得汽车开始刹车时的速度。这是怎么办到的
情境探究
提示 根据速度与位移的关系式v2- =2as,末速度v为零,测量出刹车距离s,并
将已知的加速度a代入关系式,即可计算出汽车开始刹车时的速度v0。
探究归纳
1.公式v2- =2as是矢量式,解题时一定要先设定正方向,一般取v0方向为正方
向。
2.当运动物体不能看作质点时,要考虑物体的长度,注意位移s的取值。
探究应用
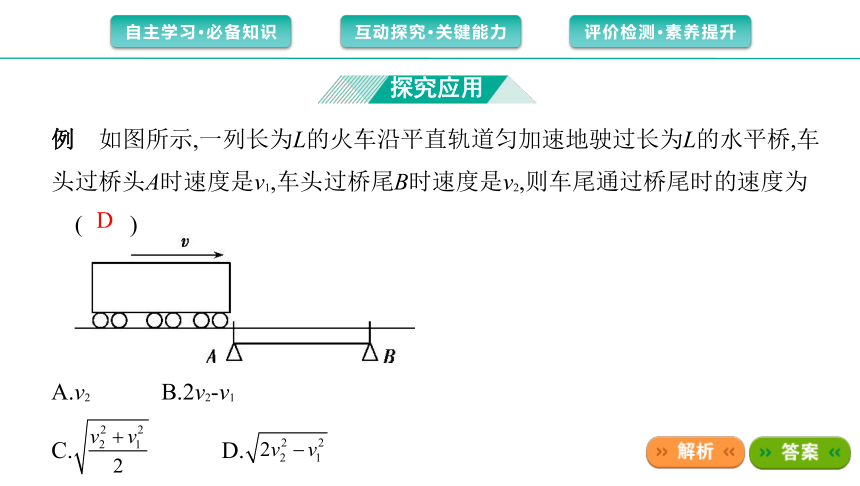
例 如图所示,一列长为L的火车沿平直轨道匀加速地驶过长为L的水平桥,车
头过桥头A时速度是v1,车头过桥尾B时速度是v2,则车尾通过桥尾时的速度为
( )
A.v2 B.2v2-v1
C. D.
D
解析 火车车头从桥头到桥尾运动的过程中有:2aL= - ,火车车头从桥
头到车尾通过桥尾的过程中有:2a·2L=v2- ,得v= 。故D项正确。
解题感悟
对位移-速度关系的理解及应用
1.当给出初速度、末速度、加速度,研究位移时,适合选用公式v2- =2ax。
2.公式v2- =2ax是矢量式,注意a的正负取值。
3.当运动物体不能看作质点时,要考虑物体的长度,注意位移x的取值。
迁移应用
1.(2021广东广州四十七中高一期中)如图甲,一辆小汽车在长度为L=21 m的
平直桥面上提速,图乙是该车在该段的车速的二次方(v2)与位移(s)的关系。
则小汽车通过该段平直桥面的加速度和时间分别为 ( )
A.4 m/s2 6 s B.2 m/s2 3 s
C.2 m/s2 5 s D.2 m/s2 s
B
解析 本题考查速度位移公式,根据图像信息结合速度位移公式可解
答。由题图乙是该车在该段的车速的二次方(v2)与位移(s)的关系可知,题图
乙中信息可知运用公式v2- =2as,解得a=2 m/s2,再由公式a= ,得t=3 s,故选
B。
2.物体做初速度为零的匀加速直线运动,加速度为2 m/s2,经过一段时间发生
的位移为16 m。则物体的末速度为 ( )
A.2 m/s B.6 m/s
C.8 m/s D.10 m/s
C
解析 由速度位移关系式可知v2- =2as,解得物体的末速度为v=
=8 m/s,故C正确。
探究点二 匀变速直线运动中间位置的速度
知识深化
1.内容:匀变速直线运动中,位移中点的瞬时速度 与初速度v0、末速度v的关
系是 = 。
2.推导:对前一半位移有 - =2as,对后一半位移有v2- =2a ,两式联立可得
= 。
3.中间时刻的瞬时速度 与位移中点的瞬时速度 的比较
在v-t图像中,速度图线与时间轴围成的面积表示位移。当物体做匀加速直线
运动时,由图甲可知 > ;当物体做匀减速直线运动时,由图乙可知 > 。所
以当物体做匀变速直线运动时, > 。
结论:无论是匀加速运动还是匀减速运动,均有 > 。
题组过关
1.物体从斜面顶端由静止开始匀加速下滑,到达斜面底端时速度为4 m/s,则物
体经过斜面中点时的速度为 ( )
A.2 m/s B.2 m/s
C. m/s D. m/s
解析 对整个过程有v2=2as,对物体下滑到斜面中点的过程有v'2=2a ,解
得v'= v=2 m/s,则B正确。
B
2.一个做匀减速直线运动的物体,先后经过a、b两点时的速度大小分别是4v
和v,所用时间为t,则下列判断正确的是 ( )
A.物体的加速度大小为
B.物体经过ab中点时的速率是 v
C.物体在 时刻的速率是2v
D.物体在这段时间内的位移为2.5vt
D
解析 物体的加速度大小为a= = ,A错误;物体经过ab中点时的速
率为v'= = v,B错误;物体在 时刻的速率为v″= = =2.5v,C错
误;物体在这段时间内的位移s= t=2.5vt,D正确。
探究点三 初速度为零的匀变速直线运动的特殊规律
知识深化
1.设物体做v0=0,加速度为a的匀加速直线运动,从t=0时刻开始计时,以T为单
位时间,则:
(1)1T末、2T末、3T末、…、nT末瞬时速度之比为v1∶v2∶v3∶…∶vn=1∶
2∶3∶…∶n。
由v=at可证。
(2)1T内、2T内、3T内、…、nT内位移之比为x1∶x2∶x3∶…∶xn=12∶22∶3
2∶…∶n2。
由s= at2可证。
(3)第1个T内、第2个T内、第3个T内、…、第n个T内位移之比为s1∶s2∶s3∶
…∶sn=1∶3∶5∶…∶(2n-1)。
证明:s1=d1= aT2、s2=d2-d1= aT2、s3=d3-d2= aT2……
2.设物体做v0=0,加速度为a的匀加速直线运动,从t=0时刻开始计时,以s为单位
位移,如图所示,则存在以下几个关系式:
(1)通过连续相等的位移时的瞬时速度之比为v1∶v2∶v3∶…∶vn=1∶ ∶
∶…∶
由v2=2as可证。
(2)通过前s、前2s、前3s、…、前ns的位移所用时间之比为T1∶T2∶T3∶
…∶Tn=1∶ ∶ ∶…∶
由s= at2得t= 可证。
(3)通过连续相等的位移所用时间之比为t1∶t2∶t3∶…∶tn=1∶( -1)∶( -
)∶…∶( - )
由T1∶T2∶T3∶…∶Tn=1∶ ∶ ∶…∶ 可证。
注意 对做匀减速运动的物体速度减为零的过程用逆向思维,同样适用!
题组过关
1.一质点从静止开始做匀加速直线运动,则在第1个2 s、第2个2 s和第5 s内的
三段位移之比为 ( )
A.2∶6∶5 B.2∶8∶7
C.4∶12∶9 D.2∶2∶1
C
解析 方法一:设质点的加速度为a,则第1个2 s内的位移s1= a×22=2a,第2
个2 s内的位移s2= a×42- a×22=6a,第5 s内的位移s3= a×52- a×42= a,则s1∶s
2∶s3=4∶12∶9,C正确。
方法二:由连续相等时间内通过的位移比为1∶3∶5∶7∶9∶…∶(2n-1)可得,
第1 s内、第2 s内、…、第5 s内的位移之比为1∶3∶5∶7∶9,则第1个2 s、
第2个2 s和第5 s内的位移之比为4∶12∶9。
2.(多选)如图所示,完全相同的三个木块并排固定在水平面上,一颗子弹以某
一速度水平射入,若子弹在木块中做匀减速直线运动,且穿过第3块木块后速
度恰好为零,则子弹依次射入每块木块时的速度比和穿过每块木块所需时间
比分别为 ( )
A.v1∶v2∶v3=3∶2∶1
B.v1∶v2∶v3= ∶ ∶1
BD
C.t1∶t2∶t3=1∶ ∶
D.t1∶t2∶t3=( - )∶( -1)∶1
解析 逆向思维:子弹向右做初速度为零的匀加速直线运动,则通过连
续相等的位移时的瞬时速度之比为v3∶v2∶v1=1∶ ∶ ,B正确;通过连续
相等的位移所用时间之比为t3∶t2∶t1=1∶( -1)∶( - ),D正确。
课堂检测
评价检测·素养提升
1.某物体做初速度为零的匀加速直线运动,当其运动速度等于其末速度的
时,剩余的路程占其全程的 ( )
A. B. C. D.
解析 令末速度为v,加速度为a,则根据位移速度关系式v2=2as,当物体速
度由 到v的过程中物体的位移为x'= ,由两式解得 = ,故选D。
D
2.一个由静止开始做匀加速直线运动的物体,如果运动的第1秒内的位移是2
m,则物体运动第4秒内的位移是 ( )
A.8 m B.14 m C.16 m D.32 m
B
解析 初速度为零的匀加速直线运动在连续相等时间内的位移之比为
1∶3∶5∶7∶…∶(2n-1),即可求解出第4秒内的位移为s4=7s1=7×2 m=14 m,故
选B。
3.(★)如图所示,左图是我国新研制的两种型号穿甲弹A1和A2,右图是被穿透
的钢板,若它们的出膛初速度分别可达1.8 km/s和1.5 km/s,能穿透同一种钢板
厚度的极限值分别为600 mm和450 mm,那它们穿透钢板过程的加速度之比
约为 ( )
A.36∶25 B.9∶10 C.27∶25 D.25∶23
解析 由速度-位移公式v2- =2as可知, = × = ,故C正确。
C
素养视角
科学思维
刹车类问题
实际交通工具刹车后可认为是做匀减速直线运动,当速度减小到零时,车辆就
会停止。解答此类问题的思路是:
(1)先求出它从刹车到停止的刹车时间t刹= ;
(2)比较所给时间与刹车时间的关系确定运动时间,最后再利用运动学公式求
解。若t>t刹,不能盲目把时间代入;若t解。
1.汽车以20 m/s的速度在平直公路上行驶,急刹车时的加速度大小为5 m/s2,则
从驾驶员急踩刹车开始,2 s内与5 s内汽车的位移大小之比为 ( )
A.5∶4 B.4∶5 C.3∶4 D.4∶3
素养演练
解析 汽车刹车到停止所需的时间t= = s=4 s,2 s时的位移x1=v0t-
at2=20×2 m- ×5×22 m=30 m,5 s时车已停止运动,其位移等于4 s时的位移x2=
= m=40 m,故2 s与5 s时汽车的位移之比为3∶4。故选C。
C
2.一辆汽车以20 m/s的速度沿平直公路行驶,突然发现前方有障碍物,立即刹
车,汽车做匀减速直线运动,加速度大小为4 m/s2。从刹车开始计时,6秒内的
位移x的大小与第6秒末的速度v的大小分别为 ( )
A.x=48 m,v=4 m/s B.x=50 m,v=0
C.x=48 m,v=0 D.x=50 m,v=4 m/s
解析 刹车时间为t0= = s=5 s,6秒内的位移x的大小x=v0t0- a =50 m,
第6秒末的速度v的大小v=0,B正确。
B
1.做匀加速直线运动的质点,速度从v增大到2v的过程中位移为s1;速度从2v增
大到3v的过程中位移为s2,则s1∶s2等于 ( )
A.1∶1 B.1∶2 C.2∶3 D.3∶5
解析 根据位移速度关系可知(2v)2-v2=2as1,(3v)2-(2v)2=2as2,则s1∶s2=3∶5,选D。
D
2.(2021陕西榆林十二中高一月考)一滑雪运动员由静止开始沿足够长的斜坡
匀加速下滑。当下滑距离为l时,速度为v,那么,当他的速度是 时,下滑的距离
是 ( )
A. B. C. D.
解析 当速度为v时,根据速度位移公式有v2=2al,当速度为 时,根据速度位移
公式有 =2al',解得l'= ,故C正确。
C
3.一颗子弹以大小为v的速度射进一墙壁但未穿出,射入深度为s,如果子弹在
墙内穿行时做匀变速直线运动,则子弹在墙内运动的加速度大小为 ( )
A. B. C. D.
C
解析 根据0-v2=2as,解得a=- ,即加速度大小为 。故选C。
4.一物体以初速度v0=20 m/s沿光滑斜面匀减速向上滑动,当上滑距离x0=30 m
时,速度减为10 m/s,物体恰滑到斜面顶部停下,则斜面长度为 ( )
A.40 m B.50 m C.32 m D.60 m
解析 设斜面长度为L,根据速度位移关系式得v2- =2as0,0- =2aL,解得L=40 m。
A
5.一辆汽车由静止开始做匀加速直线运动,从开始运动到驶过第一个100 m距
离时,速度增加了10 m/s,汽车驶过第二个100 m时,速度的增加量 ( )
A.小于10 m/s B.等于10 m/s
C.大于10 m/s D.无法确定
A
解析 初速度为零的匀加速直线运动的加速度a= = m/s2=0.5 m/s2,根
据 - =2as,得v2= = m/s=10 m/s,则速度的增加量
Δv=(10 -10) m/s≈4.1 m/s<10 m/s。
6.汽车在平直公路上做初速度为零的匀加速直线运动,途中用了10 s的时间
通过一座长120 m的桥,过桥后汽车的速度为16 m/s,汽车自身长度忽略不计,
则 ( )
A.汽车的加速度为1.6 m/s2
B.汽车过桥头时的速度为12 m/s
C.汽车从出发到过完桥所用时间为16 s
D.汽车从出发点到桥头的距离为40 m
D
解析 汽车通过桥的平均速度 = = m/s=12 m/s,又 = ,v=16 m/s,故汽
车经过桥头的速度v0=8 m/s,汽车的加速度a= = m/s2=0.8 m/s2;汽车
从出发到过完桥所用时间为t= = s=20 s;从出发点到桥头的距离s= =
m=40 m。
7.如图所示,水平地面上并排固定着三个相同木块,一可视为质点的子弹以速
度v0从左侧水平射入1号木块,且刚好未从3号木块穿出。若子弹整个过程可
视为匀减速直线运动,则子弹离开2号木块开始进入3号木块时的速度为 ( )
A. v0 B. v0 C. v0 D. v0
B
解析 整个过程可视为匀减速直线运动,且刚好未从3号木块穿出,末速度v=
0,由v2- =2as可得v2- =-2a·3s,解得a= ,子弹由木块1进入到刚好离开木块2
过程 - =-2a·2s,将a的值代入解得v2= v0。
8.(多选)(2021江西上饶玉山樟村中学)酒后驾驶会导致许多安全隐患,因为驾
驶员的反应时间变长,反应时间是指驾驶员从发现情况到采取制动的时间。
表中“思考距离”是指驾驶员从发现情况到采取制动的时间内汽车行驶的
距离,“制动距离”是指驾驶员从发现情况到汽车停止行驶的距离(假设汽车
制动时的加速度大小都相等)。
速度/(m·s-1) 思考距离/m 制动距离/m
正常 酒后 正常 酒后
15 7.5 15.0 22.5 30.0
20 10.0 20.0 36.7 46.7
25 12.5 25.0 54.2 s
分析表格可知,下列说法正确的是 ( )
A.驾驶员酒后反应时间比正常情况下多0.5 s
B.若汽车以20 m/s的速度行驶时,发现前方40 m处有险情,酒后驾驶不能安全
停车
C.汽车制动时,加速度大小为10 m/s2
D.表中s为66.7 m
ABD
解析 取速度为15 m/s进行计算,正常反应时间t1= = s=0.5 s,酒后
反应时间t2= = s=1 s,其余速度下计算反应时间同理,因此驾驶员酒后反应
时间比正常情况下多0.5 s,故A正确;若以20 m/s的速度行驶时,酒后停车距离
为46.7 m大于40 m,故不能安全停车,故B正确;汽车制动时做匀减速直线运动,
根据第一组数据计算,s=22.5 m-7.5 m=15 m,根据速度位移公式 - =2as,代入
数据解得a=-7.5 m/s2,C错误;当初速度为25 m/s时,停车距离为s= +25 m=
66.7 m,故D正确。
9.我国航母“山东号”上的舰载机仍采用滑跃起飞方式。某舰载机在航母
的水平直跑道上起飞时发动机产生的最大加速度大小为5 m/s2,无风环境下
飞机起飞时的速度大小至少为50 m/s。
(1)若航母静止在水面上,飞机靠自身的发动机从航母上起飞至少需要多长的
跑道
(2)为了使飞机在100 m的短跑道上起飞,若航母正以一定的速度做匀速直线
运动,则飞机起飞前,飞机和航母的共同速度至少应为多大 (结果用根式表示)
(3)如果风速不可忽略,为了使舰载机尽快起飞,飞机应当逆风行驶还是顺风
行驶并说明理由。
答案 (1)250 m (2)(50-10 ) m/s (3)见解析
解析 (1)根据v2=2as可得跑道长度
s= = m=250 m
(2)对飞机v2- =2as1
对航母s2=v0t
且v-v0=at,s1-s2=L
解得v0=(50-10 ) m/s(另一值不符合题意舍掉)
(3)舰载机机翼的横截面形状利用了在气体中流速越大的地方压强越小的原
理;飞机逆风起飞时,飞机的速度不需要增加到很大,飞机就可相对空气有一
个较大的相对速度,从而获得足够的升力,即逆风行驶,下方空气流速越大对
起飞越有利。
易错警示 本题的第(2)问注意飞机在加速过程中航母也在运动,飞机加速的
位移不等于跑道的长度,运用运动学公式解题时速度、加速度、位移要相对
同一参考系。
第2章 匀变速直线运动
第2课时 速度与位移的关系
第2节 位移变化规律
自主学习·必备知识
教材原句
教材研习
要点 匀变速直线运动的位移-速度关系
我们可以把公式vt=v0+at和s=v0t+ at2联立,消去时间t,得到一个新的公式
- =2as ,这便是匀变速直线运动的位移-速度关系式。根据这个公式,在
没有时间信息 时,我们也可用位移与速度的关系分析物体运动的相关情况。
(1)这个公式能适用于匀减速直线运动吗
(2)公式应用时应注意什么
自主思考
提示 (1)当然可以,匀变速直线运动均可适用。
(2)公式中的物理量均为矢量,应用时注意正确使用正负号,与规定正方向相同时取正号,与规定方向相反时取负号,当求速度时开方结果注意分析其合理性。
何谓没有时间信息
提示 即问题中只有速度、位移、加速度这些相关物理量。
名师点睛
1.速度与位移关系式的推导
根据v=v0+at得出时间t= 代入s=v0t+ at2 s= v2- =2as。
2.速度与位移关系式v2- =2as的理解及应用
(1)公式的适用条件:公式表述的是匀变速直线运动的速度与位移的关系,适
用于匀变速直线运动。
(2)公式的意义:公式v2- =2as反映了初速度v0、末速度v、加速度a、位移s之
间的关系,当其中三个物理量已知时,可求第四个未知的量。
(3)公式的矢量性:公式中v0、v、a、s都是矢量,解题时先要规定正方向。一
般规定v0的方向为正方向,则:
①物体做加速运动时,a取正值;做减速运动时,a取负值。
②s>0,说明物体通过的位移方向与初速度方向相同;s<0,说明位移的方向与
初速度的方向相反。或者已知位移时,位移的方向与正方向相同,取正值;位
移的方向与正方向相反,取负值。
③v>0,说明末速度的方向与初速度方向相同;v<0,说明末速度的方向与初速
度方向相反。
注意 应用此公式时,注意物理量的符号,必要时对计算结果进行分析,验证
其合理性。
(4)两种特殊形式
①当v0=0时,v2=2as(初速度为零的匀加速直线运动)。
②当v=0时,- =2as(末速度为零的匀减速直线运动,例如刹车问题)。
互动探究·关键能力
探究点一 速度与位移的关系
仔细观察图片,体会如何根据刹车痕迹的长度判断汽车的行驶速度。
交通事故中,交警为了判断汽车是否超速,只要知道刹车时的加速度大小,再
测出刹车痕迹的长度,就可以求得汽车开始刹车时的速度。这是怎么办到的
情境探究
提示 根据速度与位移的关系式v2- =2as,末速度v为零,测量出刹车距离s,并
将已知的加速度a代入关系式,即可计算出汽车开始刹车时的速度v0。
探究归纳
1.公式v2- =2as是矢量式,解题时一定要先设定正方向,一般取v0方向为正方
向。
2.当运动物体不能看作质点时,要考虑物体的长度,注意位移s的取值。
探究应用
例 如图所示,一列长为L的火车沿平直轨道匀加速地驶过长为L的水平桥,车
头过桥头A时速度是v1,车头过桥尾B时速度是v2,则车尾通过桥尾时的速度为
( )
A.v2 B.2v2-v1
C. D.
D
解析 火车车头从桥头到桥尾运动的过程中有:2aL= - ,火车车头从桥
头到车尾通过桥尾的过程中有:2a·2L=v2- ,得v= 。故D项正确。
解题感悟
对位移-速度关系的理解及应用
1.当给出初速度、末速度、加速度,研究位移时,适合选用公式v2- =2ax。
2.公式v2- =2ax是矢量式,注意a的正负取值。
3.当运动物体不能看作质点时,要考虑物体的长度,注意位移x的取值。
迁移应用
1.(2021广东广州四十七中高一期中)如图甲,一辆小汽车在长度为L=21 m的
平直桥面上提速,图乙是该车在该段的车速的二次方(v2)与位移(s)的关系。
则小汽车通过该段平直桥面的加速度和时间分别为 ( )
A.4 m/s2 6 s B.2 m/s2 3 s
C.2 m/s2 5 s D.2 m/s2 s
B
解析 本题考查速度位移公式,根据图像信息结合速度位移公式可解
答。由题图乙是该车在该段的车速的二次方(v2)与位移(s)的关系可知,题图
乙中信息可知运用公式v2- =2as,解得a=2 m/s2,再由公式a= ,得t=3 s,故选
B。
2.物体做初速度为零的匀加速直线运动,加速度为2 m/s2,经过一段时间发生
的位移为16 m。则物体的末速度为 ( )
A.2 m/s B.6 m/s
C.8 m/s D.10 m/s
C
解析 由速度位移关系式可知v2- =2as,解得物体的末速度为v=
=8 m/s,故C正确。
探究点二 匀变速直线运动中间位置的速度
知识深化
1.内容:匀变速直线运动中,位移中点的瞬时速度 与初速度v0、末速度v的关
系是 = 。
2.推导:对前一半位移有 - =2as,对后一半位移有v2- =2a ,两式联立可得
= 。
3.中间时刻的瞬时速度 与位移中点的瞬时速度 的比较
在v-t图像中,速度图线与时间轴围成的面积表示位移。当物体做匀加速直线
运动时,由图甲可知 > ;当物体做匀减速直线运动时,由图乙可知 > 。所
以当物体做匀变速直线运动时, > 。
结论:无论是匀加速运动还是匀减速运动,均有 > 。
题组过关
1.物体从斜面顶端由静止开始匀加速下滑,到达斜面底端时速度为4 m/s,则物
体经过斜面中点时的速度为 ( )
A.2 m/s B.2 m/s
C. m/s D. m/s
解析 对整个过程有v2=2as,对物体下滑到斜面中点的过程有v'2=2a ,解
得v'= v=2 m/s,则B正确。
B
2.一个做匀减速直线运动的物体,先后经过a、b两点时的速度大小分别是4v
和v,所用时间为t,则下列判断正确的是 ( )
A.物体的加速度大小为
B.物体经过ab中点时的速率是 v
C.物体在 时刻的速率是2v
D.物体在这段时间内的位移为2.5vt
D
解析 物体的加速度大小为a= = ,A错误;物体经过ab中点时的速
率为v'= = v,B错误;物体在 时刻的速率为v″= = =2.5v,C错
误;物体在这段时间内的位移s= t=2.5vt,D正确。
探究点三 初速度为零的匀变速直线运动的特殊规律
知识深化
1.设物体做v0=0,加速度为a的匀加速直线运动,从t=0时刻开始计时,以T为单
位时间,则:
(1)1T末、2T末、3T末、…、nT末瞬时速度之比为v1∶v2∶v3∶…∶vn=1∶
2∶3∶…∶n。
由v=at可证。
(2)1T内、2T内、3T内、…、nT内位移之比为x1∶x2∶x3∶…∶xn=12∶22∶3
2∶…∶n2。
由s= at2可证。
(3)第1个T内、第2个T内、第3个T内、…、第n个T内位移之比为s1∶s2∶s3∶
…∶sn=1∶3∶5∶…∶(2n-1)。
证明:s1=d1= aT2、s2=d2-d1= aT2、s3=d3-d2= aT2……
2.设物体做v0=0,加速度为a的匀加速直线运动,从t=0时刻开始计时,以s为单位
位移,如图所示,则存在以下几个关系式:
(1)通过连续相等的位移时的瞬时速度之比为v1∶v2∶v3∶…∶vn=1∶ ∶
∶…∶
由v2=2as可证。
(2)通过前s、前2s、前3s、…、前ns的位移所用时间之比为T1∶T2∶T3∶
…∶Tn=1∶ ∶ ∶…∶
由s= at2得t= 可证。
(3)通过连续相等的位移所用时间之比为t1∶t2∶t3∶…∶tn=1∶( -1)∶( -
)∶…∶( - )
由T1∶T2∶T3∶…∶Tn=1∶ ∶ ∶…∶ 可证。
注意 对做匀减速运动的物体速度减为零的过程用逆向思维,同样适用!
题组过关
1.一质点从静止开始做匀加速直线运动,则在第1个2 s、第2个2 s和第5 s内的
三段位移之比为 ( )
A.2∶6∶5 B.2∶8∶7
C.4∶12∶9 D.2∶2∶1
C
解析 方法一:设质点的加速度为a,则第1个2 s内的位移s1= a×22=2a,第2
个2 s内的位移s2= a×42- a×22=6a,第5 s内的位移s3= a×52- a×42= a,则s1∶s
2∶s3=4∶12∶9,C正确。
方法二:由连续相等时间内通过的位移比为1∶3∶5∶7∶9∶…∶(2n-1)可得,
第1 s内、第2 s内、…、第5 s内的位移之比为1∶3∶5∶7∶9,则第1个2 s、
第2个2 s和第5 s内的位移之比为4∶12∶9。
2.(多选)如图所示,完全相同的三个木块并排固定在水平面上,一颗子弹以某
一速度水平射入,若子弹在木块中做匀减速直线运动,且穿过第3块木块后速
度恰好为零,则子弹依次射入每块木块时的速度比和穿过每块木块所需时间
比分别为 ( )
A.v1∶v2∶v3=3∶2∶1
B.v1∶v2∶v3= ∶ ∶1
BD
C.t1∶t2∶t3=1∶ ∶
D.t1∶t2∶t3=( - )∶( -1)∶1
解析 逆向思维:子弹向右做初速度为零的匀加速直线运动,则通过连
续相等的位移时的瞬时速度之比为v3∶v2∶v1=1∶ ∶ ,B正确;通过连续
相等的位移所用时间之比为t3∶t2∶t1=1∶( -1)∶( - ),D正确。
课堂检测
评价检测·素养提升
1.某物体做初速度为零的匀加速直线运动,当其运动速度等于其末速度的
时,剩余的路程占其全程的 ( )
A. B. C. D.
解析 令末速度为v,加速度为a,则根据位移速度关系式v2=2as,当物体速
度由 到v的过程中物体的位移为x'= ,由两式解得 = ,故选D。
D
2.一个由静止开始做匀加速直线运动的物体,如果运动的第1秒内的位移是2
m,则物体运动第4秒内的位移是 ( )
A.8 m B.14 m C.16 m D.32 m
B
解析 初速度为零的匀加速直线运动在连续相等时间内的位移之比为
1∶3∶5∶7∶…∶(2n-1),即可求解出第4秒内的位移为s4=7s1=7×2 m=14 m,故
选B。
3.(★)如图所示,左图是我国新研制的两种型号穿甲弹A1和A2,右图是被穿透
的钢板,若它们的出膛初速度分别可达1.8 km/s和1.5 km/s,能穿透同一种钢板
厚度的极限值分别为600 mm和450 mm,那它们穿透钢板过程的加速度之比
约为 ( )
A.36∶25 B.9∶10 C.27∶25 D.25∶23
解析 由速度-位移公式v2- =2as可知, = × = ,故C正确。
C
素养视角
科学思维
刹车类问题
实际交通工具刹车后可认为是做匀减速直线运动,当速度减小到零时,车辆就
会停止。解答此类问题的思路是:
(1)先求出它从刹车到停止的刹车时间t刹= ;
(2)比较所给时间与刹车时间的关系确定运动时间,最后再利用运动学公式求
解。若t>t刹,不能盲目把时间代入;若t
1.汽车以20 m/s的速度在平直公路上行驶,急刹车时的加速度大小为5 m/s2,则
从驾驶员急踩刹车开始,2 s内与5 s内汽车的位移大小之比为 ( )
A.5∶4 B.4∶5 C.3∶4 D.4∶3
素养演练
解析 汽车刹车到停止所需的时间t= = s=4 s,2 s时的位移x1=v0t-
at2=20×2 m- ×5×22 m=30 m,5 s时车已停止运动,其位移等于4 s时的位移x2=
= m=40 m,故2 s与5 s时汽车的位移之比为3∶4。故选C。
C
2.一辆汽车以20 m/s的速度沿平直公路行驶,突然发现前方有障碍物,立即刹
车,汽车做匀减速直线运动,加速度大小为4 m/s2。从刹车开始计时,6秒内的
位移x的大小与第6秒末的速度v的大小分别为 ( )
A.x=48 m,v=4 m/s B.x=50 m,v=0
C.x=48 m,v=0 D.x=50 m,v=4 m/s
解析 刹车时间为t0= = s=5 s,6秒内的位移x的大小x=v0t0- a =50 m,
第6秒末的速度v的大小v=0,B正确。
B
1.做匀加速直线运动的质点,速度从v增大到2v的过程中位移为s1;速度从2v增
大到3v的过程中位移为s2,则s1∶s2等于 ( )
A.1∶1 B.1∶2 C.2∶3 D.3∶5
解析 根据位移速度关系可知(2v)2-v2=2as1,(3v)2-(2v)2=2as2,则s1∶s2=3∶5,选D。
D
2.(2021陕西榆林十二中高一月考)一滑雪运动员由静止开始沿足够长的斜坡
匀加速下滑。当下滑距离为l时,速度为v,那么,当他的速度是 时,下滑的距离
是 ( )
A. B. C. D.
解析 当速度为v时,根据速度位移公式有v2=2al,当速度为 时,根据速度位移
公式有 =2al',解得l'= ,故C正确。
C
3.一颗子弹以大小为v的速度射进一墙壁但未穿出,射入深度为s,如果子弹在
墙内穿行时做匀变速直线运动,则子弹在墙内运动的加速度大小为 ( )
A. B. C. D.
C
解析 根据0-v2=2as,解得a=- ,即加速度大小为 。故选C。
4.一物体以初速度v0=20 m/s沿光滑斜面匀减速向上滑动,当上滑距离x0=30 m
时,速度减为10 m/s,物体恰滑到斜面顶部停下,则斜面长度为 ( )
A.40 m B.50 m C.32 m D.60 m
解析 设斜面长度为L,根据速度位移关系式得v2- =2as0,0- =2aL,解得L=40 m。
A
5.一辆汽车由静止开始做匀加速直线运动,从开始运动到驶过第一个100 m距
离时,速度增加了10 m/s,汽车驶过第二个100 m时,速度的增加量 ( )
A.小于10 m/s B.等于10 m/s
C.大于10 m/s D.无法确定
A
解析 初速度为零的匀加速直线运动的加速度a= = m/s2=0.5 m/s2,根
据 - =2as,得v2= = m/s=10 m/s,则速度的增加量
Δv=(10 -10) m/s≈4.1 m/s<10 m/s。
6.汽车在平直公路上做初速度为零的匀加速直线运动,途中用了10 s的时间
通过一座长120 m的桥,过桥后汽车的速度为16 m/s,汽车自身长度忽略不计,
则 ( )
A.汽车的加速度为1.6 m/s2
B.汽车过桥头时的速度为12 m/s
C.汽车从出发到过完桥所用时间为16 s
D.汽车从出发点到桥头的距离为40 m
D
解析 汽车通过桥的平均速度 = = m/s=12 m/s,又 = ,v=16 m/s,故汽
车经过桥头的速度v0=8 m/s,汽车的加速度a= = m/s2=0.8 m/s2;汽车
从出发到过完桥所用时间为t= = s=20 s;从出发点到桥头的距离s= =
m=40 m。
7.如图所示,水平地面上并排固定着三个相同木块,一可视为质点的子弹以速
度v0从左侧水平射入1号木块,且刚好未从3号木块穿出。若子弹整个过程可
视为匀减速直线运动,则子弹离开2号木块开始进入3号木块时的速度为 ( )
A. v0 B. v0 C. v0 D. v0
B
解析 整个过程可视为匀减速直线运动,且刚好未从3号木块穿出,末速度v=
0,由v2- =2as可得v2- =-2a·3s,解得a= ,子弹由木块1进入到刚好离开木块2
过程 - =-2a·2s,将a的值代入解得v2= v0。
8.(多选)(2021江西上饶玉山樟村中学)酒后驾驶会导致许多安全隐患,因为驾
驶员的反应时间变长,反应时间是指驾驶员从发现情况到采取制动的时间。
表中“思考距离”是指驾驶员从发现情况到采取制动的时间内汽车行驶的
距离,“制动距离”是指驾驶员从发现情况到汽车停止行驶的距离(假设汽车
制动时的加速度大小都相等)。
速度/(m·s-1) 思考距离/m 制动距离/m
正常 酒后 正常 酒后
15 7.5 15.0 22.5 30.0
20 10.0 20.0 36.7 46.7
25 12.5 25.0 54.2 s
分析表格可知,下列说法正确的是 ( )
A.驾驶员酒后反应时间比正常情况下多0.5 s
B.若汽车以20 m/s的速度行驶时,发现前方40 m处有险情,酒后驾驶不能安全
停车
C.汽车制动时,加速度大小为10 m/s2
D.表中s为66.7 m
ABD
解析 取速度为15 m/s进行计算,正常反应时间t1= = s=0.5 s,酒后
反应时间t2= = s=1 s,其余速度下计算反应时间同理,因此驾驶员酒后反应
时间比正常情况下多0.5 s,故A正确;若以20 m/s的速度行驶时,酒后停车距离
为46.7 m大于40 m,故不能安全停车,故B正确;汽车制动时做匀减速直线运动,
根据第一组数据计算,s=22.5 m-7.5 m=15 m,根据速度位移公式 - =2as,代入
数据解得a=-7.5 m/s2,C错误;当初速度为25 m/s时,停车距离为s= +25 m=
66.7 m,故D正确。
9.我国航母“山东号”上的舰载机仍采用滑跃起飞方式。某舰载机在航母
的水平直跑道上起飞时发动机产生的最大加速度大小为5 m/s2,无风环境下
飞机起飞时的速度大小至少为50 m/s。
(1)若航母静止在水面上,飞机靠自身的发动机从航母上起飞至少需要多长的
跑道
(2)为了使飞机在100 m的短跑道上起飞,若航母正以一定的速度做匀速直线
运动,则飞机起飞前,飞机和航母的共同速度至少应为多大 (结果用根式表示)
(3)如果风速不可忽略,为了使舰载机尽快起飞,飞机应当逆风行驶还是顺风
行驶并说明理由。
答案 (1)250 m (2)(50-10 ) m/s (3)见解析
解析 (1)根据v2=2as可得跑道长度
s= = m=250 m
(2)对飞机v2- =2as1
对航母s2=v0t
且v-v0=at,s1-s2=L
解得v0=(50-10 ) m/s(另一值不符合题意舍掉)
(3)舰载机机翼的横截面形状利用了在气体中流速越大的地方压强越小的原
理;飞机逆风起飞时,飞机的速度不需要增加到很大,飞机就可相对空气有一
个较大的相对速度,从而获得足够的升力,即逆风行驶,下方空气流速越大对
起飞越有利。
易错警示 本题的第(2)问注意飞机在加速过程中航母也在运动,飞机加速的
位移不等于跑道的长度,运用运动学公式解题时速度、加速度、位移要相对
同一参考系。
同课章节目录
- 绪论 撩开物理学的神秘面纱
- 一、源自然之问
- 二、探万物之秘
- 三、采科学之益
- 四、启智慧之迪
- 第1章 运动的描述
- 第1节 空间和时间
- 第2节 质点和位移
- 第3节 速度
- 第4节 加速度
- 第2章 匀变速直线运动
- 第1节 速度变化规律
- 第2节 位移变化规律
- 第3节 实验中的误差和有效数字
- 第4节 科学测量:做直线运动物体的瞬时速度
- 第5节 自由落体运动
- 第3章 相互作用
- 第1节 重力与重心
- 第2节 科学探究:弹力
- 第3节 摩擦力
- 第4章 力与平衡
- 第1节 科学探究:力的合成
- 第2节 力的分解
- 第3节 共点力的平衡
- 第5章 牛顿运动定律
- 第1节 牛顿第一运动定律
- 第2节 科学探究:加速度与力、质量的关系
- 第3节 牛顿第二运动定律
- 第4节 牛顿第三运动定律
- 第5节 超重与失重
