2021-2022学年冀教新版九年级上册数学《第27章 反比例函数》单元测试卷(word版含答案)
文档属性
| 名称 | 2021-2022学年冀教新版九年级上册数学《第27章 反比例函数》单元测试卷(word版含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 433.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-26 00:00:00 | ||
图片预览




文档简介
2021-2022学年冀教新版九年级上册数学《第27章 反比例函数》单元测试卷
一.选择题
1.下列函数中,不是反比例函数的是( )
A.x= B.y=(k≠0)
C.y= D.y=﹣
2.函数y=kx﹣2与y=(k≠0)在同一坐标系内的图象可能是( )
A. B.
C. D.
3.当路程s一定时(s≠0),速度v是时间t的( )
A.正比例函数 B.反比例函数 C.一次函数 D.无法确定
4.下列函数中是反比例函数的是( )
A.y=x﹣1 B.y= C.y= D.=1
5.如图,直线L与双曲线交于A、C两点,将直线L绕点O顺时针旋转α度角(0°<α≤45°),与双曲线交于B、D两点,则四边形ABCD形状一定是( )
A.平行四边形 B.菱形 C.矩形 D.任意四边形
6.如图,双曲线y=﹣的一个分支为( )
A.① B.② C.③ D.④
7.如图,已知点A是反比例函数y=(x>0)的图象上的一个动点,连接OA,OB⊥OA,且OB=2OA,那么经过点B的反比例函数图象的表达式为( )
A.y=﹣ B.y= C.y=﹣ D.y=
8.函数y=与y=kx﹣k(k为常数且k≠0)在同一平面直角坐标系中的图象可能是( )
A. B.
C. D.
9.已知点(﹣1,y1),(﹣2,y2),(,y3)都在反比例函数y=的图象上,则y1、y2、y3的大小关系是( )
A.y1<y2<y3 B.y3<y1<y2 C.y2<y1<y3 D.y3<y2<y1
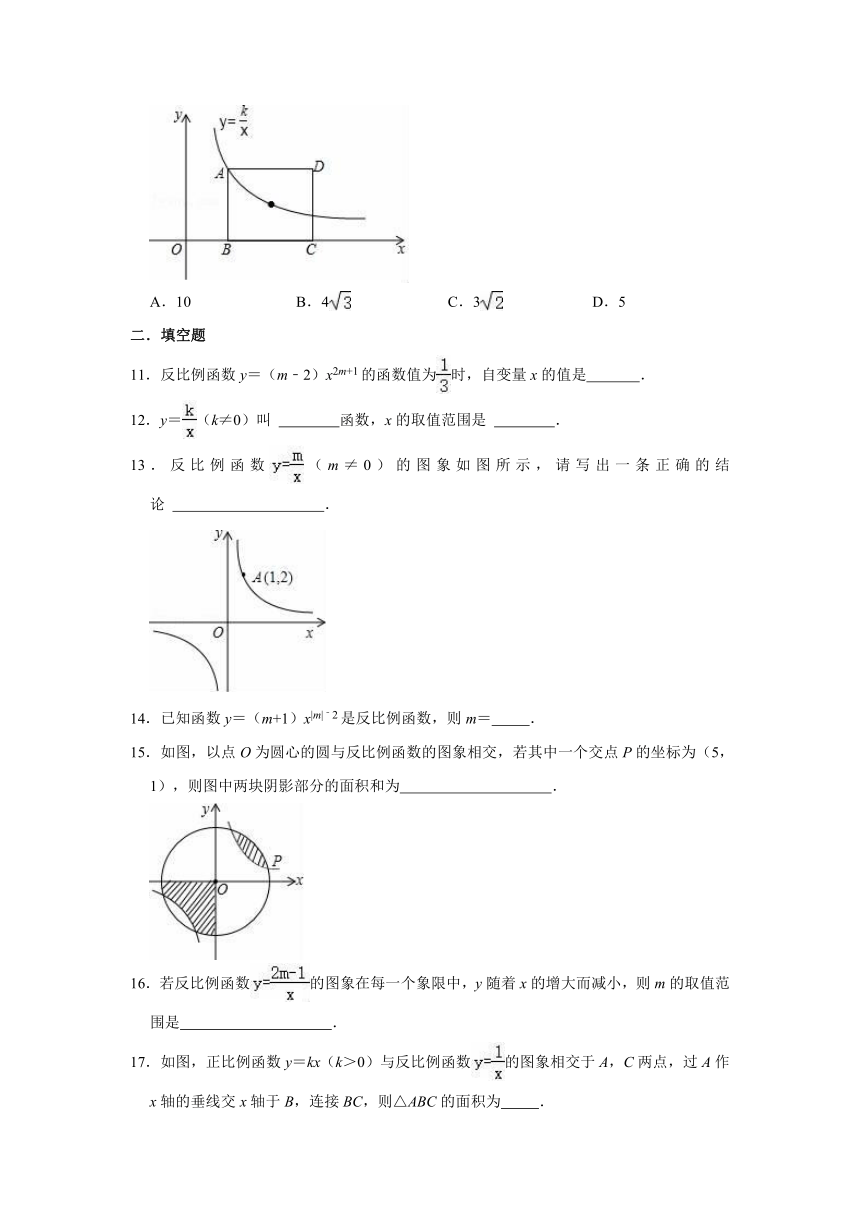
10.如图,矩形ABCD的顶点A和对称中心在反比例函数y=(k≠0,x>0)的图象上,若矩形ABCD的面积为10,则k的值为( )
A.10 B.4 C.3 D.5
二.填空题
11.反比例函数y=(m﹣2)x2m+1的函数值为时,自变量x的值是 .
12.y=(k≠0)叫 函数,x的取值范围是 .
13.反比例函数(m≠0)的图象如图所示,请写出一条正确的结论 .
14.已知函数y=(m+1)x|m|﹣2是反比例函数,则m= .
15.如图,以点O为圆心的圆与反比例函数的图象相交,若其中一个交点P的坐标为(5,1),则图中两块阴影部分的面积和为 .
16.若反比例函数的图象在每一个象限中,y随着x的增大而减小,则m的取值范围是 .
17.如图,正比例函数y=kx(k>0)与反比例函数的图象相交于A,C两点,过A作x轴的垂线交x轴于B,连接BC,则△ABC的面积为 .
18.已知点(2,﹣2)在反比例函数y=的图象上,则这个反比例函数的表达式是 .
19.如图,点A、C为反比例函数y1=﹣上的动点,点B、D为反比例函数y2=上的动点,若四边形ABCD为菱形,则该菱形边长的最小值为 .
20.如图,点A为函数y=(x>0)图象上一点,连接OA,交函数y=(x>0)的图象于点B,点C是x轴上一点,且AO=AC,则△ABC的面积为 .
三.解答题
21.已知反比例函数y=﹣
(1)说出这个函数的比例系数;
(2)求当x=﹣10时函数y的值;
(3)求当y=6时自变量x的值.
22.如果函数y=m是一个经过二、四象限的反比例函数,求m的值和反比例函数的解析式.
23.已知函数 y=(5m﹣3)x2﹣n+(n+m),
(1)当m,n为何值时是一次函数?
(2)当m,n为何值时,为正比例函数?
(3)当m,n为何值时,为反比例函数?
24.已知正比例函数y=x和反比例函数的图象(如图),请你画出函数的大致图象,并用文字说明所画图象的特征.
25.若一个函数当自变量在不同范围内取值时,函数表达式不同,我们称这样的函数为分段函数.下面我们参照学习函数的过程与方法,探究分段函数y=的图象与性质,探究过程如下,请补充完整.
(1)列表:
x … ﹣3 ﹣ ﹣2 ﹣ ﹣1 ﹣ 0 1 2 3 …
y … m 1 2 1 0 1 n …
其中,m= ,n= .
(2)描点:在平面直角坐标系中,以自变量x的取值为横坐标,以相应的函数值y为纵坐标,描出相应的点,如图所示,请画出函数的图象.
(3)研究函数并结合图象与表格,回答下列问题:
①点A(﹣6,y1),B(﹣,y2),C(x1,),D(x2,6)在函数图象上,则y1 y2,x1 x2;(填“>”,“=”或“<”)
②当函数值y=1时,求自变量x的值;
(4)若直线y=x+b与函数图象有且只有一个交点,请直接写出b的取值范围.
26.有这样一个问题:探究函数y=的图象与性质.小彤根据学习函数的经验,对函数y=的图象与性质进行了探究.
下面是小彤探究的过程,请补充完整:
(1)函数y=的自变量x的取值范围是 ;
(2)下表是y与x的几组对应值:
x … ﹣2 ﹣1 0 1 2 4 5 6 7 8 …
y … m 0 ﹣1 3 2 …
则m的值为 ;
(3)如图所示,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出了图象的一部分,请根据剩余的点补全此函数的图象;
(4)观察图象,写出该函数的一条性质 ;
(5)若函数y=的图象上有三个点A(x1,y1)、B(x2,y2)、C(x3,y3),且x1<3<x2<x3,则y1、y2、y3之间的大小关系为 ;
参考答案与试题解析
一.选择题
1.解:A、B、C选项都符合反比例函数的定义;
D选项不是反比例函数.
故选:D.
2.解:∵当k>0时,y=kx﹣2过一、三、四象限,反比例函数y=过一、三象限,
当k<0时,y=kx﹣2过二、三、四象限,反比例函数y=过二、四象限,
∴B正确;
故选:B.
3.解:v=,
当路程s一定时,速度v是时间t的反比例函数,
故选:B.
4.解:A、y=x﹣1是一次函数,不符合题意;
B、y=不是反比例函数,不符合题意;
C、y=是反比例函数,符合题意;
D、=1不是反比例函数,不符合题意;
故选:C.
5.解:由反比例函数的对称性,得
OA=OC,OB=OD,
ABCD是平行四边形,
故选:A.
6.解:∵在y=﹣中k=﹣6<0,
∴解的两个分支分别位于第二、四象限,排除③④,
又当x=﹣2时,y=3,排除②,
故正确答案应该为①.
故选:A.
7.解:过A作AC⊥y轴,BD⊥y轴,可得∠ACO=∠BDO=90°,
∵∠AOC+∠OAC=90°,∠AOC+∠BOD=90°,
∴∠OAC=∠BOD,
∴△AOC∽△OBD,
∵OB=2OA,
∴△AOC与△OBD相似比为1:2,
∴S△AOC:S△OBD=1:4,
∵点A在反比例y=上,
∴△AOC面积为,
∴△OBD面积为2,即|k|=4,
∵k<0,∴k=4,
则点B所在的反比例解析式为y=﹣,
故选:C.
8.解:A、∵由反比例函数的图象在一、三象限可知,k>0,∴﹣k<0,∴一次函数y=kx﹣k的图象经过一、三、四象限,故本选项错误;
B、∵由反比例函数的图象在二、四象限可知,k<0,∴﹣k>0,∴一次函数y=kx﹣k的图象经过一、二、四象限,故本选项错误;
C、∵由反比例函数的图象在一、三象限可知,k>0,∴﹣k<0,∴一次函数y=kx﹣k的图象经过一、三、四象限,故本选项正确;
D、∵由反比例函数的图象在一、三象限可知,k>0,∴﹣k<0,∴一次函数y=kx﹣k的图象经过一、三、四象限,故本选项错误;
故选:C.
9.解:∵反比例函数y=的k=﹣2<0,
∴函数图象的两个分式分别位于二、四象限,且在每一象限内y随x的增大而增大.
∵﹣2<0,﹣1<0,
∴点(﹣1,y1),(﹣2,y2)位于第二象限,
∴y1>0,y2>0,
∵﹣1>﹣2<0,
∴0<y2<y1.
∵2>0,
∴点(,y3)位于第四象限,
∴y3<0,
∴y3<y2<y1.
故选:D.
10.设 A(),
∴AB=,
∵矩形的面积为10,
∴BC=,
∴矩形对称中心的坐标为:(),即()
∵对称中心在的图象上,
∴,
∴mk﹣5m=0,
∴m(k﹣5)=0,
∴m=0(不符合题意,舍去)或k=5,
故选:D.
二.填空题
11.解:∵y=(m﹣2)x2m+1是反比例函数,
则有,
解得m=﹣1,
因而函数解析式是y=,
当函数值为时,即,
解得x=﹣9.
故自变量x的值是﹣9.
12.解:y=(k≠0)叫反比例函数,x的取值范围是x≠0.
13.解:m=1×2,
∴函数解析式为:y=.
14.解:由题意得:,
解得m=1,
故答案为1.
15.解:∵圆和反比例函数一个交点P的坐标为(5,1),
∴可知圆的半径r=,
∵反比例函数的图象关于坐标原点对称,是中心对称图形,
∴图中两个阴影面积的和是圆的面积,
∴S阴影==.
故答案为:.
16.解:∵在每个象限内,y随着x的增大而减小,
∴2m﹣1>0,
∴m>.
故答案为:m>.
17.解:因为过双曲线上任意一点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S是个定值,
即S=|k|,
依题意有S△ABC=2S△AOB=2××|k|=1.
故答案为:1.
18.解:∵反比例函数y=(k≠0)的图象上一点的坐标为(2,﹣2),
∴k=﹣2×2=﹣4,
∴反比例函数解析式为y=﹣,
故答案为:y=﹣.
19.解:连接AC、BD,过A点作AE⊥x轴于E,过D点作DF⊥x轴于F,如图,
∵四边形ABCD为菱形,
∴AC⊥BD,
∵A为反比例函数y1=﹣上的点,点D为反比例函数y2=上的点,
∴S△AOE=|﹣6|=3,S△ODF=×2=1,
∵∠OAE+∠AOE=90°,∠AOE+∠DOF=90°,
∴∠OAE=∠DOF,
∴Rt△AOE∽Rt△ODF,
∴S△AOE:S△ODF=OA2:OD2=3:1,
∴OA:OD=:1,
∴AD==2OD,
当OD最小时,AD最小,
∵点D为反比例函数y2=的对称轴与反比例函数图象在一象限的交点时,OD最小,
∴OD的最小值为=2,
∴AD的最小值为4,
即该菱形边长的最小值为4.
故答案为4.
20.解:设点A的坐标为(a,),点B的坐标为(b,),
∵点C是x轴上一点,且AO=AC,
∴点C的坐标是(2a,0),
设过点O(0,0),A(a,)的直线的解析式为:y=kx,
∴,
解得,k=,
又∵点B(b,)在y=上,
∴,解得,或(舍去),
∴S△ABC=S△AOC﹣S△OBC==,
故答案为:6.
三.解答题
21.解:(1)原式=,比例系数为﹣;
(2)当x=﹣10时,原式=﹣=;
(3)当y=6时,﹣=6,解得,x=﹣.
22.解:∵反比例函数y=m是图象经过二、四象限,
∴m2﹣5=﹣1,m<0,解得m=﹣2,
∴解析式为y=.
23.解:(1)当函数y=(5m﹣3)x2﹣n+(m+n)是一次函数时,
2﹣n=1,且5m﹣3≠0,
解得:n=1且m≠;
(2)当函数y=(5m﹣3)x2﹣n+(m+n)是正比例函数时,,
解得:n=1,m=﹣1.
(3)当函数y=(5m﹣3)x2﹣n+(m+n)是反比例函数时,,
解得:n=3,m=﹣3.
24.解:列表:
x ﹣3 ﹣2 ﹣1 ﹣ 1 2 3
y ﹣ ﹣ 0 ﹣ 0
描点、连线:
所画图象有两个分支,两个分支关于原点对称且都不与y轴相交.
25.解:(1)x=﹣3代入y=﹣得,y=,
∴m=,
把x=3代入y=|x﹣1|中得,y=2,
∴n=2,
故答案为,2;
(2)如图所示:
(3)①由图象可知A与B在y=﹣上,y随x的增大而增大,所以y1<y2;
C与D在y=|x﹣1|上,所以x1<x2;
故答案为<,<;
②当y=1时,x>﹣1时,有1=|x﹣1|,
∴x=0或x=2,
当y=1时,x≤﹣1时,有1=﹣,
∴x=﹣2,
故x=0或x=2或x=﹣2;
(4)由图象可知,﹣1<b<2或b>3.
26.解:(1)∵x﹣3≠0,
∴x≠3;
(2)当x=﹣1时,y===;
(3)如图所示:
(4)由图象可得,当x>3时,y随x的增大而减小(答案不唯一);
(5)由图象可得,当x1<3时,y1<1;当3<x2<x3时,1<y3<y2.
∴y1、y2、y3之间的大小关系为y1<y3<y2.
故答案为:x≠3;;当x>3时,y随x的增大而减小;y1<y3<y2.
一.选择题
1.下列函数中,不是反比例函数的是( )
A.x= B.y=(k≠0)
C.y= D.y=﹣
2.函数y=kx﹣2与y=(k≠0)在同一坐标系内的图象可能是( )
A. B.
C. D.
3.当路程s一定时(s≠0),速度v是时间t的( )
A.正比例函数 B.反比例函数 C.一次函数 D.无法确定
4.下列函数中是反比例函数的是( )
A.y=x﹣1 B.y= C.y= D.=1
5.如图,直线L与双曲线交于A、C两点,将直线L绕点O顺时针旋转α度角(0°<α≤45°),与双曲线交于B、D两点,则四边形ABCD形状一定是( )
A.平行四边形 B.菱形 C.矩形 D.任意四边形
6.如图,双曲线y=﹣的一个分支为( )
A.① B.② C.③ D.④
7.如图,已知点A是反比例函数y=(x>0)的图象上的一个动点,连接OA,OB⊥OA,且OB=2OA,那么经过点B的反比例函数图象的表达式为( )
A.y=﹣ B.y= C.y=﹣ D.y=
8.函数y=与y=kx﹣k(k为常数且k≠0)在同一平面直角坐标系中的图象可能是( )
A. B.
C. D.
9.已知点(﹣1,y1),(﹣2,y2),(,y3)都在反比例函数y=的图象上,则y1、y2、y3的大小关系是( )
A.y1<y2<y3 B.y3<y1<y2 C.y2<y1<y3 D.y3<y2<y1
10.如图,矩形ABCD的顶点A和对称中心在反比例函数y=(k≠0,x>0)的图象上,若矩形ABCD的面积为10,则k的值为( )
A.10 B.4 C.3 D.5
二.填空题
11.反比例函数y=(m﹣2)x2m+1的函数值为时,自变量x的值是 .
12.y=(k≠0)叫 函数,x的取值范围是 .
13.反比例函数(m≠0)的图象如图所示,请写出一条正确的结论 .
14.已知函数y=(m+1)x|m|﹣2是反比例函数,则m= .
15.如图,以点O为圆心的圆与反比例函数的图象相交,若其中一个交点P的坐标为(5,1),则图中两块阴影部分的面积和为 .
16.若反比例函数的图象在每一个象限中,y随着x的增大而减小,则m的取值范围是 .
17.如图,正比例函数y=kx(k>0)与反比例函数的图象相交于A,C两点,过A作x轴的垂线交x轴于B,连接BC,则△ABC的面积为 .
18.已知点(2,﹣2)在反比例函数y=的图象上,则这个反比例函数的表达式是 .
19.如图,点A、C为反比例函数y1=﹣上的动点,点B、D为反比例函数y2=上的动点,若四边形ABCD为菱形,则该菱形边长的最小值为 .
20.如图,点A为函数y=(x>0)图象上一点,连接OA,交函数y=(x>0)的图象于点B,点C是x轴上一点,且AO=AC,则△ABC的面积为 .
三.解答题
21.已知反比例函数y=﹣
(1)说出这个函数的比例系数;
(2)求当x=﹣10时函数y的值;
(3)求当y=6时自变量x的值.
22.如果函数y=m是一个经过二、四象限的反比例函数,求m的值和反比例函数的解析式.
23.已知函数 y=(5m﹣3)x2﹣n+(n+m),
(1)当m,n为何值时是一次函数?
(2)当m,n为何值时,为正比例函数?
(3)当m,n为何值时,为反比例函数?
24.已知正比例函数y=x和反比例函数的图象(如图),请你画出函数的大致图象,并用文字说明所画图象的特征.
25.若一个函数当自变量在不同范围内取值时,函数表达式不同,我们称这样的函数为分段函数.下面我们参照学习函数的过程与方法,探究分段函数y=的图象与性质,探究过程如下,请补充完整.
(1)列表:
x … ﹣3 ﹣ ﹣2 ﹣ ﹣1 ﹣ 0 1 2 3 …
y … m 1 2 1 0 1 n …
其中,m= ,n= .
(2)描点:在平面直角坐标系中,以自变量x的取值为横坐标,以相应的函数值y为纵坐标,描出相应的点,如图所示,请画出函数的图象.
(3)研究函数并结合图象与表格,回答下列问题:
①点A(﹣6,y1),B(﹣,y2),C(x1,),D(x2,6)在函数图象上,则y1 y2,x1 x2;(填“>”,“=”或“<”)
②当函数值y=1时,求自变量x的值;
(4)若直线y=x+b与函数图象有且只有一个交点,请直接写出b的取值范围.
26.有这样一个问题:探究函数y=的图象与性质.小彤根据学习函数的经验,对函数y=的图象与性质进行了探究.
下面是小彤探究的过程,请补充完整:
(1)函数y=的自变量x的取值范围是 ;
(2)下表是y与x的几组对应值:
x … ﹣2 ﹣1 0 1 2 4 5 6 7 8 …
y … m 0 ﹣1 3 2 …
则m的值为 ;
(3)如图所示,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出了图象的一部分,请根据剩余的点补全此函数的图象;
(4)观察图象,写出该函数的一条性质 ;
(5)若函数y=的图象上有三个点A(x1,y1)、B(x2,y2)、C(x3,y3),且x1<3<x2<x3,则y1、y2、y3之间的大小关系为 ;
参考答案与试题解析
一.选择题
1.解:A、B、C选项都符合反比例函数的定义;
D选项不是反比例函数.
故选:D.
2.解:∵当k>0时,y=kx﹣2过一、三、四象限,反比例函数y=过一、三象限,
当k<0时,y=kx﹣2过二、三、四象限,反比例函数y=过二、四象限,
∴B正确;
故选:B.
3.解:v=,
当路程s一定时,速度v是时间t的反比例函数,
故选:B.
4.解:A、y=x﹣1是一次函数,不符合题意;
B、y=不是反比例函数,不符合题意;
C、y=是反比例函数,符合题意;
D、=1不是反比例函数,不符合题意;
故选:C.
5.解:由反比例函数的对称性,得
OA=OC,OB=OD,
ABCD是平行四边形,
故选:A.
6.解:∵在y=﹣中k=﹣6<0,
∴解的两个分支分别位于第二、四象限,排除③④,
又当x=﹣2时,y=3,排除②,
故正确答案应该为①.
故选:A.
7.解:过A作AC⊥y轴,BD⊥y轴,可得∠ACO=∠BDO=90°,
∵∠AOC+∠OAC=90°,∠AOC+∠BOD=90°,
∴∠OAC=∠BOD,
∴△AOC∽△OBD,
∵OB=2OA,
∴△AOC与△OBD相似比为1:2,
∴S△AOC:S△OBD=1:4,
∵点A在反比例y=上,
∴△AOC面积为,
∴△OBD面积为2,即|k|=4,
∵k<0,∴k=4,
则点B所在的反比例解析式为y=﹣,
故选:C.
8.解:A、∵由反比例函数的图象在一、三象限可知,k>0,∴﹣k<0,∴一次函数y=kx﹣k的图象经过一、三、四象限,故本选项错误;
B、∵由反比例函数的图象在二、四象限可知,k<0,∴﹣k>0,∴一次函数y=kx﹣k的图象经过一、二、四象限,故本选项错误;
C、∵由反比例函数的图象在一、三象限可知,k>0,∴﹣k<0,∴一次函数y=kx﹣k的图象经过一、三、四象限,故本选项正确;
D、∵由反比例函数的图象在一、三象限可知,k>0,∴﹣k<0,∴一次函数y=kx﹣k的图象经过一、三、四象限,故本选项错误;
故选:C.
9.解:∵反比例函数y=的k=﹣2<0,
∴函数图象的两个分式分别位于二、四象限,且在每一象限内y随x的增大而增大.
∵﹣2<0,﹣1<0,
∴点(﹣1,y1),(﹣2,y2)位于第二象限,
∴y1>0,y2>0,
∵﹣1>﹣2<0,
∴0<y2<y1.
∵2>0,
∴点(,y3)位于第四象限,
∴y3<0,
∴y3<y2<y1.
故选:D.
10.设 A(),
∴AB=,
∵矩形的面积为10,
∴BC=,
∴矩形对称中心的坐标为:(),即()
∵对称中心在的图象上,
∴,
∴mk﹣5m=0,
∴m(k﹣5)=0,
∴m=0(不符合题意,舍去)或k=5,
故选:D.
二.填空题
11.解:∵y=(m﹣2)x2m+1是反比例函数,
则有,
解得m=﹣1,
因而函数解析式是y=,
当函数值为时,即,
解得x=﹣9.
故自变量x的值是﹣9.
12.解:y=(k≠0)叫反比例函数,x的取值范围是x≠0.
13.解:m=1×2,
∴函数解析式为:y=.
14.解:由题意得:,
解得m=1,
故答案为1.
15.解:∵圆和反比例函数一个交点P的坐标为(5,1),
∴可知圆的半径r=,
∵反比例函数的图象关于坐标原点对称,是中心对称图形,
∴图中两个阴影面积的和是圆的面积,
∴S阴影==.
故答案为:.
16.解:∵在每个象限内,y随着x的增大而减小,
∴2m﹣1>0,
∴m>.
故答案为:m>.
17.解:因为过双曲线上任意一点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S是个定值,
即S=|k|,
依题意有S△ABC=2S△AOB=2××|k|=1.
故答案为:1.
18.解:∵反比例函数y=(k≠0)的图象上一点的坐标为(2,﹣2),
∴k=﹣2×2=﹣4,
∴反比例函数解析式为y=﹣,
故答案为:y=﹣.
19.解:连接AC、BD,过A点作AE⊥x轴于E,过D点作DF⊥x轴于F,如图,
∵四边形ABCD为菱形,
∴AC⊥BD,
∵A为反比例函数y1=﹣上的点,点D为反比例函数y2=上的点,
∴S△AOE=|﹣6|=3,S△ODF=×2=1,
∵∠OAE+∠AOE=90°,∠AOE+∠DOF=90°,
∴∠OAE=∠DOF,
∴Rt△AOE∽Rt△ODF,
∴S△AOE:S△ODF=OA2:OD2=3:1,
∴OA:OD=:1,
∴AD==2OD,
当OD最小时,AD最小,
∵点D为反比例函数y2=的对称轴与反比例函数图象在一象限的交点时,OD最小,
∴OD的最小值为=2,
∴AD的最小值为4,
即该菱形边长的最小值为4.
故答案为4.
20.解:设点A的坐标为(a,),点B的坐标为(b,),
∵点C是x轴上一点,且AO=AC,
∴点C的坐标是(2a,0),
设过点O(0,0),A(a,)的直线的解析式为:y=kx,
∴,
解得,k=,
又∵点B(b,)在y=上,
∴,解得,或(舍去),
∴S△ABC=S△AOC﹣S△OBC==,
故答案为:6.
三.解答题
21.解:(1)原式=,比例系数为﹣;
(2)当x=﹣10时,原式=﹣=;
(3)当y=6时,﹣=6,解得,x=﹣.
22.解:∵反比例函数y=m是图象经过二、四象限,
∴m2﹣5=﹣1,m<0,解得m=﹣2,
∴解析式为y=.
23.解:(1)当函数y=(5m﹣3)x2﹣n+(m+n)是一次函数时,
2﹣n=1,且5m﹣3≠0,
解得:n=1且m≠;
(2)当函数y=(5m﹣3)x2﹣n+(m+n)是正比例函数时,,
解得:n=1,m=﹣1.
(3)当函数y=(5m﹣3)x2﹣n+(m+n)是反比例函数时,,
解得:n=3,m=﹣3.
24.解:列表:
x ﹣3 ﹣2 ﹣1 ﹣ 1 2 3
y ﹣ ﹣ 0 ﹣ 0
描点、连线:
所画图象有两个分支,两个分支关于原点对称且都不与y轴相交.
25.解:(1)x=﹣3代入y=﹣得,y=,
∴m=,
把x=3代入y=|x﹣1|中得,y=2,
∴n=2,
故答案为,2;
(2)如图所示:
(3)①由图象可知A与B在y=﹣上,y随x的增大而增大,所以y1<y2;
C与D在y=|x﹣1|上,所以x1<x2;
故答案为<,<;
②当y=1时,x>﹣1时,有1=|x﹣1|,
∴x=0或x=2,
当y=1时,x≤﹣1时,有1=﹣,
∴x=﹣2,
故x=0或x=2或x=﹣2;
(4)由图象可知,﹣1<b<2或b>3.
26.解:(1)∵x﹣3≠0,
∴x≠3;
(2)当x=﹣1时,y===;
(3)如图所示:
(4)由图象可得,当x>3时,y随x的增大而减小(答案不唯一);
(5)由图象可得,当x1<3时,y1<1;当3<x2<x3时,1<y3<y2.
∴y1、y2、y3之间的大小关系为y1<y3<y2.
故答案为:x≠3;;当x>3时,y随x的增大而减小;y1<y3<y2.
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
