2021-2022学年冀教新版九年级上册数学第28章 圆单元测试卷(word解析版)
文档属性
| 名称 | 2021-2022学年冀教新版九年级上册数学第28章 圆单元测试卷(word解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 387.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-26 14:36:21 | ||
图片预览




文档简介
2021-2022学年冀教新版九年级上册数学《第28章 圆》单元测试卷
一.选择题
1.自行车车轮要做成圆形,实际上是根据圆的特征( )
A.圆是轴对称图形
B.直径是圆中最长的弦
C.圆上各点到圆心的距离相等
D.圆是中心对称图形
2.下列语句中,正确的是( )
A.同一平面上的三点确定一个圆
B.三角形的外心是三角形三边中垂线的交点
C.三角形的内心到三角形三个顶点的距离相等
D.菱形的四个顶点在同一圆上
3.如图,在平面直角坐标系中,点A、B、C的坐标分别为(1,4)、(5,4)、(1,﹣2),则△ABC外接圆的圆心坐标是( )
A.(2,3) B.(3,2) C.(1,3) D.(3,1)
4.△ABC的外心在三角形的内部,则△ABC是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.无法判断
5.已知⊙O中,=2,则弦AB和2CD的大小关系是( )
A.AB>2CD B.AB=2CD C.AB<2CD D.不能确定
6.如图,在Rt△ABC中,∠C=90°,∠A=28°,以点C为圆心,BC为半径的圆分别交AB、AC于点D、点E,则弧BD的度数为( )
A.28° B.64° C.56° D.124°
7.如图,在半径为5的⊙O中,弦AB=6,点C是优弧上一点(不与A,B重合),则cosC的值为( )
A. B. C. D.
8.已知AB是半径为6的圆的一条弦,则AB的长不可能是( )
A.8 B.10 C.12 D.14
9.如图,一副直角三角板满足∠ACB=∠EDF=90°,AC=BC,AB=DF,∠EFD=30°,将三角板DEF的直角顶点D放置于三角板ABC的斜边AB上,再将三角板DEF绕点D旋转,并使边DE与边AC交于点M,边DF与边BC于点N.当∠EDF在△ABC内绕顶点D旋转时有以下结论:
①点C,M,D,N四点共圆;
②连接CD,若AD=DB,则△ADM∽△CDN;
③若AD=DB,则DN CM=BN DM;
④若AD=DB,则CM+CN=AD;
⑤若DB=2AD,AB=6,则2≤S△DMN≤4.
其中正确结论的个数是( )
A.2 B.3 C.4 D.5
10.计算机处理任务时,经常会以圆形进度条的形式显示任务完成的百分比.下面是同一个任务进行到不同阶段时进度条的示意图:
若圆半径为1,当任务完成的百分比为x时,线段MN的长度记为d(x).下列描述正确的是( )
A.d(25%)=1
B.当x>50%时,d(x)>1
C.当x1>x2时,d(x1)>d(x2)
D.当x1+x2=100%时,d(x1)=d(x2)
二.填空题
11.在半径为6的⊙O中,长为6的弦所对的圆心角是 °.
12.如图,在Rt△ABC中,以点C为圆心,BC为半径的圆交AB于点D,交AC于点E,∠BCD=40°,则∠A= .
13.用48米长的竹篱笆在空地上,围成一个绿化场地,现有两种设计方案,一种是围成正方形的场地;另一种是围成圆形场地.现请你选择,围成 (圆形、正方形两者选一)场地面积较大.
14.已知直线l:y=x﹣4,点A(1,0),点B(0,2),设点P为直线l上一动点,当点P的坐标为 时,过P、A、B不能作出一个圆.
15.直角三角形的两条直角边长分别为6和8,那么这个三角形的外接圆半径等于 .
16.如图,点A、B、C、D在⊙O上,,则AC BD(填“>”“<”或“=”).
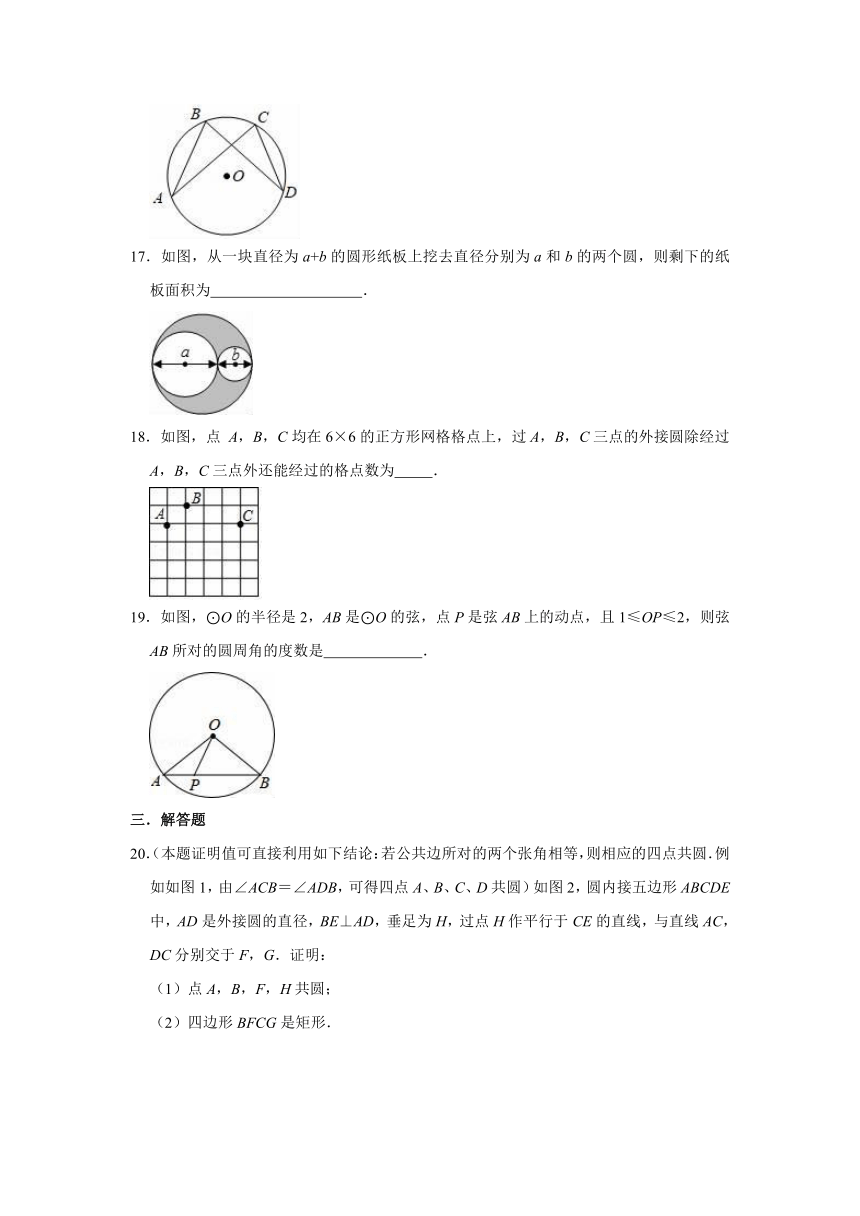
17.如图,从一块直径为a+b的圆形纸板上挖去直径分别为a和b的两个圆,则剩下的纸板面积为 .
18.如图,点 A,B,C均在6×6的正方形网格格点上,过A,B,C三点的外接圆除经过A,B,C三点外还能经过的格点数为 .
19.如图,⊙O的半径是2,AB是⊙O的弦,点P是弦AB上的动点,且1≤OP≤2,则弦AB所对的圆周角的度数是 .
三.解答题
20.(本题证明值可直接利用如下结论:若公共边所对的两个张角相等,则相应的四点共圆.例如如图1,由∠ACB=∠ADB,可得四点A、B、C、D共圆)如图2,圆内接五边形ABCDE中,AD是外接圆的直径,BE⊥AD,垂足为H,过点H作平行于CE的直线,与直线AC,DC分别交于F,G.证明:
(1)点A,B,F,H共圆;
(2)四边形BFCG是矩形.
21.如图,以△OAB的顶点O为圆心的⊙O交AB于点C、D,且AC=BD,OA与OB相等吗?为什么?
22.某地出土一个明代残破圆形瓷盘,为复制该瓷盘需确定其圆心和半径,请在图中用直尺和圆规画出瓷盘的圆心(不要求写作法、证明和讨论,但要保留作图痕迹).
23.如图,已知AB是⊙O的直径,C是⊙O上的一点,CD⊥AB于D,AD<BD,若CD=2cm,AB=5cm,求AD、AC的长.
24.如图,△ABC中,AB=AC,⊙O是△ABC的外接圆,BO的延长交边AC于点D.
(1)求证:∠BAC=2∠ABD;
(2)当△BCD是等腰三角形时,求∠BCD的大小.
25.已知,如图,在⊙O中,C、D分别是半径OA、BO的中点,求证:AD=BC.
26.如图①,在直角坐标系中,点A的坐标为(1,0),以OA为边在第一象限内作正方形OABC,点D是x轴正半轴上一动点(OD>1),连接BD,以BD为边在第一象限内作正方形DBFE,设M为正方形DBFE的中心,直线MA交y轴于点N.如果定义:只有一组对角是直角的四边形叫做损矩形.
(1)试找出图1中的一个损矩形;
(2)试说明(1)中找出的损矩形的四个顶点一定在同一个圆上;
(3)随着点D位置的变化,点N的位置是否会发生变化?若没有发生变化,求出点N的坐标;若发生变化,请说明理由;
(4)在图②中,过点M作MG⊥y轴于点G,连接DN,若四边形DMGN为损矩形,求D点坐标.
参考答案与试题解析
一.选择题
1.解:车轮做成圆形是为了在行进过程中保持和地面的高度不变,
是利用了圆上各点到圆心的距离相等,
故选:C.
2.解:A、在同一平面上但不在同一条直线上的三点确定一个圆,故选项错误;
B、三角形的外心是三角形三边中垂线的交点,故选项正确;
C、三角形的内心到三角形三边的距离相等,故选项错误;
D、菱形的四个顶点不一定在同一圆上,对角互补的四边形的四个顶点才能在同一个圆上,故选项错误.
故选:B.
3.解:根据垂径定理的推论,则
作弦AB、AC的垂直平分线,交点O1即为圆心,且坐标是(3,1).
故选:D.
4.解:若外心在三角形的外部,则三角形是钝角三角形;
若外心在三角形的内部,则三角形是锐角三角形;
若外心在三角形的边上,则三角形是直角三角形,且这边是斜边.
故选:A.
5.解:如图,取弧AB的中点E,则=,
∵=2,
∴==,
∴AE=BE=CD,
∵AE+BE>AB,
∴2CD>AB.
故选:C.
6.解:∵∠C=90°,∠A=28°,
∴∠B=62°,
∵CB=CD,
∴∠CDB=∠B=62°,
∴∠BCD=180°﹣62°﹣62°=56°,
∴的度数为56°.
故选:C.
7.解:作直径AD,连接BD,如图,
∵AD为直径,
∴∠ABD=90°,
在Rt△ABD中,∵AD=10,AB=6,
∴BD==8,
∴cosD===,
∵∠C=∠D,
∴cosC=.
故选:D.
8.解:∵圆的半径为6,
∴直径为12,
∵AB是一条弦,
∴AB的长应该小于等于12,不可能为的14,
故选:D.
9.解:①正确.理由如下:
如图1中,
∵∠ACB=90°,∠EDF=90°,
∴∠MCN+∠MDN=180°,
∴点C,M,D,N四点共圆.
②正确.理由如下:
如图2中,连接CD.
∵AC=BC.AD=DB.
∴CD⊥AB,CD=AD=DB,
∴∠ADC=∠MDN=90°,
∴∠ADM=∠CDN,
在△ADM和△CDN中,
,
∴△ADM≌△CDN.故②正确.
③正确.理由如下:
如图3中
∵CA=CB,∠ACB=90°,AD=DB,
∴CD=AD=DB,CD⊥AB,∠A=∠ACD=∠DCN=45°,
∴∠ADC=∠EDF=90°,
∴∠ADM=∠CDN,
在△ADM和△CDN中,
,
∴△ADM≌△CDN,
∴AM=CN,DM=DN,
∵AC=BC,
∴CM=BN,
∴DN CM=BN DM
④正确.理由如下:
如图4中,作DH⊥AC于H,DG⊥BC于G.
∵∠ACD=∠BCD=45°,
∴DH=DG,
∵∠DHC=∠HCG=∠CGD=90°,
∴四边形CHDG是矩形,∵DH=DG,
∴四边形CHDG是正方形,
∴∠HDG=∠MDN=90°,CH=CG,
∴∠MDH=∠GDN,
在△DHM和△DGN中,
,
∴△DHM≌△DGN,
∴MH=NG
∴CM+CN=CH+MH+CG﹣NG=2CH,
∵AD=CD=CH,
∴CM+CN=AD.
⑤正确.理由如下:
如图5中,作DH⊥AC于H,DG⊥BC于G.
∵AB=6,BD=2AD,
∴AD=2,BD=4,
∴AH=DH=,DG=GB=2,
∵∠DHC=∠HCG=∠CGD=90°,
∴四边形CHDG是矩形,
∴∠HDG=∠MDN,
∴∠MDH=∠NDG,∵∠DHM=∠DGN=90°,
∴△DHM∽△DGN,
∴==,设DM=x,则DG=2x,
∴S△DMN= 2x x=x2,
当DM⊥AC时,DM的值最小,此时DM=DH=,△DMN的面积最小值为2,
当DM⊥AB时,DM的值最大,此时DM=AD=2,△DMN的面积的最大值为4,
∴2≤S△DMN≤4.
故选:D.
10.解:A、d(25%)=>1,本选项不符合题意.
B、当x>50%时,0≤d(x)<2,本选项不符合题意.
C、当x1>x2时,d(x1)与d(x2)可能相等,可能不等,本选项不符合题意.
D、当x1+x2=100%时,d(x1)=d(x2),本选项符合题意.
故选:D.
二.填空题
11.解:∵OA=OB=AB=6,
∴△AOB为等边三角形,
∴∠AOB=60°,
故答案为:60.
12.解:∵CB=CD,
∴∠B=∠CDB,
∵∠B+∠CDB+∠BCD=180°,
∴∠B=(180°﹣∠BCD)=(180°﹣40°)=70°,
∵∠ACB=90°,
∴∠A=90°﹣∠B=20°.
故答案为20°.
13.解:围成的圆形场地的面积较大.理由如下:
设正方形的边长为a,圆的半径为R.
∵竹篱笆的长度为48米
∴4a=48,则a=12.即所围成的正方形的边长为12;2π×R=48
∴R=,即所围成的圆的半径为
∴正方形的面积S1=a2=144.圆的面积S2=π×()2=
∵144<
∴围成的圆形场地的面积较大.
故答案是:圆形.
14.解:设直线AB的解析式为y=kx+b,
∵A(1,0),点B(0,2),
∴,
解得,
∴y=﹣2x+2.
解方程组,得,
∴当P的坐标为(2,﹣2)时,过P,A,B三点不能作出一个圆.
故答案为(2,﹣2)
15.解:∵直角三角形的两条直角边长分别为6和8,
∴直角三角形的斜边==10,
所以这个三角形的外接圆的半径=×10=5,
故答案为:5.
16.解:∵=,
∴+=+,
即=,
∴AC=BD,
故答案为:=.
17.解:S阴=πab.
故答案为:πab.
18.解:如图,分别作AB、BC的中垂线,两直线的交点为O,
以O为圆心、OA为半径作圆,则⊙O即为过A,B,C三点的外接圆,
由图可知,⊙O还经过点D、E、F、G、H这5个格点,
故答案为:5.
19.解:作OD⊥AB,
∵点P是弦AB上的动点,且1≤OP≤2,
∴OD=1,
∴∠OAB=30°,
∴∠AOB=120°,
∴∠AEB=∠AOB=60°,
∵∠E+∠F=180°,
∴∠F=120°,
即弦AB所对的圆周角的度数为60°或120°,
故答案为:60°或120°.
三.解答题
20.证明:(1)由HG∥CE,得∠BHF=∠BEC,
又∵=,
∴∠BAF=∠BEC,
∴∠BAF=∠BHF,
∴点A、B、F、H共圆;
(2)由(1)的结论,得∠BHA=∠BFA,
∵BE⊥AD,
∴BF⊥AC,
又∵AD是圆的直径,
∴CG⊥AC,
由A、B、C、D共圆及A、B、F、H共圆,
∴∠BFG=∠DAB=∠BCG,
∴B、G、F、H共圆,
∴∠BGC=∠AFB=90°,
∴BG⊥GC,
∴四边形BFCG是矩形.
21.答:OA=OB.
理由如下:
如图,过O作OE⊥AB于E,
∵CD是⊙O的弦,OE⊥CD,
∴CE=DE,
∵AC=BD,
∴AE=BE,
∵OE⊥CD,
∴OA=OB.
22.解:在圆上取两个弦,根据垂径定理,
垂直平分弦的直线一定过圆心,
所以作出两弦的垂直平分线即可.
23.解:连接OC,
∵AB=5cm,
∴OC=OA=AB=cm,
Rt△CDO中,由勾股定理得:DO==cm,
∴AD=﹣=1cm,
由勾股定理得:AC==,
则AD的长为1cm,AC的长为cm.
24.解(1)连接OA并延长AO交BC于E,
∵AB=AC,
∴弧AB=弧AC,
∵AE过圆心O,
∴AE垂直平分BC(平分弧的直径垂直平分弧所对的弦),
∴AE平分∠BAC,
∴∠BAC=2∠BAE,
∵OA=OB,
∴∠ABD=∠BAE,
∴∠BAC=2∠ABD;
(2)设∠ABD=x,
由(1)知∠BAC=2∠ABD=2x,
∴∠BDC=3x,
△BCD是等腰三角形,
①若BD=BC,
则∠C=∠BDC=3x,
∵AB=AC,
∴∠ABC=∠C=3x,
在△ABC中,∠ABC+∠C+∠BAC=180°,
∴3x+3x+2x=180°,
解得x=22.5°,
∴∠BCD=3x=67.5°,
②若BC=CD,则∠BDC=∠CBD=3x,
∴∠ABC=∠ACB=4x,
在△ABC中,∠ABC+∠C+∠BAC=180°,
∴4x+4x+2x=180°,
∴x=18°,
∴∠BCD=4x=72°,
综上所述,△BCD是等腰三角形,∠BCD为67.5°或72°.
25.解:∵OA、OB是⊙O的两条半径,
∴AO=BO,
∵C、D分别是半径OA、BO的中点,
∴OC=OD,
在△OCB和△ODA中,
,
∴△OCB≌△ODA(SAS),
∴AD=BC.
26.解:(1)从图中我们可以发现四边形ADMB就是一个损矩形.
∵点M是正方形对角线的交点,
∴∠BMD=90°,
∵∠BAD=90°,
∴四边形ADMB就是一个损矩形.
(2)取BD中点H,连接MH,AH.
∵四边形OABC,BDEF是正方形,
∴△ABD,△BDM都是直角三角形,
∴HA=BD,HM=BD,
∴HA=HB=HM=HD=BD,
∴损矩形ABMD一定有外接圆.
(3)∵损矩形ABMD一定有外接圆⊙H,
∴∠MAD=∠MBD,
∵四边形BDEF是正方形,
∴∠MBD=45°,
∴∠MAD=45°,
∴∠OAN=45°,
∵OA=1,
∴ON=1,
∴N点的坐标为(0,﹣1).
(4)延长AB交MG于点P,过点M作MQ⊥x轴于点Q,
设MG=x,则四边形APMQ为正方形,
∴PM=AQ=x﹣1,
∴OG=MQ=x﹣1,
∵△MBP≌△MDQ,
∴DQ=BP=CG=x﹣2,
∴MN2=2x2,
ND2=(2x﹣2)2+12,
MD2=(x﹣1)2+(x﹣2)2,
∵四边形DMGN为损矩形,
∴2x2=(2x﹣2)2+12+(x﹣1)2+(x﹣2)2,
∴2x2﹣7x+5=0,
∴x=2.5或x=1(舍去),
∴OD=3,
∴D点坐标为(3,0).
一.选择题
1.自行车车轮要做成圆形,实际上是根据圆的特征( )
A.圆是轴对称图形
B.直径是圆中最长的弦
C.圆上各点到圆心的距离相等
D.圆是中心对称图形
2.下列语句中,正确的是( )
A.同一平面上的三点确定一个圆
B.三角形的外心是三角形三边中垂线的交点
C.三角形的内心到三角形三个顶点的距离相等
D.菱形的四个顶点在同一圆上
3.如图,在平面直角坐标系中,点A、B、C的坐标分别为(1,4)、(5,4)、(1,﹣2),则△ABC外接圆的圆心坐标是( )
A.(2,3) B.(3,2) C.(1,3) D.(3,1)
4.△ABC的外心在三角形的内部,则△ABC是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.无法判断
5.已知⊙O中,=2,则弦AB和2CD的大小关系是( )
A.AB>2CD B.AB=2CD C.AB<2CD D.不能确定
6.如图,在Rt△ABC中,∠C=90°,∠A=28°,以点C为圆心,BC为半径的圆分别交AB、AC于点D、点E,则弧BD的度数为( )
A.28° B.64° C.56° D.124°
7.如图,在半径为5的⊙O中,弦AB=6,点C是优弧上一点(不与A,B重合),则cosC的值为( )
A. B. C. D.
8.已知AB是半径为6的圆的一条弦,则AB的长不可能是( )
A.8 B.10 C.12 D.14
9.如图,一副直角三角板满足∠ACB=∠EDF=90°,AC=BC,AB=DF,∠EFD=30°,将三角板DEF的直角顶点D放置于三角板ABC的斜边AB上,再将三角板DEF绕点D旋转,并使边DE与边AC交于点M,边DF与边BC于点N.当∠EDF在△ABC内绕顶点D旋转时有以下结论:
①点C,M,D,N四点共圆;
②连接CD,若AD=DB,则△ADM∽△CDN;
③若AD=DB,则DN CM=BN DM;
④若AD=DB,则CM+CN=AD;
⑤若DB=2AD,AB=6,则2≤S△DMN≤4.
其中正确结论的个数是( )
A.2 B.3 C.4 D.5
10.计算机处理任务时,经常会以圆形进度条的形式显示任务完成的百分比.下面是同一个任务进行到不同阶段时进度条的示意图:
若圆半径为1,当任务完成的百分比为x时,线段MN的长度记为d(x).下列描述正确的是( )
A.d(25%)=1
B.当x>50%时,d(x)>1
C.当x1>x2时,d(x1)>d(x2)
D.当x1+x2=100%时,d(x1)=d(x2)
二.填空题
11.在半径为6的⊙O中,长为6的弦所对的圆心角是 °.
12.如图,在Rt△ABC中,以点C为圆心,BC为半径的圆交AB于点D,交AC于点E,∠BCD=40°,则∠A= .
13.用48米长的竹篱笆在空地上,围成一个绿化场地,现有两种设计方案,一种是围成正方形的场地;另一种是围成圆形场地.现请你选择,围成 (圆形、正方形两者选一)场地面积较大.
14.已知直线l:y=x﹣4,点A(1,0),点B(0,2),设点P为直线l上一动点,当点P的坐标为 时,过P、A、B不能作出一个圆.
15.直角三角形的两条直角边长分别为6和8,那么这个三角形的外接圆半径等于 .
16.如图,点A、B、C、D在⊙O上,,则AC BD(填“>”“<”或“=”).
17.如图,从一块直径为a+b的圆形纸板上挖去直径分别为a和b的两个圆,则剩下的纸板面积为 .
18.如图,点 A,B,C均在6×6的正方形网格格点上,过A,B,C三点的外接圆除经过A,B,C三点外还能经过的格点数为 .
19.如图,⊙O的半径是2,AB是⊙O的弦,点P是弦AB上的动点,且1≤OP≤2,则弦AB所对的圆周角的度数是 .
三.解答题
20.(本题证明值可直接利用如下结论:若公共边所对的两个张角相等,则相应的四点共圆.例如如图1,由∠ACB=∠ADB,可得四点A、B、C、D共圆)如图2,圆内接五边形ABCDE中,AD是外接圆的直径,BE⊥AD,垂足为H,过点H作平行于CE的直线,与直线AC,DC分别交于F,G.证明:
(1)点A,B,F,H共圆;
(2)四边形BFCG是矩形.
21.如图,以△OAB的顶点O为圆心的⊙O交AB于点C、D,且AC=BD,OA与OB相等吗?为什么?
22.某地出土一个明代残破圆形瓷盘,为复制该瓷盘需确定其圆心和半径,请在图中用直尺和圆规画出瓷盘的圆心(不要求写作法、证明和讨论,但要保留作图痕迹).
23.如图,已知AB是⊙O的直径,C是⊙O上的一点,CD⊥AB于D,AD<BD,若CD=2cm,AB=5cm,求AD、AC的长.
24.如图,△ABC中,AB=AC,⊙O是△ABC的外接圆,BO的延长交边AC于点D.
(1)求证:∠BAC=2∠ABD;
(2)当△BCD是等腰三角形时,求∠BCD的大小.
25.已知,如图,在⊙O中,C、D分别是半径OA、BO的中点,求证:AD=BC.
26.如图①,在直角坐标系中,点A的坐标为(1,0),以OA为边在第一象限内作正方形OABC,点D是x轴正半轴上一动点(OD>1),连接BD,以BD为边在第一象限内作正方形DBFE,设M为正方形DBFE的中心,直线MA交y轴于点N.如果定义:只有一组对角是直角的四边形叫做损矩形.
(1)试找出图1中的一个损矩形;
(2)试说明(1)中找出的损矩形的四个顶点一定在同一个圆上;
(3)随着点D位置的变化,点N的位置是否会发生变化?若没有发生变化,求出点N的坐标;若发生变化,请说明理由;
(4)在图②中,过点M作MG⊥y轴于点G,连接DN,若四边形DMGN为损矩形,求D点坐标.
参考答案与试题解析
一.选择题
1.解:车轮做成圆形是为了在行进过程中保持和地面的高度不变,
是利用了圆上各点到圆心的距离相等,
故选:C.
2.解:A、在同一平面上但不在同一条直线上的三点确定一个圆,故选项错误;
B、三角形的外心是三角形三边中垂线的交点,故选项正确;
C、三角形的内心到三角形三边的距离相等,故选项错误;
D、菱形的四个顶点不一定在同一圆上,对角互补的四边形的四个顶点才能在同一个圆上,故选项错误.
故选:B.
3.解:根据垂径定理的推论,则
作弦AB、AC的垂直平分线,交点O1即为圆心,且坐标是(3,1).
故选:D.
4.解:若外心在三角形的外部,则三角形是钝角三角形;
若外心在三角形的内部,则三角形是锐角三角形;
若外心在三角形的边上,则三角形是直角三角形,且这边是斜边.
故选:A.
5.解:如图,取弧AB的中点E,则=,
∵=2,
∴==,
∴AE=BE=CD,
∵AE+BE>AB,
∴2CD>AB.
故选:C.
6.解:∵∠C=90°,∠A=28°,
∴∠B=62°,
∵CB=CD,
∴∠CDB=∠B=62°,
∴∠BCD=180°﹣62°﹣62°=56°,
∴的度数为56°.
故选:C.
7.解:作直径AD,连接BD,如图,
∵AD为直径,
∴∠ABD=90°,
在Rt△ABD中,∵AD=10,AB=6,
∴BD==8,
∴cosD===,
∵∠C=∠D,
∴cosC=.
故选:D.
8.解:∵圆的半径为6,
∴直径为12,
∵AB是一条弦,
∴AB的长应该小于等于12,不可能为的14,
故选:D.
9.解:①正确.理由如下:
如图1中,
∵∠ACB=90°,∠EDF=90°,
∴∠MCN+∠MDN=180°,
∴点C,M,D,N四点共圆.
②正确.理由如下:
如图2中,连接CD.
∵AC=BC.AD=DB.
∴CD⊥AB,CD=AD=DB,
∴∠ADC=∠MDN=90°,
∴∠ADM=∠CDN,
在△ADM和△CDN中,
,
∴△ADM≌△CDN.故②正确.
③正确.理由如下:
如图3中
∵CA=CB,∠ACB=90°,AD=DB,
∴CD=AD=DB,CD⊥AB,∠A=∠ACD=∠DCN=45°,
∴∠ADC=∠EDF=90°,
∴∠ADM=∠CDN,
在△ADM和△CDN中,
,
∴△ADM≌△CDN,
∴AM=CN,DM=DN,
∵AC=BC,
∴CM=BN,
∴DN CM=BN DM
④正确.理由如下:
如图4中,作DH⊥AC于H,DG⊥BC于G.
∵∠ACD=∠BCD=45°,
∴DH=DG,
∵∠DHC=∠HCG=∠CGD=90°,
∴四边形CHDG是矩形,∵DH=DG,
∴四边形CHDG是正方形,
∴∠HDG=∠MDN=90°,CH=CG,
∴∠MDH=∠GDN,
在△DHM和△DGN中,
,
∴△DHM≌△DGN,
∴MH=NG
∴CM+CN=CH+MH+CG﹣NG=2CH,
∵AD=CD=CH,
∴CM+CN=AD.
⑤正确.理由如下:
如图5中,作DH⊥AC于H,DG⊥BC于G.
∵AB=6,BD=2AD,
∴AD=2,BD=4,
∴AH=DH=,DG=GB=2,
∵∠DHC=∠HCG=∠CGD=90°,
∴四边形CHDG是矩形,
∴∠HDG=∠MDN,
∴∠MDH=∠NDG,∵∠DHM=∠DGN=90°,
∴△DHM∽△DGN,
∴==,设DM=x,则DG=2x,
∴S△DMN= 2x x=x2,
当DM⊥AC时,DM的值最小,此时DM=DH=,△DMN的面积最小值为2,
当DM⊥AB时,DM的值最大,此时DM=AD=2,△DMN的面积的最大值为4,
∴2≤S△DMN≤4.
故选:D.
10.解:A、d(25%)=>1,本选项不符合题意.
B、当x>50%时,0≤d(x)<2,本选项不符合题意.
C、当x1>x2时,d(x1)与d(x2)可能相等,可能不等,本选项不符合题意.
D、当x1+x2=100%时,d(x1)=d(x2),本选项符合题意.
故选:D.
二.填空题
11.解:∵OA=OB=AB=6,
∴△AOB为等边三角形,
∴∠AOB=60°,
故答案为:60.
12.解:∵CB=CD,
∴∠B=∠CDB,
∵∠B+∠CDB+∠BCD=180°,
∴∠B=(180°﹣∠BCD)=(180°﹣40°)=70°,
∵∠ACB=90°,
∴∠A=90°﹣∠B=20°.
故答案为20°.
13.解:围成的圆形场地的面积较大.理由如下:
设正方形的边长为a,圆的半径为R.
∵竹篱笆的长度为48米
∴4a=48,则a=12.即所围成的正方形的边长为12;2π×R=48
∴R=,即所围成的圆的半径为
∴正方形的面积S1=a2=144.圆的面积S2=π×()2=
∵144<
∴围成的圆形场地的面积较大.
故答案是:圆形.
14.解:设直线AB的解析式为y=kx+b,
∵A(1,0),点B(0,2),
∴,
解得,
∴y=﹣2x+2.
解方程组,得,
∴当P的坐标为(2,﹣2)时,过P,A,B三点不能作出一个圆.
故答案为(2,﹣2)
15.解:∵直角三角形的两条直角边长分别为6和8,
∴直角三角形的斜边==10,
所以这个三角形的外接圆的半径=×10=5,
故答案为:5.
16.解:∵=,
∴+=+,
即=,
∴AC=BD,
故答案为:=.
17.解:S阴=πab.
故答案为:πab.
18.解:如图,分别作AB、BC的中垂线,两直线的交点为O,
以O为圆心、OA为半径作圆,则⊙O即为过A,B,C三点的外接圆,
由图可知,⊙O还经过点D、E、F、G、H这5个格点,
故答案为:5.
19.解:作OD⊥AB,
∵点P是弦AB上的动点,且1≤OP≤2,
∴OD=1,
∴∠OAB=30°,
∴∠AOB=120°,
∴∠AEB=∠AOB=60°,
∵∠E+∠F=180°,
∴∠F=120°,
即弦AB所对的圆周角的度数为60°或120°,
故答案为:60°或120°.
三.解答题
20.证明:(1)由HG∥CE,得∠BHF=∠BEC,
又∵=,
∴∠BAF=∠BEC,
∴∠BAF=∠BHF,
∴点A、B、F、H共圆;
(2)由(1)的结论,得∠BHA=∠BFA,
∵BE⊥AD,
∴BF⊥AC,
又∵AD是圆的直径,
∴CG⊥AC,
由A、B、C、D共圆及A、B、F、H共圆,
∴∠BFG=∠DAB=∠BCG,
∴B、G、F、H共圆,
∴∠BGC=∠AFB=90°,
∴BG⊥GC,
∴四边形BFCG是矩形.
21.答:OA=OB.
理由如下:
如图,过O作OE⊥AB于E,
∵CD是⊙O的弦,OE⊥CD,
∴CE=DE,
∵AC=BD,
∴AE=BE,
∵OE⊥CD,
∴OA=OB.
22.解:在圆上取两个弦,根据垂径定理,
垂直平分弦的直线一定过圆心,
所以作出两弦的垂直平分线即可.
23.解:连接OC,
∵AB=5cm,
∴OC=OA=AB=cm,
Rt△CDO中,由勾股定理得:DO==cm,
∴AD=﹣=1cm,
由勾股定理得:AC==,
则AD的长为1cm,AC的长为cm.
24.解(1)连接OA并延长AO交BC于E,
∵AB=AC,
∴弧AB=弧AC,
∵AE过圆心O,
∴AE垂直平分BC(平分弧的直径垂直平分弧所对的弦),
∴AE平分∠BAC,
∴∠BAC=2∠BAE,
∵OA=OB,
∴∠ABD=∠BAE,
∴∠BAC=2∠ABD;
(2)设∠ABD=x,
由(1)知∠BAC=2∠ABD=2x,
∴∠BDC=3x,
△BCD是等腰三角形,
①若BD=BC,
则∠C=∠BDC=3x,
∵AB=AC,
∴∠ABC=∠C=3x,
在△ABC中,∠ABC+∠C+∠BAC=180°,
∴3x+3x+2x=180°,
解得x=22.5°,
∴∠BCD=3x=67.5°,
②若BC=CD,则∠BDC=∠CBD=3x,
∴∠ABC=∠ACB=4x,
在△ABC中,∠ABC+∠C+∠BAC=180°,
∴4x+4x+2x=180°,
∴x=18°,
∴∠BCD=4x=72°,
综上所述,△BCD是等腰三角形,∠BCD为67.5°或72°.
25.解:∵OA、OB是⊙O的两条半径,
∴AO=BO,
∵C、D分别是半径OA、BO的中点,
∴OC=OD,
在△OCB和△ODA中,
,
∴△OCB≌△ODA(SAS),
∴AD=BC.
26.解:(1)从图中我们可以发现四边形ADMB就是一个损矩形.
∵点M是正方形对角线的交点,
∴∠BMD=90°,
∵∠BAD=90°,
∴四边形ADMB就是一个损矩形.
(2)取BD中点H,连接MH,AH.
∵四边形OABC,BDEF是正方形,
∴△ABD,△BDM都是直角三角形,
∴HA=BD,HM=BD,
∴HA=HB=HM=HD=BD,
∴损矩形ABMD一定有外接圆.
(3)∵损矩形ABMD一定有外接圆⊙H,
∴∠MAD=∠MBD,
∵四边形BDEF是正方形,
∴∠MBD=45°,
∴∠MAD=45°,
∴∠OAN=45°,
∵OA=1,
∴ON=1,
∴N点的坐标为(0,﹣1).
(4)延长AB交MG于点P,过点M作MQ⊥x轴于点Q,
设MG=x,则四边形APMQ为正方形,
∴PM=AQ=x﹣1,
∴OG=MQ=x﹣1,
∵△MBP≌△MDQ,
∴DQ=BP=CG=x﹣2,
∴MN2=2x2,
ND2=(2x﹣2)2+12,
MD2=(x﹣1)2+(x﹣2)2,
∵四边形DMGN为损矩形,
∴2x2=(2x﹣2)2+12+(x﹣1)2+(x﹣2)2,
∴2x2﹣7x+5=0,
∴x=2.5或x=1(舍去),
∴OD=3,
∴D点坐标为(3,0).
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
