沪科新版2021-2022学年八年级上册数学《第13章 三角形中的边角关系、命题与证明》单元测试卷(word版含解析)
文档属性
| 名称 | 沪科新版2021-2022学年八年级上册数学《第13章 三角形中的边角关系、命题与证明》单元测试卷(word版含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 221.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-26 16:01:00 | ||
图片预览




文档简介
2021-2022学年沪科新版八年级上册数学《第13章 三角形中的边角关系、命题与证明》单元测试卷
一.选择题
1.如图,图中三角形的个数有( )
A.6个 B.8个 C.10个 D.12个
2.( )叫做三角形
A.连接任意三点组成的图形
B.由不在同一条直线上的三条线段首尾顺次相接所成的图形
C.由三条线段组成的图形
D.以上说法均不对
3.在△ABC中,已知点D、E、F分别是边BC、AD、CE上的中点,且S△ABC=4cm2,则S△BEF的值为( )
A.2cm2 B.1cm2 C.0.5cm2 D.0.25cm2
4.下列四个图形中,线段BE是△ABC的高的图形是( )
A. B.
C. D.
5.如图,已知C,A,G三点共线,C,B,H三点共线,2∠CAD=∠BAD,2∠CBD=∠ABD,∠GAE=2∠BAE,∠EBH=2∠EBA,则∠D和∠E的关系满足( )
A.2∠E+∠D=320° B.2∠E+∠D=340°
C.2∠E+∠D=300° D.2∠E+∠D=360°
6.如图,为估计罗湖公园小池塘岸边A、B两点之间的距离,思雅学校小组在小池塘的一侧选取一点O,测得OA=28m,OB=20m,则A,B间的距离可能是( )
A.8m B.25m C.50m D.60m
7.下列命题中不正确的是( )
A.过直线外一点有且只有一条直线与已知直线平行
B.如果两条直线都与第三条直线平行,那么这两条直线也互相平行
C.如果两条直线都与第三条直线垂直,那么这两条直线也互相垂直
D.在同一平面内,如果一条直线垂直于两条平行线中的一条,那么它也垂直于另一条
8.下列命题中是真命题的是( )
A.相等的角是对顶角
B.数轴上的点与实数一一对应
C.同旁内角互补
D.无理数就是开方开不尽的数
9.如图,图中三角形的个数共有( )
A.3个 B.4个 C.5个 D.6个
10.如图,AD平分∠BAC,AE⊥BC,∠B=45°,∠C=73°,则∠DAE的度数是( )
A.62 B.31 C.17 D.14
二.填空题
11.如图中的三角形的个数是 个.
12.如图,一艘轮船按箭头所示方向行驶,C处有一灯塔,当轮船从A点行驶到B点时,∠ACB= °.
13.如图,在三角形ABC中,AC=5,BC=6,BC边上的高AD=4,若点P在边AC上(不与点A,C重合)移动,则线段BP最短时的长为 .
14.等腰三角形的一边等于3,一边等于6,则它的周长等于 .
15.命题“对顶角相等”的逆命题是 ,逆命题是 命题.(填“真”或“假”)
16.“相等的角是对顶角”的逆命题是 命题(填“真”或“假”).
17.如图,共有 个三角形.
18.如图,共有 个三角形.
19.已知BD是△ABC的中线,AB=7,BC=3,且△ABD的周长为15,则△BCD的周长为 .
20.如图,∠MON=90°,点A,B分别在射线OM,ON上运动,BE平分∠NBA,BE的反向延长线与∠BAO的平分线交于点C,则∠ACB的度数是 °.
三.解答题
21.如图,已知==,△ABC的周长是14cm,求BC的长.
22.已知,△ABC的三边长为4,9,x.
(1)求△ABC的周长的取值范围;
(2)当△ABC的周长为偶数时,求x.
23.如图所示,图中共有多少个三角形?请写出这些三角形并指出所有以E为顶点的角.
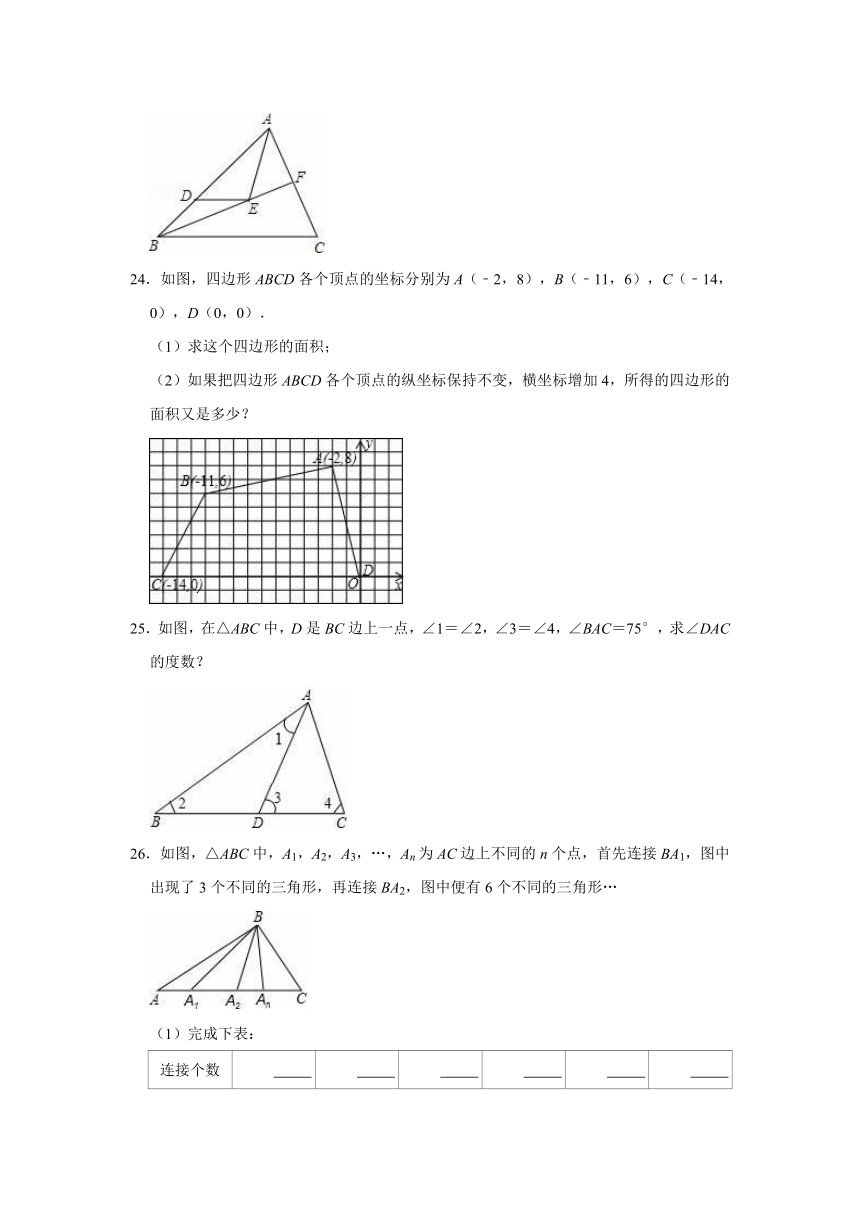
24.如图,四边形ABCD各个顶点的坐标分别为A(﹣2,8),B(﹣11,6),C(﹣14,0),D(0,0).
(1)求这个四边形的面积;
(2)如果把四边形ABCD各个顶点的纵坐标保持不变,横坐标增加4,所得的四边形的面积又是多少?
25.如图,在△ABC中,D是BC边上一点,∠1=∠2,∠3=∠4,∠BAC=75°,求∠DAC的度数?
26.如图,△ABC中,A1,A2,A3,…,An为AC边上不同的n个点,首先连接BA1,图中出现了3个不同的三角形,再连接BA2,图中便有6个不同的三角形…
(1)完成下表:
连接个数
出现三角形个数
(2)若出现了45个三角形,则共连接了多少个点?
(3)若一直连接到An,则图中共有 个三角形.
27.如图,在△ABC中,AD⊥BC,AE平分∠BAC,∠B=70°,∠C=30°.求:
(1)∠BAE的度数;
(2)∠DAE的度数;
(3)探究:小明认为如果条件∠B=70°,∠C=30°改成∠B﹣∠C=40°,也能得出∠DAE的度数?若能,请你写出求解过程;若不能,请说明理由.
参考答案与试题解析
一.选择题
1.解:图中是三角形的有:△AOD、ACD、△COD、△AOB、△BOC、△ABC、△ABD、△BCD.
故选:B.
2.解:因为三角形的定义是:由不在同一条直线上的三条线段首尾顺次相接所成的图形.
故选:B.
3.解:∵点E是AD的中点,
∴S△ABE=S△ABD,S△ACE=S△ADC,
∴S△ABE+S△ACE=S△ABC=×4=2,
∴S△BCE=S△ABC=×4=2,
∵点F是CE的中点,
∴S△BEF=S△BCE=×2=1(cm2).
故选:B.
4.解:线段BE是△ABC的高的图是选项A.
故选:A.
5.解:设∠CAD=x,∠CBD=y,则∠BAD=2x,∠ABD=2y,
∴∠GAB=180°﹣3x,∠HBA=180°﹣3y,
∵∠GAE=2∠BAE,∠EBH=2∠EBA,
∴∠BAE=60°﹣x,∠EBA=60°﹣y,
∴∠D=180°﹣2(x+y),∠E=180°﹣(60°﹣x)﹣(60°﹣y)=60°+(x+y),
∴2∠E+∠D=300°,
故选:C.
6.解:连接AB,根据三角形的三边关系定理得:
28﹣20<AB<28+20,
即:8<AB<48,
则AB的值在8和48之间.
故选:B.
7.解:A、过直线外一点有且只有一条直线与已知直线平行,是真命题;
B、如果两条直线都与第三条直线平行,那么这两条直线也互相平行,是真命题;
C、如果两条直线都与第三条直线垂直,那么这两条直线平行,原命题是假命题;
D、在同一平面内,如果一条直线垂直于两条平行线中的一条,那么它也垂直于另一条,是真命题;
故选:C.
8.解:A、相等的角不一定是对顶角,故此命题是假命题;
B、数轴上的点与实数一一对应,故此命题是真命题;
C、两直线平行,同旁内角互补,故此命题是假命题;
D、无理数有三个来源:(1)开方开不尽的数;(2)与π有关的一些运算;(3)有规律的无限不循环小数,故此命题是假命题;
故选:B.
9.解:图中是三角形的有:△AOC、△BOD、△AOB、△ABC、△ABD.
故选:C.
10.解:∵∠BAC=180°﹣∠B﹣∠C,∠B=45°,∠C=73°,
∴∠BAC=62°,
∵AD平分∠BAC,
∴∠DAC=∠BAC=31°,
∵AE⊥BC,
∴∠AEC=90°,
∴∠CAE=90°﹣73°=17°,
∴∠DAE=31°﹣17°=14°,
故选:D.
二.填空题
11.解:5+4=9(个)
故答案为:9.
12.解:∵∠CBD=∠A+∠C,
∴∠C=∠CBD﹣∠A
=70°﹣30°
=40°,
故答案为:40.
13.解:根据垂线段最短可知,当BP⊥AC时,BP最短,
∵S△ABC=×BC×AD=×AC×BP,
∴6×4=5BP,
∴PB=,
即BP最短时的值为:.
故答案为:.
14.解:当3为腰,6为底时,3+3=6,不能构成等腰三角形;
当6为腰,3为底时,3+6>6,能构成等腰三角形,周长为3+6+6=15.
故答案为:15.
15.解:命题“对顶角相等”的逆命题是:“如果两个角相等,那么这两个角是对顶角”,此逆命题为假命题.
故答案为:如果两个角相等,那么这两个角是对顶角,假.
16.解:“相等的角是对顶角”的逆命题是对顶角相等,是真命题,
故答案为:真.
17.解:图中有:△ABC,△ABD,△ABE,△ACD,△ACE,△ADE,共6个.
故答案为:6
18.解:上半部分:单个的三角形有3个,复合的三角形有2+1=3个,
所以上半部分三角形的个数为3+3=6个,
同理考虑横截线的三角形的个数也是6个.
故共有12个三角形.
19.解:∵BD是△ABC的中线,
∴AD=CD,
∵△ABD的周长为15,AB=7,BC=3,
∴△BCD的周长是15﹣(7﹣3)=11,
故答案为:11
20.解:根据三角形的外角性质,可得∠ABN=∠AOB+∠BAO,
∵BE平分∠NBA,AC平分∠BAO,
∴∠ABE=∠ABN,∠BAC=∠BAO,
∴∠C=∠ABE﹣∠BAC=(∠AOB+∠BAO)﹣∠BAO=∠AOB,
∵∠MON=90°,
∴∠AOB=90°,
∴∠C=×90°=45°.
故答案为:45.
三.解答题
21.解:∵==,
设AB为5x,BD为2x,AC为5y,CD为2y,
∵△ABC的周长是14cm,
∴5x+2x+5y+2y=14,
解得:x+y=2,
所以BC=2(x+y)=4.
22.解:(1)∵三角形的三边长分别为4,9,x,
∴9﹣4<x<9+4,即5<x<13,
∴9+4+5<△ABC的周长<9+4+13,
即:18<△ABC的周长<26;
(2)∵△ABC的周长是偶数,由(1)结果得△ABC的周长可以是20,22或24,
∴x的值为7,9或11.
23.解:图中共有7个,△AEF,△ADE,△DEB,△ABF,△BCF,△ABC,△ABE,以E为顶点的角是∠AEF,∠AED,∠DEB,∠DEF,∠AEB,∠BEF.
24.解:(1)如图,过点A作AF⊥x轴,过点B作BE⊥x轴,
则DF=2,CE=3,AF=8,BE=6,EF=﹣2﹣(﹣11)=9,
四边形ABCD的面积=S△ADF+S△BCE+S梯形ABEF,
=×2×8+×3×6+×(6+8)×9,
=8+9+63,
=80;
(2)四边形ABCD各个顶点的纵坐标保持不变,横坐标增加4,
就是把四边形ABCD向右平移4个单位,
所以,所得的四边形的面积不变,还是80.
25.解:设∠1=∠2=x,则∠3=∠4=2x.
∵∠BAC=75°,
∴∠2+∠4=180°﹣75°=105°,即x+2x=105°,
∴x=35°,
∴∠DAC=∠BAC﹣∠1=75°﹣35°=40°.
26.解:(1)
连接个数 1 2 3 4 5 6
出现三角形个数 3 6 10 15 21 28
(2)8个点;
(3)1+2+3+…+(n+1)
= [1+2+3+…+(n+1)+1+2+3+…+(n+1)]
=(n+1)(n+2).
故答案为(n+1)(n+2).
27.解:(1)∵∠B+∠C+∠BAC=180°,
∴∠BAC=180°﹣∠B﹣∠C=180°﹣70°﹣30°=80°,
∵AE平分∠BAC,
∴∠BAE=∠BAC=40°;
(2)∵AD⊥BC,
∴∠ADE=90°,
而∠ADE=∠B+∠BAD,
∴∠BAD=90°﹣∠B=90°﹣70°=20°,
∴∠DAE=∠BAE﹣∠BAD=40°﹣20°=20°;
(3)能.
∵∠B+∠C+∠BAC=180°,
∴∠BAC=180°﹣∠B﹣∠C,
∵AE平分∠BAC,
∴∠BAE=∠BAC=(180°﹣∠B﹣∠C)=90°﹣(∠B+∠C),
∵AD⊥BC,
∴∠ADE=90°,
而∠ADE=∠B+∠BAD,
∴∠BAD=90°﹣∠B,
∴∠DAE=∠BAE﹣∠BAD=90°﹣(∠B+∠C)﹣(90°﹣∠B)=(∠B﹣∠C),
∵∠B﹣∠C=40°,
∴∠DAE=×40°=20°.
一.选择题
1.如图,图中三角形的个数有( )
A.6个 B.8个 C.10个 D.12个
2.( )叫做三角形
A.连接任意三点组成的图形
B.由不在同一条直线上的三条线段首尾顺次相接所成的图形
C.由三条线段组成的图形
D.以上说法均不对
3.在△ABC中,已知点D、E、F分别是边BC、AD、CE上的中点,且S△ABC=4cm2,则S△BEF的值为( )
A.2cm2 B.1cm2 C.0.5cm2 D.0.25cm2
4.下列四个图形中,线段BE是△ABC的高的图形是( )
A. B.
C. D.
5.如图,已知C,A,G三点共线,C,B,H三点共线,2∠CAD=∠BAD,2∠CBD=∠ABD,∠GAE=2∠BAE,∠EBH=2∠EBA,则∠D和∠E的关系满足( )
A.2∠E+∠D=320° B.2∠E+∠D=340°
C.2∠E+∠D=300° D.2∠E+∠D=360°
6.如图,为估计罗湖公园小池塘岸边A、B两点之间的距离,思雅学校小组在小池塘的一侧选取一点O,测得OA=28m,OB=20m,则A,B间的距离可能是( )
A.8m B.25m C.50m D.60m
7.下列命题中不正确的是( )
A.过直线外一点有且只有一条直线与已知直线平行
B.如果两条直线都与第三条直线平行,那么这两条直线也互相平行
C.如果两条直线都与第三条直线垂直,那么这两条直线也互相垂直
D.在同一平面内,如果一条直线垂直于两条平行线中的一条,那么它也垂直于另一条
8.下列命题中是真命题的是( )
A.相等的角是对顶角
B.数轴上的点与实数一一对应
C.同旁内角互补
D.无理数就是开方开不尽的数
9.如图,图中三角形的个数共有( )
A.3个 B.4个 C.5个 D.6个
10.如图,AD平分∠BAC,AE⊥BC,∠B=45°,∠C=73°,则∠DAE的度数是( )
A.62 B.31 C.17 D.14
二.填空题
11.如图中的三角形的个数是 个.
12.如图,一艘轮船按箭头所示方向行驶,C处有一灯塔,当轮船从A点行驶到B点时,∠ACB= °.
13.如图,在三角形ABC中,AC=5,BC=6,BC边上的高AD=4,若点P在边AC上(不与点A,C重合)移动,则线段BP最短时的长为 .
14.等腰三角形的一边等于3,一边等于6,则它的周长等于 .
15.命题“对顶角相等”的逆命题是 ,逆命题是 命题.(填“真”或“假”)
16.“相等的角是对顶角”的逆命题是 命题(填“真”或“假”).
17.如图,共有 个三角形.
18.如图,共有 个三角形.
19.已知BD是△ABC的中线,AB=7,BC=3,且△ABD的周长为15,则△BCD的周长为 .
20.如图,∠MON=90°,点A,B分别在射线OM,ON上运动,BE平分∠NBA,BE的反向延长线与∠BAO的平分线交于点C,则∠ACB的度数是 °.
三.解答题
21.如图,已知==,△ABC的周长是14cm,求BC的长.
22.已知,△ABC的三边长为4,9,x.
(1)求△ABC的周长的取值范围;
(2)当△ABC的周长为偶数时,求x.
23.如图所示,图中共有多少个三角形?请写出这些三角形并指出所有以E为顶点的角.
24.如图,四边形ABCD各个顶点的坐标分别为A(﹣2,8),B(﹣11,6),C(﹣14,0),D(0,0).
(1)求这个四边形的面积;
(2)如果把四边形ABCD各个顶点的纵坐标保持不变,横坐标增加4,所得的四边形的面积又是多少?
25.如图,在△ABC中,D是BC边上一点,∠1=∠2,∠3=∠4,∠BAC=75°,求∠DAC的度数?
26.如图,△ABC中,A1,A2,A3,…,An为AC边上不同的n个点,首先连接BA1,图中出现了3个不同的三角形,再连接BA2,图中便有6个不同的三角形…
(1)完成下表:
连接个数
出现三角形个数
(2)若出现了45个三角形,则共连接了多少个点?
(3)若一直连接到An,则图中共有 个三角形.
27.如图,在△ABC中,AD⊥BC,AE平分∠BAC,∠B=70°,∠C=30°.求:
(1)∠BAE的度数;
(2)∠DAE的度数;
(3)探究:小明认为如果条件∠B=70°,∠C=30°改成∠B﹣∠C=40°,也能得出∠DAE的度数?若能,请你写出求解过程;若不能,请说明理由.
参考答案与试题解析
一.选择题
1.解:图中是三角形的有:△AOD、ACD、△COD、△AOB、△BOC、△ABC、△ABD、△BCD.
故选:B.
2.解:因为三角形的定义是:由不在同一条直线上的三条线段首尾顺次相接所成的图形.
故选:B.
3.解:∵点E是AD的中点,
∴S△ABE=S△ABD,S△ACE=S△ADC,
∴S△ABE+S△ACE=S△ABC=×4=2,
∴S△BCE=S△ABC=×4=2,
∵点F是CE的中点,
∴S△BEF=S△BCE=×2=1(cm2).
故选:B.
4.解:线段BE是△ABC的高的图是选项A.
故选:A.
5.解:设∠CAD=x,∠CBD=y,则∠BAD=2x,∠ABD=2y,
∴∠GAB=180°﹣3x,∠HBA=180°﹣3y,
∵∠GAE=2∠BAE,∠EBH=2∠EBA,
∴∠BAE=60°﹣x,∠EBA=60°﹣y,
∴∠D=180°﹣2(x+y),∠E=180°﹣(60°﹣x)﹣(60°﹣y)=60°+(x+y),
∴2∠E+∠D=300°,
故选:C.
6.解:连接AB,根据三角形的三边关系定理得:
28﹣20<AB<28+20,
即:8<AB<48,
则AB的值在8和48之间.
故选:B.
7.解:A、过直线外一点有且只有一条直线与已知直线平行,是真命题;
B、如果两条直线都与第三条直线平行,那么这两条直线也互相平行,是真命题;
C、如果两条直线都与第三条直线垂直,那么这两条直线平行,原命题是假命题;
D、在同一平面内,如果一条直线垂直于两条平行线中的一条,那么它也垂直于另一条,是真命题;
故选:C.
8.解:A、相等的角不一定是对顶角,故此命题是假命题;
B、数轴上的点与实数一一对应,故此命题是真命题;
C、两直线平行,同旁内角互补,故此命题是假命题;
D、无理数有三个来源:(1)开方开不尽的数;(2)与π有关的一些运算;(3)有规律的无限不循环小数,故此命题是假命题;
故选:B.
9.解:图中是三角形的有:△AOC、△BOD、△AOB、△ABC、△ABD.
故选:C.
10.解:∵∠BAC=180°﹣∠B﹣∠C,∠B=45°,∠C=73°,
∴∠BAC=62°,
∵AD平分∠BAC,
∴∠DAC=∠BAC=31°,
∵AE⊥BC,
∴∠AEC=90°,
∴∠CAE=90°﹣73°=17°,
∴∠DAE=31°﹣17°=14°,
故选:D.
二.填空题
11.解:5+4=9(个)
故答案为:9.
12.解:∵∠CBD=∠A+∠C,
∴∠C=∠CBD﹣∠A
=70°﹣30°
=40°,
故答案为:40.
13.解:根据垂线段最短可知,当BP⊥AC时,BP最短,
∵S△ABC=×BC×AD=×AC×BP,
∴6×4=5BP,
∴PB=,
即BP最短时的值为:.
故答案为:.
14.解:当3为腰,6为底时,3+3=6,不能构成等腰三角形;
当6为腰,3为底时,3+6>6,能构成等腰三角形,周长为3+6+6=15.
故答案为:15.
15.解:命题“对顶角相等”的逆命题是:“如果两个角相等,那么这两个角是对顶角”,此逆命题为假命题.
故答案为:如果两个角相等,那么这两个角是对顶角,假.
16.解:“相等的角是对顶角”的逆命题是对顶角相等,是真命题,
故答案为:真.
17.解:图中有:△ABC,△ABD,△ABE,△ACD,△ACE,△ADE,共6个.
故答案为:6
18.解:上半部分:单个的三角形有3个,复合的三角形有2+1=3个,
所以上半部分三角形的个数为3+3=6个,
同理考虑横截线的三角形的个数也是6个.
故共有12个三角形.
19.解:∵BD是△ABC的中线,
∴AD=CD,
∵△ABD的周长为15,AB=7,BC=3,
∴△BCD的周长是15﹣(7﹣3)=11,
故答案为:11
20.解:根据三角形的外角性质,可得∠ABN=∠AOB+∠BAO,
∵BE平分∠NBA,AC平分∠BAO,
∴∠ABE=∠ABN,∠BAC=∠BAO,
∴∠C=∠ABE﹣∠BAC=(∠AOB+∠BAO)﹣∠BAO=∠AOB,
∵∠MON=90°,
∴∠AOB=90°,
∴∠C=×90°=45°.
故答案为:45.
三.解答题
21.解:∵==,
设AB为5x,BD为2x,AC为5y,CD为2y,
∵△ABC的周长是14cm,
∴5x+2x+5y+2y=14,
解得:x+y=2,
所以BC=2(x+y)=4.
22.解:(1)∵三角形的三边长分别为4,9,x,
∴9﹣4<x<9+4,即5<x<13,
∴9+4+5<△ABC的周长<9+4+13,
即:18<△ABC的周长<26;
(2)∵△ABC的周长是偶数,由(1)结果得△ABC的周长可以是20,22或24,
∴x的值为7,9或11.
23.解:图中共有7个,△AEF,△ADE,△DEB,△ABF,△BCF,△ABC,△ABE,以E为顶点的角是∠AEF,∠AED,∠DEB,∠DEF,∠AEB,∠BEF.
24.解:(1)如图,过点A作AF⊥x轴,过点B作BE⊥x轴,
则DF=2,CE=3,AF=8,BE=6,EF=﹣2﹣(﹣11)=9,
四边形ABCD的面积=S△ADF+S△BCE+S梯形ABEF,
=×2×8+×3×6+×(6+8)×9,
=8+9+63,
=80;
(2)四边形ABCD各个顶点的纵坐标保持不变,横坐标增加4,
就是把四边形ABCD向右平移4个单位,
所以,所得的四边形的面积不变,还是80.
25.解:设∠1=∠2=x,则∠3=∠4=2x.
∵∠BAC=75°,
∴∠2+∠4=180°﹣75°=105°,即x+2x=105°,
∴x=35°,
∴∠DAC=∠BAC﹣∠1=75°﹣35°=40°.
26.解:(1)
连接个数 1 2 3 4 5 6
出现三角形个数 3 6 10 15 21 28
(2)8个点;
(3)1+2+3+…+(n+1)
= [1+2+3+…+(n+1)+1+2+3+…+(n+1)]
=(n+1)(n+2).
故答案为(n+1)(n+2).
27.解:(1)∵∠B+∠C+∠BAC=180°,
∴∠BAC=180°﹣∠B﹣∠C=180°﹣70°﹣30°=80°,
∵AE平分∠BAC,
∴∠BAE=∠BAC=40°;
(2)∵AD⊥BC,
∴∠ADE=90°,
而∠ADE=∠B+∠BAD,
∴∠BAD=90°﹣∠B=90°﹣70°=20°,
∴∠DAE=∠BAE﹣∠BAD=40°﹣20°=20°;
(3)能.
∵∠B+∠C+∠BAC=180°,
∴∠BAC=180°﹣∠B﹣∠C,
∵AE平分∠BAC,
∴∠BAE=∠BAC=(180°﹣∠B﹣∠C)=90°﹣(∠B+∠C),
∵AD⊥BC,
∴∠ADE=90°,
而∠ADE=∠B+∠BAD,
∴∠BAD=90°﹣∠B,
∴∠DAE=∠BAE﹣∠BAD=90°﹣(∠B+∠C)﹣(90°﹣∠B)=(∠B﹣∠C),
∵∠B﹣∠C=40°,
∴∠DAE=×40°=20°.
