沪科新版 2021-2022学年九年级上册数学《第23章 解直角三角形》单元测试卷(word版含解析)
文档属性
| 名称 | 沪科新版 2021-2022学年九年级上册数学《第23章 解直角三角形》单元测试卷(word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 448.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-26 16:07:28 | ||
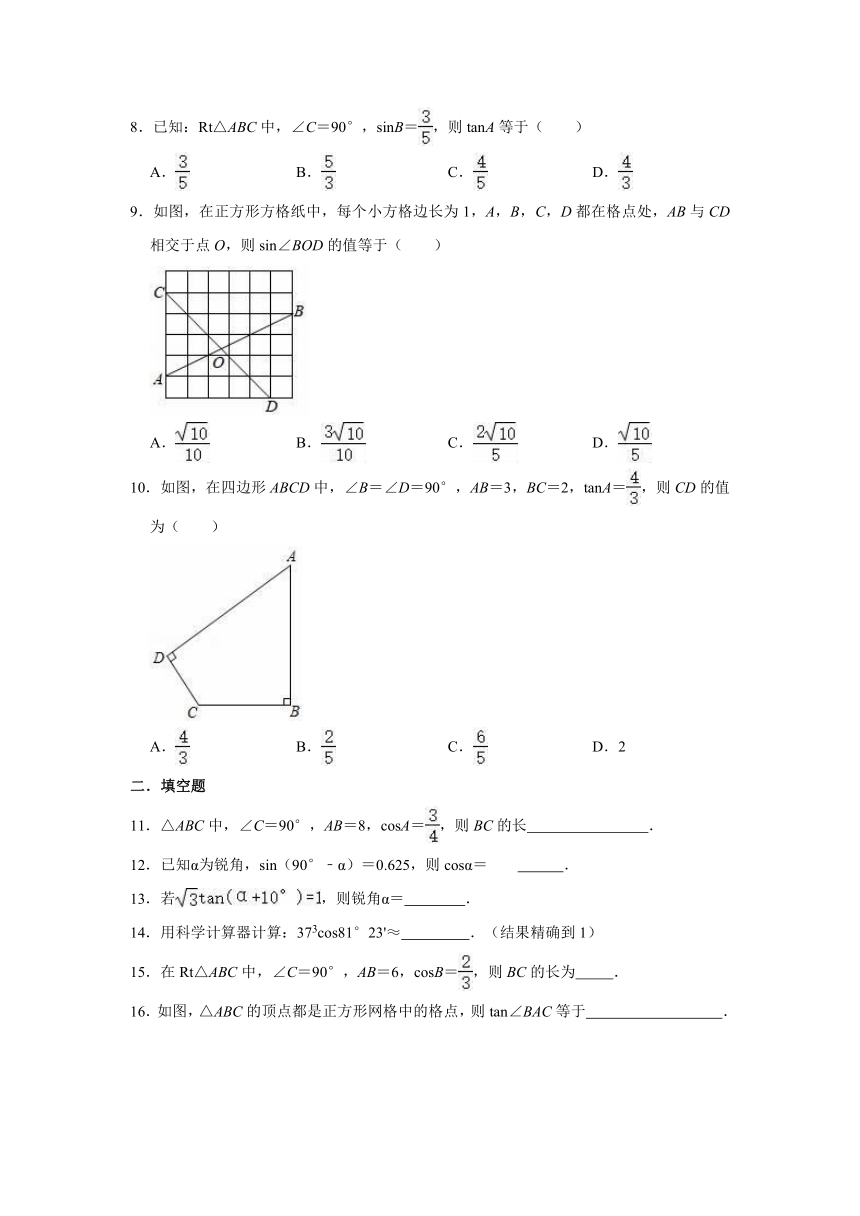
图片预览



文档简介
2021-2022学年沪科新版九年级上册数学《第23章 解直角三角形》单元测试卷
一.选择题
1.在△ABC中,∠C=90°,AC=3,BC=4,则tanA的值为( )
A. B. C. D.
2.在Rt△ABC中,∠C=90°,BC=3,AB=5,则cosB的值等于( )
A. B. C. D.
3.若0°<α<90°,则下列说法不正确的是( )
A.sinα随α的增大而增大 B.cosα随α的减小而减小
C.tanα随α的增大而增大 D.0<sinα<1
4.在△ABC中,∠C=90°,sinA=,则tanA=( )
A. B. C. D.
5.如图,在△ABC中,∠ACB=90°,∠ABC=26°,BC=5.若用科学计算器求边AC的长,则下列按键顺序正确的是( )
A.5÷tan26°= B.5÷sin26°= C.5×cos26°= D.5×tan26°=
6.等于( )
A. B.2 C.3 D.
7.如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,则cosA的值为( )
A. B. C. D.
8.已知:Rt△ABC中,∠C=90°,sinB=,则tanA等于( )
A. B. C. D.
9.如图,在正方形方格纸中,每个小方格边长为1,A,B,C,D都在格点处,AB与CD相交于点O,则sin∠BOD的值等于( )
A. B. C. D.
10.如图,在四边形ABCD中,∠B=∠D=90°,AB=3,BC=2,tanA=,则CD的值为( )
A. B. C. D.2
二.填空题
11.△ABC中,∠C=90°,AB=8,cosA=,则BC的长 .
12.已知α为锐角,sin(90°﹣α)=0.625,则cosα= .
13.若,则锐角α= .
14.用科学计算器计算:373cos81°23'≈ .(结果精确到1)
15.在Rt△ABC中,∠C=90°,AB=6,cosB=,则BC的长为 .
16.如图,△ABC的顶点都是正方形网格中的格点,则tan∠BAC等于 .
17.若∠A是锐角,cosA>,则∠A应满足 .
18.如图,在4×4的正方形方格图形中,小正方形的顶点称为格点,△ABC的顶点都在格点上,则图中cos∠ABC= .
19.已知:实常数a、b、c、d同时满足下列两个等式:①asinθ+bcosθ﹣c=0;②acosθ﹣bsinθ+d=0(其中θ为任意锐角),则a、b、c、d之间的关系式是: .
20.在Rt△ABC中,∠ACB=90°,点D是AC边上一点,连BD,过C点作BD的垂线与过A点作AC的垂线交于点E.当tan∠ABD=,cos∠E=,则的值是 .
三.解答题
21.已知cos45°=,求cos21°+cos22°+…+cos289°的值.
22.计算:
(1)cos30°+sin45°;
(2)6tan230°﹣sin60°﹣2sin45°.
23.如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,求sinA,cosA,tanA的值.
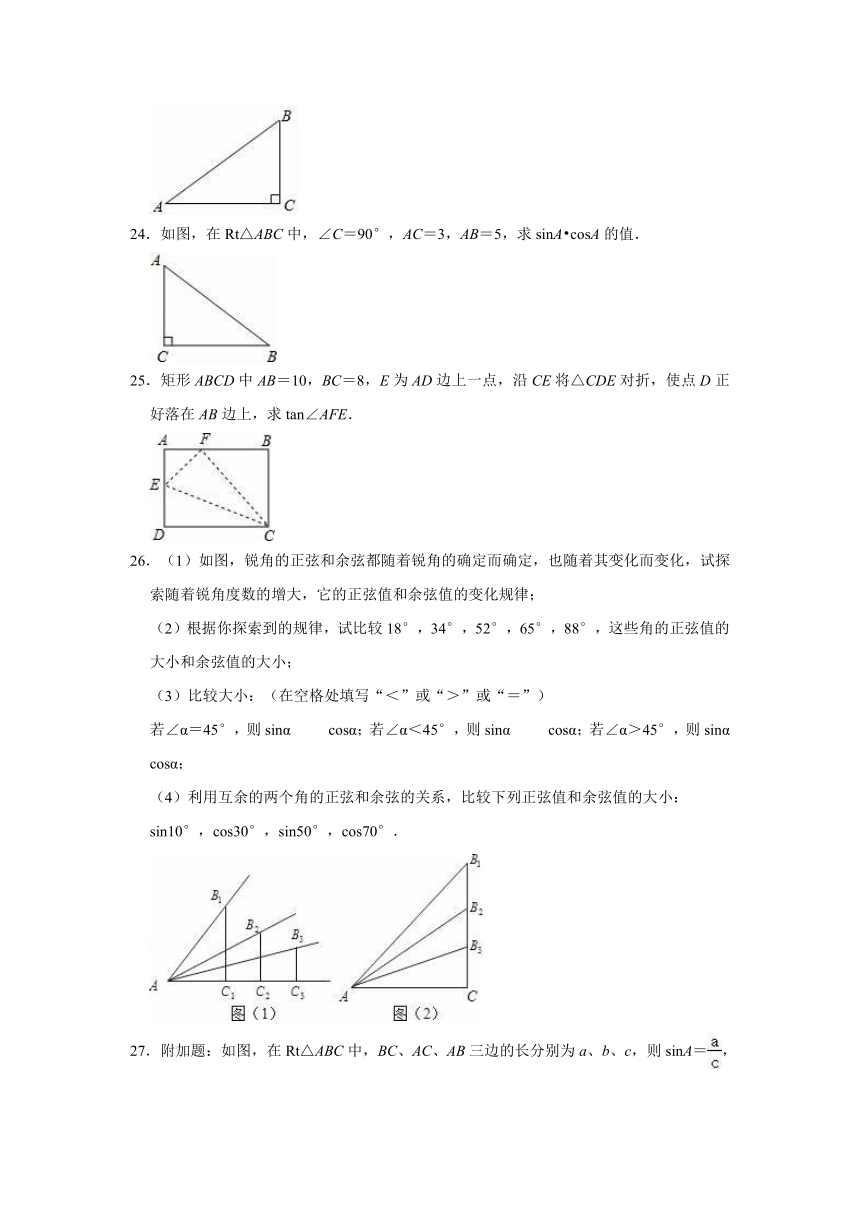
24.如图,在Rt△ABC中,∠C=90°,AC=3,AB=5,求sinA cosA的值.
25.矩形ABCD中AB=10,BC=8,E为AD边上一点,沿CE将△CDE对折,使点D正好落在AB边上,求tan∠AFE.
26.(1)如图,锐角的正弦和余弦都随着锐角的确定而确定,也随着其变化而变化,试探索随着锐角度数的增大,它的正弦值和余弦值的变化规律;
(2)根据你探索到的规律,试比较18°,34°,52°,65°,88°,这些角的正弦值的大小和余弦值的大小;
(3)比较大小:(在空格处填写“<”或“>”或“=”)
若∠α=45°,则sinα cosα;若∠α<45°,则sinα cosα;若∠α>45°,则sinα cosα;
(4)利用互余的两个角的正弦和余弦的关系,比较下列正弦值和余弦值的大小:
sin10°,cos30°,sin50°,cos70°.
27.附加题:如图,在Rt△ABC中,BC、AC、AB三边的长分别为a、b、c,则sinA=,cosA=,tanA=.我们不难发现:sin260°+cos260°=1,…试探求sinA、cosA、tanA之间存在的一般关系,并说明理由.
参考答案与试题解析
一.选择题
1.解:在Rt△ABC中,
∵∠C=90°,AC=3,BC=4,
∴tanA==.
故选:C.
2.解:在Rt△ABC中,∠C=90°,BC=3,AB=5,得cosB==,
故选:D.
3.解:A、若0°<α<90°,则sinα随α的增大而增大,正确;
B、若0°<α<90°,则cosα随α的减小而增大,错误;
C、若0°<α<90°,则tanα随α的增大而增大,正确;
D、0<sinα<1,正确;
故选:B.
4.解:由sinA=知,如果设a=3x,则c=5x,
结合a2+b2=c2得b=4x;
∴tanA===.
故选:C.
5.解:由tan∠B=,得
AC=BC tanB=5×tan26°.
故选:D.
6.解:原式=2×+
=+
=2.
故选:A.
7.解:在Rt△ABC中,∠C=90°,AC=3,BC=4,
由勾股定理,得
AB==5.
cosA==,
故选:A.
8.解:由sinB=,可设∠B的对边是3k,斜边是5k.
则∠B的邻边是4k.
∴tanA==.
故选:D.
9.解:连接AE、EF,如图所示,
则AE∥CD,
∴∠FAE=∠BOD,
∵每个小正方形的边长为1,
则AE==,AF==2,EF==3,
∵()2+(3)2=(2)2,
∴△FAE是直角三角形,∠FEA=90°,
∴sin∠FAE===,
∴sin∠BOD=,
故选:B.
10.解:延长AD、BC,两线交于O,
∵在Rt△ABO中,∠B=90°,tanA==,AB=3,
∴OB=4,
∵BC=2,
∴OC=OB﹣BC=4﹣2=2,
在Rt△ABO中,∠B=90°,AB=3,OB=4,由勾股定理得:AO=5,
∵∠ADC=90°,
∴∠ODC=90°=∠B,
∵∠O=∠O,
∴△ODC∽△OBA,
∴=,
∴=,
解得:DC=,
故选:C.
二.填空题
11.解:∵cosA=,
∴AC=AB cosA=8×=6,
∴BC===2.
故答案是:2.
12.解:∵sin(90°﹣α)=0.625,
∴cosα=0.625.
13.解:由题意得,tan(α+10°)=,
又∵tan30°=,
∴α+10°=30°,
解得:α=20°.
故答案为:20°.
14.解:用科学计算器计算:
373cos81°23'
≈50653×0.1498
≈7588.
故答案为:7588.
15.解:如图所示:∵∠C=90°,AB=6,cosB=,
∴cosB===,
解得:BC=4.
故答案为:4.
16.解:
设小正方形的边长为1,
过C作CF⊥AB于F,
由勾股定理得:AB==2,AC==2,BC=2,
由三角形面积公式得:AB×CF=BC×AE,
2×CF=2×2,
解得:CF=,
在Rt△AFC中,由勾股定理得:AF==
tan∠BAC===,
故答案为:.
17.解:∵cos30°=,余弦函数随角增大而减小,
∴0°<∠A<30°.
18.解:由图可知,AC2=22+42=20,BC2=12+22=5,AB2=32+42=25,
∴△ABC是直角三角形,且∠ACB=90°,
∴cos∠ABC=,
故答案为:.
19.解:由①得 asinθ+bcosθ=c,
两边平方,a2sin2θ+b2cos2θ+2absinθcosθ=c2③
由②得 acosθ﹣bsinθ=﹣d,
两边平方,a2cos2θ+b2sin2θ﹣2absinθcosθ=d2④
③+④得
a2(sin2θ+cos2θ)+b2(sin2θ+cos2θ)=c2+d2
∴a2+b2=c2+d2.
故答案为:a2+b2=c2+d2.
20.解:设直线AB交CE于点H,BD交CE于点N,
设∠E=α,则cos∠E==cosα,则sinα=,tanα=4,
∵tan∠ABD=,则tan∠BHN=2,
∵AE⊥AC,BC⊥AC,
∴AE∥BC,
∴∠E=∠ECB=α,
∵∠NDC+∠NCD=90°,∠NCB+∠NCD=90°,
∴∠NCB=∠NDC=α,
在△AHE中,设AE=a,则AG=AEsinα=asinα,GE=acosα,
则GH===AG=asinα,则EH=GE+GH=acosα+asinα,
在Rt△AEC中,EC==,
则HC=EC﹣EH=﹣(acosα+asinα);
在△BHC中,tan∠BHN=2,tanα=4,HC=﹣(acosα+asinα),
同理可得:BC=×,
在Rt△BCD中,CD==×=a(﹣﹣)=,
AD=AC﹣CD=4a﹣=,
则=,
故答案为.
三.解答题
21.解:原式=(cos21°+cos289°)+(cos22°+cos288°)+…+(cos244°+cos246°)+cos245
=(sin21°+cos21°)+(sin22°+cos22°)+…+(sin244°+cos244°)+cos245
=44+()2
=44.
22.解:(1)把cos30°=,sin45°=,代入得:原式=×+×=;
(2)tan30°=,sin60°=,sin45°=代入得:原式=6×﹣×﹣2×=﹣.
23.解:由勾股定理得,AB===10,
所以sinA==,cosA==,tanA==,
答:sinA=,cosA=,tanA=.
24.解:在Rt△ABC中,∠C=90°,AC=3,AB=5,
由勾股定理得,BC===4,
所以sinA==,cosA==,
所以sinA cosA=×=.
答:sinA cosA的值为.
25.解:根据图形有:∠AFE+∠EFC+∠BFC=180°,
根据折叠的性质,∠EFC=∠EDC=90°,
即∠AFE+∠BFC=90°,
而Rt△BCF中,有∠BCF+∠BFC=90°,
易得∠AFE=∠BCF,
在Rt△BFC,
根据折叠的性质,有CF=CD,
在Rt△BFC中,BC=8,CF=CD=10,
由勾股定理易得:BF=6,
则tan∠BCF=;
故有tan∠AFE=tan∠BCF=;
答:tan∠AFE=.
26.解:(1)在图(1)中,令AB1=AB2=AB3,B1C1⊥AC于点C1,B2C2⊥AC于点C2,B3C3⊥AC于点C3,
显然有:B1C1>B2C2>B3C3,∠B1AC>∠B2AC>∠B3AC.
∵sin∠B1AC=,sin∠B2AC=,sin∠B3AC=,
而>>.
∴sin∠B1AC>sin∠B2AC>sin∠B3AC.
在图(2)中,Rt△ACB3中,∠C=90°,
cos∠B1AC=,cos∠B2AC=,cos∠B3AC=,
∵AB3<AB2<AB1,
∴>>.
即cos∠B3AC>cos∠B2AC>cos∠B1AC.
(2)sin88°>sin65°>sin52°>sin34°>sin18°;
cos88°<cos65°<cos52°<cos34°<cos18°.
(3)若∠α=45°,则sinα=cosα;若∠α<45°,则sinα<cosα;若∠α>45°,则sinα>cosα.
(4)cos30°>sin50°>cos70°>sin10°.
27.解:存在的一般关系有:
(1)sin2A+cos2A=1;
(2)tanA=.
证明:(1)∵sinA=,cosA=,
a2+b2=c2,
∴sin2A+cos2A==1.
(2)∵sinA=,cosA=,
∴tanA==,
=.
一.选择题
1.在△ABC中,∠C=90°,AC=3,BC=4,则tanA的值为( )
A. B. C. D.
2.在Rt△ABC中,∠C=90°,BC=3,AB=5,则cosB的值等于( )
A. B. C. D.
3.若0°<α<90°,则下列说法不正确的是( )
A.sinα随α的增大而增大 B.cosα随α的减小而减小
C.tanα随α的增大而增大 D.0<sinα<1
4.在△ABC中,∠C=90°,sinA=,则tanA=( )
A. B. C. D.
5.如图,在△ABC中,∠ACB=90°,∠ABC=26°,BC=5.若用科学计算器求边AC的长,则下列按键顺序正确的是( )
A.5÷tan26°= B.5÷sin26°= C.5×cos26°= D.5×tan26°=
6.等于( )
A. B.2 C.3 D.
7.如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,则cosA的值为( )
A. B. C. D.
8.已知:Rt△ABC中,∠C=90°,sinB=,则tanA等于( )
A. B. C. D.
9.如图,在正方形方格纸中,每个小方格边长为1,A,B,C,D都在格点处,AB与CD相交于点O,则sin∠BOD的值等于( )
A. B. C. D.
10.如图,在四边形ABCD中,∠B=∠D=90°,AB=3,BC=2,tanA=,则CD的值为( )
A. B. C. D.2
二.填空题
11.△ABC中,∠C=90°,AB=8,cosA=,则BC的长 .
12.已知α为锐角,sin(90°﹣α)=0.625,则cosα= .
13.若,则锐角α= .
14.用科学计算器计算:373cos81°23'≈ .(结果精确到1)
15.在Rt△ABC中,∠C=90°,AB=6,cosB=,则BC的长为 .
16.如图,△ABC的顶点都是正方形网格中的格点,则tan∠BAC等于 .
17.若∠A是锐角,cosA>,则∠A应满足 .
18.如图,在4×4的正方形方格图形中,小正方形的顶点称为格点,△ABC的顶点都在格点上,则图中cos∠ABC= .
19.已知:实常数a、b、c、d同时满足下列两个等式:①asinθ+bcosθ﹣c=0;②acosθ﹣bsinθ+d=0(其中θ为任意锐角),则a、b、c、d之间的关系式是: .
20.在Rt△ABC中,∠ACB=90°,点D是AC边上一点,连BD,过C点作BD的垂线与过A点作AC的垂线交于点E.当tan∠ABD=,cos∠E=,则的值是 .
三.解答题
21.已知cos45°=,求cos21°+cos22°+…+cos289°的值.
22.计算:
(1)cos30°+sin45°;
(2)6tan230°﹣sin60°﹣2sin45°.
23.如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,求sinA,cosA,tanA的值.
24.如图,在Rt△ABC中,∠C=90°,AC=3,AB=5,求sinA cosA的值.
25.矩形ABCD中AB=10,BC=8,E为AD边上一点,沿CE将△CDE对折,使点D正好落在AB边上,求tan∠AFE.
26.(1)如图,锐角的正弦和余弦都随着锐角的确定而确定,也随着其变化而变化,试探索随着锐角度数的增大,它的正弦值和余弦值的变化规律;
(2)根据你探索到的规律,试比较18°,34°,52°,65°,88°,这些角的正弦值的大小和余弦值的大小;
(3)比较大小:(在空格处填写“<”或“>”或“=”)
若∠α=45°,则sinα cosα;若∠α<45°,则sinα cosα;若∠α>45°,则sinα cosα;
(4)利用互余的两个角的正弦和余弦的关系,比较下列正弦值和余弦值的大小:
sin10°,cos30°,sin50°,cos70°.
27.附加题:如图,在Rt△ABC中,BC、AC、AB三边的长分别为a、b、c,则sinA=,cosA=,tanA=.我们不难发现:sin260°+cos260°=1,…试探求sinA、cosA、tanA之间存在的一般关系,并说明理由.
参考答案与试题解析
一.选择题
1.解:在Rt△ABC中,
∵∠C=90°,AC=3,BC=4,
∴tanA==.
故选:C.
2.解:在Rt△ABC中,∠C=90°,BC=3,AB=5,得cosB==,
故选:D.
3.解:A、若0°<α<90°,则sinα随α的增大而增大,正确;
B、若0°<α<90°,则cosα随α的减小而增大,错误;
C、若0°<α<90°,则tanα随α的增大而增大,正确;
D、0<sinα<1,正确;
故选:B.
4.解:由sinA=知,如果设a=3x,则c=5x,
结合a2+b2=c2得b=4x;
∴tanA===.
故选:C.
5.解:由tan∠B=,得
AC=BC tanB=5×tan26°.
故选:D.
6.解:原式=2×+
=+
=2.
故选:A.
7.解:在Rt△ABC中,∠C=90°,AC=3,BC=4,
由勾股定理,得
AB==5.
cosA==,
故选:A.
8.解:由sinB=,可设∠B的对边是3k,斜边是5k.
则∠B的邻边是4k.
∴tanA==.
故选:D.
9.解:连接AE、EF,如图所示,
则AE∥CD,
∴∠FAE=∠BOD,
∵每个小正方形的边长为1,
则AE==,AF==2,EF==3,
∵()2+(3)2=(2)2,
∴△FAE是直角三角形,∠FEA=90°,
∴sin∠FAE===,
∴sin∠BOD=,
故选:B.
10.解:延长AD、BC,两线交于O,
∵在Rt△ABO中,∠B=90°,tanA==,AB=3,
∴OB=4,
∵BC=2,
∴OC=OB﹣BC=4﹣2=2,
在Rt△ABO中,∠B=90°,AB=3,OB=4,由勾股定理得:AO=5,
∵∠ADC=90°,
∴∠ODC=90°=∠B,
∵∠O=∠O,
∴△ODC∽△OBA,
∴=,
∴=,
解得:DC=,
故选:C.
二.填空题
11.解:∵cosA=,
∴AC=AB cosA=8×=6,
∴BC===2.
故答案是:2.
12.解:∵sin(90°﹣α)=0.625,
∴cosα=0.625.
13.解:由题意得,tan(α+10°)=,
又∵tan30°=,
∴α+10°=30°,
解得:α=20°.
故答案为:20°.
14.解:用科学计算器计算:
373cos81°23'
≈50653×0.1498
≈7588.
故答案为:7588.
15.解:如图所示:∵∠C=90°,AB=6,cosB=,
∴cosB===,
解得:BC=4.
故答案为:4.
16.解:
设小正方形的边长为1,
过C作CF⊥AB于F,
由勾股定理得:AB==2,AC==2,BC=2,
由三角形面积公式得:AB×CF=BC×AE,
2×CF=2×2,
解得:CF=,
在Rt△AFC中,由勾股定理得:AF==
tan∠BAC===,
故答案为:.
17.解:∵cos30°=,余弦函数随角增大而减小,
∴0°<∠A<30°.
18.解:由图可知,AC2=22+42=20,BC2=12+22=5,AB2=32+42=25,
∴△ABC是直角三角形,且∠ACB=90°,
∴cos∠ABC=,
故答案为:.
19.解:由①得 asinθ+bcosθ=c,
两边平方,a2sin2θ+b2cos2θ+2absinθcosθ=c2③
由②得 acosθ﹣bsinθ=﹣d,
两边平方,a2cos2θ+b2sin2θ﹣2absinθcosθ=d2④
③+④得
a2(sin2θ+cos2θ)+b2(sin2θ+cos2θ)=c2+d2
∴a2+b2=c2+d2.
故答案为:a2+b2=c2+d2.
20.解:设直线AB交CE于点H,BD交CE于点N,
设∠E=α,则cos∠E==cosα,则sinα=,tanα=4,
∵tan∠ABD=,则tan∠BHN=2,
∵AE⊥AC,BC⊥AC,
∴AE∥BC,
∴∠E=∠ECB=α,
∵∠NDC+∠NCD=90°,∠NCB+∠NCD=90°,
∴∠NCB=∠NDC=α,
在△AHE中,设AE=a,则AG=AEsinα=asinα,GE=acosα,
则GH===AG=asinα,则EH=GE+GH=acosα+asinα,
在Rt△AEC中,EC==,
则HC=EC﹣EH=﹣(acosα+asinα);
在△BHC中,tan∠BHN=2,tanα=4,HC=﹣(acosα+asinα),
同理可得:BC=×,
在Rt△BCD中,CD==×=a(﹣﹣)=,
AD=AC﹣CD=4a﹣=,
则=,
故答案为.
三.解答题
21.解:原式=(cos21°+cos289°)+(cos22°+cos288°)+…+(cos244°+cos246°)+cos245
=(sin21°+cos21°)+(sin22°+cos22°)+…+(sin244°+cos244°)+cos245
=44+()2
=44.
22.解:(1)把cos30°=,sin45°=,代入得:原式=×+×=;
(2)tan30°=,sin60°=,sin45°=代入得:原式=6×﹣×﹣2×=﹣.
23.解:由勾股定理得,AB===10,
所以sinA==,cosA==,tanA==,
答:sinA=,cosA=,tanA=.
24.解:在Rt△ABC中,∠C=90°,AC=3,AB=5,
由勾股定理得,BC===4,
所以sinA==,cosA==,
所以sinA cosA=×=.
答:sinA cosA的值为.
25.解:根据图形有:∠AFE+∠EFC+∠BFC=180°,
根据折叠的性质,∠EFC=∠EDC=90°,
即∠AFE+∠BFC=90°,
而Rt△BCF中,有∠BCF+∠BFC=90°,
易得∠AFE=∠BCF,
在Rt△BFC,
根据折叠的性质,有CF=CD,
在Rt△BFC中,BC=8,CF=CD=10,
由勾股定理易得:BF=6,
则tan∠BCF=;
故有tan∠AFE=tan∠BCF=;
答:tan∠AFE=.
26.解:(1)在图(1)中,令AB1=AB2=AB3,B1C1⊥AC于点C1,B2C2⊥AC于点C2,B3C3⊥AC于点C3,
显然有:B1C1>B2C2>B3C3,∠B1AC>∠B2AC>∠B3AC.
∵sin∠B1AC=,sin∠B2AC=,sin∠B3AC=,
而>>.
∴sin∠B1AC>sin∠B2AC>sin∠B3AC.
在图(2)中,Rt△ACB3中,∠C=90°,
cos∠B1AC=,cos∠B2AC=,cos∠B3AC=,
∵AB3<AB2<AB1,
∴>>.
即cos∠B3AC>cos∠B2AC>cos∠B1AC.
(2)sin88°>sin65°>sin52°>sin34°>sin18°;
cos88°<cos65°<cos52°<cos34°<cos18°.
(3)若∠α=45°,则sinα=cosα;若∠α<45°,则sinα<cosα;若∠α>45°,则sinα>cosα.
(4)cos30°>sin50°>cos70°>sin10°.
27.解:存在的一般关系有:
(1)sin2A+cos2A=1;
(2)tanA=.
证明:(1)∵sinA=,cosA=,
a2+b2=c2,
∴sin2A+cos2A==1.
(2)∵sinA=,cosA=,
∴tanA==,
=.
