沪科新版2021-2022学年七年级上册数学《第4章 直线与角》单元测试卷(word版含解析)
文档属性
| 名称 | 沪科新版2021-2022学年七年级上册数学《第4章 直线与角》单元测试卷(word版含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 196.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-26 16:10:06 | ||
图片预览

文档简介
2021-2022学年沪科新版七年级上册数学《第4章 直线与角》单元测试卷
一.选择题
1.下列说法正确的是( )
A.有六条侧棱的棱柱的底面一定是三角形
B.棱锥的侧面是三角形
C.长方体和正方体不是棱柱
D.柱体的上、下两底面可以大小不一样
2.与图中实物图相类似的立体图形按从左至右的顺序依次是( )
A.圆柱、圆锥、正方体、长方体
B.圆柱、球、正方体、长方体
C.棱柱、球、正方体、棱柱
D.棱柱、圆锥、棱柱、长方体
3.由5个棱长为1的小正方体组成的几何体如图放置,一面着地,两面靠墙.如果要将露出来的部分涂色,则涂色部分的面积为( )
A.9 B.11 C.14 D.18
4.若圆的半径由3厘米增加到15厘米,则圆的周长增加了( )
A.4厘米 B.2π厘米 C.24π厘米 D.16π厘米
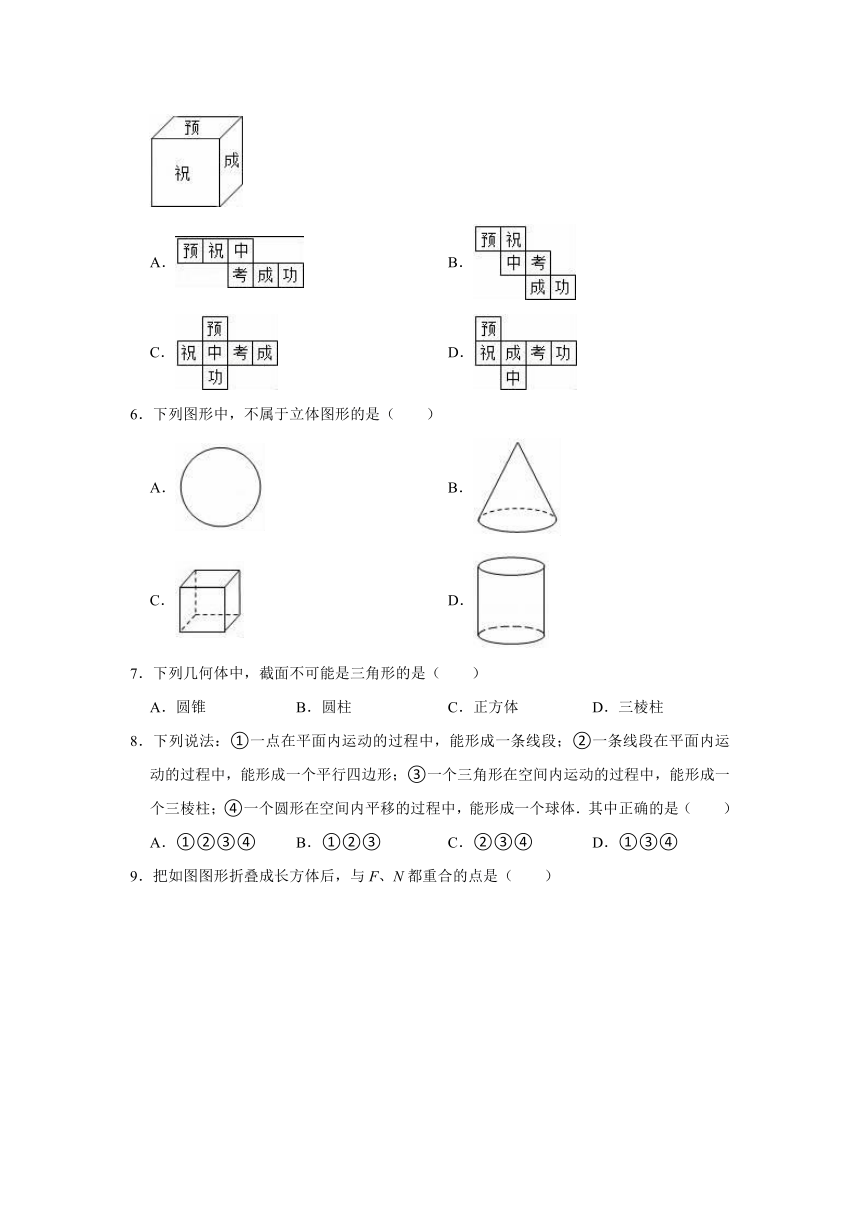
5.妈妈为今年参加中考的女儿小红制作了一个正方体礼品盒(如图),六个面上各有一个字,连起来就是“预祝中考成功”,其中“祝”的对面是“考”,“成”的对面是“功”,则它的平面展开图可能是( )
A. B.
C. D.
6.下列图形中,不属于立体图形的是( )
A. B.
C. D.
7.下列几何体中,截面不可能是三角形的是( )
A.圆锥 B.圆柱 C.正方体 D.三棱柱
8.下列说法:①一点在平面内运动的过程中,能形成一条线段;②一条线段在平面内运动的过程中,能形成一个平行四边形;③一个三角形在空间内运动的过程中,能形成一个三棱柱;④一个圆形在空间内平移的过程中,能形成一个球体.其中正确的是( )
A.①②③④ B.①②③ C.②③④ D.①③④
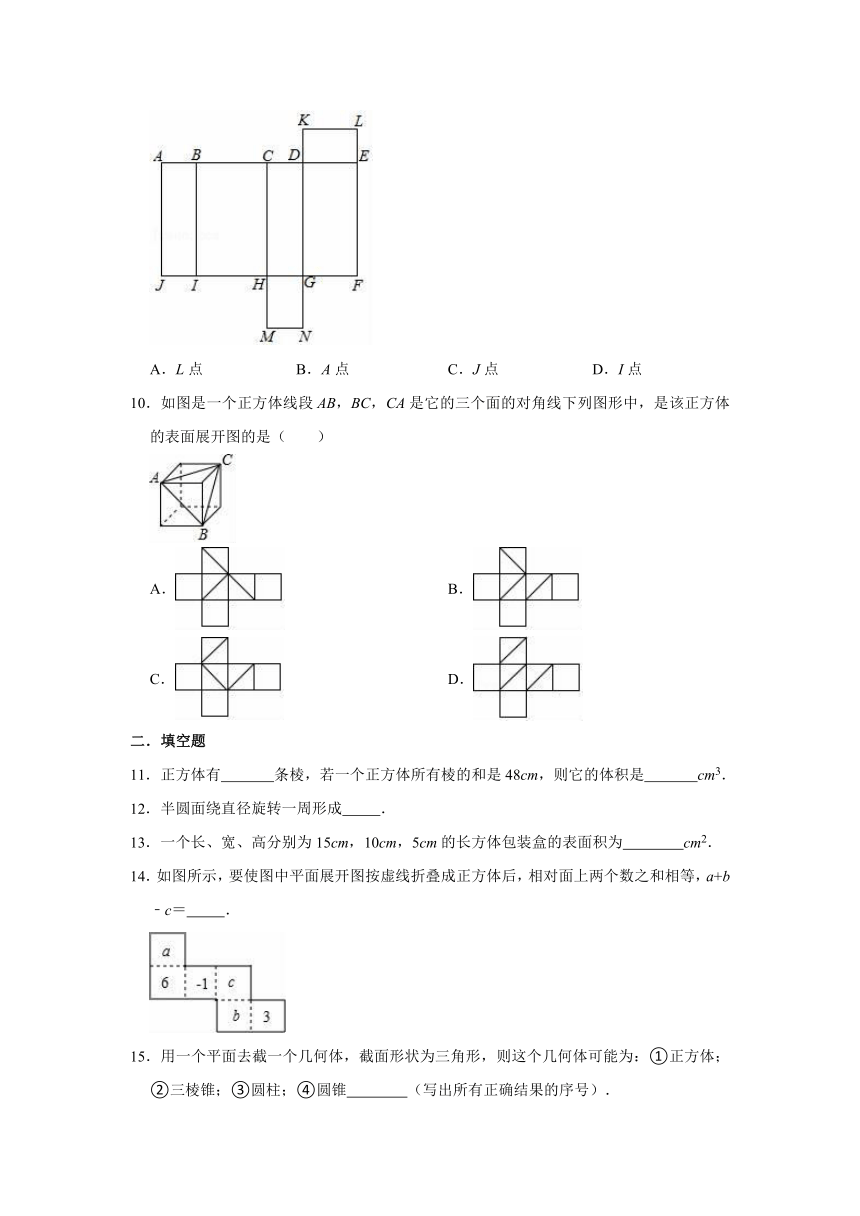
9.把如图图形折叠成长方体后,与F、N都重合的点是( )
A.L点 B.A点 C.J点 D.I点
10.如图是一个正方体线段AB,BC,CA是它的三个面的对角线下列图形中,是该正方体的表面展开图的是( )
A. B.
C. D.
二.填空题
11.正方体有 条棱,若一个正方体所有棱的和是48cm,则它的体积是 cm3.
12.半圆面绕直径旋转一周形成 .
13.一个长、宽、高分别为15cm,10cm,5cm的长方体包装盒的表面积为 cm2.
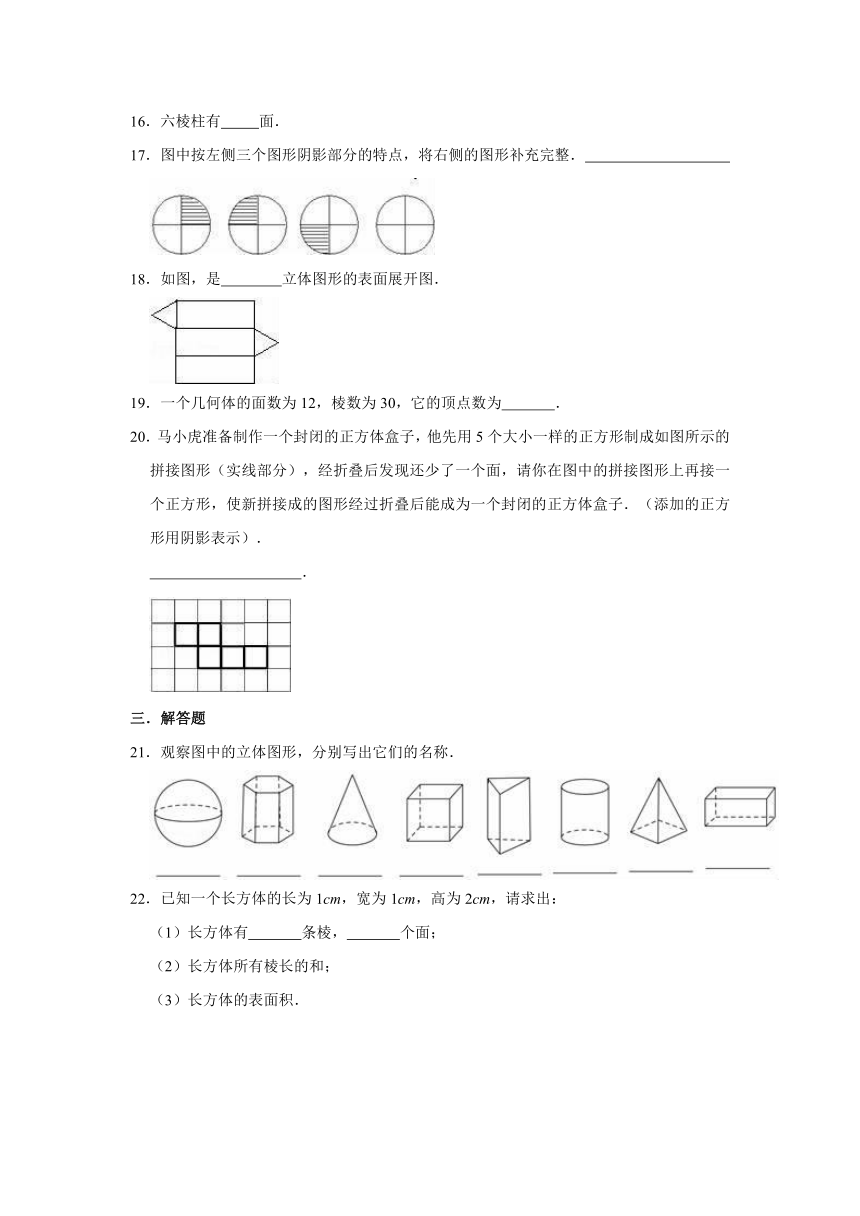
14.如图所示,要使图中平面展开图按虚线折叠成正方体后,相对面上两个数之和相等,a+b﹣c= .
15.用一个平面去截一个几何体,截面形状为三角形,则这个几何体可能为:①正方体;②三棱锥;③圆柱;④圆锥 (写出所有正确结果的序号).
16.六棱柱有 面.
17.图中按左侧三个图形阴影部分的特点,将右侧的图形补充完整.
18.如图,是 立体图形的表面展开图.
19.一个几何体的面数为12,棱数为30,它的顶点数为 .
20.马小虎准备制作一个封闭的正方体盒子,他先用5个大小一样的正方形制成如图所示的拼接图形(实线部分),经折叠后发现还少了一个面,请你在图中的拼接图形上再接一个正方形,使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子.(添加的正方形用阴影表示).
.
三.解答题
21.观察图中的立体图形,分别写出它们的名称.
22.已知一个长方体的长为1cm,宽为1cm,高为2cm,请求出:
(1)长方体有 条棱, 个面;
(2)长方体所有棱长的和;
(3)长方体的表面积.
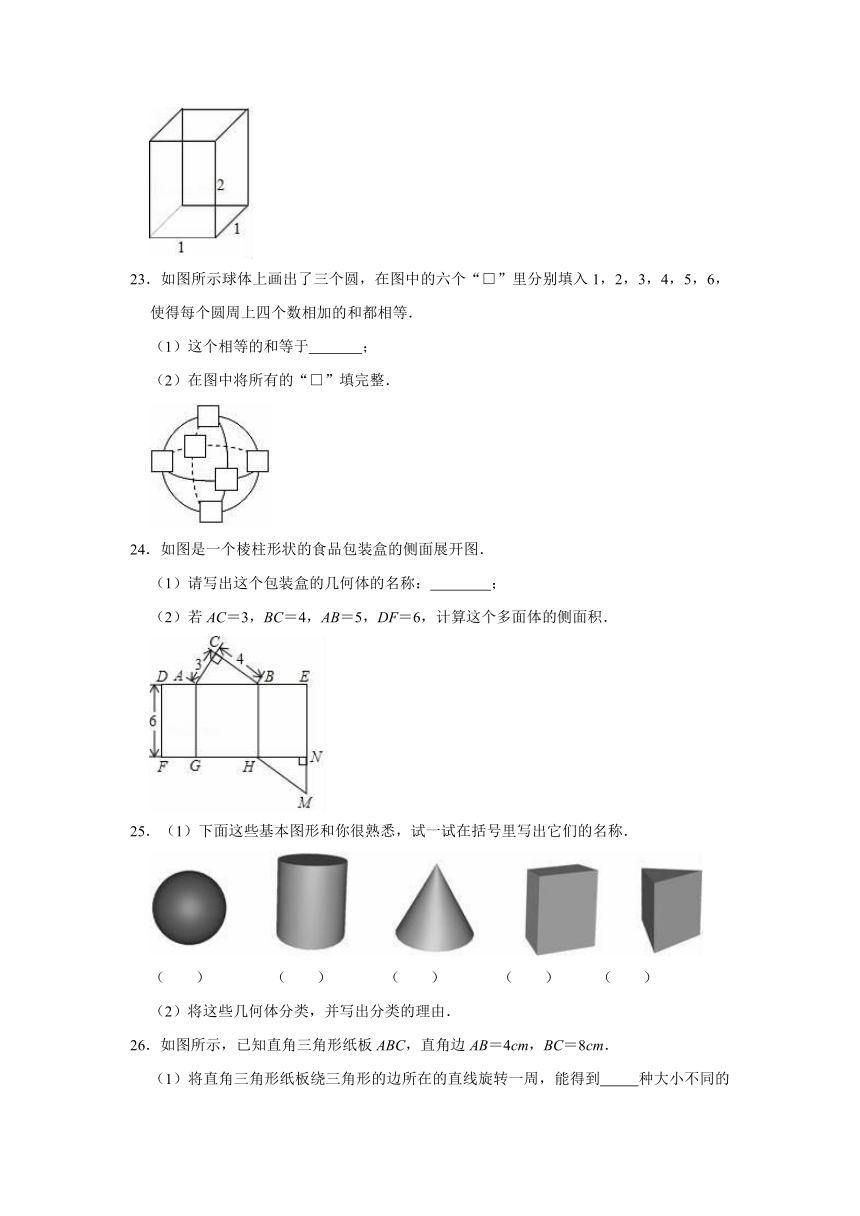
23.如图所示球体上画出了三个圆,在图中的六个“□”里分别填入1,2,3,4,5,6,使得每个圆周上四个数相加的和都相等.
(1)这个相等的和等于 ;
(2)在图中将所有的“□”填完整.
24.如图是一个棱柱形状的食品包装盒的侧面展开图.
(1)请写出这个包装盒的几何体的名称: ;
(2)若AC=3,BC=4,AB=5,DF=6,计算这个多面体的侧面积.
25.(1)下面这些基本图形和你很熟悉,试一试在括号里写出它们的名称.
( ) ( ) ( ) ( ) ( )
(2)将这些几何体分类,并写出分类的理由.
26.如图所示,已知直角三角形纸板ABC,直角边AB=4cm,BC=8cm.
(1)将直角三角形纸板绕三角形的边所在的直线旋转一周,能得到 种大小不同的几何体?
(2)分别计算绕三角形直角边所在的直线旋转一周,得到的几何体的体积?(圆锥的体积=πr2h,其中π取3)
27.随着城市的发展,住宅小区的建设也越来越人性化.为响应国家“加强全民健身设施建设,发展全民体育”的号召.哈市某小区在一片足够大的空地中,改建出一个休闲广场,规划设计如图所示.(π取3)
(1)求塑胶地面休闲区的面积;
(2)求广场中种植花卉的面积与种植草坪的面积的比值.
参考答案与试题解析
一.选择题
1.解:A、有六条侧棱的棱柱的底面是六边形,故本选项错误;
B、符合棱锥的定义,故本选项正确;
C、长方体和正方体是棱柱,故本选项错误;
D、柱体的上、下两底面大小一样,故本选项错误.
故选:B.
2.解:与图中实物图相类似的立体图形按从左至右的顺序依次是圆柱、球、正方体、长方体.
故选:B.
3.解:由图可知涂色部分是从上、前、右三个方向所涂面积相加,即涂色部分面积为4+4+3=11,
故选:B.
4.解:圆的周长增加了:2π×(15﹣3)=24π(厘米).
故选:C.
5.解:A、“祝”的对面是“成”,故本选项错误;
B、“祝”的对面是“成”,故本选项错误;
C、三个汉字的位置不对应,故本选项错误;
D、符合,故本选项正确.
故选:D.
6.解:圆是平面图形,不是立体图形,圆锥体、圆柱体、正方体都是立体图形,
故选:A.
7.解:A、过圆锥的顶点和下底圆心的面得到的截面是三角形,不符合题意;
B、圆柱的截面跟圆、四边形有关,符合题意;
C、过正方体的三个面得到的截面是三角形,不符合题意;
D、过三棱柱的三个面得到的截面是三角形,不符合题意.
故选:B.
8.解:①一点在平面内运动的过程中,能形成一条线段是正确的;
②一条线段在平面内运动的过程中,能形成一个平行四边形是正确的;
③一个三角形在空间内运动的过程中,能形成一个三棱柱是正确的;
④一个圆形在空间内平移的过程中,能形成一个圆柱,原来的说法错误.
故选:B.
9.解:观察图形可知,把图形折叠成长方体后,与F、N都重合的点是J点.
故选:C.
10.解:根据正方体展开图的特点分析,选项C是它的展开图.
故选:C.
二.填空题
11.解:正方体有12条棱,
当正方体所有棱的和是48cm,则它的棱长为48÷12=4(cm),
它的体积是4×4×4=64(cm3),
故答案为:64.
12.解:半圆绕它的直径旋转360度形成球.
故答案为球
13.解:长方体的表面积是:2×(15×10+15×5+10×5)=550cm2.
答案:550.
14.解:正方体的表面展开图,相对的面之间一定相隔一个正方形,
∴a与b是相对面,
6与c是相对面,
﹣1与3是相对面,
∵相对面上两个数之和相等,
∴a+b=﹣1+3,6+c=﹣1+3,
解得a+b=2,c=﹣4,
∴a+b﹣c=2﹣(﹣4)=6.
故答案为:6.
15.解:①正方体能截出三角形;
②三棱锥能截出三角形;
③圆柱不能截出三角形;
④圆锥沿着母线截几何体可以截出三角形.
故截面可能是三角形的有3个.
故答案为:①②④
16.解:六棱柱上下两个底面,侧面是6个长方形,所以共有8个面.
故答案为:8.
17.解:观察图形可知,阴影部分是逆时针转动的,所以右侧的图形是.
故答案为.
18.解:三棱柱能展成如图所示的平面图形.
19.解:∵简单多面体的顶点数V、面数F及棱数E间的关系为:V+F﹣E=2,一个棱柱的面数为12,棱数是30,
∴则其顶点数为:V+12﹣30=2,
解得:V=20.
故答案为:20
20.解:不止一种,仅供参考.
三.解答题
21.解:它们的名称分别为:球体,直六棱柱,圆锥体,正方体,直三棱柱,圆柱体,四棱锥,长方体.
22.解:(1)长方体有12条棱,6个面;
故答案为:12,6;
(2)(1+1+2)×4
=4×4
=16(cm).
故长方体所有棱长的和是16cm;
(3)(1×1+1×2+1×2)×2
=(1+2+2)×2
=5×2
=10(cm2).
故长方体的表面积是10cm2.
23.解:(1)(1+2+3+4+5+6)×2÷3
=21×2÷3
=14;
(2)如图所示:
故答案为:14.
24.解:(1)共有3个长方形组成侧面,2个三角形组成底面,故是三棱柱;
故答案为:三棱柱;
(2)∵AB=5,AD=3,BE=4,DF=6
∴侧面积为3×6+5×6+4×6=18+30+24=72.
25.解:(1)从左向右依次是:球、圆柱、圆锥、长方体、三棱柱.
(2)观察图形,按柱、锥、球划分,则有圆柱、长方体、三棱柱为柱体;圆锥为锥体;球为球体.
26.解:(1)将直角三角形纸板ABC绕三角形的三条边所在的直线旋转一周,能得到3种大小不同的几何体.
故答案为:3.
(2)以AB为轴:
×3×82×4
=×3×64×4
=256(立方厘米);
以BC为轴:
×3×42×8
=×3×16×8
=128(立方厘米).
答:以AB为轴得到的圆锥的体积是256立方厘米,以BC为轴得到的圆锥的体积是128立方厘米.
27.解:(1)S塑胶地面=S长方形+S半圆=10×20+π×()2=200+50π≈350(平方米),
答:塑胶地面休闲区的面积为350平方米;
(2)S种花卉=S长方形﹣S半圆=200﹣150=50(平方米),
S种草坪=S半圆=50π≈150(平方米),
所以,广场中种植花卉的面积与种植草坪的面积的比值为=.
一.选择题
1.下列说法正确的是( )
A.有六条侧棱的棱柱的底面一定是三角形
B.棱锥的侧面是三角形
C.长方体和正方体不是棱柱
D.柱体的上、下两底面可以大小不一样
2.与图中实物图相类似的立体图形按从左至右的顺序依次是( )
A.圆柱、圆锥、正方体、长方体
B.圆柱、球、正方体、长方体
C.棱柱、球、正方体、棱柱
D.棱柱、圆锥、棱柱、长方体
3.由5个棱长为1的小正方体组成的几何体如图放置,一面着地,两面靠墙.如果要将露出来的部分涂色,则涂色部分的面积为( )
A.9 B.11 C.14 D.18
4.若圆的半径由3厘米增加到15厘米,则圆的周长增加了( )
A.4厘米 B.2π厘米 C.24π厘米 D.16π厘米
5.妈妈为今年参加中考的女儿小红制作了一个正方体礼品盒(如图),六个面上各有一个字,连起来就是“预祝中考成功”,其中“祝”的对面是“考”,“成”的对面是“功”,则它的平面展开图可能是( )
A. B.
C. D.
6.下列图形中,不属于立体图形的是( )
A. B.
C. D.
7.下列几何体中,截面不可能是三角形的是( )
A.圆锥 B.圆柱 C.正方体 D.三棱柱
8.下列说法:①一点在平面内运动的过程中,能形成一条线段;②一条线段在平面内运动的过程中,能形成一个平行四边形;③一个三角形在空间内运动的过程中,能形成一个三棱柱;④一个圆形在空间内平移的过程中,能形成一个球体.其中正确的是( )
A.①②③④ B.①②③ C.②③④ D.①③④
9.把如图图形折叠成长方体后,与F、N都重合的点是( )
A.L点 B.A点 C.J点 D.I点
10.如图是一个正方体线段AB,BC,CA是它的三个面的对角线下列图形中,是该正方体的表面展开图的是( )
A. B.
C. D.
二.填空题
11.正方体有 条棱,若一个正方体所有棱的和是48cm,则它的体积是 cm3.
12.半圆面绕直径旋转一周形成 .
13.一个长、宽、高分别为15cm,10cm,5cm的长方体包装盒的表面积为 cm2.
14.如图所示,要使图中平面展开图按虚线折叠成正方体后,相对面上两个数之和相等,a+b﹣c= .
15.用一个平面去截一个几何体,截面形状为三角形,则这个几何体可能为:①正方体;②三棱锥;③圆柱;④圆锥 (写出所有正确结果的序号).
16.六棱柱有 面.
17.图中按左侧三个图形阴影部分的特点,将右侧的图形补充完整.
18.如图,是 立体图形的表面展开图.
19.一个几何体的面数为12,棱数为30,它的顶点数为 .
20.马小虎准备制作一个封闭的正方体盒子,他先用5个大小一样的正方形制成如图所示的拼接图形(实线部分),经折叠后发现还少了一个面,请你在图中的拼接图形上再接一个正方形,使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子.(添加的正方形用阴影表示).
.
三.解答题
21.观察图中的立体图形,分别写出它们的名称.
22.已知一个长方体的长为1cm,宽为1cm,高为2cm,请求出:
(1)长方体有 条棱, 个面;
(2)长方体所有棱长的和;
(3)长方体的表面积.
23.如图所示球体上画出了三个圆,在图中的六个“□”里分别填入1,2,3,4,5,6,使得每个圆周上四个数相加的和都相等.
(1)这个相等的和等于 ;
(2)在图中将所有的“□”填完整.
24.如图是一个棱柱形状的食品包装盒的侧面展开图.
(1)请写出这个包装盒的几何体的名称: ;
(2)若AC=3,BC=4,AB=5,DF=6,计算这个多面体的侧面积.
25.(1)下面这些基本图形和你很熟悉,试一试在括号里写出它们的名称.
( ) ( ) ( ) ( ) ( )
(2)将这些几何体分类,并写出分类的理由.
26.如图所示,已知直角三角形纸板ABC,直角边AB=4cm,BC=8cm.
(1)将直角三角形纸板绕三角形的边所在的直线旋转一周,能得到 种大小不同的几何体?
(2)分别计算绕三角形直角边所在的直线旋转一周,得到的几何体的体积?(圆锥的体积=πr2h,其中π取3)
27.随着城市的发展,住宅小区的建设也越来越人性化.为响应国家“加强全民健身设施建设,发展全民体育”的号召.哈市某小区在一片足够大的空地中,改建出一个休闲广场,规划设计如图所示.(π取3)
(1)求塑胶地面休闲区的面积;
(2)求广场中种植花卉的面积与种植草坪的面积的比值.
参考答案与试题解析
一.选择题
1.解:A、有六条侧棱的棱柱的底面是六边形,故本选项错误;
B、符合棱锥的定义,故本选项正确;
C、长方体和正方体是棱柱,故本选项错误;
D、柱体的上、下两底面大小一样,故本选项错误.
故选:B.
2.解:与图中实物图相类似的立体图形按从左至右的顺序依次是圆柱、球、正方体、长方体.
故选:B.
3.解:由图可知涂色部分是从上、前、右三个方向所涂面积相加,即涂色部分面积为4+4+3=11,
故选:B.
4.解:圆的周长增加了:2π×(15﹣3)=24π(厘米).
故选:C.
5.解:A、“祝”的对面是“成”,故本选项错误;
B、“祝”的对面是“成”,故本选项错误;
C、三个汉字的位置不对应,故本选项错误;
D、符合,故本选项正确.
故选:D.
6.解:圆是平面图形,不是立体图形,圆锥体、圆柱体、正方体都是立体图形,
故选:A.
7.解:A、过圆锥的顶点和下底圆心的面得到的截面是三角形,不符合题意;
B、圆柱的截面跟圆、四边形有关,符合题意;
C、过正方体的三个面得到的截面是三角形,不符合题意;
D、过三棱柱的三个面得到的截面是三角形,不符合题意.
故选:B.
8.解:①一点在平面内运动的过程中,能形成一条线段是正确的;
②一条线段在平面内运动的过程中,能形成一个平行四边形是正确的;
③一个三角形在空间内运动的过程中,能形成一个三棱柱是正确的;
④一个圆形在空间内平移的过程中,能形成一个圆柱,原来的说法错误.
故选:B.
9.解:观察图形可知,把图形折叠成长方体后,与F、N都重合的点是J点.
故选:C.
10.解:根据正方体展开图的特点分析,选项C是它的展开图.
故选:C.
二.填空题
11.解:正方体有12条棱,
当正方体所有棱的和是48cm,则它的棱长为48÷12=4(cm),
它的体积是4×4×4=64(cm3),
故答案为:64.
12.解:半圆绕它的直径旋转360度形成球.
故答案为球
13.解:长方体的表面积是:2×(15×10+15×5+10×5)=550cm2.
答案:550.
14.解:正方体的表面展开图,相对的面之间一定相隔一个正方形,
∴a与b是相对面,
6与c是相对面,
﹣1与3是相对面,
∵相对面上两个数之和相等,
∴a+b=﹣1+3,6+c=﹣1+3,
解得a+b=2,c=﹣4,
∴a+b﹣c=2﹣(﹣4)=6.
故答案为:6.
15.解:①正方体能截出三角形;
②三棱锥能截出三角形;
③圆柱不能截出三角形;
④圆锥沿着母线截几何体可以截出三角形.
故截面可能是三角形的有3个.
故答案为:①②④
16.解:六棱柱上下两个底面,侧面是6个长方形,所以共有8个面.
故答案为:8.
17.解:观察图形可知,阴影部分是逆时针转动的,所以右侧的图形是.
故答案为.
18.解:三棱柱能展成如图所示的平面图形.
19.解:∵简单多面体的顶点数V、面数F及棱数E间的关系为:V+F﹣E=2,一个棱柱的面数为12,棱数是30,
∴则其顶点数为:V+12﹣30=2,
解得:V=20.
故答案为:20
20.解:不止一种,仅供参考.
三.解答题
21.解:它们的名称分别为:球体,直六棱柱,圆锥体,正方体,直三棱柱,圆柱体,四棱锥,长方体.
22.解:(1)长方体有12条棱,6个面;
故答案为:12,6;
(2)(1+1+2)×4
=4×4
=16(cm).
故长方体所有棱长的和是16cm;
(3)(1×1+1×2+1×2)×2
=(1+2+2)×2
=5×2
=10(cm2).
故长方体的表面积是10cm2.
23.解:(1)(1+2+3+4+5+6)×2÷3
=21×2÷3
=14;
(2)如图所示:
故答案为:14.
24.解:(1)共有3个长方形组成侧面,2个三角形组成底面,故是三棱柱;
故答案为:三棱柱;
(2)∵AB=5,AD=3,BE=4,DF=6
∴侧面积为3×6+5×6+4×6=18+30+24=72.
25.解:(1)从左向右依次是:球、圆柱、圆锥、长方体、三棱柱.
(2)观察图形,按柱、锥、球划分,则有圆柱、长方体、三棱柱为柱体;圆锥为锥体;球为球体.
26.解:(1)将直角三角形纸板ABC绕三角形的三条边所在的直线旋转一周,能得到3种大小不同的几何体.
故答案为:3.
(2)以AB为轴:
×3×82×4
=×3×64×4
=256(立方厘米);
以BC为轴:
×3×42×8
=×3×16×8
=128(立方厘米).
答:以AB为轴得到的圆锥的体积是256立方厘米,以BC为轴得到的圆锥的体积是128立方厘米.
27.解:(1)S塑胶地面=S长方形+S半圆=10×20+π×()2=200+50π≈350(平方米),
答:塑胶地面休闲区的面积为350平方米;
(2)S种花卉=S长方形﹣S半圆=200﹣150=50(平方米),
S种草坪=S半圆=50π≈150(平方米),
所以,广场中种植花卉的面积与种植草坪的面积的比值为=.
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
