2021-2022学年鲁教五四新版九年级上册数学《第4章 投影与视图》单元测试卷(word版含解析)
文档属性
| 名称 | 2021-2022学年鲁教五四新版九年级上册数学《第4章 投影与视图》单元测试卷(word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 327.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-26 16:52:10 | ||
图片预览



文档简介
2021-2022学年鲁教五四新版九年级上册数学《第4章 投影与视图》单元测试卷
一.选择题
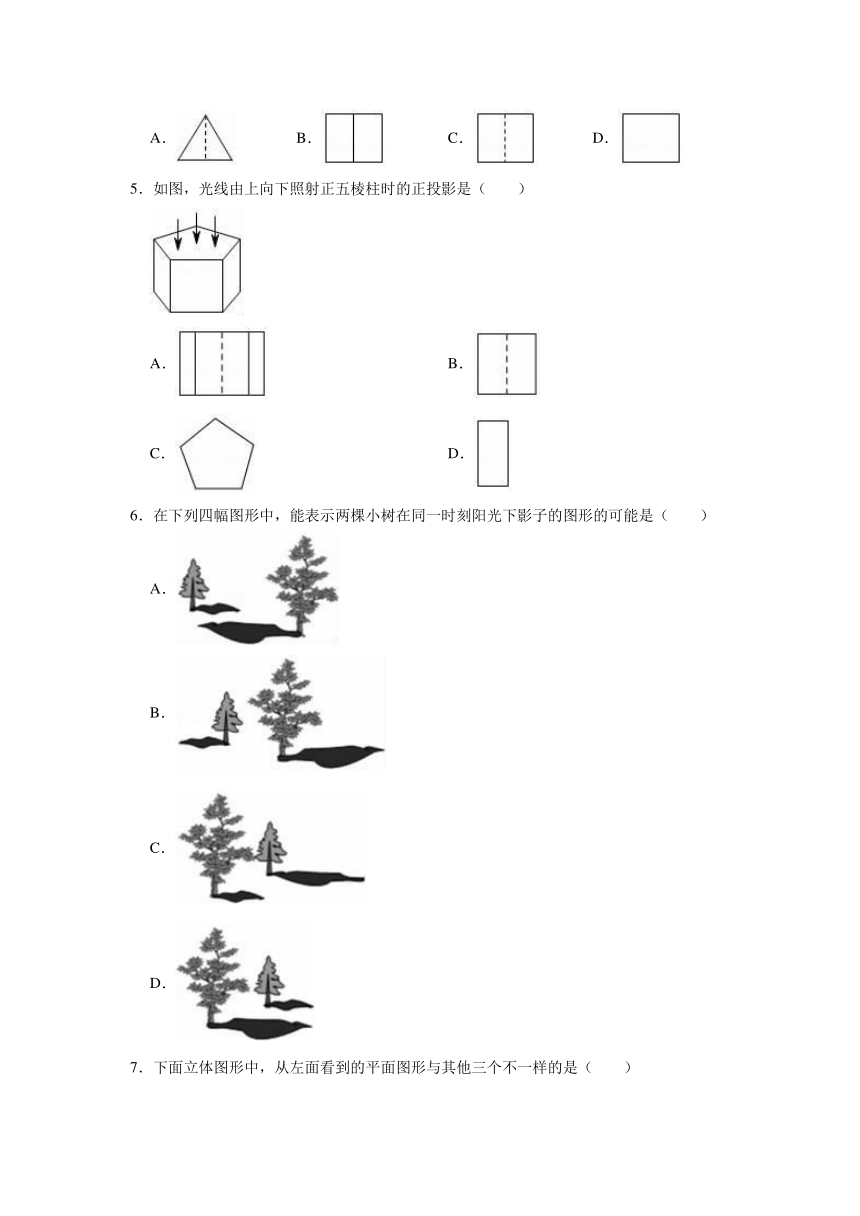
1.如图,晚上小亮在路灯下散步,在小亮由A处径直走到B处这一过程中,他在地上的影子( )
A.逐渐变短 B.先变短后变长
C.先变长后变短 D.逐渐变长
2.如图,在房子屋檐E处安有一台监视器,房子前有一面落地的广告牌,那么监视器的盲区是( )
A.△ACE B.△ADF C.△ABD D.四边形BCED
3.如图,这是一个机械模具,则它的左视图是( )
A. B. C. D.
4.如图所示,该几何体的俯视图是( )
A. B. C. D.
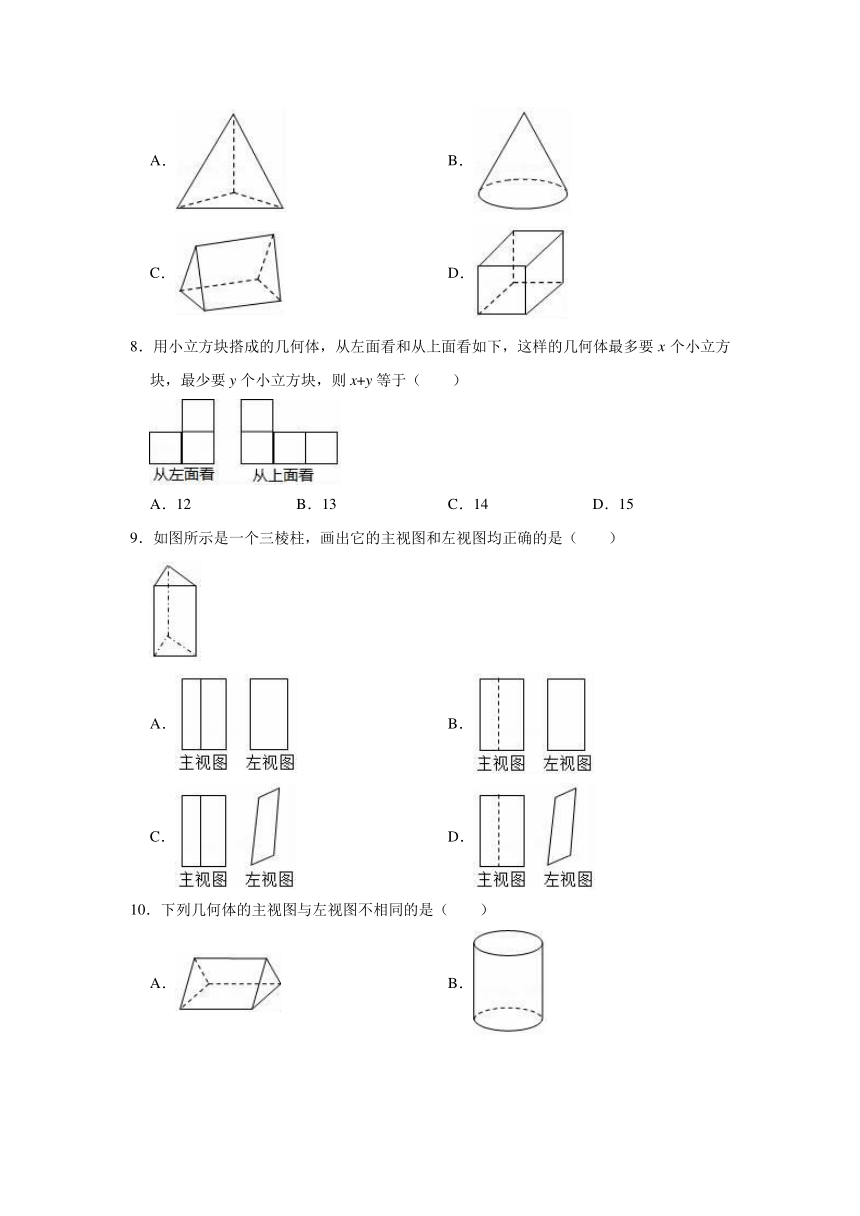
5.如图,光线由上向下照射正五棱柱时的正投影是( )
A. B.
C. D.
6.在下列四幅图形中,能表示两棵小树在同一时刻阳光下影子的图形的可能是( )
A.
B.
C.
D.
7.下面立体图形中,从左面看到的平面图形与其他三个不一样的是( )
A. B.
C. D.
8.用小立方块搭成的几何体,从左面看和从上面看如下,这样的几何体最多要x个小立方块,最少要y个小立方块,则x+y等于( )
A.12 B.13 C.14 D.15
9.如图所示是一个三棱柱,画出它的主视图和左视图均正确的是( )
A. B.
C. D.
10.下列几何体的主视图与左视图不相同的是( )
A. B.
C. D.
二.填空题
11.球的主视图、俯视图、左视图都是 .
12.直角三角形的正投影可能是 .
13.如右图,是一个由若干个小正方体搭建而成的几何体的主视图与左视图,那么下列图形中可以作为该几何体的俯视图的序号是 (多填或错填得0分,少填酌情给分)
14.为了测量水塔的高度,我们取一竹竿,放在阳光下,已知2米长的竹竿投影长为1.5米,在同一时刻测得水塔的投影长为30米,则水塔高为 米.
15.直角坐标系内,身高为1.5米的小强面向y轴站在x轴上的点A(﹣10,0)处,他的前方5米处有一堵墙,已知墙高2米,则站立的小强观察y(y>0)轴时,盲区(视力达不到的地方)范围是 .
16.圆柱的左视图是 ,俯视图是 .
17.如图,小芸用灯泡O照射一个矩形相框ABCD,在墙上形成矩形影子A′B′C′D′.现测得OA=20cm,OA′=50cm,相框ABCD的面积为80cm2,则影子A′B′C′D′的面积为 cm2.
18.如图,是一个四棱锥及它的三视图,其中,图 是它的主视图,图 是它的左视图,图 是它的俯视图.
19.如图所示,是由若干相同大小的小立方体组成的立体图形的三视图,请在右边的立体图形中画出所缺少的小立方体 .
20.一个几何体由几个大小相同的小立方块搭成,从正面和上面看到的这个几何体的形状图如图所示,则该几何体最少是用 个小立方块搭成的.
三.解答题
21.已知如图,AB和DE是直立在地面上的两根立柱,AB=5m,某一时刻AB在阳光下的投影BC=2m.
(1)请你画出此时DE在阳光下的投影;
(2)在测量AB的投影时,同时测量出DE在阳光下的投影长为4m,请你计算DE的长.
22.如图所示,甲物体高4米,影长3米,乙物体高2米,影长4米,两物体相距5米.
(1)在图中画出灯的位置,并画出丙物体的影子.
(2)若灯杆,甲、乙都与地面垂直并且在同一直线上,试求出灯的高度.
23.如图,一墙墩(用线段AB表示)的影子是BC,小明(用线段DE表示)的影子是EF,在M处有一颗大树,它的影子是MN.
(1)试判断是路灯还是太阳光,如果是路灯确定路灯的位置(用点P表示).如果是太阳光请画出光线.
(2)在图中画出表示大树高的线段.
(3)若小明的眼睛近似地看成是点D,试画图分析小明能否看见大树.
24.如图,是由6个大小相同的小立方体块搭建的几何体,其中每个小正方体的棱长为1厘米.
(1)直接写出这个几何体的表面积(包括底部): ;
(2)请按要求在方格内分别画出从这个几何体的三个不同方向看到的形状图.
25.某数学兴趣小组,利用树影测量树高,如图(1),已测出树AB的影长AC为12米,并测出此时太阳光线与地面成30°夹角.
(1)求出树高AB;
(2)因水土流失,此时树AB沿太阳光线方向倒下,在倾倒过程中,树影长度发生了变化,假设太阳光线与地面夹角保持不变.求树的最大影长.(用图(2)解答)
26.如图①是一张长为18cm,宽为12cm的长方形硬纸板.把它的四个角都剪去一个边长为xcm的小正方形,然后把它折成一个无盖的长方体盒子(如图②),请回答下列问题:
(1)折成的无盖长方体盒子的容积V= cm3;(用含x的代数式表示即可,不需化简)
(2)请完成下表,并根据表格回答,当x取什么正整数时,长方体盒子的容积最大?
x/cm 1 2 3 4 5
V/cm3 160 216 80
(3)从正面看折成的长方体盒子,它的形状可能是正方形吗?如果是正方形,求出x的值;如果不是正方形,请说明理由.
参考答案与试题解析
一.选择题
1.解:晚上小亮在路灯下散步,在小亮由A处径直走到B处这一过程中,他在地上的影子先变短,再变长.
故选:B.
2.解:由图片可知,E视点的盲区应该在△ABD的区域内.
故选:C.
3.解:从左边看,得到的图形只有一列两层,第一层是正方形,第二层的正方形里面有实心的圆圈,
故选:B.
4.解:从上面看,是一行两个矩形.
故选:B.
5.解析:光线由上向下照射正五棱柱时的正投影与俯视图一致.
故选:C.
6.解:A、两棵小树的影子的方向相反,不可能为同一时刻阳光下影子,所以A选项错误;
B、两棵小树的影子的方向相反,不可能为同一时刻阳光下影子,所以B选项错误;
C、图中树高与影子成反比,而在同一时刻阳光下,树高与影子成正比,所以C选项错误;
D、在同一时刻阳光下,树高与影子成正比,所以D选项正确.
故选:D.
7.解:三棱锥、圆锥、三棱柱从左面看到的形状都是三角形,而四棱柱从左面看的形状是四边形的,
故选:D.
8.解:如图,根据俯视图标数法,可知最多需要7个,最少需要5个,即x+y=12,
(第2行3个空可相互交换)
故选:A.
9.解:如图所示的一个三棱柱,它的主视图和左视图是.
故选:B.
10.解:三棱柱的主视图为长方形,左视图是三角形,因此选项A符合题意;
圆柱体的主视图、左视图都是长方形,因此选项B不符合题意;
圆锥体的主视图、左视图都是三角形,因此选项C不符合题意;
球体的主视图、左视图包括俯视图都是圆形的,因此选项D不符合题意;
故选:A.
二.填空题
11.解:球的三视图都是圆.
故答案为:圆.
12.解:当直角三角形和平面垂直的时候,其投影为一条线段,当直角三角形与平面的夹角不为90°时,其投影为三角形.
13.解:综合主视图与左视图,有3行3列.故图形可能是①②③.
故答案为:①②③.
14.解:∵=,
∴水塔的高度=×水塔的影长=×30=40(m).
故答案为:40米.
15.解:过D作DF⊥OC于F,交BE于H,OF=1.5,BH=0.5,
三角形DBH中,tan∠BDH=BH:DH=0.5:5,
因此三角形CDF中,CF=DF tan∠BDH=1
因此,OC=OF+CF=1+1.5=2.5.因此盲区的范围在0<y≤2.5.
16.解:圆柱的左视图是矩形,俯视图是圆.
17.解:∵OA:OA′=2:5,
可知OB:OB′=2:5,
∵∠AOB=∠A′OB′,
∴△AOB∽△A′OB′,
∴AB:A′B′=2:5,
∴矩形ABCD的面积:矩形A′B′C′D′的面积为4:25,
又矩形ABCD的面积为80cm2,则矩形A′B′C′D′的面积为500cm2.
故答案为:500cm2.
18.解:从上面看四棱锥是一长方形加两条对角线,那么B是俯视图;由俯视图易得从正面看四棱锥是一个底边较大的三角形,故选C;从左面看四棱锥是一个底边较小的三角形,故选A.
19.解:
20.解:从俯视图上看各个位置至少放1个小立方体,从主视图上看第一列至少有一个位置放3个小立方体,第三列至少有一个位置放2个小立方体,
因此至少需要10个,
故答案为:10.
三.解答题
21.解:(1)如图,EF为此时DE在阳光下的投影;
(2)∵AC∥DF,
∴∠ACB=∠DFE,
∴Rt△ABC∽Rt△DEF,
∴=,即=,解得DE=10(m),
即DE的长为10m.
22.解:(1)点O为灯的位置,QF为丙物体的影子;
(2)作OM⊥QH 设OM=x,BM=y,
由△GAB∽△GOM得=
即:①,
由△CDH∽△OMH得
即:②
由①②得,
x=4.8,y=0.6.
答灯的高度为4.8米.
23.解:(1)根据光线相交于一点,即可得出路灯确定路灯的位置;
(2)如图所示:
(3)如图所示,小明的眼睛近似地看成是点D,小明不能看见大树.
24.解:(1)(5+4+4)×2=26(cm2),
故答案为:26cm2;
(2)根据三视图的画法,画出相应的图形如下:
25.解:(1)AB=ACtan30°=12×=4(米).
答:树高约为4米.
(2)如图(2),B1N=AN=AB1sin45°=4×=2(米).
NC1=NB1tan60°=2×=6(米).
AC1=AN+NC1=2+6.
当树与地面成60°角时影长最大AC2(或树与光线垂直时影长最大或光线与半径为AB的⊙A相切时影长最大)
AC2=2AB2=;
26.解:(1)由题意得,长方体盒子的长(18﹣2x)、宽(12﹣2x)、高x,因此体积为:(18﹣2x) (12﹣2x) x,
故答案为:(18﹣2x) (12﹣2x) x,
(2)把x=2代入(18﹣2x) (12﹣2x) x得,(18﹣2x) (12﹣2x) x=14×8×2=224,
把x=4代入(18﹣2x) (12﹣2x) x得,(18﹣2x) (12﹣2x) x=10×4×4=160,
故答案为:224,160;
(3)它的形状不可能是正方形,
当18﹣2x=x时,即x=6,而当x=6时,图①的长边变为0,因此折不成长方体,故从正面看是正方形是不可能的.
一.选择题
1.如图,晚上小亮在路灯下散步,在小亮由A处径直走到B处这一过程中,他在地上的影子( )
A.逐渐变短 B.先变短后变长
C.先变长后变短 D.逐渐变长
2.如图,在房子屋檐E处安有一台监视器,房子前有一面落地的广告牌,那么监视器的盲区是( )
A.△ACE B.△ADF C.△ABD D.四边形BCED
3.如图,这是一个机械模具,则它的左视图是( )
A. B. C. D.
4.如图所示,该几何体的俯视图是( )
A. B. C. D.
5.如图,光线由上向下照射正五棱柱时的正投影是( )
A. B.
C. D.
6.在下列四幅图形中,能表示两棵小树在同一时刻阳光下影子的图形的可能是( )
A.
B.
C.
D.
7.下面立体图形中,从左面看到的平面图形与其他三个不一样的是( )
A. B.
C. D.
8.用小立方块搭成的几何体,从左面看和从上面看如下,这样的几何体最多要x个小立方块,最少要y个小立方块,则x+y等于( )
A.12 B.13 C.14 D.15
9.如图所示是一个三棱柱,画出它的主视图和左视图均正确的是( )
A. B.
C. D.
10.下列几何体的主视图与左视图不相同的是( )
A. B.
C. D.
二.填空题
11.球的主视图、俯视图、左视图都是 .
12.直角三角形的正投影可能是 .
13.如右图,是一个由若干个小正方体搭建而成的几何体的主视图与左视图,那么下列图形中可以作为该几何体的俯视图的序号是 (多填或错填得0分,少填酌情给分)
14.为了测量水塔的高度,我们取一竹竿,放在阳光下,已知2米长的竹竿投影长为1.5米,在同一时刻测得水塔的投影长为30米,则水塔高为 米.
15.直角坐标系内,身高为1.5米的小强面向y轴站在x轴上的点A(﹣10,0)处,他的前方5米处有一堵墙,已知墙高2米,则站立的小强观察y(y>0)轴时,盲区(视力达不到的地方)范围是 .
16.圆柱的左视图是 ,俯视图是 .
17.如图,小芸用灯泡O照射一个矩形相框ABCD,在墙上形成矩形影子A′B′C′D′.现测得OA=20cm,OA′=50cm,相框ABCD的面积为80cm2,则影子A′B′C′D′的面积为 cm2.
18.如图,是一个四棱锥及它的三视图,其中,图 是它的主视图,图 是它的左视图,图 是它的俯视图.
19.如图所示,是由若干相同大小的小立方体组成的立体图形的三视图,请在右边的立体图形中画出所缺少的小立方体 .
20.一个几何体由几个大小相同的小立方块搭成,从正面和上面看到的这个几何体的形状图如图所示,则该几何体最少是用 个小立方块搭成的.
三.解答题
21.已知如图,AB和DE是直立在地面上的两根立柱,AB=5m,某一时刻AB在阳光下的投影BC=2m.
(1)请你画出此时DE在阳光下的投影;
(2)在测量AB的投影时,同时测量出DE在阳光下的投影长为4m,请你计算DE的长.
22.如图所示,甲物体高4米,影长3米,乙物体高2米,影长4米,两物体相距5米.
(1)在图中画出灯的位置,并画出丙物体的影子.
(2)若灯杆,甲、乙都与地面垂直并且在同一直线上,试求出灯的高度.
23.如图,一墙墩(用线段AB表示)的影子是BC,小明(用线段DE表示)的影子是EF,在M处有一颗大树,它的影子是MN.
(1)试判断是路灯还是太阳光,如果是路灯确定路灯的位置(用点P表示).如果是太阳光请画出光线.
(2)在图中画出表示大树高的线段.
(3)若小明的眼睛近似地看成是点D,试画图分析小明能否看见大树.
24.如图,是由6个大小相同的小立方体块搭建的几何体,其中每个小正方体的棱长为1厘米.
(1)直接写出这个几何体的表面积(包括底部): ;
(2)请按要求在方格内分别画出从这个几何体的三个不同方向看到的形状图.
25.某数学兴趣小组,利用树影测量树高,如图(1),已测出树AB的影长AC为12米,并测出此时太阳光线与地面成30°夹角.
(1)求出树高AB;
(2)因水土流失,此时树AB沿太阳光线方向倒下,在倾倒过程中,树影长度发生了变化,假设太阳光线与地面夹角保持不变.求树的最大影长.(用图(2)解答)
26.如图①是一张长为18cm,宽为12cm的长方形硬纸板.把它的四个角都剪去一个边长为xcm的小正方形,然后把它折成一个无盖的长方体盒子(如图②),请回答下列问题:
(1)折成的无盖长方体盒子的容积V= cm3;(用含x的代数式表示即可,不需化简)
(2)请完成下表,并根据表格回答,当x取什么正整数时,长方体盒子的容积最大?
x/cm 1 2 3 4 5
V/cm3 160 216 80
(3)从正面看折成的长方体盒子,它的形状可能是正方形吗?如果是正方形,求出x的值;如果不是正方形,请说明理由.
参考答案与试题解析
一.选择题
1.解:晚上小亮在路灯下散步,在小亮由A处径直走到B处这一过程中,他在地上的影子先变短,再变长.
故选:B.
2.解:由图片可知,E视点的盲区应该在△ABD的区域内.
故选:C.
3.解:从左边看,得到的图形只有一列两层,第一层是正方形,第二层的正方形里面有实心的圆圈,
故选:B.
4.解:从上面看,是一行两个矩形.
故选:B.
5.解析:光线由上向下照射正五棱柱时的正投影与俯视图一致.
故选:C.
6.解:A、两棵小树的影子的方向相反,不可能为同一时刻阳光下影子,所以A选项错误;
B、两棵小树的影子的方向相反,不可能为同一时刻阳光下影子,所以B选项错误;
C、图中树高与影子成反比,而在同一时刻阳光下,树高与影子成正比,所以C选项错误;
D、在同一时刻阳光下,树高与影子成正比,所以D选项正确.
故选:D.
7.解:三棱锥、圆锥、三棱柱从左面看到的形状都是三角形,而四棱柱从左面看的形状是四边形的,
故选:D.
8.解:如图,根据俯视图标数法,可知最多需要7个,最少需要5个,即x+y=12,
(第2行3个空可相互交换)
故选:A.
9.解:如图所示的一个三棱柱,它的主视图和左视图是.
故选:B.
10.解:三棱柱的主视图为长方形,左视图是三角形,因此选项A符合题意;
圆柱体的主视图、左视图都是长方形,因此选项B不符合题意;
圆锥体的主视图、左视图都是三角形,因此选项C不符合题意;
球体的主视图、左视图包括俯视图都是圆形的,因此选项D不符合题意;
故选:A.
二.填空题
11.解:球的三视图都是圆.
故答案为:圆.
12.解:当直角三角形和平面垂直的时候,其投影为一条线段,当直角三角形与平面的夹角不为90°时,其投影为三角形.
13.解:综合主视图与左视图,有3行3列.故图形可能是①②③.
故答案为:①②③.
14.解:∵=,
∴水塔的高度=×水塔的影长=×30=40(m).
故答案为:40米.
15.解:过D作DF⊥OC于F,交BE于H,OF=1.5,BH=0.5,
三角形DBH中,tan∠BDH=BH:DH=0.5:5,
因此三角形CDF中,CF=DF tan∠BDH=1
因此,OC=OF+CF=1+1.5=2.5.因此盲区的范围在0<y≤2.5.
16.解:圆柱的左视图是矩形,俯视图是圆.
17.解:∵OA:OA′=2:5,
可知OB:OB′=2:5,
∵∠AOB=∠A′OB′,
∴△AOB∽△A′OB′,
∴AB:A′B′=2:5,
∴矩形ABCD的面积:矩形A′B′C′D′的面积为4:25,
又矩形ABCD的面积为80cm2,则矩形A′B′C′D′的面积为500cm2.
故答案为:500cm2.
18.解:从上面看四棱锥是一长方形加两条对角线,那么B是俯视图;由俯视图易得从正面看四棱锥是一个底边较大的三角形,故选C;从左面看四棱锥是一个底边较小的三角形,故选A.
19.解:
20.解:从俯视图上看各个位置至少放1个小立方体,从主视图上看第一列至少有一个位置放3个小立方体,第三列至少有一个位置放2个小立方体,
因此至少需要10个,
故答案为:10.
三.解答题
21.解:(1)如图,EF为此时DE在阳光下的投影;
(2)∵AC∥DF,
∴∠ACB=∠DFE,
∴Rt△ABC∽Rt△DEF,
∴=,即=,解得DE=10(m),
即DE的长为10m.
22.解:(1)点O为灯的位置,QF为丙物体的影子;
(2)作OM⊥QH 设OM=x,BM=y,
由△GAB∽△GOM得=
即:①,
由△CDH∽△OMH得
即:②
由①②得,
x=4.8,y=0.6.
答灯的高度为4.8米.
23.解:(1)根据光线相交于一点,即可得出路灯确定路灯的位置;
(2)如图所示:
(3)如图所示,小明的眼睛近似地看成是点D,小明不能看见大树.
24.解:(1)(5+4+4)×2=26(cm2),
故答案为:26cm2;
(2)根据三视图的画法,画出相应的图形如下:
25.解:(1)AB=ACtan30°=12×=4(米).
答:树高约为4米.
(2)如图(2),B1N=AN=AB1sin45°=4×=2(米).
NC1=NB1tan60°=2×=6(米).
AC1=AN+NC1=2+6.
当树与地面成60°角时影长最大AC2(或树与光线垂直时影长最大或光线与半径为AB的⊙A相切时影长最大)
AC2=2AB2=;
26.解:(1)由题意得,长方体盒子的长(18﹣2x)、宽(12﹣2x)、高x,因此体积为:(18﹣2x) (12﹣2x) x,
故答案为:(18﹣2x) (12﹣2x) x,
(2)把x=2代入(18﹣2x) (12﹣2x) x得,(18﹣2x) (12﹣2x) x=14×8×2=224,
把x=4代入(18﹣2x) (12﹣2x) x得,(18﹣2x) (12﹣2x) x=10×4×4=160,
故答案为:224,160;
(3)它的形状不可能是正方形,
当18﹣2x=x时,即x=6,而当x=6时,图①的长边变为0,因此折不成长方体,故从正面看是正方形是不可能的.
