2021-2022学年鲁教五四新版七年级上册数学《第5章 位置与坐标》单元测试卷(word版含解析)
文档属性
| 名称 | 2021-2022学年鲁教五四新版七年级上册数学《第5章 位置与坐标》单元测试卷(word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 219.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-26 16:55:47 | ||
图片预览



文档简介
2021-2022学年鲁教五四新版七年级上册数学《第5章 位置与坐标》单元测试卷
一.选择题
1.已知点P(x,y),且xy>0,点P到x轴的距离是3个单位,到y轴的距离是2个单位,则点P的坐标是( )
A.(2,3) B.(3,2)
C.(2,3)或(﹣2,﹣3) D.(﹣3,﹣2)
2.如图,已知棋子“卒”的坐标为 (﹣2,3),棋子“马”的坐标为(1,3),则棋子“炮”的坐标为( )
A.(2,2) B.(4,1) C.(﹣2,2) D.(4,2)
3.在平面直角坐标系中,点A(5,﹣4)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.如果点P(5,y)在第四象限,则y的取值范围是( )
A.y<0 B.y>0 C.y≤0 D.y≥0
5.点P(2,﹣3)关于y轴对称点的坐标是( )
A.(2,3) B.(﹣2,﹣3) C.(2,﹣3) D.(﹣2,3)
6.在平面直角坐标系中,点P(﹣3,2)关于x轴对称的点的坐标是( )
A.(3,2) B.(2,﹣3) C.(﹣3,2) D.(﹣3,﹣2)
7.如图,这是一所学校的平面示意图,在同一平面直角坐标系中,教学楼A的坐标为(﹣3,0),实验楼B的坐标为(2,0),则图书馆C的坐标为( )
A.(0,﹣3) B.(﹣1,﹣3) C.(3,0) D.(﹣2,0)
8.若点M(3,﹣2)与点N(x、y)在同一条平行于x轴的直线上,且MN=1,则N点的坐标为( )
A.(4,﹣2) B.(3,﹣1)
C.(3,﹣1)或(3,﹣3) D.(4,﹣2)或(2,﹣2)
9.如图,在平面直角坐标系中,AB平行于x轴,点A坐标为(5,3),B在A点的左侧,AB=a,若B点在第二象限,则a的取值范围是( )
A.a>5 B.a≥5 C.a>3 D.a≥3
10.若点A(a,5),在第二象限,则点A关于直线m(直线m上各点的横坐标都是1)对称的点坐标是( )
A.(﹣a,5) B.(2﹣a,5) C.(﹣a﹣4,﹣5) D.(﹣a﹣2,﹣5)
二.填空题
11.已知点A(m﹣1,2m)在y轴上,则点A的坐标为 .
12.在第二象限内的点P到x轴的距离是3,到y轴的距离是4,则点P的坐标是 .
13.如图,象棋盘上,若“将”位于点(1,﹣1),“车”位于点(﹣3,﹣1),则“马”位于点 .
14.如图,已知棋子“车”的坐标为(﹣2,﹣1),棋子“马”的坐标为(1,﹣1),则棋子“炮”的坐标为 .
15.点P(5,﹣12)到原点的距离是 .
16.点A(﹣1,2)关于y轴的对称点坐标是 .
17.已知点A(2,m+3)与B(n,﹣4)关于x轴对称,则m+n= .
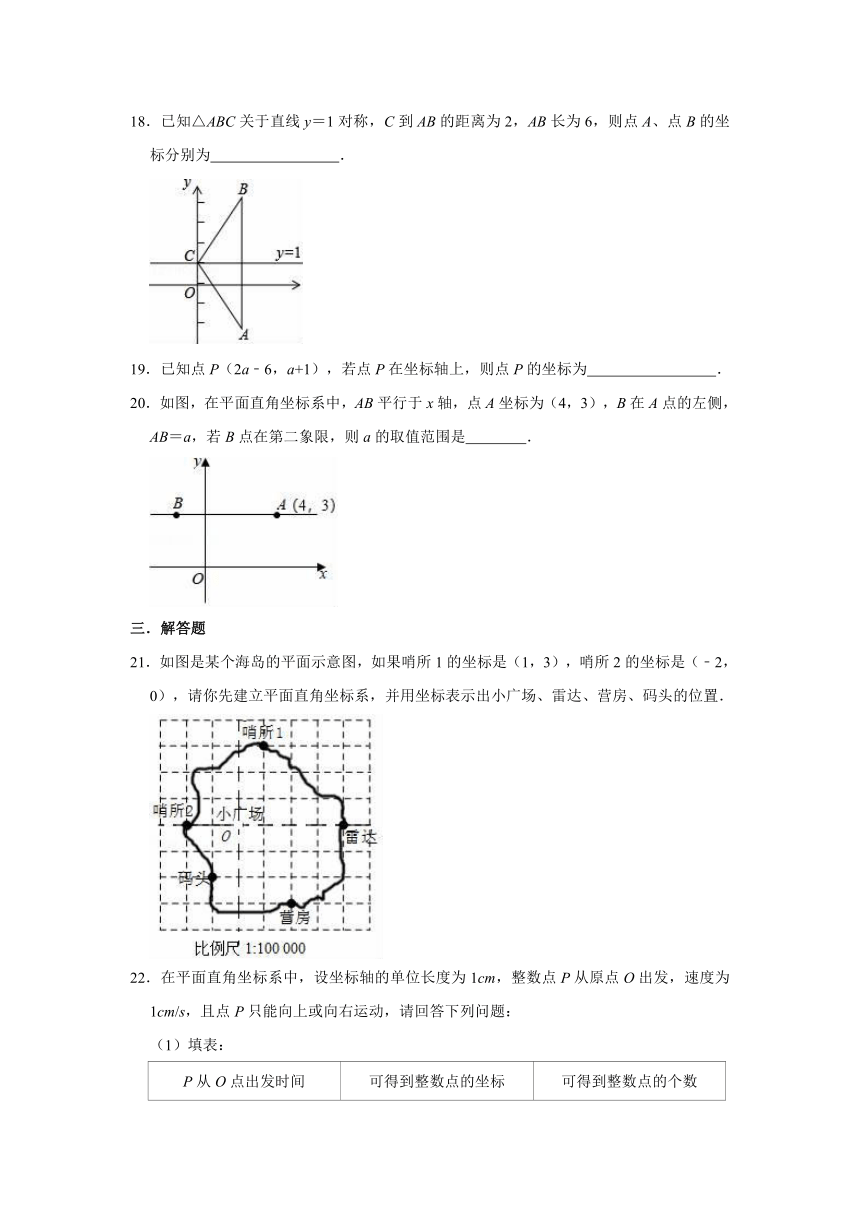
18.已知△ABC关于直线y=1对称,C到AB的距离为2,AB长为6,则点A、点B的坐标分别为 .
19.已知点P(2a﹣6,a+1),若点P在坐标轴上,则点P的坐标为 .
20.如图,在平面直角坐标系中,AB平行于x轴,点A坐标为(4,3),B在A点的左侧,AB=a,若B点在第二象限,则a的取值范围是 .
三.解答题
21.如图是某个海岛的平面示意图,如果哨所1的坐标是(1,3),哨所2的坐标是(﹣2,0),请你先建立平面直角坐标系,并用坐标表示出小广场、雷达、营房、码头的位置.
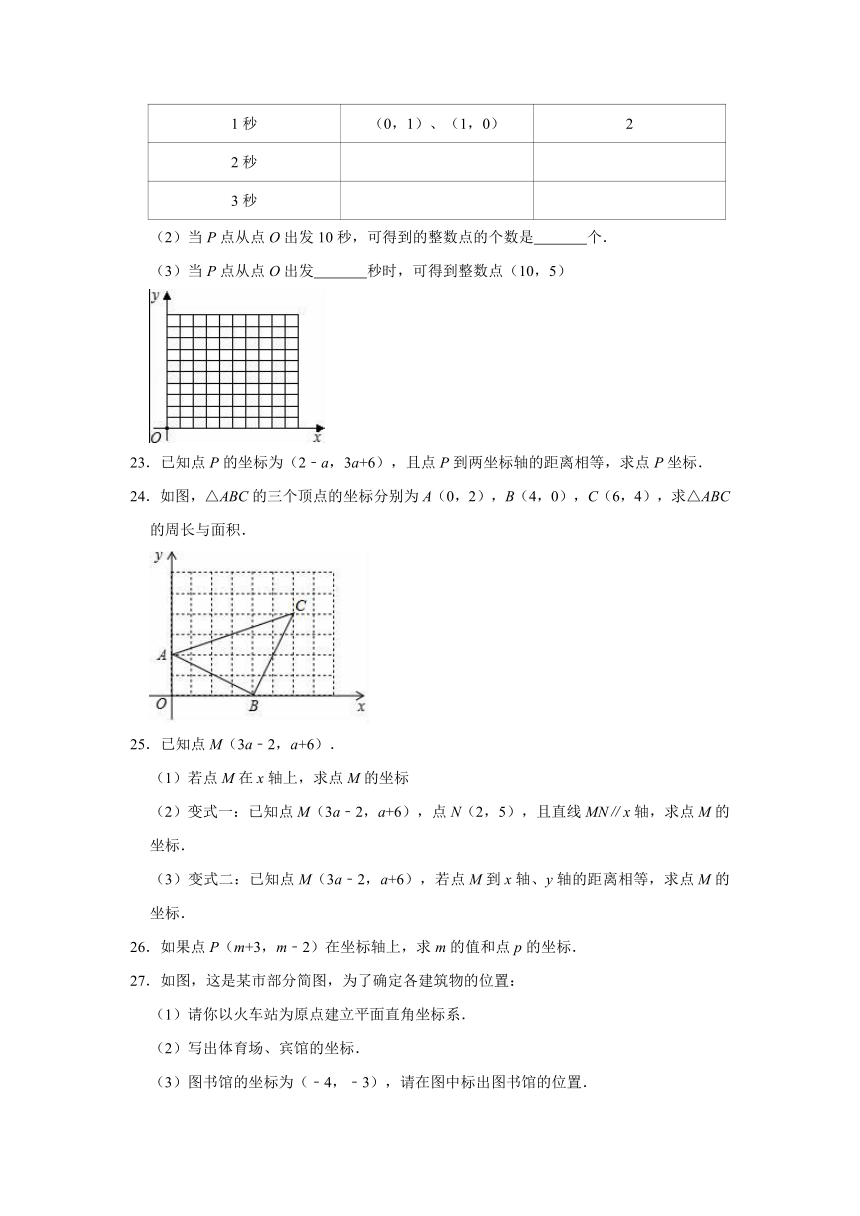
22.在平面直角坐标系中,设坐标轴的单位长度为1cm,整数点P从原点O出发,速度为1cm/s,且点P只能向上或向右运动,请回答下列问题:
(1)填表:
P从O点出发时间 可得到整数点的坐标 可得到整数点的个数
1秒 (0,1)、(1,0) 2
2秒
3秒
(2)当P点从点O出发10秒,可得到的整数点的个数是 个.
(3)当P点从点O出发 秒时,可得到整数点(10,5)
23.已知点P的坐标为(2﹣a,3a+6),且点P到两坐标轴的距离相等,求点P坐标.
24.如图,△ABC的三个顶点的坐标分别为A(0,2),B(4,0),C(6,4),求△ABC的周长与面积.
25.已知点M(3a﹣2,a+6).
(1)若点M在x轴上,求点M的坐标
(2)变式一:已知点M(3a﹣2,a+6),点N(2,5),且直线MN∥x轴,求点M的坐标.
(3)变式二:已知点M(3a﹣2,a+6),若点M到x轴、y轴的距离相等,求点M的坐标.
26.如果点P(m+3,m﹣2)在坐标轴上,求m的值和点p的坐标.
27.如图,这是某市部分简图,为了确定各建筑物的位置:
(1)请你以火车站为原点建立平面直角坐标系.
(2)写出体育场、宾馆的坐标.
(3)图书馆的坐标为(﹣4,﹣3),请在图中标出图书馆的位置.
参考答案与试题解析
一.选择题
1.解:∵xy>0,
∴x、y同号,
∵点P到x轴的距离是3个单位,到y轴的距离是2个单位,
∴点P的横坐标是2或﹣2,纵坐标是3或﹣3,
∴点P的坐标是(2,3)或(﹣2,﹣3).
故选:C.
2.解:如图:
棋子“炮”的坐标为(4,2).
故选:D.
3.解:A(5,﹣4)在第四象限,
故选:D.
4.解:∵点P(5,y)在第四象限,
∴y<0.
故选:A.
5.解:点P(2,﹣3)关于y轴对称点的坐标是(﹣2,﹣3).
故选:B.
6.解:根据轴对称的性质,得点P(﹣3,2)关于x轴对称的点的坐标为(﹣3,﹣2).
故选:D.
7.解:如图所示:图书馆C的坐标为(﹣1,﹣3).
故选:B.
8.解:∵点M(3,﹣2)与点N(x、y)在同一条平行于x轴的直线上,MN=1,
∴y=﹣2,|x﹣3|=1,
∴x=2或4,
∴N点的坐标为(2,﹣2)或(4,﹣2).
故选:D.
9.解:设点B横坐标为x,
∵AB平行于x轴,点A坐标为(5,3),B在A点的左侧,AB=a,
∴a=5﹣x,
∴x=5﹣a,
∵B点在第二象限,
∴5﹣a<0,
∴a>5.
故选:A.
10.解:∵直线m上各点的横坐标都是1,
∴直线为:x=1,
∵点P(a,5)在第二象限,
∴a到1的距离为:1﹣a,
∴点P关于直线m对称的点的横坐标是:1﹣a+1=2﹣a,
故P点对称的点的坐标是:(2﹣a,5).
故选:B.
二.填空题
11.解:∵点A(m﹣1,2m)在y轴上,
∴点A的横坐标是0,
∴m﹣1=0,解得m=1,
∴2m=2,点A的纵坐标为2,
∴点A的坐标是(0,2).
故答案为:(0,2).
12.解:第二象限内的点横坐标小于0,纵坐标大于0;到x轴的距离是3,说明点的纵坐标为3,到y轴的距离为4,说明点的横坐标为﹣4,因而点P的坐标是(﹣4,3).故答案填:(﹣4,3).
13.解:建立平面直角坐标系如图,
“马”位于(4,2).
故答案为:(4,2).
14.解:如图,棋子“炮”的坐标为(3,﹣2).
故答案为:(3,﹣2).
15.解:如图,设原点为O,作PA⊥x轴于点A,那么PA=12,OA=5,根据勾股定理可得OP==13.故答案填13.
16.解:由平面直角坐标系中关于y轴对称的点的坐标特点:横坐标相反数,纵坐标不变,
可得:点A关于y轴的对称点的坐标是(1,2).
17.解:由点A(2,m+3)与B(n,﹣4)关于x轴对称,得:n=2,m+3=4,
所以m=1,n=2,
则m+n=2+1=3.
故答案为:3.
18.解:由题可知:可得A、B的连线与y=1垂直,且两点到直线y=1的距离相等
∵AB=6
∴A、B两点的纵坐标分别为﹣2和4
又∵C到AB的距离为2
∴A、B两点的横坐标都为2
∴A、B两点的坐标分别为(2,﹣2)(2,4).
19.解:当P在x轴上时,a+1=0,解得a=﹣1,P(﹣8,0);
当P在y轴上时,2a﹣6=0,解得a=3,P(0,4).
所以P(﹣8,0)或(0,4).
故答案为(﹣8,0)或(0,4).
20.解:由题意﹣(a﹣4)<0,
解得a>4,
故答案为:a>4.
三.解答题
21.解:建立如图所示的平面直角坐标系:
小广场(0,0)、雷达(4,0)、营房(2,﹣3)、码头(﹣1,﹣2).
22.解:(1)以1秒时达到的整数点为基准,向上或向右移动一格得到2秒时的可能的整数点;再以2秒时得到的整数点为基准,向上或向右移动一格,得到3秒时可能得到的整数点.
P从O点出发时间 可得到整数点的坐标 可得到整数点的个数
1秒 (0,1)、(1,0) 2
2秒 (0,2),(2,0),(1,1) 3
3秒 (0,3),(3,0),(2,1),(1,2) 4
(2)1秒时,达到2个整数点;2秒时,达到3个整数点;3秒时,达到4个整数点,那么10秒时,应达到11个整数点;
(3)横坐标为10,需要从原点开始沿x轴向右移动10秒,纵坐标为5,需再向上移动5秒,所以需要的时间为15秒.
23.解:∵点P的坐标为(2﹣a,3a+6),且点P到两坐标轴的距离相等,
∴2﹣a=3a+6或(2﹣a)+(3a+6)=0;
解得:a=﹣1或a=﹣4,
∴P点坐标为(3,3)或(6,﹣6).
24.解:∵A(0,2),B(4,0),C(6,4),
∴AB==2,BC==2,AC==2,
∴△ABC的周长=AB+BC+AC=2+2+2=4+2;
∵AB2+BC2=AC2,
∴△ABC为直角三角形,∠ABC=90°,
∴△ABC的面积= 2 2=10.
25.解:(1)∵点M在x轴上,
∴a+6=0,
∴a=﹣6,
3a﹣2=﹣18﹣2=﹣20,a+6=0,
∴点M的坐标是(﹣20,0);
(2)∵直线MN∥x轴,
∴a+6=5,
解得a=﹣1,
3a﹣2=3×(﹣1)﹣2=﹣5,
所以,点M的坐标为(﹣5,5).
(3)∵点M到x轴、y轴的距离相等,
∴3a﹣2=a+6,或3a﹣2+a+6=0
解得:a=4,或a=﹣1,
所以点M的坐标为(10,10)或(﹣5,5).
26.解:∵点P(m+3,m﹣2)在坐标轴上,
∴m+3=0或m﹣2=0,
∴m=﹣3或m=2,
∴点P(0,﹣5)或(5,0).
27.解:(1)以火车站为坐标原点建立的平面直角坐标系如图所示:
(2)体育场(﹣4,3)、宾馆(2,2);
(3)图书馆位置如图所示.
一.选择题
1.已知点P(x,y),且xy>0,点P到x轴的距离是3个单位,到y轴的距离是2个单位,则点P的坐标是( )
A.(2,3) B.(3,2)
C.(2,3)或(﹣2,﹣3) D.(﹣3,﹣2)
2.如图,已知棋子“卒”的坐标为 (﹣2,3),棋子“马”的坐标为(1,3),则棋子“炮”的坐标为( )
A.(2,2) B.(4,1) C.(﹣2,2) D.(4,2)
3.在平面直角坐标系中,点A(5,﹣4)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.如果点P(5,y)在第四象限,则y的取值范围是( )
A.y<0 B.y>0 C.y≤0 D.y≥0
5.点P(2,﹣3)关于y轴对称点的坐标是( )
A.(2,3) B.(﹣2,﹣3) C.(2,﹣3) D.(﹣2,3)
6.在平面直角坐标系中,点P(﹣3,2)关于x轴对称的点的坐标是( )
A.(3,2) B.(2,﹣3) C.(﹣3,2) D.(﹣3,﹣2)
7.如图,这是一所学校的平面示意图,在同一平面直角坐标系中,教学楼A的坐标为(﹣3,0),实验楼B的坐标为(2,0),则图书馆C的坐标为( )
A.(0,﹣3) B.(﹣1,﹣3) C.(3,0) D.(﹣2,0)
8.若点M(3,﹣2)与点N(x、y)在同一条平行于x轴的直线上,且MN=1,则N点的坐标为( )
A.(4,﹣2) B.(3,﹣1)
C.(3,﹣1)或(3,﹣3) D.(4,﹣2)或(2,﹣2)
9.如图,在平面直角坐标系中,AB平行于x轴,点A坐标为(5,3),B在A点的左侧,AB=a,若B点在第二象限,则a的取值范围是( )
A.a>5 B.a≥5 C.a>3 D.a≥3
10.若点A(a,5),在第二象限,则点A关于直线m(直线m上各点的横坐标都是1)对称的点坐标是( )
A.(﹣a,5) B.(2﹣a,5) C.(﹣a﹣4,﹣5) D.(﹣a﹣2,﹣5)
二.填空题
11.已知点A(m﹣1,2m)在y轴上,则点A的坐标为 .
12.在第二象限内的点P到x轴的距离是3,到y轴的距离是4,则点P的坐标是 .
13.如图,象棋盘上,若“将”位于点(1,﹣1),“车”位于点(﹣3,﹣1),则“马”位于点 .
14.如图,已知棋子“车”的坐标为(﹣2,﹣1),棋子“马”的坐标为(1,﹣1),则棋子“炮”的坐标为 .
15.点P(5,﹣12)到原点的距离是 .
16.点A(﹣1,2)关于y轴的对称点坐标是 .
17.已知点A(2,m+3)与B(n,﹣4)关于x轴对称,则m+n= .
18.已知△ABC关于直线y=1对称,C到AB的距离为2,AB长为6,则点A、点B的坐标分别为 .
19.已知点P(2a﹣6,a+1),若点P在坐标轴上,则点P的坐标为 .
20.如图,在平面直角坐标系中,AB平行于x轴,点A坐标为(4,3),B在A点的左侧,AB=a,若B点在第二象限,则a的取值范围是 .
三.解答题
21.如图是某个海岛的平面示意图,如果哨所1的坐标是(1,3),哨所2的坐标是(﹣2,0),请你先建立平面直角坐标系,并用坐标表示出小广场、雷达、营房、码头的位置.
22.在平面直角坐标系中,设坐标轴的单位长度为1cm,整数点P从原点O出发,速度为1cm/s,且点P只能向上或向右运动,请回答下列问题:
(1)填表:
P从O点出发时间 可得到整数点的坐标 可得到整数点的个数
1秒 (0,1)、(1,0) 2
2秒
3秒
(2)当P点从点O出发10秒,可得到的整数点的个数是 个.
(3)当P点从点O出发 秒时,可得到整数点(10,5)
23.已知点P的坐标为(2﹣a,3a+6),且点P到两坐标轴的距离相等,求点P坐标.
24.如图,△ABC的三个顶点的坐标分别为A(0,2),B(4,0),C(6,4),求△ABC的周长与面积.
25.已知点M(3a﹣2,a+6).
(1)若点M在x轴上,求点M的坐标
(2)变式一:已知点M(3a﹣2,a+6),点N(2,5),且直线MN∥x轴,求点M的坐标.
(3)变式二:已知点M(3a﹣2,a+6),若点M到x轴、y轴的距离相等,求点M的坐标.
26.如果点P(m+3,m﹣2)在坐标轴上,求m的值和点p的坐标.
27.如图,这是某市部分简图,为了确定各建筑物的位置:
(1)请你以火车站为原点建立平面直角坐标系.
(2)写出体育场、宾馆的坐标.
(3)图书馆的坐标为(﹣4,﹣3),请在图中标出图书馆的位置.
参考答案与试题解析
一.选择题
1.解:∵xy>0,
∴x、y同号,
∵点P到x轴的距离是3个单位,到y轴的距离是2个单位,
∴点P的横坐标是2或﹣2,纵坐标是3或﹣3,
∴点P的坐标是(2,3)或(﹣2,﹣3).
故选:C.
2.解:如图:
棋子“炮”的坐标为(4,2).
故选:D.
3.解:A(5,﹣4)在第四象限,
故选:D.
4.解:∵点P(5,y)在第四象限,
∴y<0.
故选:A.
5.解:点P(2,﹣3)关于y轴对称点的坐标是(﹣2,﹣3).
故选:B.
6.解:根据轴对称的性质,得点P(﹣3,2)关于x轴对称的点的坐标为(﹣3,﹣2).
故选:D.
7.解:如图所示:图书馆C的坐标为(﹣1,﹣3).
故选:B.
8.解:∵点M(3,﹣2)与点N(x、y)在同一条平行于x轴的直线上,MN=1,
∴y=﹣2,|x﹣3|=1,
∴x=2或4,
∴N点的坐标为(2,﹣2)或(4,﹣2).
故选:D.
9.解:设点B横坐标为x,
∵AB平行于x轴,点A坐标为(5,3),B在A点的左侧,AB=a,
∴a=5﹣x,
∴x=5﹣a,
∵B点在第二象限,
∴5﹣a<0,
∴a>5.
故选:A.
10.解:∵直线m上各点的横坐标都是1,
∴直线为:x=1,
∵点P(a,5)在第二象限,
∴a到1的距离为:1﹣a,
∴点P关于直线m对称的点的横坐标是:1﹣a+1=2﹣a,
故P点对称的点的坐标是:(2﹣a,5).
故选:B.
二.填空题
11.解:∵点A(m﹣1,2m)在y轴上,
∴点A的横坐标是0,
∴m﹣1=0,解得m=1,
∴2m=2,点A的纵坐标为2,
∴点A的坐标是(0,2).
故答案为:(0,2).
12.解:第二象限内的点横坐标小于0,纵坐标大于0;到x轴的距离是3,说明点的纵坐标为3,到y轴的距离为4,说明点的横坐标为﹣4,因而点P的坐标是(﹣4,3).故答案填:(﹣4,3).
13.解:建立平面直角坐标系如图,
“马”位于(4,2).
故答案为:(4,2).
14.解:如图,棋子“炮”的坐标为(3,﹣2).
故答案为:(3,﹣2).
15.解:如图,设原点为O,作PA⊥x轴于点A,那么PA=12,OA=5,根据勾股定理可得OP==13.故答案填13.
16.解:由平面直角坐标系中关于y轴对称的点的坐标特点:横坐标相反数,纵坐标不变,
可得:点A关于y轴的对称点的坐标是(1,2).
17.解:由点A(2,m+3)与B(n,﹣4)关于x轴对称,得:n=2,m+3=4,
所以m=1,n=2,
则m+n=2+1=3.
故答案为:3.
18.解:由题可知:可得A、B的连线与y=1垂直,且两点到直线y=1的距离相等
∵AB=6
∴A、B两点的纵坐标分别为﹣2和4
又∵C到AB的距离为2
∴A、B两点的横坐标都为2
∴A、B两点的坐标分别为(2,﹣2)(2,4).
19.解:当P在x轴上时,a+1=0,解得a=﹣1,P(﹣8,0);
当P在y轴上时,2a﹣6=0,解得a=3,P(0,4).
所以P(﹣8,0)或(0,4).
故答案为(﹣8,0)或(0,4).
20.解:由题意﹣(a﹣4)<0,
解得a>4,
故答案为:a>4.
三.解答题
21.解:建立如图所示的平面直角坐标系:
小广场(0,0)、雷达(4,0)、营房(2,﹣3)、码头(﹣1,﹣2).
22.解:(1)以1秒时达到的整数点为基准,向上或向右移动一格得到2秒时的可能的整数点;再以2秒时得到的整数点为基准,向上或向右移动一格,得到3秒时可能得到的整数点.
P从O点出发时间 可得到整数点的坐标 可得到整数点的个数
1秒 (0,1)、(1,0) 2
2秒 (0,2),(2,0),(1,1) 3
3秒 (0,3),(3,0),(2,1),(1,2) 4
(2)1秒时,达到2个整数点;2秒时,达到3个整数点;3秒时,达到4个整数点,那么10秒时,应达到11个整数点;
(3)横坐标为10,需要从原点开始沿x轴向右移动10秒,纵坐标为5,需再向上移动5秒,所以需要的时间为15秒.
23.解:∵点P的坐标为(2﹣a,3a+6),且点P到两坐标轴的距离相等,
∴2﹣a=3a+6或(2﹣a)+(3a+6)=0;
解得:a=﹣1或a=﹣4,
∴P点坐标为(3,3)或(6,﹣6).
24.解:∵A(0,2),B(4,0),C(6,4),
∴AB==2,BC==2,AC==2,
∴△ABC的周长=AB+BC+AC=2+2+2=4+2;
∵AB2+BC2=AC2,
∴△ABC为直角三角形,∠ABC=90°,
∴△ABC的面积= 2 2=10.
25.解:(1)∵点M在x轴上,
∴a+6=0,
∴a=﹣6,
3a﹣2=﹣18﹣2=﹣20,a+6=0,
∴点M的坐标是(﹣20,0);
(2)∵直线MN∥x轴,
∴a+6=5,
解得a=﹣1,
3a﹣2=3×(﹣1)﹣2=﹣5,
所以,点M的坐标为(﹣5,5).
(3)∵点M到x轴、y轴的距离相等,
∴3a﹣2=a+6,或3a﹣2+a+6=0
解得:a=4,或a=﹣1,
所以点M的坐标为(10,10)或(﹣5,5).
26.解:∵点P(m+3,m﹣2)在坐标轴上,
∴m+3=0或m﹣2=0,
∴m=﹣3或m=2,
∴点P(0,﹣5)或(5,0).
27.解:(1)以火车站为坐标原点建立的平面直角坐标系如图所示:
(2)体育场(﹣4,3)、宾馆(2,2);
(3)图书馆位置如图所示.
