第4章图形的相似 知识点分类训练 2021-2022学年北师大版九年级数学上册(Word版含答案)
文档属性
| 名称 | 第4章图形的相似 知识点分类训练 2021-2022学年北师大版九年级数学上册(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 941.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-26 16:47:20 | ||
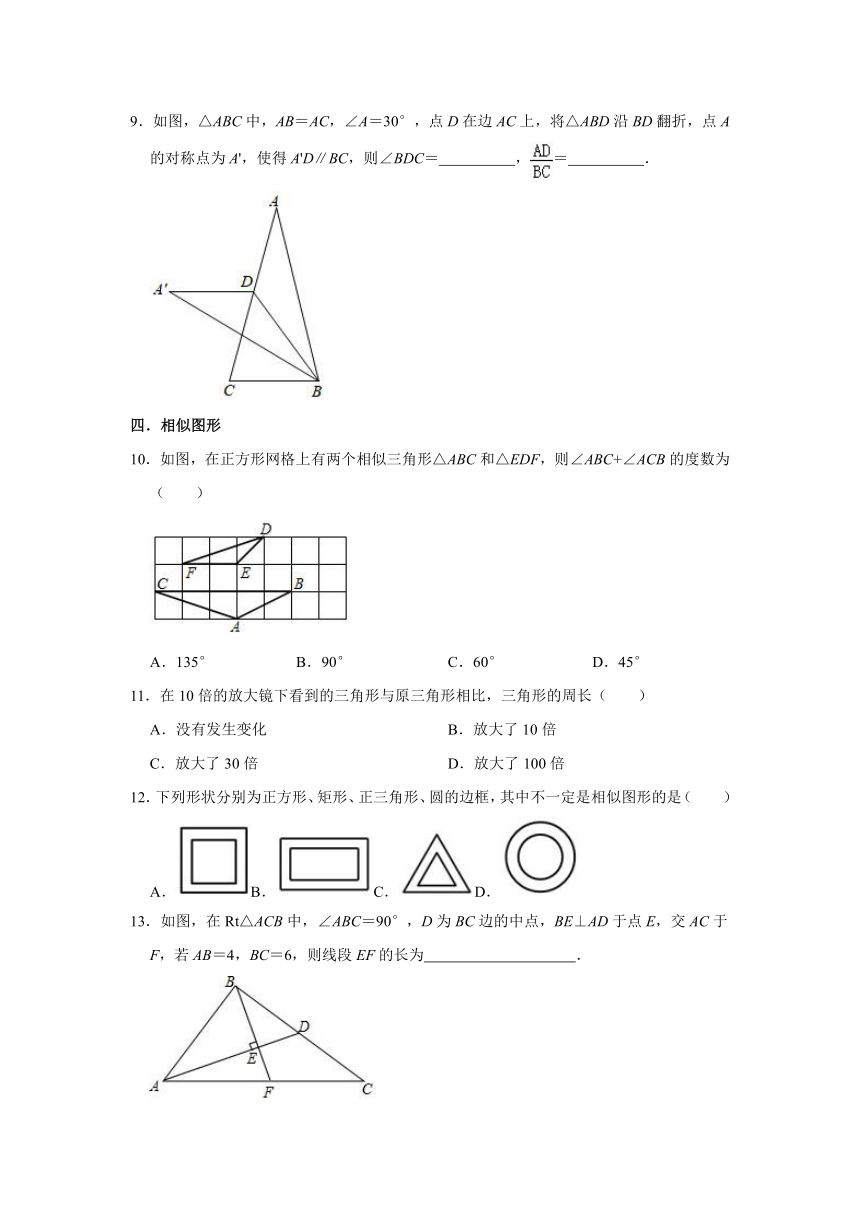
图片预览

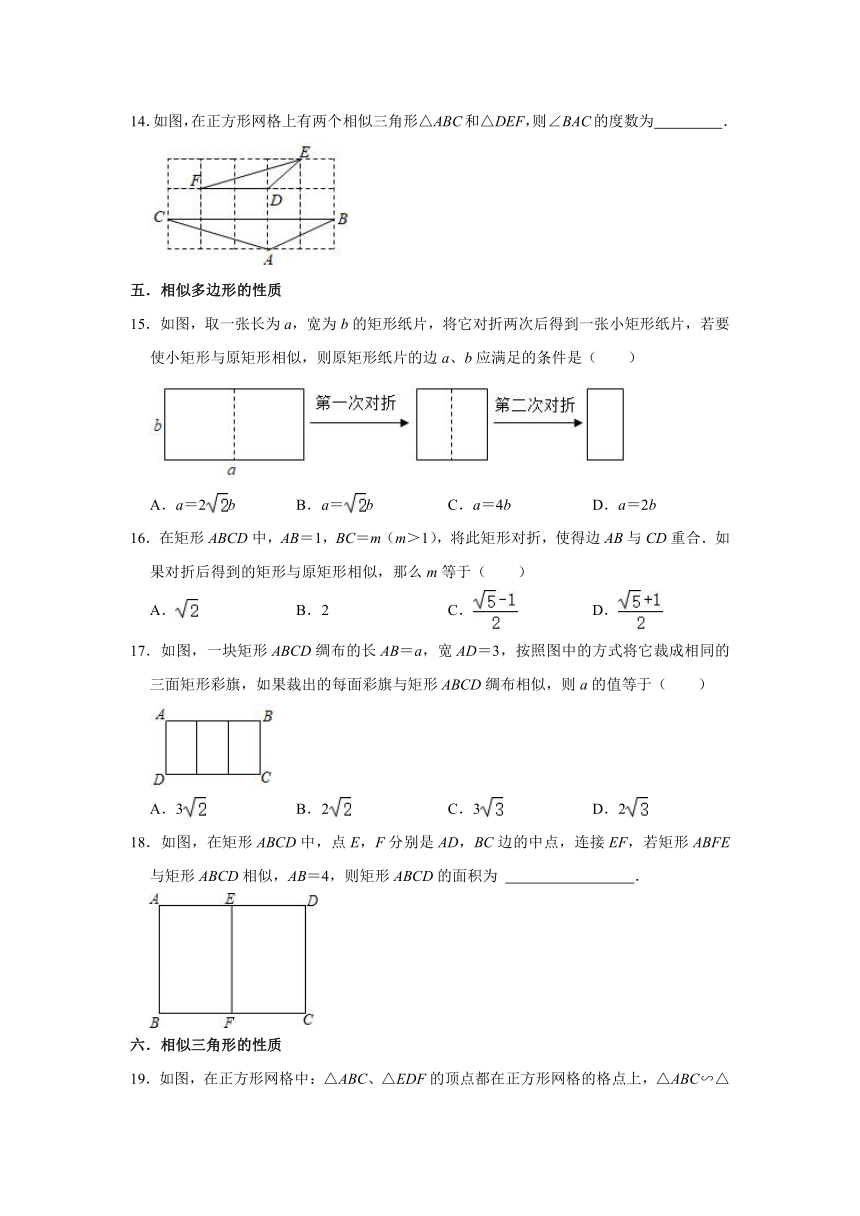
文档简介
2021-2022学年北师大版九年级数学上册《第4章图形的相似》知识点分类训练(附答案)
一.比例的性质
1.如果=,那么的值为( )
A. B. C. D.
2.如果5a=4b,那么= .
二.比例线段
3.下列各组的四条线段a,b,c,d是成比例线段的是( )
A.a=4,b=6,c=5,d=10 B.a=1,b=2,c=3,d=4
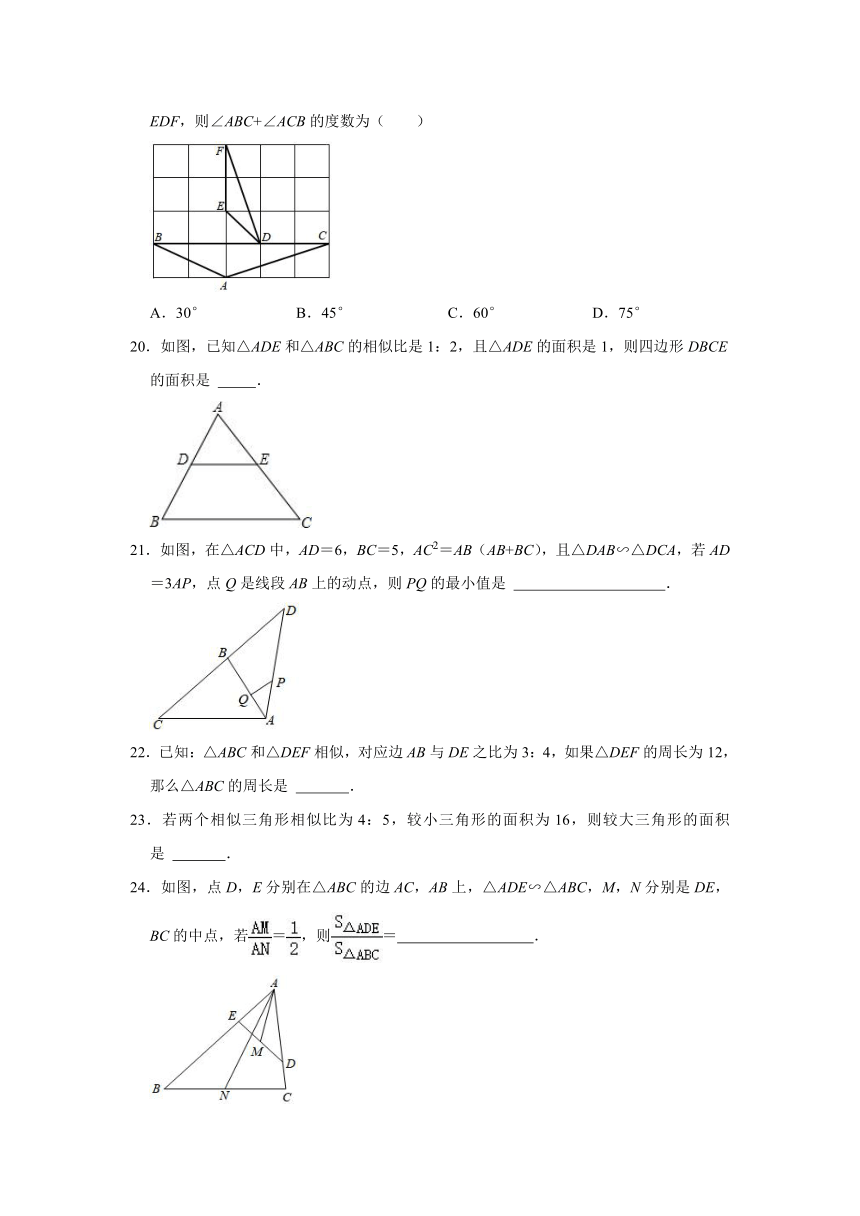
C.,b=3,c=2, D.a=2,,,
4.若==(a≠2c),则= .
5.已知==(b+d≠0),则的值为 .
三.平行线分线段成比例
6.如图,在△ABC中,点D,E、F分别在AB,AC,BC边上,DE∥BC,EF∥AB,则下列式于一定正确的是( )
A. B. C. D.
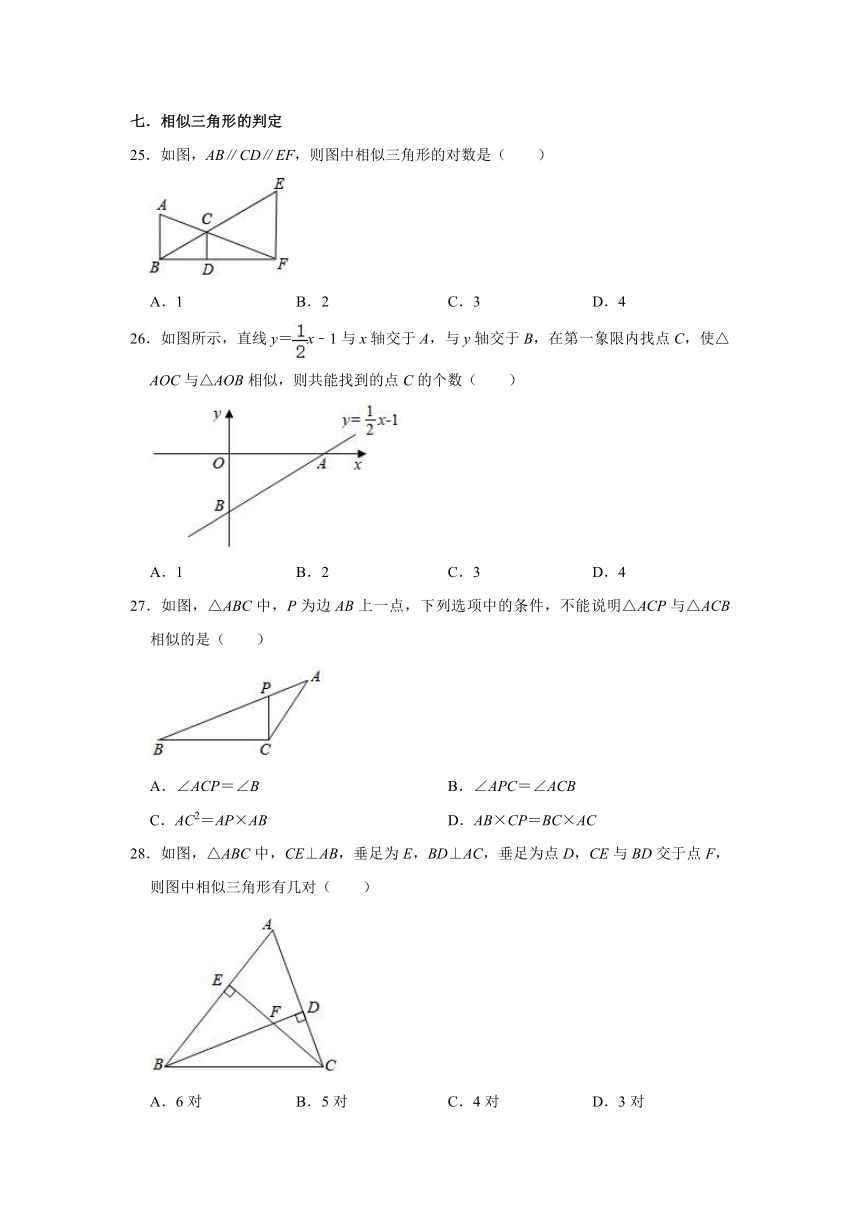
7.如图,两条直线被三条平行直线所截,DE=2,EF=3,AB=1,则AC= .
8.如图,点D、E分别在△ABC的边AB,AC上,DE∥BC,点G在边BC上,AG交DE于点H,点O是线段AG的中点,若AD:DB=3:1,则AO:OH= .
9.如图,△ABC中,AB=AC,∠A=30°,点D在边AC上,将△ABD沿BD翻折,点A的对称点为A',使得A'D∥BC,则∠BDC= ,= .
四.相似图形
10.如图,在正方形网格上有两个相似三角形△ABC和△EDF,则∠ABC+∠ACB的度数为( )
A.135° B.90° C.60° D.45°
11.在10倍的放大镜下看到的三角形与原三角形相比,三角形的周长( )
A.没有发生变化 B.放大了10倍
C.放大了30倍 D.放大了100倍
12.下列形状分别为正方形、矩形、正三角形、圆的边框,其中不一定是相似图形的是( )
A.B.C.D.
13.如图,在Rt△ACB中,∠ABC=90°,D为BC边的中点,BE⊥AD于点E,交AC于F,若AB=4,BC=6,则线段EF的长为 .
14.如图,在正方形网格上有两个相似三角形△ABC和△DEF,则∠BAC的度数为 .
五.相似多边形的性质
15.如图,取一张长为a,宽为b的矩形纸片,将它对折两次后得到一张小矩形纸片,若要使小矩形与原矩形相似,则原矩形纸片的边a、b应满足的条件是( )
A.a=2b B.a=b C.a=4b D.a=2b
16.在矩形ABCD中,AB=1,BC=m(m>1),将此矩形对折,使得边AB与CD重合.如果对折后得到的矩形与原矩形相似,那么m等于( )
A. B.2 C. D.
17.如图,一块矩形ABCD绸布的长AB=a,宽AD=3,按照图中的方式将它裁成相同的三面矩形彩旗,如果裁出的每面彩旗与矩形ABCD绸布相似,则a的值等于( )
A.3 B.2 C.3 D.2
18.如图,在矩形ABCD中,点E,F分别是AD,BC边的中点,连接EF,若矩形ABFE与矩形ABCD相似,AB=4,则矩形ABCD的面积为 .
六.相似三角形的性质
19.如图,在正方形网格中:△ABC、△EDF的顶点都在正方形网格的格点上,△ABC∽△EDF,则∠ABC+∠ACB的度数为( )
A.30° B.45° C.60° D.75°
20.如图,已知△ADE和△ABC的相似比是1:2,且△ADE的面积是1,则四边形DBCE的面积是 .
21.如图,在△ACD中,AD=6,BC=5,AC2=AB(AB+BC),且△DAB∽△DCA,若AD=3AP,点Q是线段AB上的动点,则PQ的最小值是 .
22.已知:△ABC和△DEF相似,对应边AB与DE之比为3:4,如果△DEF的周长为12,那么△ABC的周长是 .
23.若两个相似三角形相似比为4:5,较小三角形的面积为16,则较大三角形的面积是 .
24.如图,点D,E分别在△ABC的边AC,AB上,△ADE∽△ABC,M,N分别是DE,BC的中点,若=,则= .
七.相似三角形的判定
25.如图,AB∥CD∥EF,则图中相似三角形的对数是( )
A.1 B.2 C.3 D.4
26.如图所示,直线y=x﹣1与x轴交于A,与y轴交于B,在第一象限内找点C,使△AOC与△AOB相似,则共能找到的点C的个数( )
A.1 B.2 C.3 D.4
27.如图,△ABC中,P为边AB上一点,下列选项中的条件,不能说明△ACP与△ACB相似的是( )
A.∠ACP=∠B B.∠APC=∠ACB
C.AC2=AP×AB D.AB×CP=BC×AC
28.如图,△ABC中,CE⊥AB,垂足为E,BD⊥AC,垂足为点D,CE与BD交于点F,则图中相似三角形有几对( )
A.6对 B.5对 C.4对 D.3对
29.如图,小正方形的边长均为1,则A、B、C、D四个选项中的三角形(阴影部分)与△ABC相似的是( )
A. B. C. D.
30.在△ABC中,AB=6cm,AC=9cm,动点D从点B开始沿BA边运动,速度为1cm/s;动点E从点A开始沿AC边运动,速度为2cm/s.如果D,E两动点同时运动,那么当它们运动 s时,由D,A,E三点连成的三角形与△ABC相似.
31.如图,在正方形网格中有3个斜三角形:①△ABC;②△CDB;③△DEB;其中能与△ABC相似的是 .(△ABC除外)
32.如图,在平面直角坐标系中,点A(0,6),B(8,0),点C是线段AB的中点,过点C的直线l将△AOB截成两部分,直线l交折线A﹣O﹣B于点P.当截成两部分中有三角形与△AOB相似时,点P的坐标为 .
33.如图△ABC中,AB=6,BC=8,AC=7,点D,E分别在AB,BC上,将△BDE沿ED折叠,点B的对应点F刚好落在AC上.当△CEF与△ABC相似时,BE的长为 .
八.相似三角形的判定与性质
34.如图,在△ABC中,点D、E、F分别在AB、AC、BC上,DE∥BC,DF∥AC.下列比例式中,正确的是( )
A. B. C. D.
35.在△ABC中,D、E分别是边AB与AC的中点,BC=4,下面四个结论:①DE=2;②△ADE∽△ABC;③△ADE的面积与△ABC的面积之比为1:4;④△ADE的周长与△ABC的周长之比为1:4;其中正确的有( )
A.①②④ B.①③④ C.①②③ D.②③④
36.如图,在正方形ABCD中,点E,F,G分别在边BC,CD,DA上,四边形EFGH由两个正方形组成且AB=1,则线段BE的长为( )
A.﹣1 B.3﹣ C. D.
37.如图,正方形ABCD的边长是3,BP=CQ,连接AQ,DP交于点O,并分别与边CD,BC交于点F,E,连接AE,下列结论:①AQ⊥DP;②OA2=OE OP;③S△AOD=S四边形OECF;其中正确结论的个数( )
A.1 B.3 C.2 D.0
38.如图,在Rt△ABC中,∠ACB=90°,以其三边为边向外作正方形,连接CG交AB于点M,连接CE,CH.若CH=2CE,则的值为( )
A. B. C. D.
39.在△ABC中,∠BAC=90°,AD⊥BC,垂足为D,AD=3,BD=2,则CD的长为 .
40.如图,矩形ABCD中,AB=6,BC=8,对角线BD的垂直平分线EF交AD于点E、交BC于点F,则线段EF的长为 .
41.如图,矩形ABCD中,AB=1,AD=2,E为对角线BD上一个动点,过点E作EF⊥AE交BC于F.
(1)当AE=1时,EF的长为 ;
(2)EF长的最小值为 .
42.如图,在Rt△ABC中,∠ACB=90°,D是AB上一点,且AD=,DE∥BC,∠DBE=90°,连接AE.若AC=3,BC=4,则AE的长为 .
43.如图,矩形ABCD中,AB=2,BC=,E为CD中点,连接AE、BD交于点P,连接PC,则PC的长为 .
九.相似三角形的应用
44.图1是装了液体的高脚杯示意图(数据如图),用去一部分液体后如图2所示,此时液面AB=( )
A.1cm B.2cm C.3cm D.4cm
45.如图,点A,B都在格点上,若BC=,则AC的长为( )
A. B. C.2 D.3
46.如图是一块三角形钢材ABC,其中边BC=60cm,高AD=40cm,把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上,则这个正方形零件的边长是( )
A.16 B.24 C.30 D.36
47.如图,小红同学正在使用手电筒进行物理光学实验,地面上从左往右依次是墙、木板和平面镜.手电筒的灯泡位于点G处,手电筒的光从平面镜上点B处反射后,恰好经过木板的边缘点F,落在墙上的点E处.点E到地面的高度ED=3.5m,点F到地面的高度FC=1.5m,灯泡到木板的水平距离AC=5.4m,墙到木板的水平距离为CD=4m.已知光在镜面反射中的入射角等于反射角,图中点A、B、C、D在同一水平面上,则灯泡到地面的高度GA为( )
A.1.2m B.1.3m C.1.4m D.1.5m
48.如图,放映幻灯时,通过光源,把幻灯片上的图形放大到屏幕上.若幻灯片到光源的距离为20cm,到屏幕的距离为40cm,且幻灯片中图形的高度为6cm,则屏幕上图形的高度为 cm.
49.如图,小杰同学跳起来把一个排球打在离他2米(即CO=2米)远的地上,排球反弹碰到墙上,如果他跳起击球时的高度是1.8米(即AC=1.8米),排球落地点离墙的距离是6米(即OD=6米),假设排球一直沿直线运动,那么排球能碰到墙面离地的高度BD的长是 米.
50.在数学活动课上,老师带领数学小组测量大树AB的高度.如图,数学小组发现大树离教学楼有5m,高1.4m的竹竿在水平地面的影子长1m,此时大树的影子有一部分映在地面上,还有一部分映在教学楼的墙上,墙上的影子高CD为2m,那么这棵大树高 m.
十.作图-相似变换
51.如图,方格纸中的每个小正方形的边长都是1,△ABC是格点三角形(顶点在方格顶点处).
(1)在图1中画出一个格点△A1B1C1,使得△A1B1C1与△ABC相似,周长之比为2:1;
(2)在图2中画出一个格点△A2B2C2,使得△A2B2C2与△ABC相似,面积之比为2:1.
52.如图是4×4的正方形网格,△ABC的三个顶点均在格点上.
(1)将△ABC绕点A顺时针方向旋转90°得到△AB1C1,在图①中作出△AB1C1;
(2)在图②中作格点△A2B2C2,使△A2B2C2∽△ABC,且周长比为;
(3)在图③中作一个与△ABC相似且面积最大的格点△A3B3C3
53.如图△ABC,点A,B,C在格点上,试分别在下列两个图中按要求使用无刻度的直尺画图(保留作图痕迹).
(1)在图1中,画出格点△ADE,使△ADE和△ABC相似且相似比为2:1;
(2)在图2中,画出格点△AEF,使△AEF和△ABC相似且面积比为5:2.
十一.位似变换
54.如图,△ABC与△A'B'C'位似,点O是它们的位似中心,其中BC=2B'C',若点A的坐标为(4,2),则A'O的长度为( )
A. B. C. D.
55.如图直角坐标系,△OAB的顶点为O(0,0),A(6,3),B(6,6),以点O为位似中心,在第一象限内作与△OAB的位似比为的位似图形△OCD,则点C的坐标为( )
A.(1,2) B.(2,1) C.(2,2) D.(3,6)
56.如图,在4×7的方格中,点A,B,C,D在格点上,线段CD是由线段AB位似放大得到,则它们的位似中心是( )
A.点P1 B.点P2 C.点P3 D.点P4
57.如图所示是利用图形的位似绘制的一幅“小鱼”图案,其中O为位似中心,且OA=2OD,若图案中鱼身(△ABC)的面积为S,则鱼尾(△DEF)的面积为( )
A. B.S C.S D.S
58.如图,在△AOB中,A,B两点在x轴的上方,以点O为位似中心,在x轴的下方按1:2的相似比作△AOB的位似图形△A'OB'.设点B的对应点B'的坐标是(4,﹣2),则点B的坐标是( )
A.(2,1) B.(2,﹣1) C.(﹣2,1) D.(﹣2,﹣1)
十二.作图-位似变换
59.如图,以点O为位似中心,把△ABC放大2倍得到△A'B'C'',①AB∥A'B';②△ABC∽△A'B'C';③AO:AA'=1:2;④点C、O、C'三点在同一直线上.则以上四种说法正确的是 .
60.如图,△ABC在坐标平面内,三个顶点的坐标分别为A(0,2),B(2,2),C(4,4)(正方形网格中,每个小正方形的边长为1).
(1)画出△ABC关于x轴的对称图形△A1B1C1,并写出点B1的坐标.
(2)以点O为位似中心,在第三象限画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为1:2.
参考答案
一.比例的性质
1.解:设a=5x,则b=3x,
∴==,
故选:B.
2.解:∵5a=4b,
∴.
故答案为:.
二.比例线段
3.解:A.4×10≠6×5,故不符合题意,
B.1×4≠2×3,故不符合题意,
C.,故不符合题意,
D.,故符合题意,
故选:D.
4.解:∵==(a≠2c),
∴==,
∴=.
故答案为:.
5.解:∵==(b+d≠0),
∴=.
故答案为:.
三.平行线分线段成比例
6.解:∵DE∥BC,
∴,
∵EF∥AB,
∴,
∴,
故选:B.
7.解:∵l1∥l2∥l1,
∴=,
∴=,
∴BC=,
∴AC=AB+BC=1+=,
故答案为:.
8.解:∵点O是线段AG的中点,
∴OA=OG=AG,
∵DE∥BC,AD:DB=3:1,
∴===,==,
∴OH=OG﹣HG=AG﹣AG=AG,
∴AO:OH=(AG):(AG)=2:1,
故答案为:2:1.
9.解:方法一:∵AB=AC,∠A=30°,
∴∠ABC=∠C=75°
∵△ABD沿BD翻折,
∴∠A′=∠A=30°,
∵A'D∥BC,
∴∠A′BC=∠A′=30°,
∴∠A′BA=∠ABC﹣∠A′BC=45°,
∵△ABD沿BD翻折,
∴∠DBA=∠DBA′=22.5°,
∴∠BDC=∠A+∠DBA=52.5°;
延长A′D交AB于E,过E作EF⊥A′B于F,如图:
∵AB=AC,A'D∥BC,
∴AD=AE,
∵△ABD沿BD翻折,
∴AD=A′D=A′G=AE,BG=BE,
∵△ABD沿BD翻折,A'D∥BC,
∴∠A=∠A′=∠A′BC=30°,
而∠C=75°,
∴∠BGC=75°,∠EBF=45°,
∴BC=BG=BE,
设AD=A′D=AE=A′G=a,EF=x,
Rt△A′EF中,A′F=x,
Rt△BEF中,BF=x,BE=x,
由AB=A′B可得:a+x=x+x,
解得x=a,
∴BE=BC=x=a,
∴===.
方法二:∵AB=AC,∠A=30°,
∴∠ABC=∠C=75°
∵△ABD沿BD翻折,
∴∠A′=∠A=30°,
∵A'D∥BC,
∴∠A′BC=∠A′=30°,
∴∠A′BA=∠ABC﹣∠A′BC=45°,
∵△ABD沿BD翻折,
∴∠DBA=∠DBA′=22.5°,
∴∠BDC=∠A+∠DBA=52.5°;
过G作GH⊥AB于H,如图:
∵AB=AC,∠A=30°,
∴∠ABC=∠ACB=75°,
∵△ABD沿BD翻折,
∴∠A'=30°,
∵A'D∥BC,
∴∠A'BC=30°,
∴∠ABA'=45°,
∴△BGH是等腰直角三角形,
设GH=BH=m,则BG=m,
∴AH=m,
∴AB=AH+BH=m+m,
∴A'B=AB=m+m,
∴A'G=A'B﹣BG=m+m﹣m,
∵∠ACB=75°,∠A'BC=30°,
∴∠BGC=∠A'GD=75°,
∴BC=BG=m,
∵∠A'=30°,∠A'GD=75°,
∴∠A'DG=75°,
∴A'D=A'G=m+m﹣m,
∴AD=m+m﹣m,
∴==.
故答案为:52.5°,.
四.相似图形
10.解:∵△ABC∽△DEF,
∴∠BAC=∠DEF=180°﹣45°=135°,
∴∠ABC+∠ACB=180°﹣∠BAC=45°.
故选:D.
11.解:在10倍的放大镜下看到的三角形与原三角形相比,则边长扩大10倍,故三角形的周长放大了10倍.
故选:B.
12.解:A、两图形形状相同,是相似图形,不符合题意;
B、两图形形状不同,不是相似图形,符合题意;
C、两图形形状相同,是相似图形,不符合题意;
D、两图形形状相同,是相似图形,不符合题意;
故选:B.
13.解:过点D作DG∥BF交AC于点G,如右图所示,
∵D为BC边的中点,BC=6,
∴BD=3,
∵在Rt△ACB中,∠ABC=90°,AB=4,
∴AD==5,
∵BE⊥AD于点E,交AC于F,
∴BE==,
∵AB=4,BE=,∠AEB=90°,
∴AE==,
设DG=x,则BF=2x,EF=2x﹣,
∵EF∥DG,
∴△AEF∽△ADG,
∴,
即,
解得,x=,
∴EF=2x﹣=2×﹣=,
故答案为:.
14.解:∵△ABC∽△DEF,
∴∠BAC=∠EDF,又∠EDF=90°+45°=135°,
∴∠BAC=135°.
故答案是:135°.
五.相似多边形的性质
15.解:∵小矩形与原矩形相似,原矩形纸片的边长为a、b,
∴=,
∴a2=b2,
∴a2=4b2,
∴a=2b(负数舍去),
故选:D.
16.解:根据矩形相似,对应边的比相等得到:=,
∴=,
∴m2=2,
∵m>0,
∴m=,
故选:A.
17.解:∵使裁出的每面彩旗的宽与长的比与原绸布的宽与长的比相同,
∴,
解得a=3或﹣3(舍弃),
∴a=3,
故选:C.
18.解:设AE=x,则AD=2AE=2x,
∵矩形ABFE与矩形ABCD相似,
∴,即,
解得,x=2,
∴AD=2x=4,
∴矩形ABCD的面积为AB AD=4×4=16,
故答案为:16.
六.相似三角形的性质
19.解:∵△ABC∽△EDF,
∴∠BAC=∠DEF=135°,
∴∠ABC+∠ACB=180°﹣135°=45°,
故选:B.
20.解:∵△ADE和△ABC的相似比是1:2,且△ADE的面积是1,
∴=()2=,
∴S△ABC=4S△ADE=4,
∴S四边形DBCE=S△ABC﹣S△ADE=4﹣1=3.
故答案为:3.
21.解:∵△DAB∽△DCA,
∴,
∴,
解得:BD=4(负值舍去),
∵△DAB∽△DCA,
∴,
∴AC=,
∵AC2=AB(AB+BC),
∴()2=AB(AB+BC),
∴AB=4,
∴AB=BD=4,
过B作BH⊥AD于H,
∴AH=AD=3,
∴BH===,
∵AD=3AP,AD=6,
∴AP=2,
当PQ⊥AB时,PQ的值最小,
∵∠AQP=∠AHB=90°,∠PAQ=∠BAH,
∴△APQ∽△ABH,
∴=,
∴=,
∴PQ=,
故答案为:.
22.解:∵△ABC和△DEF相似,对应边AB与DE之比为3:4,
∴C△ABC:C△DEF=3:4,
∵△DEF的周长是12,
∴C△ABC:12=3:4,
∴△ABC的周长是9,
故答案为:9.
23.解:∵两个相似三角形的相似比是4:5,
∴两个相似三角形的面积比是16:25,
设较大三角形的面积是x.
∵较小三角形的面积为16,
∴16:25=16:x.
解得x=25.
故答案为:25.
24.解:∵M,N分别是DE,BC的中点,
∴AM、AN分别为△ADE、△ABC的中线,
∵△ADE∽△ABC,
∴==,
∴=()2=,
故答案为:.
七.相似三角形的判定
25.解:∵AB∥CD∥EF,
∴△BCD∽△BEF,△FCD∽△FAB,△ABC∽△FEC.
∴图中共有3对相似三角形.
故选:C.
26.解:∵点C在第一象限,
∴当点C为直角顶点时,有两种情形,
当点A为直角顶点时,也有两种情形,共有4种情形.
故选:D.
27.解:A、当∠ACP=∠B,∠A=∠A时,△APC∽△ACB,故本选项不符合题意;
B、当∠APC=∠ACB,∠A=∠A时,△APC∽△ACB,故本选项不符合题意;
C、当AC2=AP AB,即AC:AB=AP:AC时,结合∠A=∠A可以判定△APC∽△ACB,故本选项不符合题意;
D、当AB×CP=AP×AC时,不能判断△APC和△ACB相似.
故选:D.
28.解:∵BD⊥AC,CE⊥AB,
∴∠AEC=∠ADB=90°,∠BEF=∠CDF=90°,
∵∠A=∠A,∠EFB=∠DFC,
∴△AEC∽△ADB,△BEF∽△CDF,
∵∠EBF=∠ABD,∠BEF=∠ADB=90°,
∴△BEF∽△BDA∽△CEA∽△CDF,
∴共有6对相似三角形,
故选:A.
29.解:已知给出的三角形的各边分别为 、2、、
只有选项A的各边为1、、与它的各边对应成比例.
故选:A.
30.解:根据题意得:AE=2t,BD=t,
∴AD=6﹣t,
∵∠A=∠A,
∴分两种情况:
①当=时,
即=,解得:t=;
②当=时,
即=,解得:t=;
综上所述:当t=或时,△ADE与△ABC相似.
31.解:∵△ABC的三边之比是AB:AC:BC=1::,
②△CDB的三边之比是CD:BC:BD=1::;
③△DEB中DE:BD:BE=2:2:=1::.
∴③(△DEB)与△ABC相似,
故答案为:③△DEB.
32.解:当PC∥OB时,△APC∽△AOB,
由点C是AB的中点,可得P为OA的中点,
此时P点坐标为(0,3);
当PC∥OA时,△BCP∽△BAO,
由点C是AB的中点,可得P为OB的中点,
此时P点坐标为(4,0);
当PC⊥AB时,如图,
∵∠CBP=∠OBA,
∴Rt△BPC∽Rt△BAO,
∴=,
∵点B(8,0)和点A(0,6),
∴AB==10,
∵点C是AB的中点,
∴BC=5,
∴=,
∴BP=,
∴OP=OB﹣BP=8﹣=,
此时P点坐标为(,0),
综上所述,满足条件的P点坐标为(0,3)、(4,0)、(,0).
故答案为:(0,3)、(4,0)、(,0).
33.解:∵将△BDE沿DE翻折得到△FDE,
∴BE=EF,
∵BC=8,
∴CE=8﹣BE,
当△CEF与△ABC相似时,=或=,即=或=,
解得:BE=或,
故答案是:或.
八.相似三角形的判定与性质
34.解:∵DE∥BC,
∴△ADE∽△ABC,
∵DF∥AC,
∴△BDF∽△BAC,
∴=,
=,
=,
=,
∴≠,
≠,
≠,
故选:C.
35.解:如图,
在△ABC中,D、E分别是AB、AC的中点
∴DE∥BC,DE=BC=2,
∴△ADE∽△ABC,
故①②正确;
∵△ADE∽△ABC,,
∴△ADE的面积与△ABC的面积之比为 1:4,
△ADE的周长与△ABC的周长之比为 1:2,
故③正确,④错误.
故选:C.
36.解:由题意知,GF=2EF,
∵四边形ABCD是正方形,
∴∠D=∠C=∠B=90°,AB=BC=DC=1.
∵∠DFG+∠CFE=∠CFE+∠CEF=90°,
∴∠DFG=∠CEF,
∴△DFG∽△CEF,
∴=2,
设BE=x,则CE=1﹣x,
∴DF=2CE=2﹣2x,
同理可得△CEF∽△BAE,
∴,
∴,
∴CF=x﹣x2,
∵CD=AB,
∴2﹣2x+x﹣x2=1,
解得x=(负值舍去),
∴BE=.
故选:D.
37.解:∵四边形ABCD是正方形,
∴AD=BC,∠DAB=∠ABC=90°,
∵BP=CQ,
∴AP=BQ,
在△DAP与△ABQ中,
,
∴△DAP≌△ABQ(SAS),
∴∠P=∠Q,
∵∠Q+∠QAB=90°,
∴∠P+∠QAB=90°,
∴∠AOP=90°,
∴AQ⊥DP,故结论①正确;
∵∠DOA=∠AOP=90°,∠ADO+∠P=∠ADO+∠DAO=90°,
∴∠DAO=∠P,
∴△DAO∽△APO,
∴=,
∴AO2=OD OP,
∵AE>AB,
∴AE>AD,
∴OD≠OE,
∴OA2≠OE OP;故结论②错误;
在△CQF与△BPE中,
,
∴△CQF≌△BPE(ASA),
∴CF=BE,
∴DF=CE,
在△ADF与△DCE中,
,
∴△ADF≌△DCE(SAS),
∴S△ADF=S△DCE,
∴S△ADF﹣S△DFO=S△DCE﹣S△DOF,
即S△AOD=S四边形OECF;故结论③正确;
故选:C.
38.解:如图所示,过C作CN⊥AB于N,
由题可得,∠CAE=∠CBH=90°,∠ACE=∠BCH=45°,
∴△ACE∽△BCH,
∴,
设AC=a,则BC=2a,AB=a,CN=a,
Rt△ACN中,AN==a,
∴BN=a﹣a=a,
∵∠CNM=∠GBM=90°,∠CMN=∠GMB,
∴△CNM∽△GBM,
∴,
∴MN=BN=a,BM=NB=a,
∴AM=AN+MN=a,
∴=,
故选:B.
39.解:∵∠BAC=90°,
∴∠BAD+∠DAC=90°,
∵AD⊥BC,
∴∠BAD+∠B=90°,
∴∠B=∠DAC,
∵∠ADB=∠CDA=90°,
∴△ADB∽△CDA,
∴=,即=,
解得:CD=,
故答案为:.
40.解:∵四边形ABCD是矩形,
∴∠A=90°,又AB=6,AD=BC=8,
∴BD==10,
∵EF是BD的垂直平分线,
∴OB=OD=5,∠BOF=90°,又∠C=90°,
∴△BOF∽△BCD,
∴=,
∴=,
解得,OF=,
∵四边形ABCD是矩形,
∴AD∥BC,∠A=90°,
∴∠EDO=∠FBO,
∵EF是BD的垂直平分线,
∴BO=DO,EF⊥BD,
在△DEO和△BFO中,
,
∴△DEO≌△BFO(ASA),
∴OE=OF,
∴EF=2OF=.
故答案为:.
41.解:(1)如图,连接AF交BD于点G,
∵四边形ABCD是矩形,
∴∠ABF=90°,
∵EF⊥AE,
∴∠AEF=90°,
∴∠ABF=∠AEF=90°,
在Rt△ABF和Rt△AEF中,
,
∴Rt△ABF∽Rt△AEF(HL),
∴BF=EF,
∵AB=AE,
∴AF是BE的垂直平分线,
∴∠AGB=90°,
∴∠BAF=∠FBG,
∵AD∥BC,
∴∠ADB=∠FBG,
∴∠ADB=∠BAF,
∴△ABF∽△DAB,
∴=,
∴=,
∴BF=,
∴当AE=1时,EF的长为;
故答案为:;
(2)如图,因为EF⊥AE,
所以当点F与点B重合时,EF长最小,
在矩形ABCD中,
∵AB=1,AD=2,
∴BD==,
∵EF⊥AE,
∴∠AEF=90°,
∴∠BAD=∠AEF=90°,
∵∠DBA=∠AFE,
∴△DBA∽△AFE,
∴=,
∴=,
∴EF=.
故答案为:.
42.解:∵∠ACB=90°,AC=3,BC=4,
∴AB===5,
∵AD=,
∴BD=AB﹣AD=,
∵DE∥BC,
∴∠ABC=∠BDE,
∵∠C=∠DBE=90°,
∴△ACB∽△EBD,
∴=,
∴=,
∴BE=2,
∴AE===,
故答案为:.
43.解:如图,过点P作PQ⊥BC,
∵四边形ABCD是矩形,
∴AB∥CD,AB=CD,AD=BC,∠BAD=90°,
∵E为CD的中点,
∴DE=CD=AB,
∴△ABP∽△EDP,
∴=,
∴=,
∴=,
∵PQ⊥BC,
∴PQ∥CD,
∴△BPQ∽△BDC,
∴==,
∵CD=2,
∴PQ=,
∵AB=2,AD=BC=,
∴BD==,
∴BP=,
∴BQ===,
∴CQ=BC﹣BQ=﹣=,
∴PC===.
故答案为:.
九.相似三角形的应用
44.解:如图:过O作OM⊥CD,垂足为M,过O作ON⊥AB,垂足为N,
∵CD∥AB,
∴△CDO∽ABO,即相似比为,
∴=,
∵OM=15﹣7=8(cm),ON=11﹣7=4(cm),
∴=,
∴AB=3cm,
故选:C.
45.解:作CD⊥BD于点D,作AE⊥BD于点E,如右图所示,
则CD∥AE,
∴△BDC∽△BEA,
∴,
∴=,
解得BA=2,
∴AC=BA﹣BC=2﹣=,
故选:B.
46.解:∵四边形EGHF为正方形,
∴BC∥EF,
∴△AEF∽△ABC;
设正方形零件的边长为x cm,则KD=EF=xcm,AK=(40﹣x)cm,
∵AD⊥BC,
∴=,
∴=,
解得:x=24.
即:正方形零件的边长为24cm.
故选:B.
47.解:由题意可得:FC∥DE,
则△BFC∽△BED,
故=,
即=,
解得:BC=3,
则AB=5.4﹣3=2.4(m),
∵光在镜面反射中的入射角等于反射角,
∴∠FBC=∠GBA,
又∵∠FCB=∠GAB,
∴△BGA∽△BFC,
∴=,
∴=,
解得:AG=1.2(m),
故选:A.
48.解:∵DE∥BC,
∴△AED∽△ABC,
∴,
设屏幕上的小树高是x,
,
解得x=18cm.
故答案为:18.
49.解:由题意得:∠AOC=∠BOD.
∵AC⊥CD,BD⊥CD,
∴∠ACO=∠BDO=90°.
∴△ACO∽△BDO.
∴.
即.
∴BD=5.4(米).
故答案为:5.4.
50.解:如图所示,过D作DE⊥AB于E,
则BE=CD=2(m),DE=BC=5(m).
∵同一时刻物高和影长成正比,
∴=,
∴AE=7m,
∴AB=AE+BE=7+2=9(m),
即:这棵大树高为9m.
故答案为:9.
十.作图-相似变换
51.解:(1)如图,△A1B1C1即为所求作.
(2)如图,△A2B2C2即为所求作.
52.解:(1)如图①中,△AB1C1即为所求作.
(2)如图②中,△A2B2C2即为所求作.
(3)如图③中,△A3B3C3即为所求作.
53.解:(1)如图,△ADE为所作;
(2)如图,△AEF为所作.
十一.位似变换
54.解:∵点A的坐标为(4,2),
∴OA==2,
∵△ABC与△A'B'C'位似,
∴△ABC∽△A'B'C',AC∥A′C′,
∴==,△AOC∽△A'OC',
∴==,
∴A'O=,
故选:B.
55.解:∵以点O为位似中心,在第一象限内作与△OAB的位似比为的位似图形△OCD,A(6,3),
∴点C的坐标为(6×,3×),即(2,1),
故选:B.
56.解:延长CA、DB交于点P1,
则点P1为位似中心,
故选:A.
57.解:∵△ABC与△DEF是以O为位似中心位似图形,OA=2OD,
∴△ABC∽△DEF,且相似比为2,
∴=22=4,
∵△ABC的面积为S,
∴△DEF的面积S,
故选:C.
58.解:设点B的坐标为(x,y),
因为点B的对应点B'的坐标是(4,﹣2),
所以根据位似变换的坐标特点得﹣2 x=4,﹣2 y=﹣2,
即x=﹣2,y=1,故点B的坐标为(﹣2,1).
故选:C.
十二.作图-位似变换
59.解:∵以点O为位似中心,把△ABC放大2倍得到△A'B'C'',
∴AB∥A'B,△ABC∽△A'B'C';AO:AA'=2:1;点C、O、C'三点在同一直线上,
①①②④正确,
故答案为:①②④.
60.解:(1)如图,△A1B1C1为所作,点B1的坐标为(2,﹣2);
(2)如图,△A2B2C2为所作
一.比例的性质
1.如果=,那么的值为( )
A. B. C. D.
2.如果5a=4b,那么= .
二.比例线段
3.下列各组的四条线段a,b,c,d是成比例线段的是( )
A.a=4,b=6,c=5,d=10 B.a=1,b=2,c=3,d=4
C.,b=3,c=2, D.a=2,,,
4.若==(a≠2c),则= .
5.已知==(b+d≠0),则的值为 .
三.平行线分线段成比例
6.如图,在△ABC中,点D,E、F分别在AB,AC,BC边上,DE∥BC,EF∥AB,则下列式于一定正确的是( )
A. B. C. D.
7.如图,两条直线被三条平行直线所截,DE=2,EF=3,AB=1,则AC= .
8.如图,点D、E分别在△ABC的边AB,AC上,DE∥BC,点G在边BC上,AG交DE于点H,点O是线段AG的中点,若AD:DB=3:1,则AO:OH= .
9.如图,△ABC中,AB=AC,∠A=30°,点D在边AC上,将△ABD沿BD翻折,点A的对称点为A',使得A'D∥BC,则∠BDC= ,= .
四.相似图形
10.如图,在正方形网格上有两个相似三角形△ABC和△EDF,则∠ABC+∠ACB的度数为( )
A.135° B.90° C.60° D.45°
11.在10倍的放大镜下看到的三角形与原三角形相比,三角形的周长( )
A.没有发生变化 B.放大了10倍
C.放大了30倍 D.放大了100倍
12.下列形状分别为正方形、矩形、正三角形、圆的边框,其中不一定是相似图形的是( )
A.B.C.D.
13.如图,在Rt△ACB中,∠ABC=90°,D为BC边的中点,BE⊥AD于点E,交AC于F,若AB=4,BC=6,则线段EF的长为 .
14.如图,在正方形网格上有两个相似三角形△ABC和△DEF,则∠BAC的度数为 .
五.相似多边形的性质
15.如图,取一张长为a,宽为b的矩形纸片,将它对折两次后得到一张小矩形纸片,若要使小矩形与原矩形相似,则原矩形纸片的边a、b应满足的条件是( )
A.a=2b B.a=b C.a=4b D.a=2b
16.在矩形ABCD中,AB=1,BC=m(m>1),将此矩形对折,使得边AB与CD重合.如果对折后得到的矩形与原矩形相似,那么m等于( )
A. B.2 C. D.
17.如图,一块矩形ABCD绸布的长AB=a,宽AD=3,按照图中的方式将它裁成相同的三面矩形彩旗,如果裁出的每面彩旗与矩形ABCD绸布相似,则a的值等于( )
A.3 B.2 C.3 D.2
18.如图,在矩形ABCD中,点E,F分别是AD,BC边的中点,连接EF,若矩形ABFE与矩形ABCD相似,AB=4,则矩形ABCD的面积为 .
六.相似三角形的性质
19.如图,在正方形网格中:△ABC、△EDF的顶点都在正方形网格的格点上,△ABC∽△EDF,则∠ABC+∠ACB的度数为( )
A.30° B.45° C.60° D.75°
20.如图,已知△ADE和△ABC的相似比是1:2,且△ADE的面积是1,则四边形DBCE的面积是 .
21.如图,在△ACD中,AD=6,BC=5,AC2=AB(AB+BC),且△DAB∽△DCA,若AD=3AP,点Q是线段AB上的动点,则PQ的最小值是 .
22.已知:△ABC和△DEF相似,对应边AB与DE之比为3:4,如果△DEF的周长为12,那么△ABC的周长是 .
23.若两个相似三角形相似比为4:5,较小三角形的面积为16,则较大三角形的面积是 .
24.如图,点D,E分别在△ABC的边AC,AB上,△ADE∽△ABC,M,N分别是DE,BC的中点,若=,则= .
七.相似三角形的判定
25.如图,AB∥CD∥EF,则图中相似三角形的对数是( )
A.1 B.2 C.3 D.4
26.如图所示,直线y=x﹣1与x轴交于A,与y轴交于B,在第一象限内找点C,使△AOC与△AOB相似,则共能找到的点C的个数( )
A.1 B.2 C.3 D.4
27.如图,△ABC中,P为边AB上一点,下列选项中的条件,不能说明△ACP与△ACB相似的是( )
A.∠ACP=∠B B.∠APC=∠ACB
C.AC2=AP×AB D.AB×CP=BC×AC
28.如图,△ABC中,CE⊥AB,垂足为E,BD⊥AC,垂足为点D,CE与BD交于点F,则图中相似三角形有几对( )
A.6对 B.5对 C.4对 D.3对
29.如图,小正方形的边长均为1,则A、B、C、D四个选项中的三角形(阴影部分)与△ABC相似的是( )
A. B. C. D.
30.在△ABC中,AB=6cm,AC=9cm,动点D从点B开始沿BA边运动,速度为1cm/s;动点E从点A开始沿AC边运动,速度为2cm/s.如果D,E两动点同时运动,那么当它们运动 s时,由D,A,E三点连成的三角形与△ABC相似.
31.如图,在正方形网格中有3个斜三角形:①△ABC;②△CDB;③△DEB;其中能与△ABC相似的是 .(△ABC除外)
32.如图,在平面直角坐标系中,点A(0,6),B(8,0),点C是线段AB的中点,过点C的直线l将△AOB截成两部分,直线l交折线A﹣O﹣B于点P.当截成两部分中有三角形与△AOB相似时,点P的坐标为 .
33.如图△ABC中,AB=6,BC=8,AC=7,点D,E分别在AB,BC上,将△BDE沿ED折叠,点B的对应点F刚好落在AC上.当△CEF与△ABC相似时,BE的长为 .
八.相似三角形的判定与性质
34.如图,在△ABC中,点D、E、F分别在AB、AC、BC上,DE∥BC,DF∥AC.下列比例式中,正确的是( )
A. B. C. D.
35.在△ABC中,D、E分别是边AB与AC的中点,BC=4,下面四个结论:①DE=2;②△ADE∽△ABC;③△ADE的面积与△ABC的面积之比为1:4;④△ADE的周长与△ABC的周长之比为1:4;其中正确的有( )
A.①②④ B.①③④ C.①②③ D.②③④
36.如图,在正方形ABCD中,点E,F,G分别在边BC,CD,DA上,四边形EFGH由两个正方形组成且AB=1,则线段BE的长为( )
A.﹣1 B.3﹣ C. D.
37.如图,正方形ABCD的边长是3,BP=CQ,连接AQ,DP交于点O,并分别与边CD,BC交于点F,E,连接AE,下列结论:①AQ⊥DP;②OA2=OE OP;③S△AOD=S四边形OECF;其中正确结论的个数( )
A.1 B.3 C.2 D.0
38.如图,在Rt△ABC中,∠ACB=90°,以其三边为边向外作正方形,连接CG交AB于点M,连接CE,CH.若CH=2CE,则的值为( )
A. B. C. D.
39.在△ABC中,∠BAC=90°,AD⊥BC,垂足为D,AD=3,BD=2,则CD的长为 .
40.如图,矩形ABCD中,AB=6,BC=8,对角线BD的垂直平分线EF交AD于点E、交BC于点F,则线段EF的长为 .
41.如图,矩形ABCD中,AB=1,AD=2,E为对角线BD上一个动点,过点E作EF⊥AE交BC于F.
(1)当AE=1时,EF的长为 ;
(2)EF长的最小值为 .
42.如图,在Rt△ABC中,∠ACB=90°,D是AB上一点,且AD=,DE∥BC,∠DBE=90°,连接AE.若AC=3,BC=4,则AE的长为 .
43.如图,矩形ABCD中,AB=2,BC=,E为CD中点,连接AE、BD交于点P,连接PC,则PC的长为 .
九.相似三角形的应用
44.图1是装了液体的高脚杯示意图(数据如图),用去一部分液体后如图2所示,此时液面AB=( )
A.1cm B.2cm C.3cm D.4cm
45.如图,点A,B都在格点上,若BC=,则AC的长为( )
A. B. C.2 D.3
46.如图是一块三角形钢材ABC,其中边BC=60cm,高AD=40cm,把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上,则这个正方形零件的边长是( )
A.16 B.24 C.30 D.36
47.如图,小红同学正在使用手电筒进行物理光学实验,地面上从左往右依次是墙、木板和平面镜.手电筒的灯泡位于点G处,手电筒的光从平面镜上点B处反射后,恰好经过木板的边缘点F,落在墙上的点E处.点E到地面的高度ED=3.5m,点F到地面的高度FC=1.5m,灯泡到木板的水平距离AC=5.4m,墙到木板的水平距离为CD=4m.已知光在镜面反射中的入射角等于反射角,图中点A、B、C、D在同一水平面上,则灯泡到地面的高度GA为( )
A.1.2m B.1.3m C.1.4m D.1.5m
48.如图,放映幻灯时,通过光源,把幻灯片上的图形放大到屏幕上.若幻灯片到光源的距离为20cm,到屏幕的距离为40cm,且幻灯片中图形的高度为6cm,则屏幕上图形的高度为 cm.
49.如图,小杰同学跳起来把一个排球打在离他2米(即CO=2米)远的地上,排球反弹碰到墙上,如果他跳起击球时的高度是1.8米(即AC=1.8米),排球落地点离墙的距离是6米(即OD=6米),假设排球一直沿直线运动,那么排球能碰到墙面离地的高度BD的长是 米.
50.在数学活动课上,老师带领数学小组测量大树AB的高度.如图,数学小组发现大树离教学楼有5m,高1.4m的竹竿在水平地面的影子长1m,此时大树的影子有一部分映在地面上,还有一部分映在教学楼的墙上,墙上的影子高CD为2m,那么这棵大树高 m.
十.作图-相似变换
51.如图,方格纸中的每个小正方形的边长都是1,△ABC是格点三角形(顶点在方格顶点处).
(1)在图1中画出一个格点△A1B1C1,使得△A1B1C1与△ABC相似,周长之比为2:1;
(2)在图2中画出一个格点△A2B2C2,使得△A2B2C2与△ABC相似,面积之比为2:1.
52.如图是4×4的正方形网格,△ABC的三个顶点均在格点上.
(1)将△ABC绕点A顺时针方向旋转90°得到△AB1C1,在图①中作出△AB1C1;
(2)在图②中作格点△A2B2C2,使△A2B2C2∽△ABC,且周长比为;
(3)在图③中作一个与△ABC相似且面积最大的格点△A3B3C3
53.如图△ABC,点A,B,C在格点上,试分别在下列两个图中按要求使用无刻度的直尺画图(保留作图痕迹).
(1)在图1中,画出格点△ADE,使△ADE和△ABC相似且相似比为2:1;
(2)在图2中,画出格点△AEF,使△AEF和△ABC相似且面积比为5:2.
十一.位似变换
54.如图,△ABC与△A'B'C'位似,点O是它们的位似中心,其中BC=2B'C',若点A的坐标为(4,2),则A'O的长度为( )
A. B. C. D.
55.如图直角坐标系,△OAB的顶点为O(0,0),A(6,3),B(6,6),以点O为位似中心,在第一象限内作与△OAB的位似比为的位似图形△OCD,则点C的坐标为( )
A.(1,2) B.(2,1) C.(2,2) D.(3,6)
56.如图,在4×7的方格中,点A,B,C,D在格点上,线段CD是由线段AB位似放大得到,则它们的位似中心是( )
A.点P1 B.点P2 C.点P3 D.点P4
57.如图所示是利用图形的位似绘制的一幅“小鱼”图案,其中O为位似中心,且OA=2OD,若图案中鱼身(△ABC)的面积为S,则鱼尾(△DEF)的面积为( )
A. B.S C.S D.S
58.如图,在△AOB中,A,B两点在x轴的上方,以点O为位似中心,在x轴的下方按1:2的相似比作△AOB的位似图形△A'OB'.设点B的对应点B'的坐标是(4,﹣2),则点B的坐标是( )
A.(2,1) B.(2,﹣1) C.(﹣2,1) D.(﹣2,﹣1)
十二.作图-位似变换
59.如图,以点O为位似中心,把△ABC放大2倍得到△A'B'C'',①AB∥A'B';②△ABC∽△A'B'C';③AO:AA'=1:2;④点C、O、C'三点在同一直线上.则以上四种说法正确的是 .
60.如图,△ABC在坐标平面内,三个顶点的坐标分别为A(0,2),B(2,2),C(4,4)(正方形网格中,每个小正方形的边长为1).
(1)画出△ABC关于x轴的对称图形△A1B1C1,并写出点B1的坐标.
(2)以点O为位似中心,在第三象限画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为1:2.
参考答案
一.比例的性质
1.解:设a=5x,则b=3x,
∴==,
故选:B.
2.解:∵5a=4b,
∴.
故答案为:.
二.比例线段
3.解:A.4×10≠6×5,故不符合题意,
B.1×4≠2×3,故不符合题意,
C.,故不符合题意,
D.,故符合题意,
故选:D.
4.解:∵==(a≠2c),
∴==,
∴=.
故答案为:.
5.解:∵==(b+d≠0),
∴=.
故答案为:.
三.平行线分线段成比例
6.解:∵DE∥BC,
∴,
∵EF∥AB,
∴,
∴,
故选:B.
7.解:∵l1∥l2∥l1,
∴=,
∴=,
∴BC=,
∴AC=AB+BC=1+=,
故答案为:.
8.解:∵点O是线段AG的中点,
∴OA=OG=AG,
∵DE∥BC,AD:DB=3:1,
∴===,==,
∴OH=OG﹣HG=AG﹣AG=AG,
∴AO:OH=(AG):(AG)=2:1,
故答案为:2:1.
9.解:方法一:∵AB=AC,∠A=30°,
∴∠ABC=∠C=75°
∵△ABD沿BD翻折,
∴∠A′=∠A=30°,
∵A'D∥BC,
∴∠A′BC=∠A′=30°,
∴∠A′BA=∠ABC﹣∠A′BC=45°,
∵△ABD沿BD翻折,
∴∠DBA=∠DBA′=22.5°,
∴∠BDC=∠A+∠DBA=52.5°;
延长A′D交AB于E,过E作EF⊥A′B于F,如图:
∵AB=AC,A'D∥BC,
∴AD=AE,
∵△ABD沿BD翻折,
∴AD=A′D=A′G=AE,BG=BE,
∵△ABD沿BD翻折,A'D∥BC,
∴∠A=∠A′=∠A′BC=30°,
而∠C=75°,
∴∠BGC=75°,∠EBF=45°,
∴BC=BG=BE,
设AD=A′D=AE=A′G=a,EF=x,
Rt△A′EF中,A′F=x,
Rt△BEF中,BF=x,BE=x,
由AB=A′B可得:a+x=x+x,
解得x=a,
∴BE=BC=x=a,
∴===.
方法二:∵AB=AC,∠A=30°,
∴∠ABC=∠C=75°
∵△ABD沿BD翻折,
∴∠A′=∠A=30°,
∵A'D∥BC,
∴∠A′BC=∠A′=30°,
∴∠A′BA=∠ABC﹣∠A′BC=45°,
∵△ABD沿BD翻折,
∴∠DBA=∠DBA′=22.5°,
∴∠BDC=∠A+∠DBA=52.5°;
过G作GH⊥AB于H,如图:
∵AB=AC,∠A=30°,
∴∠ABC=∠ACB=75°,
∵△ABD沿BD翻折,
∴∠A'=30°,
∵A'D∥BC,
∴∠A'BC=30°,
∴∠ABA'=45°,
∴△BGH是等腰直角三角形,
设GH=BH=m,则BG=m,
∴AH=m,
∴AB=AH+BH=m+m,
∴A'B=AB=m+m,
∴A'G=A'B﹣BG=m+m﹣m,
∵∠ACB=75°,∠A'BC=30°,
∴∠BGC=∠A'GD=75°,
∴BC=BG=m,
∵∠A'=30°,∠A'GD=75°,
∴∠A'DG=75°,
∴A'D=A'G=m+m﹣m,
∴AD=m+m﹣m,
∴==.
故答案为:52.5°,.
四.相似图形
10.解:∵△ABC∽△DEF,
∴∠BAC=∠DEF=180°﹣45°=135°,
∴∠ABC+∠ACB=180°﹣∠BAC=45°.
故选:D.
11.解:在10倍的放大镜下看到的三角形与原三角形相比,则边长扩大10倍,故三角形的周长放大了10倍.
故选:B.
12.解:A、两图形形状相同,是相似图形,不符合题意;
B、两图形形状不同,不是相似图形,符合题意;
C、两图形形状相同,是相似图形,不符合题意;
D、两图形形状相同,是相似图形,不符合题意;
故选:B.
13.解:过点D作DG∥BF交AC于点G,如右图所示,
∵D为BC边的中点,BC=6,
∴BD=3,
∵在Rt△ACB中,∠ABC=90°,AB=4,
∴AD==5,
∵BE⊥AD于点E,交AC于F,
∴BE==,
∵AB=4,BE=,∠AEB=90°,
∴AE==,
设DG=x,则BF=2x,EF=2x﹣,
∵EF∥DG,
∴△AEF∽△ADG,
∴,
即,
解得,x=,
∴EF=2x﹣=2×﹣=,
故答案为:.
14.解:∵△ABC∽△DEF,
∴∠BAC=∠EDF,又∠EDF=90°+45°=135°,
∴∠BAC=135°.
故答案是:135°.
五.相似多边形的性质
15.解:∵小矩形与原矩形相似,原矩形纸片的边长为a、b,
∴=,
∴a2=b2,
∴a2=4b2,
∴a=2b(负数舍去),
故选:D.
16.解:根据矩形相似,对应边的比相等得到:=,
∴=,
∴m2=2,
∵m>0,
∴m=,
故选:A.
17.解:∵使裁出的每面彩旗的宽与长的比与原绸布的宽与长的比相同,
∴,
解得a=3或﹣3(舍弃),
∴a=3,
故选:C.
18.解:设AE=x,则AD=2AE=2x,
∵矩形ABFE与矩形ABCD相似,
∴,即,
解得,x=2,
∴AD=2x=4,
∴矩形ABCD的面积为AB AD=4×4=16,
故答案为:16.
六.相似三角形的性质
19.解:∵△ABC∽△EDF,
∴∠BAC=∠DEF=135°,
∴∠ABC+∠ACB=180°﹣135°=45°,
故选:B.
20.解:∵△ADE和△ABC的相似比是1:2,且△ADE的面积是1,
∴=()2=,
∴S△ABC=4S△ADE=4,
∴S四边形DBCE=S△ABC﹣S△ADE=4﹣1=3.
故答案为:3.
21.解:∵△DAB∽△DCA,
∴,
∴,
解得:BD=4(负值舍去),
∵△DAB∽△DCA,
∴,
∴AC=,
∵AC2=AB(AB+BC),
∴()2=AB(AB+BC),
∴AB=4,
∴AB=BD=4,
过B作BH⊥AD于H,
∴AH=AD=3,
∴BH===,
∵AD=3AP,AD=6,
∴AP=2,
当PQ⊥AB时,PQ的值最小,
∵∠AQP=∠AHB=90°,∠PAQ=∠BAH,
∴△APQ∽△ABH,
∴=,
∴=,
∴PQ=,
故答案为:.
22.解:∵△ABC和△DEF相似,对应边AB与DE之比为3:4,
∴C△ABC:C△DEF=3:4,
∵△DEF的周长是12,
∴C△ABC:12=3:4,
∴△ABC的周长是9,
故答案为:9.
23.解:∵两个相似三角形的相似比是4:5,
∴两个相似三角形的面积比是16:25,
设较大三角形的面积是x.
∵较小三角形的面积为16,
∴16:25=16:x.
解得x=25.
故答案为:25.
24.解:∵M,N分别是DE,BC的中点,
∴AM、AN分别为△ADE、△ABC的中线,
∵△ADE∽△ABC,
∴==,
∴=()2=,
故答案为:.
七.相似三角形的判定
25.解:∵AB∥CD∥EF,
∴△BCD∽△BEF,△FCD∽△FAB,△ABC∽△FEC.
∴图中共有3对相似三角形.
故选:C.
26.解:∵点C在第一象限,
∴当点C为直角顶点时,有两种情形,
当点A为直角顶点时,也有两种情形,共有4种情形.
故选:D.
27.解:A、当∠ACP=∠B,∠A=∠A时,△APC∽△ACB,故本选项不符合题意;
B、当∠APC=∠ACB,∠A=∠A时,△APC∽△ACB,故本选项不符合题意;
C、当AC2=AP AB,即AC:AB=AP:AC时,结合∠A=∠A可以判定△APC∽△ACB,故本选项不符合题意;
D、当AB×CP=AP×AC时,不能判断△APC和△ACB相似.
故选:D.
28.解:∵BD⊥AC,CE⊥AB,
∴∠AEC=∠ADB=90°,∠BEF=∠CDF=90°,
∵∠A=∠A,∠EFB=∠DFC,
∴△AEC∽△ADB,△BEF∽△CDF,
∵∠EBF=∠ABD,∠BEF=∠ADB=90°,
∴△BEF∽△BDA∽△CEA∽△CDF,
∴共有6对相似三角形,
故选:A.
29.解:已知给出的三角形的各边分别为 、2、、
只有选项A的各边为1、、与它的各边对应成比例.
故选:A.
30.解:根据题意得:AE=2t,BD=t,
∴AD=6﹣t,
∵∠A=∠A,
∴分两种情况:
①当=时,
即=,解得:t=;
②当=时,
即=,解得:t=;
综上所述:当t=或时,△ADE与△ABC相似.
31.解:∵△ABC的三边之比是AB:AC:BC=1::,
②△CDB的三边之比是CD:BC:BD=1::;
③△DEB中DE:BD:BE=2:2:=1::.
∴③(△DEB)与△ABC相似,
故答案为:③△DEB.
32.解:当PC∥OB时,△APC∽△AOB,
由点C是AB的中点,可得P为OA的中点,
此时P点坐标为(0,3);
当PC∥OA时,△BCP∽△BAO,
由点C是AB的中点,可得P为OB的中点,
此时P点坐标为(4,0);
当PC⊥AB时,如图,
∵∠CBP=∠OBA,
∴Rt△BPC∽Rt△BAO,
∴=,
∵点B(8,0)和点A(0,6),
∴AB==10,
∵点C是AB的中点,
∴BC=5,
∴=,
∴BP=,
∴OP=OB﹣BP=8﹣=,
此时P点坐标为(,0),
综上所述,满足条件的P点坐标为(0,3)、(4,0)、(,0).
故答案为:(0,3)、(4,0)、(,0).
33.解:∵将△BDE沿DE翻折得到△FDE,
∴BE=EF,
∵BC=8,
∴CE=8﹣BE,
当△CEF与△ABC相似时,=或=,即=或=,
解得:BE=或,
故答案是:或.
八.相似三角形的判定与性质
34.解:∵DE∥BC,
∴△ADE∽△ABC,
∵DF∥AC,
∴△BDF∽△BAC,
∴=,
=,
=,
=,
∴≠,
≠,
≠,
故选:C.
35.解:如图,
在△ABC中,D、E分别是AB、AC的中点
∴DE∥BC,DE=BC=2,
∴△ADE∽△ABC,
故①②正确;
∵△ADE∽△ABC,,
∴△ADE的面积与△ABC的面积之比为 1:4,
△ADE的周长与△ABC的周长之比为 1:2,
故③正确,④错误.
故选:C.
36.解:由题意知,GF=2EF,
∵四边形ABCD是正方形,
∴∠D=∠C=∠B=90°,AB=BC=DC=1.
∵∠DFG+∠CFE=∠CFE+∠CEF=90°,
∴∠DFG=∠CEF,
∴△DFG∽△CEF,
∴=2,
设BE=x,则CE=1﹣x,
∴DF=2CE=2﹣2x,
同理可得△CEF∽△BAE,
∴,
∴,
∴CF=x﹣x2,
∵CD=AB,
∴2﹣2x+x﹣x2=1,
解得x=(负值舍去),
∴BE=.
故选:D.
37.解:∵四边形ABCD是正方形,
∴AD=BC,∠DAB=∠ABC=90°,
∵BP=CQ,
∴AP=BQ,
在△DAP与△ABQ中,
,
∴△DAP≌△ABQ(SAS),
∴∠P=∠Q,
∵∠Q+∠QAB=90°,
∴∠P+∠QAB=90°,
∴∠AOP=90°,
∴AQ⊥DP,故结论①正确;
∵∠DOA=∠AOP=90°,∠ADO+∠P=∠ADO+∠DAO=90°,
∴∠DAO=∠P,
∴△DAO∽△APO,
∴=,
∴AO2=OD OP,
∵AE>AB,
∴AE>AD,
∴OD≠OE,
∴OA2≠OE OP;故结论②错误;
在△CQF与△BPE中,
,
∴△CQF≌△BPE(ASA),
∴CF=BE,
∴DF=CE,
在△ADF与△DCE中,
,
∴△ADF≌△DCE(SAS),
∴S△ADF=S△DCE,
∴S△ADF﹣S△DFO=S△DCE﹣S△DOF,
即S△AOD=S四边形OECF;故结论③正确;
故选:C.
38.解:如图所示,过C作CN⊥AB于N,
由题可得,∠CAE=∠CBH=90°,∠ACE=∠BCH=45°,
∴△ACE∽△BCH,
∴,
设AC=a,则BC=2a,AB=a,CN=a,
Rt△ACN中,AN==a,
∴BN=a﹣a=a,
∵∠CNM=∠GBM=90°,∠CMN=∠GMB,
∴△CNM∽△GBM,
∴,
∴MN=BN=a,BM=NB=a,
∴AM=AN+MN=a,
∴=,
故选:B.
39.解:∵∠BAC=90°,
∴∠BAD+∠DAC=90°,
∵AD⊥BC,
∴∠BAD+∠B=90°,
∴∠B=∠DAC,
∵∠ADB=∠CDA=90°,
∴△ADB∽△CDA,
∴=,即=,
解得:CD=,
故答案为:.
40.解:∵四边形ABCD是矩形,
∴∠A=90°,又AB=6,AD=BC=8,
∴BD==10,
∵EF是BD的垂直平分线,
∴OB=OD=5,∠BOF=90°,又∠C=90°,
∴△BOF∽△BCD,
∴=,
∴=,
解得,OF=,
∵四边形ABCD是矩形,
∴AD∥BC,∠A=90°,
∴∠EDO=∠FBO,
∵EF是BD的垂直平分线,
∴BO=DO,EF⊥BD,
在△DEO和△BFO中,
,
∴△DEO≌△BFO(ASA),
∴OE=OF,
∴EF=2OF=.
故答案为:.
41.解:(1)如图,连接AF交BD于点G,
∵四边形ABCD是矩形,
∴∠ABF=90°,
∵EF⊥AE,
∴∠AEF=90°,
∴∠ABF=∠AEF=90°,
在Rt△ABF和Rt△AEF中,
,
∴Rt△ABF∽Rt△AEF(HL),
∴BF=EF,
∵AB=AE,
∴AF是BE的垂直平分线,
∴∠AGB=90°,
∴∠BAF=∠FBG,
∵AD∥BC,
∴∠ADB=∠FBG,
∴∠ADB=∠BAF,
∴△ABF∽△DAB,
∴=,
∴=,
∴BF=,
∴当AE=1时,EF的长为;
故答案为:;
(2)如图,因为EF⊥AE,
所以当点F与点B重合时,EF长最小,
在矩形ABCD中,
∵AB=1,AD=2,
∴BD==,
∵EF⊥AE,
∴∠AEF=90°,
∴∠BAD=∠AEF=90°,
∵∠DBA=∠AFE,
∴△DBA∽△AFE,
∴=,
∴=,
∴EF=.
故答案为:.
42.解:∵∠ACB=90°,AC=3,BC=4,
∴AB===5,
∵AD=,
∴BD=AB﹣AD=,
∵DE∥BC,
∴∠ABC=∠BDE,
∵∠C=∠DBE=90°,
∴△ACB∽△EBD,
∴=,
∴=,
∴BE=2,
∴AE===,
故答案为:.
43.解:如图,过点P作PQ⊥BC,
∵四边形ABCD是矩形,
∴AB∥CD,AB=CD,AD=BC,∠BAD=90°,
∵E为CD的中点,
∴DE=CD=AB,
∴△ABP∽△EDP,
∴=,
∴=,
∴=,
∵PQ⊥BC,
∴PQ∥CD,
∴△BPQ∽△BDC,
∴==,
∵CD=2,
∴PQ=,
∵AB=2,AD=BC=,
∴BD==,
∴BP=,
∴BQ===,
∴CQ=BC﹣BQ=﹣=,
∴PC===.
故答案为:.
九.相似三角形的应用
44.解:如图:过O作OM⊥CD,垂足为M,过O作ON⊥AB,垂足为N,
∵CD∥AB,
∴△CDO∽ABO,即相似比为,
∴=,
∵OM=15﹣7=8(cm),ON=11﹣7=4(cm),
∴=,
∴AB=3cm,
故选:C.
45.解:作CD⊥BD于点D,作AE⊥BD于点E,如右图所示,
则CD∥AE,
∴△BDC∽△BEA,
∴,
∴=,
解得BA=2,
∴AC=BA﹣BC=2﹣=,
故选:B.
46.解:∵四边形EGHF为正方形,
∴BC∥EF,
∴△AEF∽△ABC;
设正方形零件的边长为x cm,则KD=EF=xcm,AK=(40﹣x)cm,
∵AD⊥BC,
∴=,
∴=,
解得:x=24.
即:正方形零件的边长为24cm.
故选:B.
47.解:由题意可得:FC∥DE,
则△BFC∽△BED,
故=,
即=,
解得:BC=3,
则AB=5.4﹣3=2.4(m),
∵光在镜面反射中的入射角等于反射角,
∴∠FBC=∠GBA,
又∵∠FCB=∠GAB,
∴△BGA∽△BFC,
∴=,
∴=,
解得:AG=1.2(m),
故选:A.
48.解:∵DE∥BC,
∴△AED∽△ABC,
∴,
设屏幕上的小树高是x,
,
解得x=18cm.
故答案为:18.
49.解:由题意得:∠AOC=∠BOD.
∵AC⊥CD,BD⊥CD,
∴∠ACO=∠BDO=90°.
∴△ACO∽△BDO.
∴.
即.
∴BD=5.4(米).
故答案为:5.4.
50.解:如图所示,过D作DE⊥AB于E,
则BE=CD=2(m),DE=BC=5(m).
∵同一时刻物高和影长成正比,
∴=,
∴AE=7m,
∴AB=AE+BE=7+2=9(m),
即:这棵大树高为9m.
故答案为:9.
十.作图-相似变换
51.解:(1)如图,△A1B1C1即为所求作.
(2)如图,△A2B2C2即为所求作.
52.解:(1)如图①中,△AB1C1即为所求作.
(2)如图②中,△A2B2C2即为所求作.
(3)如图③中,△A3B3C3即为所求作.
53.解:(1)如图,△ADE为所作;
(2)如图,△AEF为所作.
十一.位似变换
54.解:∵点A的坐标为(4,2),
∴OA==2,
∵△ABC与△A'B'C'位似,
∴△ABC∽△A'B'C',AC∥A′C′,
∴==,△AOC∽△A'OC',
∴==,
∴A'O=,
故选:B.
55.解:∵以点O为位似中心,在第一象限内作与△OAB的位似比为的位似图形△OCD,A(6,3),
∴点C的坐标为(6×,3×),即(2,1),
故选:B.
56.解:延长CA、DB交于点P1,
则点P1为位似中心,
故选:A.
57.解:∵△ABC与△DEF是以O为位似中心位似图形,OA=2OD,
∴△ABC∽△DEF,且相似比为2,
∴=22=4,
∵△ABC的面积为S,
∴△DEF的面积S,
故选:C.
58.解:设点B的坐标为(x,y),
因为点B的对应点B'的坐标是(4,﹣2),
所以根据位似变换的坐标特点得﹣2 x=4,﹣2 y=﹣2,
即x=﹣2,y=1,故点B的坐标为(﹣2,1).
故选:C.
十二.作图-位似变换
59.解:∵以点O为位似中心,把△ABC放大2倍得到△A'B'C'',
∴AB∥A'B,△ABC∽△A'B'C';AO:AA'=2:1;点C、O、C'三点在同一直线上,
①①②④正确,
故答案为:①②④.
60.解:(1)如图,△A1B1C1为所作,点B1的坐标为(2,﹣2);
(2)如图,△A2B2C2为所作
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
