4.6利用相似三角形测高 解答题专题提升训练 2021-2022学年北师大版九年级数学上册(Word版含答案)
文档属性
| 名称 | 4.6利用相似三角形测高 解答题专题提升训练 2021-2022学年北师大版九年级数学上册(Word版含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 365.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-27 00:00:00 | ||
图片预览



文档简介
2021-2022学年北师大版九年级数学上册《4.6利用相似三角形测高》
解答题专题提升训练(附答案)
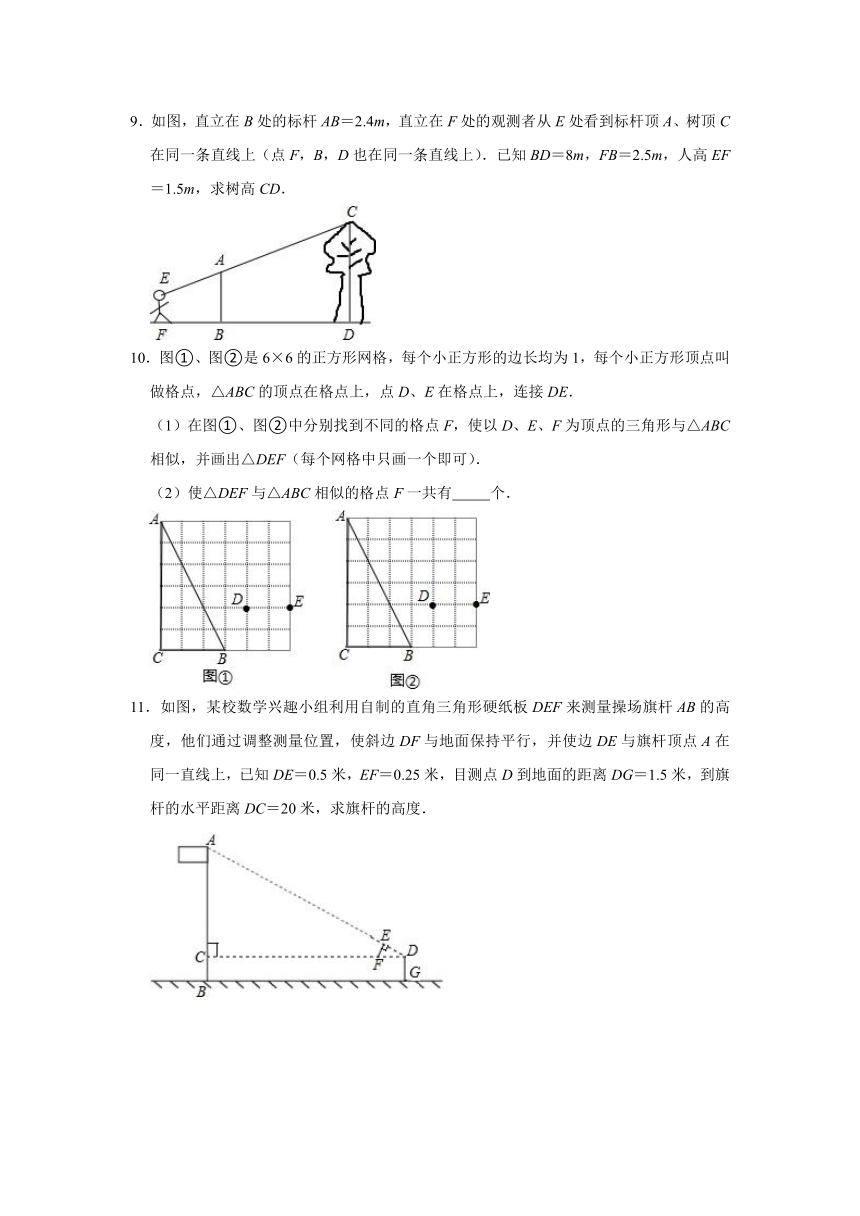
1.如图,为了估算河的宽度,我们可以在河对岸选定一点A,再在河的这一边选定点B和点C,使得AB⊥BC,然后选定点E,使EC⊥BC,确定BC与AE的交点为D,若测得BD=180m,DC=60m,EC=50m,你能知道小河的宽是多少吗?
2.如图,△ABC是一块锐角三角形余料,边长BC=120cm,高AP=90cm,现在要把它加工成长方形零件DFHE,且满足FH=2DF,F、H在BC上,D、E分别在AB、AC上,求短边DF的长.
3.如图,利用标杆BE测量建筑物的高度,如果标杆BE高1.2m,测得AB=1.6m,BC=12.4m,楼高CD是多少?
4.如图,AB是斜靠在墙壁上的长梯,梯脚B距墙80cm,梯上点D距墙70cm,BD长55cm,求梯子的长.
5.一块材料的形状是锐角三角形ABC,边BC=120mm,高AD=80mm,把它加工成正方形零件如图,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.
(1)求证:△AEF∽△ABC;
(2)求这个正方形零件的边长.
6.如图,直立在点B处的标杆AB长2.5m,站立在点F处的观察者从点E处看到标杆顶A、树顶C在一条直线上.已知BD=10m,FB=3m,人目高EF=1.7m,求树高DC(精确到0.1m)
7.一块直角三角形木板,它的一条直角边AB长1.5m,面积为1.5m2.甲、乙两位木匠分别按图①、②把它加工成一个正方形桌面.请说明哪个正方形面积较大(加工损耗不计).
8.如图,要测量湖岸AB之间的距离,在与湖岸平行的公路上选择两点C、D,确定AD与BC交于点O,测得CD为75m,CO为45m,BO为60m,求湖面AB之间的距离.
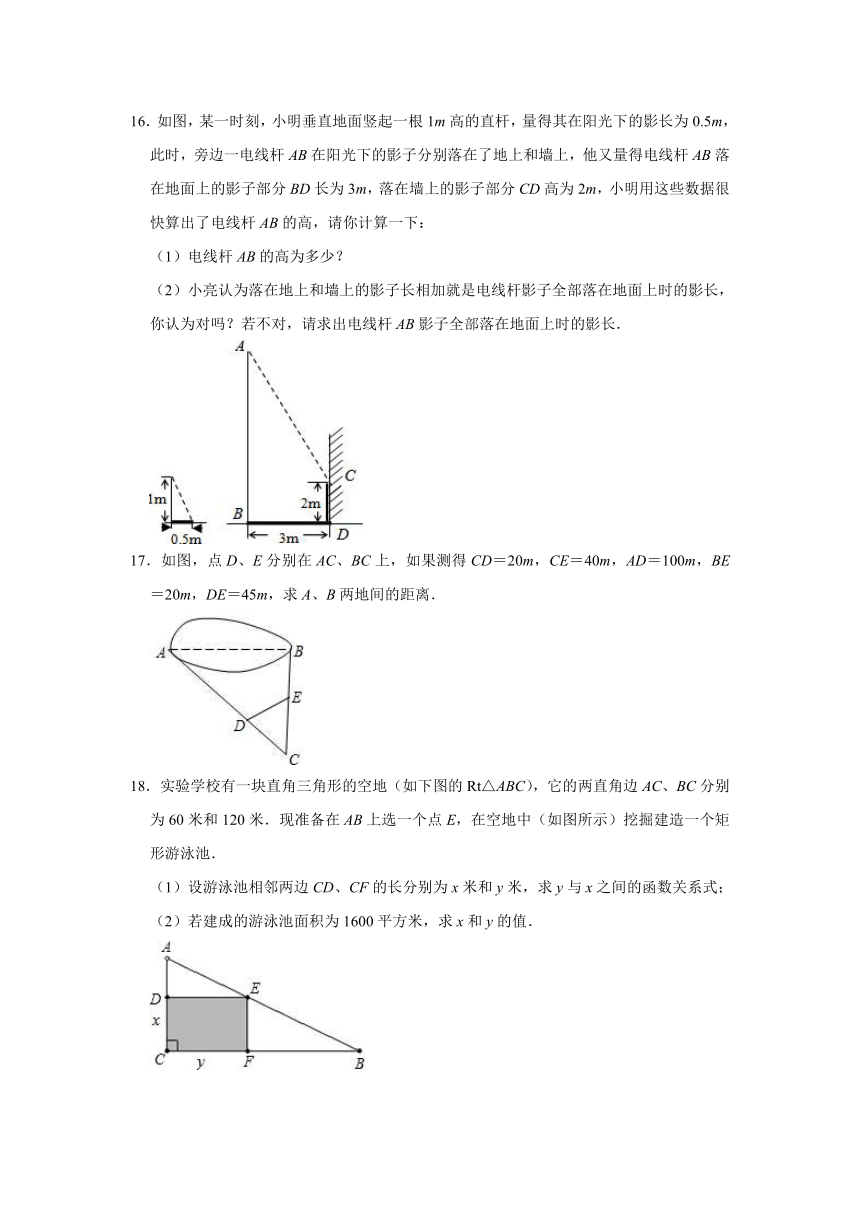
9.如图,直立在B处的标杆AB=2.4m,直立在F处的观测者从E处看到标杆顶A、树顶C在同一条直线上(点F,B,D也在同一条直线上).已知BD=8m,FB=2.5m,人高EF=1.5m,求树高CD.
10.图①、图②是6×6的正方形网格,每个小正方形的边长均为1,每个小正方形顶点叫做格点,△ABC的顶点在格点上,点D、E在格点上,连接DE.
(1)在图①、图②中分别找到不同的格点F,使以D、E、F为顶点的三角形与△ABC相似,并画出△DEF(每个网格中只画一个即可).
(2)使△DEF与△ABC相似的格点F一共有 个.
11.如图,某校数学兴趣小组利用自制的直角三角形硬纸板DEF来测量操场旗杆AB的高度,他们通过调整测量位置,使斜边DF与地面保持平行,并使边DE与旗杆顶点A在同一直线上,已知DE=0.5米,EF=0.25米,目测点D到地面的距离DG=1.5米,到旗杆的水平距离DC=20米,求旗杆的高度.
12.如图,矩形ABCD为台球桌面,AD=260cm,AB=130cm,球目前在E点位置,AE=60cm.如果小丁瞄准BC边上的点F将球打过去,经过反弹后,球刚好弹到D点位置.
(1)求证:△BEF∽△CDF;
(2)求CF的长.
13.已知:如图是一束光线射入室内的平面图,上檐边缘射入的光线照在距窗户2.5m处,已知窗户AB高为2m,B点距地面高为1.2m,求下檐光线的落地点N与窗户的距离NC.
如图,零件的外径为16cm,要求它的壁厚x,需要先求出内径AB,现用一个交叉钳(AD与BC相等)去量,若测得OA:OD=OB:OC=3:1,CD=5cm,求零件的壁厚x?
15.如图,是一个照相机成像的示意图.
(1)如果像高MN是35mm,焦距是50mm,拍摄的景物高度AB是4.9m,拍摄点离景物有多远?
(2)如果要完整的拍摄高度是2m的景物,拍摄点离景物有4m,像高不变,则相机的焦距应调整为多少?
16.如图,某一时刻,小明垂直地面竖起一根1m高的直杆,量得其在阳光下的影长为0.5m,此时,旁边一电线杆AB在阳光下的影子分别落在了地上和墙上,他又量得电线杆AB落在地面上的影子部分BD长为3m,落在墙上的影子部分CD高为2m,小明用这些数据很快算出了电线杆AB的高,请你计算一下:
(1)电线杆AB的高为多少?
(2)小亮认为落在地上和墙上的影子长相加就是电线杆影子全部落在地面上时的影长,你认为对吗?若不对,请求出电线杆AB影子全部落在地面上时的影长.
17.如图,点D、E分别在AC、BC上,如果测得CD=20m,CE=40m,AD=100m,BE=20m,DE=45m,求A、B两地间的距离.
18.实验学校有一块直角三角形的空地(如下图的Rt△ABC),它的两直角边AC、BC分别为60米和120米.现准备在AB上选一个点E,在空地中(如图所示)挖掘建造一个矩形游泳池.
(1)设游泳池相邻两边CD、CF的长分别为x米和y米,求y与x之间的函数关系式;
(2)若建成的游泳池面积为1600平方米,求x和y的值.
19.如图所示,在离某建筑物4m处有一棵树,在某时刻,1.2m长的竹竿垂直地面,影长为2m,此时,树的影子有一部分映在地面上,还有一部分影子映在建筑物的墙上,墙上的影高为2m,那么这棵树高约有多少米?
20.教学楼旁边有一棵树,学习了相似三角形后,数学小组的同学想利用树影来测量树高.课外活动时在阳光下他们测得一根长为1m的竹竿的影长是0.9m,但当他们马上测量树高时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上,经过一番争论,小组的同学认为继续测量也可以测出树高,他们测得落在地面的影长2.7m,落在墙壁上的影长1.2m,请你和他们一起算一下,树高为多少?
21.小玲用下面的方法来测量学校教学大楼AB的高度:如图,在水平地面上放一面平面镜,镜子与教学大楼的距离EA=21米.当她与镜子的距离CE=2.5米时,她刚好能从镜子中看到教学大楼的顶端B.已知她的眼睛距地面高度DC=1.6米.请你帮助小玲计算出教学大楼的高度AB是多少米?(注意:根据光的反射定律:反射角等于入射角).
22.夜晚,小明在路灯下散步.若小明身高1.5m,路灯的灯柱高4.5m.
(1)如图1,若小明在相距10米的两路灯AB、CD之间行走(不含两端),他在路灯AB下的影子为FM,在路灯CD下的影子为FN.解答问题:
①若BF=4,求影子FM.②猜想影子FM与FN的长的和为定值吗?说出理由.
(2)有言道:形影不离.其原意为:人的影子与自己紧密相伴,无法分离.但在灯光下,人的速度与影子的速度却不是一样的!如图2,若小明在灯柱PQ前,朝着影子的方向(如图箭头),以0.8米/秒的速度匀速行走,试求他影子的顶端R在地面上移动的速度.
23.如图,路灯(P点)距地面8米,身高1.6米的小明从距路灯的底部(O点)20米的A点,沿OA所在的直线行走14米到B点时,身影的长度是变长了还是变短了?变长或变短了多少米?
24.九年级(1)班课外活动小组利用标杆测量学校旗杆的高度,已知标杆高度CD=3m,标杆与旗杆的水平距离BD=15m,人的眼睛与地面的高度EF=1.6m,人与标杆CD的水平距离DF=2m,求旗杆AB的高度.
参考答案
1.解:由已知得,∠ABD=∠DCE=90°,∠ADB=∠CDE,
∴△ABD∽△ECD,
∴=,
将BD=180m,DC=60m,EC=50m,代入可得:=,
解得:AB=150.
答:小河的宽是150m.
2.解:设DF=xcm,
则DE=2xcm,AK=(90﹣x)cm,
∵DE∥BC,
∴△ADE∽△ABC,
∴=,
∴,
∴x=36,
∴DF的长为36cm.
3.解:∵EB⊥AC,DC⊥AC,
∴EB∥DC,
∴△ABE∽△ACD,
∴=,
∵BE=1.2,AB=1.6,BC=12.4,
∴AC=14,
∴=,
∴CD=10.5.
答:楼高CD是10.5m.
4.解:∵DE⊥AC,BC⊥AC,
∴DE∥BC.
∴△ADE∽△ABC.
∴AD:AB=DE:BC.
∴(AB﹣55):AB=70:80.
∴AB=440cm.
∴梯子长为440cm.
5.(1)证明:∵四边形EFHG是正方形,
∴EF∥BC,
∴△AEF∽△ABC.
(2)解:设这个正方形零件的边长是xmm,
∵EF∥BC,
∴=,
∴=,
解得x=48
答:这个正方形零件的边长是48mm.
6.解:过E作EH⊥CD交CD于H点,交AB于点G,如下图所示:
由已知得,EF⊥FD,AB⊥FD,CD⊥FD,
∵EH⊥CD,EH⊥AB
∴四边形EFDH为矩形
∴EF=GB=DH=1.7,EG=FB=3,GH=BD=10
∴AG=AB﹣GB=0.8
∵EH⊥CD,EH⊥AB,
∴AG∥CH,
∴△AEG∽△CEH
∴
∵EH=EG+GH=13
∴CH=≈3.5
∴CD=CH+HD=5.2
答:故树高DC为5.2米.
7.解:由AB=1.5m,S△ABC=1.5m2,可得BC=2m,
由图①,过点B作Rt△ABC斜边AC上的高,BH交DE于P,交AC于H.
由AB=1.5m,BC=2m,
得AC=(m),
由AC BH=AB BC 可得:BH==1.2(m),
设甲设计的桌面的边长为xm,
∵DE∥AC,
∴Rt△BDE∽Rt△BAC,
∴,即,
解得(m),
由图②,若设乙设计的正方形桌面边长为ym,
由DE∥AB,得Rt△CDE∽Rt△CBA,
∴,即,
解得(m),
∵,,
∴x<y,即x2<y2,
∴S正方形①<S正方形②,
∴第二个正方形面积大.
8.解:∵AB∥CD,
∴∠A=∠D,∠B=∠C,
∴△AOB∽△DOC,
∴=,
=,
解得AB=100.
答:AB的距离是100米.
9.解:过E作EH⊥CD交CD于H点,交AB于点G,如下图所示:
由已知得,EF⊥FD,AB⊥FD,CD⊥FD,
∵EH⊥CD,EH⊥AB,
∴四边形EFDH为矩形,
∴EF=GB=DH=1.5米,EG=FB=2.5米,GH=BD=8米,
∴AG=AB﹣GB=2.4﹣1.5=0.9米,
∵EH⊥CD,EH⊥AB,
∴AG∥CH,
∴△AEG∽△CEH,
∴=,
∴=,
解得:CH=3.78米,
∴DC=CH+DH=3.78+1.5=5.28米.
答:故树高DC为5.28米.
10.解:(1)如图所示:
(2)如图①所示:使△DEF与△ABC相似的格点F一共有6个.
故答案为:6.
11.解:由题意可得:△DEF∽△DCA,
则=,
∵DE=0.5米,EF=0.25米,DG=1.5m,DC=20m,
∴=,
解得:AC=10,
故AB=AC+BC=10+1.5=11.5(m),
答:旗杆的高度为11.5m.
12.(1)证明:如图,在矩形ABCD中:∠DFC=∠EFB,∠EBF=∠FCD=90°,
∴△BEF∽△CDF;
(2)解:∵由(1)知,△BEF∽△CDF.
∴=,即=,
解得:CF=169.
即:CF的长度是169cm.
13.解:∵AM∥BN,
∴∠A=∠NBC,
∵∠C=∠C,
∴△NBC∽△MAC,
=,
解得NC=m.
14.解:∵OA:OD=OB:OC=3:1,∠COD=∠AOB,
∴△COD∽△BOA.
∴AB:CD=OA:OD=3:1.
∵CD=5cm,
∴AB=15cm.
∴2x+15=16.
∴x=0.5cm.
15.解:根据物体成像原理知:△LMN∽△LBA,
∴.
(1)∵像高MN是35mm,焦距是50mm,拍摄的景物高度AB是4.9m,
∴=,
解得:LD=7,
∴拍摄点距离景物7米;
(2)拍摄高度是2m的景物,拍摄点离景物有4m,像高不变,
∴,
解得:LC=70,
∴相机的焦距应调整为70mm.
16.(1)解:过点C作CE∥BD,交AB于点E,易得四边形CEBD为矩形.
∴CE=BD=3,EB=CD=2,
依题意有 ,即 ,
∴AE=6,
∴AB=AE+EB=6+2=8.
即电线杆AB的高为8米.
(2)不对.理由如下:
设电线杆AB影子全部落在地面上时的影长为x米,则,
∴x=4(米)
答:电线杆AB影子全部落在地面上时的影长为4米.
17.解:∵CD=20m,CE=40m,AD=100m,BE=20m,
∴AC=CD+AD=120m,BC=CE+BE=60m.
∴CE:AC=40:120=1:3,CD:BC=20:60=1:3.
∴CE:AC=CD:BC.
∵∠C=∠C,
∴△CED∽△CAB.
∴DE:AB=CD:BC=1:3.
∴AB=3DE=135m.
∴A、B两地间的距离为135m.
18.解:(1)∵三角形ABC为直角三角形,四边形DEFC是长方形,
∴DE∥CB,
∴,
∵AC、BC分别为60米和120米,CD、CF的长分别为x米和y米,
∴,
即:y=120﹣2x;
(2)S四边形DEFC=xy=x(120﹣2x)=1600,
解得x=20或x=40,
当x=20时,y=120﹣40=80;
当x=40时,y=120﹣80=40;
∴建成的游泳池面积为1600平方米,x=20米,y=80米或x=y=40米.
19.解:过点C作CE∥AD交AB于点E,
则CD=AE=2m,△BCE∽△B′BA′
∴A′B′:B′B=BE:BC
即1.2:2=BE:4
∴BE=2.4
∴AB=2.4+2=4.4
答:这棵树高4.4m.
20.解:因为同一时刻物高与影长成比例,
所以:=,
即:=,
解得落在地上的影长对应的树的高=3m,
所以树的高度为:3+1.2=4.2m.
21.解:根据题意可得:
∠AEB=∠CED,∠BAE=∠DCE=90°,(2分)
∴△ABE∽△CDE,(5分)
∴,(7分)
∴,(8分)
∴AB=13.44(米).(11分)
答:教学大楼的高度AB是13.44米.(12分)
22.解:(1)①∵AB∥EF,
∴△ABM∽△EFM.
∴=,
解得:FM=2;
②同理可得=,
∵AB=CD,
∴==
∴=,
=,
解得:MN=5,
∴影子FM与FN的长的和为定值5;
(2)根据题意设小明由F到B,则影子是从N到C.
由(1)可知=,=,
∵AB=EF,
∴==,
设FN=k,BC=b,
∴QN=3k,QC=3b,
∴FB=2(b﹣k),
NC=3(b﹣k),
设影子的速度为y,
=,
解得y=1.2.
答:影子的速度为1.2米/秒.
23.解:∵∠MAC=∠MOP=90°,
∠AMC=∠OMP,
∴△MAC∽△MOP.
∴,
即,
解得,MA=5米;
同理,由△NBD∽△NOP,可求得NB=1.5米,
∴小明的身影变短了5﹣1.5=3.5米.
24.解:∵CD⊥FB,AB⊥FB,
∴CD∥AB
∴△CGE∽△AHE
∴
即:
∴
∴AH=11.9
∴AB=AH+HB=AH+EF=11.9+1.6=13.5(m).
解答题专题提升训练(附答案)
1.如图,为了估算河的宽度,我们可以在河对岸选定一点A,再在河的这一边选定点B和点C,使得AB⊥BC,然后选定点E,使EC⊥BC,确定BC与AE的交点为D,若测得BD=180m,DC=60m,EC=50m,你能知道小河的宽是多少吗?
2.如图,△ABC是一块锐角三角形余料,边长BC=120cm,高AP=90cm,现在要把它加工成长方形零件DFHE,且满足FH=2DF,F、H在BC上,D、E分别在AB、AC上,求短边DF的长.
3.如图,利用标杆BE测量建筑物的高度,如果标杆BE高1.2m,测得AB=1.6m,BC=12.4m,楼高CD是多少?
4.如图,AB是斜靠在墙壁上的长梯,梯脚B距墙80cm,梯上点D距墙70cm,BD长55cm,求梯子的长.
5.一块材料的形状是锐角三角形ABC,边BC=120mm,高AD=80mm,把它加工成正方形零件如图,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.
(1)求证:△AEF∽△ABC;
(2)求这个正方形零件的边长.
6.如图,直立在点B处的标杆AB长2.5m,站立在点F处的观察者从点E处看到标杆顶A、树顶C在一条直线上.已知BD=10m,FB=3m,人目高EF=1.7m,求树高DC(精确到0.1m)
7.一块直角三角形木板,它的一条直角边AB长1.5m,面积为1.5m2.甲、乙两位木匠分别按图①、②把它加工成一个正方形桌面.请说明哪个正方形面积较大(加工损耗不计).
8.如图,要测量湖岸AB之间的距离,在与湖岸平行的公路上选择两点C、D,确定AD与BC交于点O,测得CD为75m,CO为45m,BO为60m,求湖面AB之间的距离.
9.如图,直立在B处的标杆AB=2.4m,直立在F处的观测者从E处看到标杆顶A、树顶C在同一条直线上(点F,B,D也在同一条直线上).已知BD=8m,FB=2.5m,人高EF=1.5m,求树高CD.
10.图①、图②是6×6的正方形网格,每个小正方形的边长均为1,每个小正方形顶点叫做格点,△ABC的顶点在格点上,点D、E在格点上,连接DE.
(1)在图①、图②中分别找到不同的格点F,使以D、E、F为顶点的三角形与△ABC相似,并画出△DEF(每个网格中只画一个即可).
(2)使△DEF与△ABC相似的格点F一共有 个.
11.如图,某校数学兴趣小组利用自制的直角三角形硬纸板DEF来测量操场旗杆AB的高度,他们通过调整测量位置,使斜边DF与地面保持平行,并使边DE与旗杆顶点A在同一直线上,已知DE=0.5米,EF=0.25米,目测点D到地面的距离DG=1.5米,到旗杆的水平距离DC=20米,求旗杆的高度.
12.如图,矩形ABCD为台球桌面,AD=260cm,AB=130cm,球目前在E点位置,AE=60cm.如果小丁瞄准BC边上的点F将球打过去,经过反弹后,球刚好弹到D点位置.
(1)求证:△BEF∽△CDF;
(2)求CF的长.
13.已知:如图是一束光线射入室内的平面图,上檐边缘射入的光线照在距窗户2.5m处,已知窗户AB高为2m,B点距地面高为1.2m,求下檐光线的落地点N与窗户的距离NC.
如图,零件的外径为16cm,要求它的壁厚x,需要先求出内径AB,现用一个交叉钳(AD与BC相等)去量,若测得OA:OD=OB:OC=3:1,CD=5cm,求零件的壁厚x?
15.如图,是一个照相机成像的示意图.
(1)如果像高MN是35mm,焦距是50mm,拍摄的景物高度AB是4.9m,拍摄点离景物有多远?
(2)如果要完整的拍摄高度是2m的景物,拍摄点离景物有4m,像高不变,则相机的焦距应调整为多少?
16.如图,某一时刻,小明垂直地面竖起一根1m高的直杆,量得其在阳光下的影长为0.5m,此时,旁边一电线杆AB在阳光下的影子分别落在了地上和墙上,他又量得电线杆AB落在地面上的影子部分BD长为3m,落在墙上的影子部分CD高为2m,小明用这些数据很快算出了电线杆AB的高,请你计算一下:
(1)电线杆AB的高为多少?
(2)小亮认为落在地上和墙上的影子长相加就是电线杆影子全部落在地面上时的影长,你认为对吗?若不对,请求出电线杆AB影子全部落在地面上时的影长.
17.如图,点D、E分别在AC、BC上,如果测得CD=20m,CE=40m,AD=100m,BE=20m,DE=45m,求A、B两地间的距离.
18.实验学校有一块直角三角形的空地(如下图的Rt△ABC),它的两直角边AC、BC分别为60米和120米.现准备在AB上选一个点E,在空地中(如图所示)挖掘建造一个矩形游泳池.
(1)设游泳池相邻两边CD、CF的长分别为x米和y米,求y与x之间的函数关系式;
(2)若建成的游泳池面积为1600平方米,求x和y的值.
19.如图所示,在离某建筑物4m处有一棵树,在某时刻,1.2m长的竹竿垂直地面,影长为2m,此时,树的影子有一部分映在地面上,还有一部分影子映在建筑物的墙上,墙上的影高为2m,那么这棵树高约有多少米?
20.教学楼旁边有一棵树,学习了相似三角形后,数学小组的同学想利用树影来测量树高.课外活动时在阳光下他们测得一根长为1m的竹竿的影长是0.9m,但当他们马上测量树高时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上,经过一番争论,小组的同学认为继续测量也可以测出树高,他们测得落在地面的影长2.7m,落在墙壁上的影长1.2m,请你和他们一起算一下,树高为多少?
21.小玲用下面的方法来测量学校教学大楼AB的高度:如图,在水平地面上放一面平面镜,镜子与教学大楼的距离EA=21米.当她与镜子的距离CE=2.5米时,她刚好能从镜子中看到教学大楼的顶端B.已知她的眼睛距地面高度DC=1.6米.请你帮助小玲计算出教学大楼的高度AB是多少米?(注意:根据光的反射定律:反射角等于入射角).
22.夜晚,小明在路灯下散步.若小明身高1.5m,路灯的灯柱高4.5m.
(1)如图1,若小明在相距10米的两路灯AB、CD之间行走(不含两端),他在路灯AB下的影子为FM,在路灯CD下的影子为FN.解答问题:
①若BF=4,求影子FM.②猜想影子FM与FN的长的和为定值吗?说出理由.
(2)有言道:形影不离.其原意为:人的影子与自己紧密相伴,无法分离.但在灯光下,人的速度与影子的速度却不是一样的!如图2,若小明在灯柱PQ前,朝着影子的方向(如图箭头),以0.8米/秒的速度匀速行走,试求他影子的顶端R在地面上移动的速度.
23.如图,路灯(P点)距地面8米,身高1.6米的小明从距路灯的底部(O点)20米的A点,沿OA所在的直线行走14米到B点时,身影的长度是变长了还是变短了?变长或变短了多少米?
24.九年级(1)班课外活动小组利用标杆测量学校旗杆的高度,已知标杆高度CD=3m,标杆与旗杆的水平距离BD=15m,人的眼睛与地面的高度EF=1.6m,人与标杆CD的水平距离DF=2m,求旗杆AB的高度.
参考答案
1.解:由已知得,∠ABD=∠DCE=90°,∠ADB=∠CDE,
∴△ABD∽△ECD,
∴=,
将BD=180m,DC=60m,EC=50m,代入可得:=,
解得:AB=150.
答:小河的宽是150m.
2.解:设DF=xcm,
则DE=2xcm,AK=(90﹣x)cm,
∵DE∥BC,
∴△ADE∽△ABC,
∴=,
∴,
∴x=36,
∴DF的长为36cm.
3.解:∵EB⊥AC,DC⊥AC,
∴EB∥DC,
∴△ABE∽△ACD,
∴=,
∵BE=1.2,AB=1.6,BC=12.4,
∴AC=14,
∴=,
∴CD=10.5.
答:楼高CD是10.5m.
4.解:∵DE⊥AC,BC⊥AC,
∴DE∥BC.
∴△ADE∽△ABC.
∴AD:AB=DE:BC.
∴(AB﹣55):AB=70:80.
∴AB=440cm.
∴梯子长为440cm.
5.(1)证明:∵四边形EFHG是正方形,
∴EF∥BC,
∴△AEF∽△ABC.
(2)解:设这个正方形零件的边长是xmm,
∵EF∥BC,
∴=,
∴=,
解得x=48
答:这个正方形零件的边长是48mm.
6.解:过E作EH⊥CD交CD于H点,交AB于点G,如下图所示:
由已知得,EF⊥FD,AB⊥FD,CD⊥FD,
∵EH⊥CD,EH⊥AB
∴四边形EFDH为矩形
∴EF=GB=DH=1.7,EG=FB=3,GH=BD=10
∴AG=AB﹣GB=0.8
∵EH⊥CD,EH⊥AB,
∴AG∥CH,
∴△AEG∽△CEH
∴
∵EH=EG+GH=13
∴CH=≈3.5
∴CD=CH+HD=5.2
答:故树高DC为5.2米.
7.解:由AB=1.5m,S△ABC=1.5m2,可得BC=2m,
由图①,过点B作Rt△ABC斜边AC上的高,BH交DE于P,交AC于H.
由AB=1.5m,BC=2m,
得AC=(m),
由AC BH=AB BC 可得:BH==1.2(m),
设甲设计的桌面的边长为xm,
∵DE∥AC,
∴Rt△BDE∽Rt△BAC,
∴,即,
解得(m),
由图②,若设乙设计的正方形桌面边长为ym,
由DE∥AB,得Rt△CDE∽Rt△CBA,
∴,即,
解得(m),
∵,,
∴x<y,即x2<y2,
∴S正方形①<S正方形②,
∴第二个正方形面积大.
8.解:∵AB∥CD,
∴∠A=∠D,∠B=∠C,
∴△AOB∽△DOC,
∴=,
=,
解得AB=100.
答:AB的距离是100米.
9.解:过E作EH⊥CD交CD于H点,交AB于点G,如下图所示:
由已知得,EF⊥FD,AB⊥FD,CD⊥FD,
∵EH⊥CD,EH⊥AB,
∴四边形EFDH为矩形,
∴EF=GB=DH=1.5米,EG=FB=2.5米,GH=BD=8米,
∴AG=AB﹣GB=2.4﹣1.5=0.9米,
∵EH⊥CD,EH⊥AB,
∴AG∥CH,
∴△AEG∽△CEH,
∴=,
∴=,
解得:CH=3.78米,
∴DC=CH+DH=3.78+1.5=5.28米.
答:故树高DC为5.28米.
10.解:(1)如图所示:
(2)如图①所示:使△DEF与△ABC相似的格点F一共有6个.
故答案为:6.
11.解:由题意可得:△DEF∽△DCA,
则=,
∵DE=0.5米,EF=0.25米,DG=1.5m,DC=20m,
∴=,
解得:AC=10,
故AB=AC+BC=10+1.5=11.5(m),
答:旗杆的高度为11.5m.
12.(1)证明:如图,在矩形ABCD中:∠DFC=∠EFB,∠EBF=∠FCD=90°,
∴△BEF∽△CDF;
(2)解:∵由(1)知,△BEF∽△CDF.
∴=,即=,
解得:CF=169.
即:CF的长度是169cm.
13.解:∵AM∥BN,
∴∠A=∠NBC,
∵∠C=∠C,
∴△NBC∽△MAC,
=,
解得NC=m.
14.解:∵OA:OD=OB:OC=3:1,∠COD=∠AOB,
∴△COD∽△BOA.
∴AB:CD=OA:OD=3:1.
∵CD=5cm,
∴AB=15cm.
∴2x+15=16.
∴x=0.5cm.
15.解:根据物体成像原理知:△LMN∽△LBA,
∴.
(1)∵像高MN是35mm,焦距是50mm,拍摄的景物高度AB是4.9m,
∴=,
解得:LD=7,
∴拍摄点距离景物7米;
(2)拍摄高度是2m的景物,拍摄点离景物有4m,像高不变,
∴,
解得:LC=70,
∴相机的焦距应调整为70mm.
16.(1)解:过点C作CE∥BD,交AB于点E,易得四边形CEBD为矩形.
∴CE=BD=3,EB=CD=2,
依题意有 ,即 ,
∴AE=6,
∴AB=AE+EB=6+2=8.
即电线杆AB的高为8米.
(2)不对.理由如下:
设电线杆AB影子全部落在地面上时的影长为x米,则,
∴x=4(米)
答:电线杆AB影子全部落在地面上时的影长为4米.
17.解:∵CD=20m,CE=40m,AD=100m,BE=20m,
∴AC=CD+AD=120m,BC=CE+BE=60m.
∴CE:AC=40:120=1:3,CD:BC=20:60=1:3.
∴CE:AC=CD:BC.
∵∠C=∠C,
∴△CED∽△CAB.
∴DE:AB=CD:BC=1:3.
∴AB=3DE=135m.
∴A、B两地间的距离为135m.
18.解:(1)∵三角形ABC为直角三角形,四边形DEFC是长方形,
∴DE∥CB,
∴,
∵AC、BC分别为60米和120米,CD、CF的长分别为x米和y米,
∴,
即:y=120﹣2x;
(2)S四边形DEFC=xy=x(120﹣2x)=1600,
解得x=20或x=40,
当x=20时,y=120﹣40=80;
当x=40时,y=120﹣80=40;
∴建成的游泳池面积为1600平方米,x=20米,y=80米或x=y=40米.
19.解:过点C作CE∥AD交AB于点E,
则CD=AE=2m,△BCE∽△B′BA′
∴A′B′:B′B=BE:BC
即1.2:2=BE:4
∴BE=2.4
∴AB=2.4+2=4.4
答:这棵树高4.4m.
20.解:因为同一时刻物高与影长成比例,
所以:=,
即:=,
解得落在地上的影长对应的树的高=3m,
所以树的高度为:3+1.2=4.2m.
21.解:根据题意可得:
∠AEB=∠CED,∠BAE=∠DCE=90°,(2分)
∴△ABE∽△CDE,(5分)
∴,(7分)
∴,(8分)
∴AB=13.44(米).(11分)
答:教学大楼的高度AB是13.44米.(12分)
22.解:(1)①∵AB∥EF,
∴△ABM∽△EFM.
∴=,
解得:FM=2;
②同理可得=,
∵AB=CD,
∴==
∴=,
=,
解得:MN=5,
∴影子FM与FN的长的和为定值5;
(2)根据题意设小明由F到B,则影子是从N到C.
由(1)可知=,=,
∵AB=EF,
∴==,
设FN=k,BC=b,
∴QN=3k,QC=3b,
∴FB=2(b﹣k),
NC=3(b﹣k),
设影子的速度为y,
=,
解得y=1.2.
答:影子的速度为1.2米/秒.
23.解:∵∠MAC=∠MOP=90°,
∠AMC=∠OMP,
∴△MAC∽△MOP.
∴,
即,
解得,MA=5米;
同理,由△NBD∽△NOP,可求得NB=1.5米,
∴小明的身影变短了5﹣1.5=3.5米.
24.解:∵CD⊥FB,AB⊥FB,
∴CD∥AB
∴△CGE∽△AHE
∴
即:
∴
∴AH=11.9
∴AB=AH+HB=AH+EF=11.9+1.6=13.5(m).
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
