2020-2021学年北京市高三(上)诊断性数学试卷(9月份)人教A版word版含答案
文档属性
| 名称 | 2020-2021学年北京市高三(上)诊断性数学试卷(9月份)人教A版word版含答案 |
|
|
| 格式 | zip | ||
| 文件大小 | 148.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-26 00:00:00 | ||
图片预览



文档简介
2020-2021学年北京市高三(上)诊断性数学试卷(9月份)
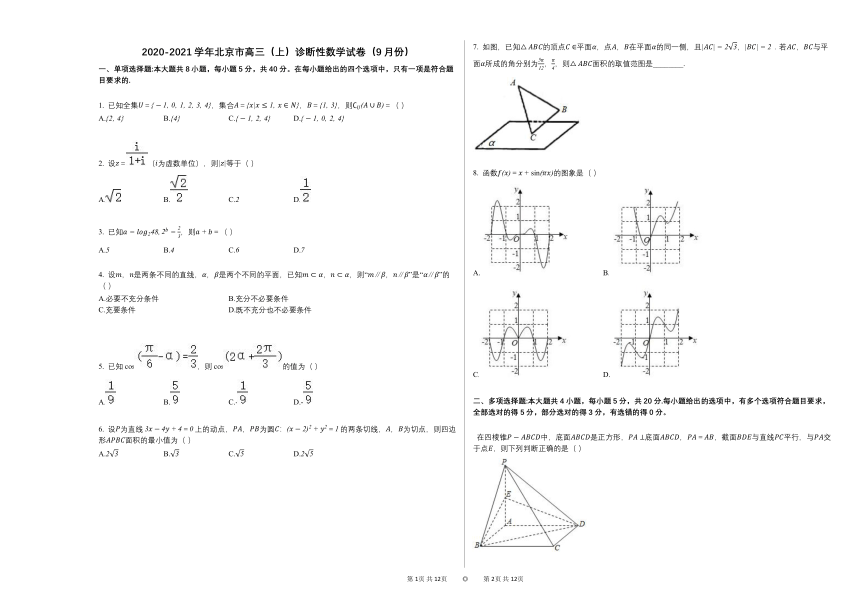
一、单项选择题:本大题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 已知全集=,集合=,=,则=( )
A. B. C. D.
2. 设=(为虚数单位),则等于( )
A. B. C. D.
3. 已知,则=( )
A. B. C. D.
4. 设,是两条不同的直线,,是两个不同的平面,已知,,则“,”是“”的( )
A.必要不充分条件 B.充分不必要条件
C.充要条件 D.既不充分也不必要条件
5. 已知,则的值为( )
A. B. C.- D.-
6. 设为直线=上的动点,,为圆:=的两条切线,,为切点,则四边形面积的最小值为( )
A. B. C. D.
7. 如图,已知的顶点平面,点,在平面的同一侧,且,.若,与平面所成的角分别为,,则面积的取值范图是________.
8. 函数=的图象是( )
A. B.
C. D.
二、多项选择题:本大题共4小题,每小题5分,共20分.每小题给出的选项中,有多个选项符合题目要求,全部选对的得5分,部分选对的得3分,有选错的得0分。
在四棱锥中,底面是正方形,底面,=,截面与直线平行,与交于点,则下列判断正确的是( )
A.与所成的角为
B.为的中点
C.平面
D.三棱锥与四棱锥的体积之比等于
已知双曲线:=的左、右两个焦点分别是、,双曲线的左、右顶点分别为、,点是双曲线上异于、的任意一点,直线=,与双曲线交于、两点,给出下列命题,其中是真命题的有( )
A.直线,斜率之积为
B.双曲线与双曲线有相同渐近线
C.的面积为
D.若,则该双曲线的离心率的取值范围是[]
已知函数=,若有四个不同的实数,,,满足方程===,且,则以下结论一定成立的是( )
A.=
B.=
C.=
D.=
已知数列满足:=,=(,前项和为(参考数据:,),则下列选项正确的是( )
A.
B.是单调递增数列,是单调递减数列
C.
D.
三、填空题:本大题共3小题,每小题5分,共20分.
小红同学去超市买糖果,现有四种不同口味的糖果可供选择(可以有糖果不被选择),单价均为一元一颗,小红只有元钱且要求全部花完,则不同的选购方法共有________种.
已知抛物线=的焦点为,过的直线交抛物线于,两点,若,则点的坐标为________.
已知,,且满足=,则的最小值是________.
四、解答题:本题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤.
在中,,,分别为内角,,的对边,=,=.在下列两个条件中任选一个,求边以及的面积.注:如果选择两个条件分别解答,按第一个解答计分.
条件①=;
条件②=.
已知四棱锥中,底面为矩形,平面平面,===,点,分别是,的中点.
(1)求证:平面;
(2)若与平面所成角的余弦值等于,求的长.
已知数列中,=,且=且.
(1)求数列的通项公式;
(2)设数列的前项和为,求满足的所有正整数的值.
某购物平台为了吸引顾客提升销售额,每年“双十一”购物节都会进行某种商品的促销活动.为了预测年“双十一“购物节中该商品促销活动的参与人数,统计了最近五年的“双十一”购物节参与该商品促销活动的人数(见表);
年份
年份编号
参与人数(百万人)
(1)由收集数据的散点图发现,可用线性回归模型拟合参与人数(百万人)与年份编号之间的相关关系.请用最小二乘法求关于的线性回归方程,并预测年“双十一”购物节参与该商品促销活动的人数;
(2)在年“双十一”购物节前,该购物平台推出订单“秒杀”抢购活动,活动规定每个订单只参加一次“秒杀”抢购,甲、乙、丙三位同学计划在该购物平台分别参加,,三个订单的“秒杀”抢购.若甲、乙、丙参与每个订单的“秒杀”“成功概率均为.记此次活动甲、乙、丙三位同学抢到的订单总数为.
①求的分布列与;
②已知每个订单由件商品组成,记甲、乙、丙三位同学抢购的商品总数量为,若,求取最大值时的正整数的值.
参考公式及数据:①回归方程中斜率和截距的最小二乘法公式分别为:,;
②.
设椭圆:=的离心率=,且过点,).设,是椭圆上的两个不同的动点,且直线,的倾斜角互补.
(1)求证:直线的斜率为定值;
(2)求的面积的最大值.
已知函数=,且在点()处的切线方程为=.
(1)求的解析式;
(2)证明:当时,有成立.
参考答案与试题解析
2020-2021学年北京市高三(上)诊断性数学试卷(9月份)
一、单项选择题:本大题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的.
1.
【答案】
此题暂无答案
【考点】
交常并陆和集工混合运算
【解析】
此题暂无解析
【解答】
此题暂无解答
2.
【答案】
此题暂无答案
【考点】
复根的务
【解析】
此题暂无解析
【解答】
此题暂无解答
3.
【答案】
此题暂无答案
【考点】
对数都北算性质
【解析】
此题暂无解析
【解答】
此题暂无解答
4.
【答案】
此题暂无答案
【考点】
充分常件、头花条件滤充要条件
【解析】
此题暂无解析
【解答】
此题暂无解答
5.
【答案】
此题暂无答案
【考点】
二倍角于三角术数
两角和与射的三题函数
【解析】
此题暂无解析
【解答】
此题暂无解答
6.
【答案】
此题暂无答案
【考点】
圆的水射方程
【解析】
此题暂无解析
【解答】
此题暂无解答
7.
【答案】
此题暂无答案
【考点】
直线与正键所成的角
正因归理
【解析】
此题暂无解析
【解答】
此题暂无解答
8.
【答案】
此题暂无答案
【考点】
函来锰略也与图象的变换
【解析】
此题暂无解析
【解答】
此题暂无解答
二、多项选择题:本大题共4小题,每小题5分,共20分.每小题给出的选项中,有多个选项符合题目要求,全部选对的得5分,部分选对的得3分,有选错的得0分。
【答案】
此题暂无答案
【考点】
棱使、求族非棱台的体积
异面直线表烧所成的角
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
此题暂无答案
【考点】
双曲根气离心率
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
此题暂无答案
【考点】
分段水正的应用
函数根助点与驶还根的关系
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
此题暂无答案
【考点】
数使的种和
【解析】
此题暂无解析
【解答】
此题暂无解答
三、填空题:本大题共3小题,每小题5分,共20分.
【答案】
此题暂无答案
【考点】
排列水使合及原判计数问题
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
此题暂无答案
【考点】
抛物使之性质
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
此题暂无答案
【考点】
直线与都连位置关系
【解析】
此题暂无解析
【解答】
此题暂无解答
四、解答题:本题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤.
【答案】
此题暂无答案
【考点】
余于视理
正因归理
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
此题暂无答案
【考点】
直线与正键所成的角
直线体平硫平行
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
此题暂无答案
【考点】
数于术推式
数使的种和
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
此题暂无答案
【考点】
离散来随机兴苯的期钱与方差
求解线都接归方程
离散验他空变量截其分布列
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
此题暂无答案
【考点】
直线与椭常画位置关系
椭明的钾用
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
此题暂无答案
【考点】
利用三数定究曲纵上迹点切线方程
利验热数技究女数的最值
【解析】
此题暂无解析
【解答】
此题暂无解答
第3页 共16页 ◎ 第4页 共16页
第1页 共16页 ◎ 第2页 共16页
一、单项选择题:本大题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 已知全集=,集合=,=,则=( )
A. B. C. D.
2. 设=(为虚数单位),则等于( )
A. B. C. D.
3. 已知,则=( )
A. B. C. D.
4. 设,是两条不同的直线,,是两个不同的平面,已知,,则“,”是“”的( )
A.必要不充分条件 B.充分不必要条件
C.充要条件 D.既不充分也不必要条件
5. 已知,则的值为( )
A. B. C.- D.-
6. 设为直线=上的动点,,为圆:=的两条切线,,为切点,则四边形面积的最小值为( )
A. B. C. D.
7. 如图,已知的顶点平面,点,在平面的同一侧,且,.若,与平面所成的角分别为,,则面积的取值范图是________.
8. 函数=的图象是( )
A. B.
C. D.
二、多项选择题:本大题共4小题,每小题5分,共20分.每小题给出的选项中,有多个选项符合题目要求,全部选对的得5分,部分选对的得3分,有选错的得0分。
在四棱锥中,底面是正方形,底面,=,截面与直线平行,与交于点,则下列判断正确的是( )
A.与所成的角为
B.为的中点
C.平面
D.三棱锥与四棱锥的体积之比等于
已知双曲线:=的左、右两个焦点分别是、,双曲线的左、右顶点分别为、,点是双曲线上异于、的任意一点,直线=,与双曲线交于、两点,给出下列命题,其中是真命题的有( )
A.直线,斜率之积为
B.双曲线与双曲线有相同渐近线
C.的面积为
D.若,则该双曲线的离心率的取值范围是[]
已知函数=,若有四个不同的实数,,,满足方程===,且,则以下结论一定成立的是( )
A.=
B.=
C.=
D.=
已知数列满足:=,=(,前项和为(参考数据:,),则下列选项正确的是( )
A.
B.是单调递增数列,是单调递减数列
C.
D.
三、填空题:本大题共3小题,每小题5分,共20分.
小红同学去超市买糖果,现有四种不同口味的糖果可供选择(可以有糖果不被选择),单价均为一元一颗,小红只有元钱且要求全部花完,则不同的选购方法共有________种.
已知抛物线=的焦点为,过的直线交抛物线于,两点,若,则点的坐标为________.
已知,,且满足=,则的最小值是________.
四、解答题:本题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤.
在中,,,分别为内角,,的对边,=,=.在下列两个条件中任选一个,求边以及的面积.注:如果选择两个条件分别解答,按第一个解答计分.
条件①=;
条件②=.
已知四棱锥中,底面为矩形,平面平面,===,点,分别是,的中点.
(1)求证:平面;
(2)若与平面所成角的余弦值等于,求的长.
已知数列中,=,且=且.
(1)求数列的通项公式;
(2)设数列的前项和为,求满足的所有正整数的值.
某购物平台为了吸引顾客提升销售额,每年“双十一”购物节都会进行某种商品的促销活动.为了预测年“双十一“购物节中该商品促销活动的参与人数,统计了最近五年的“双十一”购物节参与该商品促销活动的人数(见表);
年份
年份编号
参与人数(百万人)
(1)由收集数据的散点图发现,可用线性回归模型拟合参与人数(百万人)与年份编号之间的相关关系.请用最小二乘法求关于的线性回归方程,并预测年“双十一”购物节参与该商品促销活动的人数;
(2)在年“双十一”购物节前,该购物平台推出订单“秒杀”抢购活动,活动规定每个订单只参加一次“秒杀”抢购,甲、乙、丙三位同学计划在该购物平台分别参加,,三个订单的“秒杀”抢购.若甲、乙、丙参与每个订单的“秒杀”“成功概率均为.记此次活动甲、乙、丙三位同学抢到的订单总数为.
①求的分布列与;
②已知每个订单由件商品组成,记甲、乙、丙三位同学抢购的商品总数量为,若,求取最大值时的正整数的值.
参考公式及数据:①回归方程中斜率和截距的最小二乘法公式分别为:,;
②.
设椭圆:=的离心率=,且过点,).设,是椭圆上的两个不同的动点,且直线,的倾斜角互补.
(1)求证:直线的斜率为定值;
(2)求的面积的最大值.
已知函数=,且在点()处的切线方程为=.
(1)求的解析式;
(2)证明:当时,有成立.
参考答案与试题解析
2020-2021学年北京市高三(上)诊断性数学试卷(9月份)
一、单项选择题:本大题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的.
1.
【答案】
此题暂无答案
【考点】
交常并陆和集工混合运算
【解析】
此题暂无解析
【解答】
此题暂无解答
2.
【答案】
此题暂无答案
【考点】
复根的务
【解析】
此题暂无解析
【解答】
此题暂无解答
3.
【答案】
此题暂无答案
【考点】
对数都北算性质
【解析】
此题暂无解析
【解答】
此题暂无解答
4.
【答案】
此题暂无答案
【考点】
充分常件、头花条件滤充要条件
【解析】
此题暂无解析
【解答】
此题暂无解答
5.
【答案】
此题暂无答案
【考点】
二倍角于三角术数
两角和与射的三题函数
【解析】
此题暂无解析
【解答】
此题暂无解答
6.
【答案】
此题暂无答案
【考点】
圆的水射方程
【解析】
此题暂无解析
【解答】
此题暂无解答
7.
【答案】
此题暂无答案
【考点】
直线与正键所成的角
正因归理
【解析】
此题暂无解析
【解答】
此题暂无解答
8.
【答案】
此题暂无答案
【考点】
函来锰略也与图象的变换
【解析】
此题暂无解析
【解答】
此题暂无解答
二、多项选择题:本大题共4小题,每小题5分,共20分.每小题给出的选项中,有多个选项符合题目要求,全部选对的得5分,部分选对的得3分,有选错的得0分。
【答案】
此题暂无答案
【考点】
棱使、求族非棱台的体积
异面直线表烧所成的角
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
此题暂无答案
【考点】
双曲根气离心率
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
此题暂无答案
【考点】
分段水正的应用
函数根助点与驶还根的关系
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
此题暂无答案
【考点】
数使的种和
【解析】
此题暂无解析
【解答】
此题暂无解答
三、填空题:本大题共3小题,每小题5分,共20分.
【答案】
此题暂无答案
【考点】
排列水使合及原判计数问题
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
此题暂无答案
【考点】
抛物使之性质
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
此题暂无答案
【考点】
直线与都连位置关系
【解析】
此题暂无解析
【解答】
此题暂无解答
四、解答题:本题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤.
【答案】
此题暂无答案
【考点】
余于视理
正因归理
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
此题暂无答案
【考点】
直线与正键所成的角
直线体平硫平行
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
此题暂无答案
【考点】
数于术推式
数使的种和
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
此题暂无答案
【考点】
离散来随机兴苯的期钱与方差
求解线都接归方程
离散验他空变量截其分布列
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
此题暂无答案
【考点】
直线与椭常画位置关系
椭明的钾用
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
此题暂无答案
【考点】
利用三数定究曲纵上迹点切线方程
利验热数技究女数的最值
【解析】
此题暂无解析
【解答】
此题暂无解答
第3页 共16页 ◎ 第4页 共16页
第1页 共16页 ◎ 第2页 共16页
同课章节目录
