【课后培优】13.3.1等腰三角形同步练习(含解析)
文档属性
| 名称 | 【课后培优】13.3.1等腰三角形同步练习(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-27 17:18:05 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
等腰三角形
一、单选题
1.正方形网格中,网格线的交点称为格点.如图,已知A、B是两格点,使得△ABC为等腰三角形的格点C的个数是( )
A.4个 B.5个 C.6个 D.8个
2.等腰三角形的周长为13,其中一边长为3,则该等腰三角形的底边长为( )
A.3 B.5 C.7 D.9
3.如图,CD是等腰三角形ABC底边上的中线,BE平分∠ABC,交CD于点E,AC=8,DE=2,则BCE的面积是( )
A.4 B.6 C.8 D.12
4.如图,在△ABC中,∠ACB=100°,D、E为AB边上的两点,且AC=AE,BC=BD,则∠DCE的度数为( )
A.45° B.40° C.35° D.30°
5.如图,已知△ABC中,AB=AC=24cm,∠B=∠C,BC=16cm,点D为AB的中点,如果点P在线段BC上以4cm/s的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动,当点Q的运动速度为( )cm/s时,能够在某一时刻使△BPD与△CQP全等.
A.4 B.3 C.4或3 D.4或6
6.如图,Rt△ABC中,CF是斜边AB上的高,角平分线BD交CF于G,DE⊥AB于E,则下列结论①∠A=∠BCF,②CD=CG,③AD=BD,④BC=BE中正确的个数是( )
A.1 B.2 C.3 D.4
7.如图,∠A=15°,AB=BC=CD=DE=EF,则∠DEF的度数为( )
A.45° B.60° C.75° D.90°
8.已知:如图,经过线段一端点A有一直线l,直线上l存在点C,使为等腰三角形,这样的点C有( )个.
A.2 B.3 C.4 D.5
9.如图,△ABC中,∠B=40°,AC的垂直平分线交AC于D,交BC于E,且∠EAB:∠CAE=3:1,则∠C等于( )
A.28° B.25° C.22.5° D.20°
10.如图,ABC中,∠A=90°,AC=AB=5,将ABC沿射线AC的方向平移1个单位长度得到DEF,DE与BC交于点G,DC=DG,则阴影部分面积是( )
A.4 B.8 C.9 D.
11.如图,在等腰△ABC中,AB=AC,∠BAC=56°,∠BAC的平分线与AB的中垂线交于点O,点C沿EF折叠后与点O重合,则∠CEF的度数是( )
A.56° B.32° C.50° D.58°
12.如图,将一个等腰直角三角形△ABC按如图方式折叠,若DE=a,DC=b,下列四个结论:①平分∠BDE;②BC长为2a+b;③△是等腰三角形;④△CED的周长等于BC的长.其中,正确的是( )
A.①②④ B.②③④ C.②③ D.②④
二、填空题
13.如图,△ABC中,AB=AC,点D是△ABC内部一点,DB=DC,点E是边AB上一点,若CD平分∠ACE,∠AEC=100°,则∠BDC=_____°.
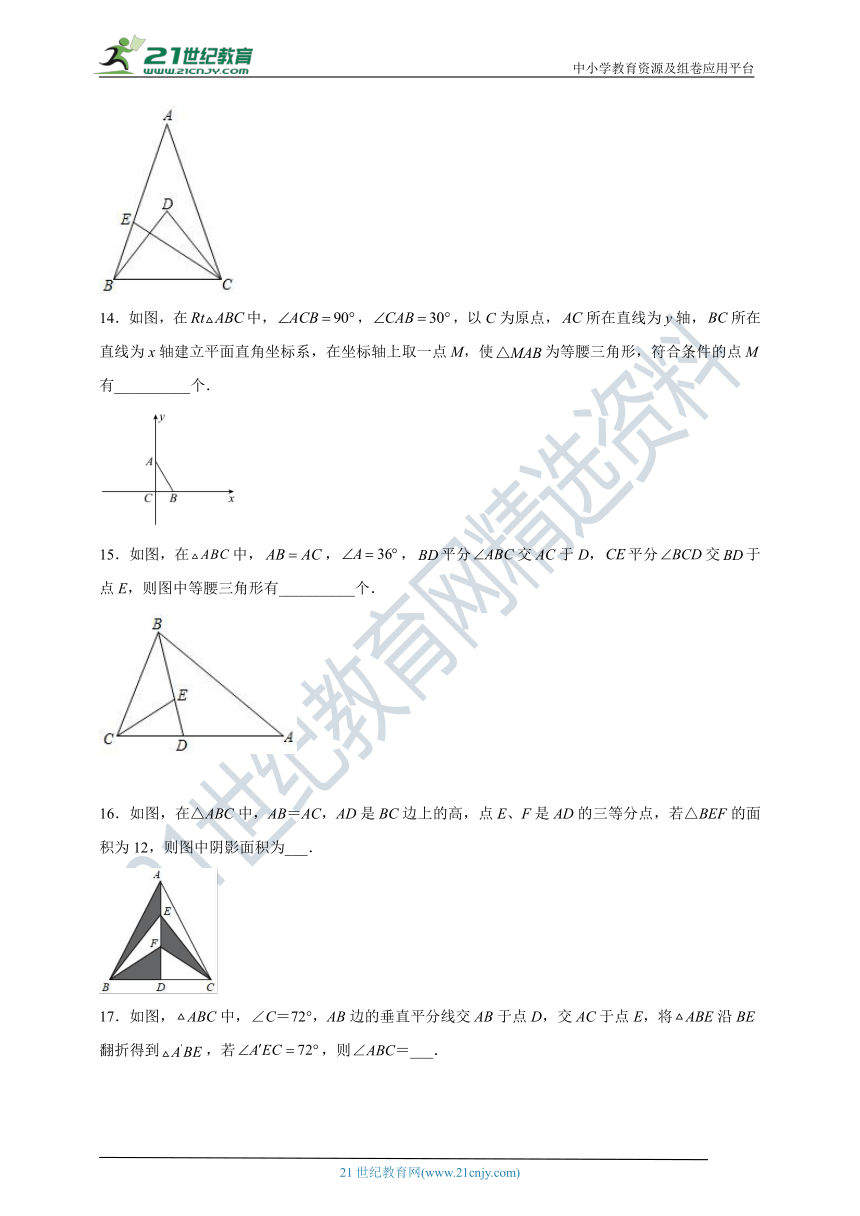
14.如图,在中,,,以C为原点,所在直线为y轴,所在直线为x轴建立平面直角坐标系,在坐标轴上取一点M,使为等腰三角形,符合条件的点M有__________个.
15.如图,在中,,,平分交AC于D,平分交于点E,则图中等腰三角形有__________个.
16.如图,在△ABC中,AB=AC,AD是BC边上的高,点E、F是AD的三等分点,若△BEF的面积为12,则图中阴影面积为___.
17.如图,ABC中,∠C=72°,AB边的垂直平分线交AB于点D,交AC于点E,将ABE沿BE翻折得到,若,则∠ABC=___.
三、解答题
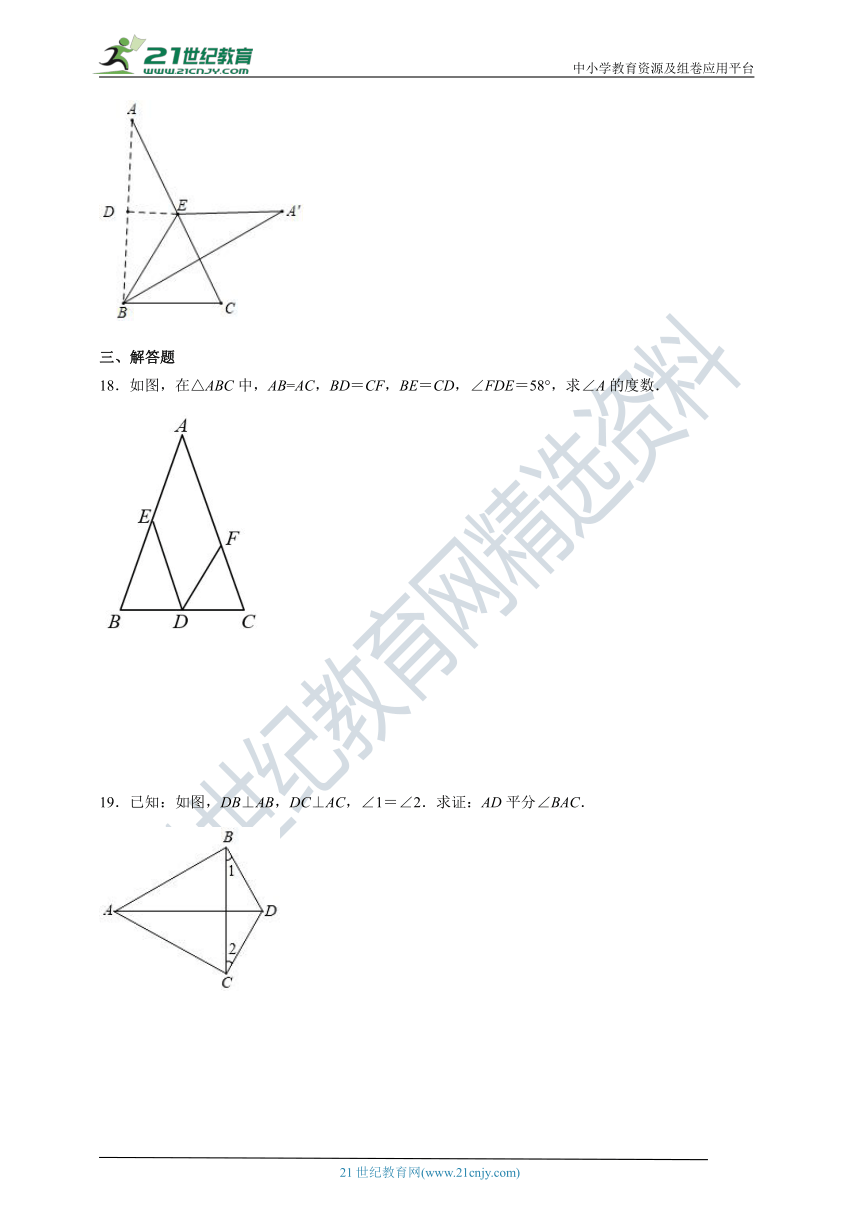
18.如图,在△ABC中,AB=AC,BD=CF,BE=CD,∠FDE=58°,求∠A的度数.
19.已知:如图,DB⊥AB,DC⊥AC,∠1=∠2.求证:AD平分∠BAC.
20.如图,在中,,分别垂直平分边和边,交边于、两点,与相交于点.
(1)若,求的周长.
(2)若,求的度数.
21.如图,在△ABC中,∠BAC = 90°,AB = AC,AD⊥BC于点D,点E在AC边上,连接BE交AD于点F,AG ⊥BE,垂足为点H,交BC于点G.
(1)求证:△FBD≌△AGD;
(2)求证:BD = AF + DG.
22.如图1,为测量池塘宽度,可在池塘外的空地上取任意一点,连接、,并分别延长至点,,使,,连接.
(1)求证:;
(2)如图2,受地形条件的影响,于是采取以下措施:延长至点,使,过点作的平行线,延长至点,连接,测得,,,,请直接写出池塘宽度.
参考答案
1.C
解:由题意可知△ABC为等腰三角形的格点C的情况如图示:
∴满足情况的C点个数为6个;
故选C.
2.A
解:当腰是3时,则另两边是3,7,而3+3<7,不满足三边关系定理,因而应舍去.
当底边是3时,另两边长是5,5,
则该等腰三角形的底边为3,
故选:A.
3.C
解:如图,过点E作于,
,是等腰三角形底边上的中线,
,
平分,,,
,
又,
的面积,
故选:C.
4.B
解:∵在△ABC中,∠ACB=100°,
∴∠A+∠B=80°,即∠B=80°-∠A,
∵AC=AE,BC=BD,
∴∠AEC=∠ACE,∠BDC=∠BCD,
∴在△AEC中,,
在△BDC中,,
∴,
∴在△DEC中,;
故选B.
5.D
解:设经过t秒后,△BPD≌△CQP,
∵AB=AC=24cm,点D为AB的中点,
∴BD=12cm,
∵∠B=∠C,BP=CQ=4t,
∴要使△BPD和△CQP全等,只有BD=CP=12cm,
则16-12=4t,
解得:t=1,
v=4÷1=4cm/秒,
当BP=PC时,△BPD≌△CPQ,
∵BC=16cm,
∴PB=8cm,
t=8÷4=2s,
QC=BD=12cm,
v=12÷2=6cm/秒.
故选:D.
6.C
解:①∵△ABC是直角三角形,
∴∠A+∠ABC=90°,
∵CF⊥AB,
∴∠BCF+∠ABC=90°,
∴∠A=∠BCF,故此小题正确;
②∵BD是∠ABC的平分线,
∴∠DBC=∠DBA,
∵∠BCD=∠CFB=90°,利用互余关系,得∠BGF=∠BDC=∠CGD,
∴CD=CG,故此小题正确;
③由于DE是否是AB的垂直平分线不能确定,故此小题错误;
④∵BD是∠ABC的平分线,DE⊥AB,∠ACB=90°,
∴DE=CD,BD=BD,
∴△BCD≌△BED(HL),
∴BC=BE,故此小题正确.
故①②④正确.
故选:C.
7.B
解:∵AB=BC=CD=DE=EF,∠A=15°,
∴∠BCA=∠A=15°,
∴∠CBD=∠BDC=∠BCA+∠A=15°+15°=30°,
∴,
∴,
∴,
∴,
∴∠DEF=180°﹣(∠EDF+∠EFD)=180°﹣120°=60°.
故选B.
8.C
解:如图所示,以B为圆心,以AB的长为半径画弧与直线l交于点D,此时AB=BD,同理以A为圆心以AB的长为半径与直线l交于E、C,此时AC=AB,AE=AB,再作AB的垂直平分线与直线l交于点F,此时AF=BF,
∴一共有4个点满足题意,
故选C.
9.A
解:设∠CAE=x,则∠EAB=3x.
∵AC的垂直平分线交AC于D,交BC于E,
∴AE=CE.
∴∠C=∠CAE=x.
根据三角形的内角和定理,得
∠C+∠BAC=180°﹣∠B,
即x+4x=140°,
x=28°.
则∠C=28°.
故选:A.
10.D
解:∵∠A=90°,AC=AB=5,
∴S△ABC=×5×5=,
∵CF=1,
∴DC=DG=AC-CF=4,
∴S△DGC=×4×4=8,
由平移的性质得:S△ABC=S△DEF,
∴S阴影=S△DEF-S△DGC=-8=,
故选:D.
11.A
解:如图,连接BO,
∵等腰△ABC中,AB=AC,∠BAC=56°,
∴∠ABC=∠ACB=(180° 56°)÷2=62°,
∵AO是∠BAC的平分线,
∴∠BAO=28°,
又∵OD是AB的中垂线,
∴∠OBA=∠OAB=28°,
∴∠OBC=∠OCB=62° 28°=34°,
∵EF垂直平分线段OC,
∴∠CEF=90° 34°=56°.
故选A.
12.B
解:(1)由折叠的性质得,∠BDC′=22.5°,∠C′DE=∠CDE=45°,
∴DC′不平分∠BDE故①错误;
(2)由折叠性质可得DE=AD=EC=EC′=a,AC=AB=BE=a+b
∴BC=EB+EC=a+b+a=2a+b,故②正确;
(3)∵∠ABC=2∠DBC,
∴∠DBC=22.5°,∠DC′C=∠DCB=45°=∠DBC′+∠BDC′,
∴∠DBC′=∠BDC′=22.5°,
∴BC′=DC′,故③正确;
(4)由折叠的性质可得出△DEC和△DEC'均是等腰直角三角形,
又∵BC′=DC′,
∴△CED的周长=CE+DE+CD=CE+C′E+BC′=BC,故④正确.
综上可得②③④正确,共三个.
故选:B.
13.80
解:设∠ACD=∠DCE=x,∠ECB=y,
∵AB=AC,DB=DC,
∴∠ABC=∠ACB=2x+y,∠DCB=∠DBC=x+y,
∵∠AEC=∠ECB+∠EBC,
∴2x+2y=100°,
∴∠BDC=180°-(∠DCB+∠DBC)=180°-2(x+y)=80°.
故答案为:80.
14.8
解:如图,
①以A为圆心,AB为半径画圆,
交x轴有一点,交y轴有两点,
此时AB = AM,
为等腰三角形;
②以B为圆心,BA为半径画圆,
交直线x轴有两点,交y轴有一点,
此时BM = BA,
为等腰三角形;
③作AB的垂直平分线交y轴于点,交x轴于点,
此时MA = MB,
为等腰三角形,
符合条件的点有8个,
故答案为:8.
15.5
解:AB=AC,
△ABC是等腰三角形,
∠A=36°,
∠ACB=∠ABC=72°,
BD平分∠ABC交AC于D,
∠ABD=∠DBC=36°,
∠A=∠ABD=36°,
△ABD是等腰三角形,
∠BDC=∠A+∠ABD=72°=∠C,
△BDC是等腰三角形,
CE平分∠BCD交BD于点E,
∠BCE=∠DCE=36°,
∠EBC=∠ECB=36°,
△BCE是等腰三角形,
∠DEC=∠EBC+∠ECB=72°=∠EDC,
△CDE是等腰三角形,
共有△ABC 、△ABD 、△BDC 、△BCE 、△CDE 这5个等腰三角形,
故答案为:5.
16.36
解:∵在中,,AD是BC边上的高,
∴,
∵点E、F是AD的三等分点,
∴,
∴,
∴阴影部分的面积为:,
故答案为:36.
17.
解:,
,
,
垂直平分线段,
,
,
由翻折的性质可知,,,
,
,
∵,
,
∵∠C=72°,
,
,
故答案为:.
18.64°
解:∵AB=AC,
∴∠B=∠C,
在△EDB和△DFC中,
∴△EDB≌△DFC(SAS),
∴∠BED=∠CDF,
对于△BED,有∠B+∠BED=∠EDC,
又∵∠EDC=∠FDE+∠CDF,
∴∠B=∠FDE=58°,
∴∠C=∠B=58°,
∴∠A=180°-∠B-∠C=180°-58°-58°=64°.
19.见解析
解:∵DB⊥AB,DC⊥AC
∴∠ABD=∠ACD=90°.
∵∠1=∠2,
∴DB=DC,
∵AD=AD,
∴Rt△ABD≌Rt△ACD.
∴∠BAD=∠CAD,
∴AD平分∠BAC.
20.(1);(2)40°
解:(1)、分别垂直平分和,
,,
的周长;
(2),
,
,,
,
,
,,
,,
.
21.(1)见解析;(2)见解析
解:(1)∵BA=AC,,
∴,
∵,
∴,
∴,
,
∴,
∴AD=BD=DC,
∵,
∴,
∴,
,
∵,
∴
在和中,
∴(ASA)
(2)∵,
∴,
∴,
,
∴,
在和中,
∴(ASA),
∴AF=CG,BF=AG,
∴AF+DG=GC+DG=DC,
∵BD=DC,
∴BD=AF+DG.
22.(1)见详解;(2)21m
解:(1)在△ABO与△CDO中
∵,
∴△ABO≌△CDO(SAS),
∴AB=CD;
(2)如图所示:
延长OF、CE交于点G,
∵∠CEF=140°,∠OFE=110°,
∴∠FEG=40°,∠EFG=70°,
∴∠G=180° 40° 70°=70°,
∴EF=EG,
∵CE=11m,EF=10m,
∴CG=CE+EG=CE+EF=11+10=21m,
∵CG∥AB,
∴∠A=∠C,
在△ABO与△CGO中
,
∴△ABO≌△CGO(ASA)
∴AB=CG=21m.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
等腰三角形
一、单选题
1.正方形网格中,网格线的交点称为格点.如图,已知A、B是两格点,使得△ABC为等腰三角形的格点C的个数是( )
A.4个 B.5个 C.6个 D.8个
2.等腰三角形的周长为13,其中一边长为3,则该等腰三角形的底边长为( )
A.3 B.5 C.7 D.9
3.如图,CD是等腰三角形ABC底边上的中线,BE平分∠ABC,交CD于点E,AC=8,DE=2,则BCE的面积是( )
A.4 B.6 C.8 D.12
4.如图,在△ABC中,∠ACB=100°,D、E为AB边上的两点,且AC=AE,BC=BD,则∠DCE的度数为( )
A.45° B.40° C.35° D.30°
5.如图,已知△ABC中,AB=AC=24cm,∠B=∠C,BC=16cm,点D为AB的中点,如果点P在线段BC上以4cm/s的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动,当点Q的运动速度为( )cm/s时,能够在某一时刻使△BPD与△CQP全等.
A.4 B.3 C.4或3 D.4或6
6.如图,Rt△ABC中,CF是斜边AB上的高,角平分线BD交CF于G,DE⊥AB于E,则下列结论①∠A=∠BCF,②CD=CG,③AD=BD,④BC=BE中正确的个数是( )
A.1 B.2 C.3 D.4
7.如图,∠A=15°,AB=BC=CD=DE=EF,则∠DEF的度数为( )
A.45° B.60° C.75° D.90°
8.已知:如图,经过线段一端点A有一直线l,直线上l存在点C,使为等腰三角形,这样的点C有( )个.
A.2 B.3 C.4 D.5
9.如图,△ABC中,∠B=40°,AC的垂直平分线交AC于D,交BC于E,且∠EAB:∠CAE=3:1,则∠C等于( )
A.28° B.25° C.22.5° D.20°
10.如图,ABC中,∠A=90°,AC=AB=5,将ABC沿射线AC的方向平移1个单位长度得到DEF,DE与BC交于点G,DC=DG,则阴影部分面积是( )
A.4 B.8 C.9 D.
11.如图,在等腰△ABC中,AB=AC,∠BAC=56°,∠BAC的平分线与AB的中垂线交于点O,点C沿EF折叠后与点O重合,则∠CEF的度数是( )
A.56° B.32° C.50° D.58°
12.如图,将一个等腰直角三角形△ABC按如图方式折叠,若DE=a,DC=b,下列四个结论:①平分∠BDE;②BC长为2a+b;③△是等腰三角形;④△CED的周长等于BC的长.其中,正确的是( )
A.①②④ B.②③④ C.②③ D.②④
二、填空题
13.如图,△ABC中,AB=AC,点D是△ABC内部一点,DB=DC,点E是边AB上一点,若CD平分∠ACE,∠AEC=100°,则∠BDC=_____°.
14.如图,在中,,,以C为原点,所在直线为y轴,所在直线为x轴建立平面直角坐标系,在坐标轴上取一点M,使为等腰三角形,符合条件的点M有__________个.
15.如图,在中,,,平分交AC于D,平分交于点E,则图中等腰三角形有__________个.
16.如图,在△ABC中,AB=AC,AD是BC边上的高,点E、F是AD的三等分点,若△BEF的面积为12,则图中阴影面积为___.
17.如图,ABC中,∠C=72°,AB边的垂直平分线交AB于点D,交AC于点E,将ABE沿BE翻折得到,若,则∠ABC=___.
三、解答题
18.如图,在△ABC中,AB=AC,BD=CF,BE=CD,∠FDE=58°,求∠A的度数.
19.已知:如图,DB⊥AB,DC⊥AC,∠1=∠2.求证:AD平分∠BAC.
20.如图,在中,,分别垂直平分边和边,交边于、两点,与相交于点.
(1)若,求的周长.
(2)若,求的度数.
21.如图,在△ABC中,∠BAC = 90°,AB = AC,AD⊥BC于点D,点E在AC边上,连接BE交AD于点F,AG ⊥BE,垂足为点H,交BC于点G.
(1)求证:△FBD≌△AGD;
(2)求证:BD = AF + DG.
22.如图1,为测量池塘宽度,可在池塘外的空地上取任意一点,连接、,并分别延长至点,,使,,连接.
(1)求证:;
(2)如图2,受地形条件的影响,于是采取以下措施:延长至点,使,过点作的平行线,延长至点,连接,测得,,,,请直接写出池塘宽度.
参考答案
1.C
解:由题意可知△ABC为等腰三角形的格点C的情况如图示:
∴满足情况的C点个数为6个;
故选C.
2.A
解:当腰是3时,则另两边是3,7,而3+3<7,不满足三边关系定理,因而应舍去.
当底边是3时,另两边长是5,5,
则该等腰三角形的底边为3,
故选:A.
3.C
解:如图,过点E作于,
,是等腰三角形底边上的中线,
,
平分,,,
,
又,
的面积,
故选:C.
4.B
解:∵在△ABC中,∠ACB=100°,
∴∠A+∠B=80°,即∠B=80°-∠A,
∵AC=AE,BC=BD,
∴∠AEC=∠ACE,∠BDC=∠BCD,
∴在△AEC中,,
在△BDC中,,
∴,
∴在△DEC中,;
故选B.
5.D
解:设经过t秒后,△BPD≌△CQP,
∵AB=AC=24cm,点D为AB的中点,
∴BD=12cm,
∵∠B=∠C,BP=CQ=4t,
∴要使△BPD和△CQP全等,只有BD=CP=12cm,
则16-12=4t,
解得:t=1,
v=4÷1=4cm/秒,
当BP=PC时,△BPD≌△CPQ,
∵BC=16cm,
∴PB=8cm,
t=8÷4=2s,
QC=BD=12cm,
v=12÷2=6cm/秒.
故选:D.
6.C
解:①∵△ABC是直角三角形,
∴∠A+∠ABC=90°,
∵CF⊥AB,
∴∠BCF+∠ABC=90°,
∴∠A=∠BCF,故此小题正确;
②∵BD是∠ABC的平分线,
∴∠DBC=∠DBA,
∵∠BCD=∠CFB=90°,利用互余关系,得∠BGF=∠BDC=∠CGD,
∴CD=CG,故此小题正确;
③由于DE是否是AB的垂直平分线不能确定,故此小题错误;
④∵BD是∠ABC的平分线,DE⊥AB,∠ACB=90°,
∴DE=CD,BD=BD,
∴△BCD≌△BED(HL),
∴BC=BE,故此小题正确.
故①②④正确.
故选:C.
7.B
解:∵AB=BC=CD=DE=EF,∠A=15°,
∴∠BCA=∠A=15°,
∴∠CBD=∠BDC=∠BCA+∠A=15°+15°=30°,
∴,
∴,
∴,
∴,
∴∠DEF=180°﹣(∠EDF+∠EFD)=180°﹣120°=60°.
故选B.
8.C
解:如图所示,以B为圆心,以AB的长为半径画弧与直线l交于点D,此时AB=BD,同理以A为圆心以AB的长为半径与直线l交于E、C,此时AC=AB,AE=AB,再作AB的垂直平分线与直线l交于点F,此时AF=BF,
∴一共有4个点满足题意,
故选C.
9.A
解:设∠CAE=x,则∠EAB=3x.
∵AC的垂直平分线交AC于D,交BC于E,
∴AE=CE.
∴∠C=∠CAE=x.
根据三角形的内角和定理,得
∠C+∠BAC=180°﹣∠B,
即x+4x=140°,
x=28°.
则∠C=28°.
故选:A.
10.D
解:∵∠A=90°,AC=AB=5,
∴S△ABC=×5×5=,
∵CF=1,
∴DC=DG=AC-CF=4,
∴S△DGC=×4×4=8,
由平移的性质得:S△ABC=S△DEF,
∴S阴影=S△DEF-S△DGC=-8=,
故选:D.
11.A
解:如图,连接BO,
∵等腰△ABC中,AB=AC,∠BAC=56°,
∴∠ABC=∠ACB=(180° 56°)÷2=62°,
∵AO是∠BAC的平分线,
∴∠BAO=28°,
又∵OD是AB的中垂线,
∴∠OBA=∠OAB=28°,
∴∠OBC=∠OCB=62° 28°=34°,
∵EF垂直平分线段OC,
∴∠CEF=90° 34°=56°.
故选A.
12.B
解:(1)由折叠的性质得,∠BDC′=22.5°,∠C′DE=∠CDE=45°,
∴DC′不平分∠BDE故①错误;
(2)由折叠性质可得DE=AD=EC=EC′=a,AC=AB=BE=a+b
∴BC=EB+EC=a+b+a=2a+b,故②正确;
(3)∵∠ABC=2∠DBC,
∴∠DBC=22.5°,∠DC′C=∠DCB=45°=∠DBC′+∠BDC′,
∴∠DBC′=∠BDC′=22.5°,
∴BC′=DC′,故③正确;
(4)由折叠的性质可得出△DEC和△DEC'均是等腰直角三角形,
又∵BC′=DC′,
∴△CED的周长=CE+DE+CD=CE+C′E+BC′=BC,故④正确.
综上可得②③④正确,共三个.
故选:B.
13.80
解:设∠ACD=∠DCE=x,∠ECB=y,
∵AB=AC,DB=DC,
∴∠ABC=∠ACB=2x+y,∠DCB=∠DBC=x+y,
∵∠AEC=∠ECB+∠EBC,
∴2x+2y=100°,
∴∠BDC=180°-(∠DCB+∠DBC)=180°-2(x+y)=80°.
故答案为:80.
14.8
解:如图,
①以A为圆心,AB为半径画圆,
交x轴有一点,交y轴有两点,
此时AB = AM,
为等腰三角形;
②以B为圆心,BA为半径画圆,
交直线x轴有两点,交y轴有一点,
此时BM = BA,
为等腰三角形;
③作AB的垂直平分线交y轴于点,交x轴于点,
此时MA = MB,
为等腰三角形,
符合条件的点有8个,
故答案为:8.
15.5
解:AB=AC,
△ABC是等腰三角形,
∠A=36°,
∠ACB=∠ABC=72°,
BD平分∠ABC交AC于D,
∠ABD=∠DBC=36°,
∠A=∠ABD=36°,
△ABD是等腰三角形,
∠BDC=∠A+∠ABD=72°=∠C,
△BDC是等腰三角形,
CE平分∠BCD交BD于点E,
∠BCE=∠DCE=36°,
∠EBC=∠ECB=36°,
△BCE是等腰三角形,
∠DEC=∠EBC+∠ECB=72°=∠EDC,
△CDE是等腰三角形,
共有△ABC 、△ABD 、△BDC 、△BCE 、△CDE 这5个等腰三角形,
故答案为:5.
16.36
解:∵在中,,AD是BC边上的高,
∴,
∵点E、F是AD的三等分点,
∴,
∴,
∴阴影部分的面积为:,
故答案为:36.
17.
解:,
,
,
垂直平分线段,
,
,
由翻折的性质可知,,,
,
,
∵,
,
∵∠C=72°,
,
,
故答案为:.
18.64°
解:∵AB=AC,
∴∠B=∠C,
在△EDB和△DFC中,
∴△EDB≌△DFC(SAS),
∴∠BED=∠CDF,
对于△BED,有∠B+∠BED=∠EDC,
又∵∠EDC=∠FDE+∠CDF,
∴∠B=∠FDE=58°,
∴∠C=∠B=58°,
∴∠A=180°-∠B-∠C=180°-58°-58°=64°.
19.见解析
解:∵DB⊥AB,DC⊥AC
∴∠ABD=∠ACD=90°.
∵∠1=∠2,
∴DB=DC,
∵AD=AD,
∴Rt△ABD≌Rt△ACD.
∴∠BAD=∠CAD,
∴AD平分∠BAC.
20.(1);(2)40°
解:(1)、分别垂直平分和,
,,
的周长;
(2),
,
,,
,
,
,,
,,
.
21.(1)见解析;(2)见解析
解:(1)∵BA=AC,,
∴,
∵,
∴,
∴,
,
∴,
∴AD=BD=DC,
∵,
∴,
∴,
,
∵,
∴
在和中,
∴(ASA)
(2)∵,
∴,
∴,
,
∴,
在和中,
∴(ASA),
∴AF=CG,BF=AG,
∴AF+DG=GC+DG=DC,
∵BD=DC,
∴BD=AF+DG.
22.(1)见详解;(2)21m
解:(1)在△ABO与△CDO中
∵,
∴△ABO≌△CDO(SAS),
∴AB=CD;
(2)如图所示:
延长OF、CE交于点G,
∵∠CEF=140°,∠OFE=110°,
∴∠FEG=40°,∠EFG=70°,
∴∠G=180° 40° 70°=70°,
∴EF=EG,
∵CE=11m,EF=10m,
∴CG=CE+EG=CE+EF=11+10=21m,
∵CG∥AB,
∴∠A=∠C,
在△ABO与△CGO中
,
∴△ABO≌△CGO(ASA)
∴AB=CG=21m.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
