【备考2022】浙江专版数学中考2019-2021年真题分类精编精练(6)坐标系与一次函数(含解析)
文档属性
| 名称 | 【备考2022】浙江专版数学中考2019-2021年真题分类精编精练(6)坐标系与一次函数(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-26 17:12:29 | ||
图片预览




文档简介
【备考2022】浙江专版数学中考2019-2021年真题分类精编精练(6)
坐标系与一次函数(含解析)
学校:___________姓名:___________班级:___________考号:___________
一、选择题(每题3分,共30分)
1.(2019·浙江绍兴·)若三点,,在同一直线上,则的值等于( )
A.-1 B.0 C.3 D.4
2.(2021·浙江嘉兴·)已知点在直线上,且( )
A. B. C. D.
3.(2020·浙江杭州·)在平面直角坐标系中,已知函数y=ax+a(a≠0)的图象过点P(1,2),则该函数的图象可能是( )
A. B.
C. D.
4.(2020·浙江台州·)如图1,小球从左侧的斜坡滚下,到达底端后又沿着右侧斜坡向上滚,在这个过程中,小球的运动速度v(单位:m/s)与运动时间t (单位:s)的函数图象如图2,则该小球的运动路程y(单位:m)与运动时间t(单位:s)之间的函数图象大致是( )
A. B.C. D.
5.(2019·浙江)如图是雷达屏幕在一次探测中发现的多个目标,其中对目标A的位置表述正确的是( )
A.在南偏东75 方向处 B.在5km处
C.在南偏东15 方向5km处 D.在南偏东75 方向5km处
6.(2020·浙江)已知在平面直角坐标系xOy中,直线y=2x+2和直线y=x+2分别交x轴于点A和点B.则下列直线中,与x轴的交点不在线段AB上的直线是( )
A.y=x+2 B.y=x+2 C.y=4x+2 D.y=x+2
7.(2012·浙江温州·)一次函数的图象与y轴的交点坐标是( )
A.(4,0) B.(0,4) C.(2,0) D.(0,2)
8.(2019·浙江嘉兴·)如图,在直角坐标系中,已知菱形OABC的顶点A(1,2),B(3,3).作菱形OABC关于y轴的对称图形OA′B′C′,再作图形OA′B′C′关于点O的中心对称图形OA″B″C″,则点C的对应点C″的坐标是( )
A.(2,-1) B.(1,-2) C. (-2,1) D. (-2,-1)
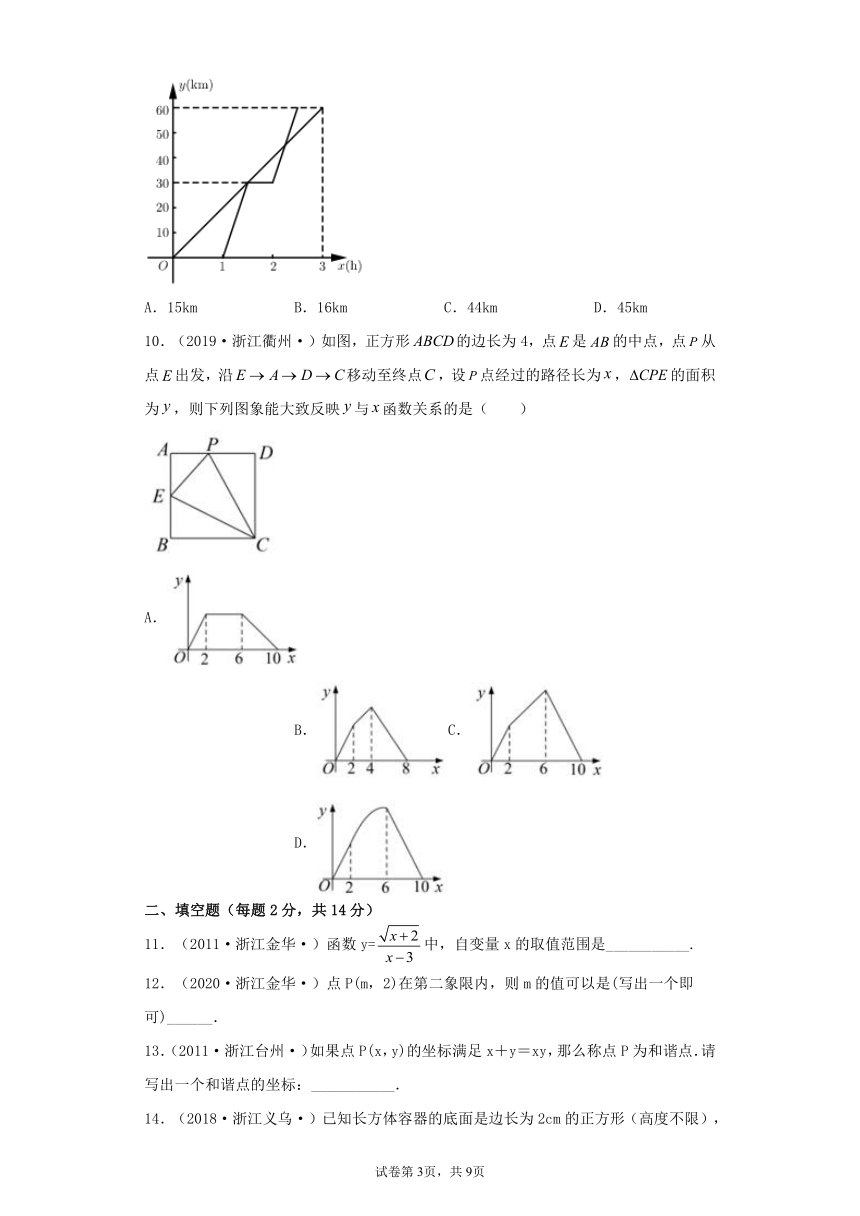
9.(2021·浙江衢州·)已知A,B两地相距60km,甲、乙两人沿同一条公路从A地出发到B地,甲骑自行车匀速行驶3h到达,乙骑摩托车.比甲迟1h出发,行至30km处追上甲,停留半小时后继续以原速行驶.他们离开A地的路程y与甲行驶时间x的函数图象如图所示.当乙再次追上甲时距离B地( )
A.15km B.16km C.44km D.45km
10.(2019·浙江衢州·)如图,正方形的边长为4,点是的中点,点从点出发,沿移动至终点,设点经过的路径长为,的面积为,则下列图象能大致反映与函数关系的是( )
A. B.C. D.
二、填空题(每题2分,共14分)
11.(2011·浙江金华·)函数y=中,自变量x的取值范围是___________.
12.(2020·浙江金华·)点P(m,2)在第二象限内,则m的值可以是(写出一个即可)______.
13.(2011·浙江台州·)如果点P(x,y)的坐标满足x+y=xy,那么称点P为和谐点.请写出一个和谐点的坐标:___________.
14.(2018·浙江义乌·)已知长方体容器的底面是边长为2cm的正方形(高度不限),容器内盛有10cm高的水,现将底面是边长1cm的正方形、高是xcm的长方体铁块竖直放入容器内(铁块全部在水里),容器内的水高y关于x的函数关系式为___________.
15.(2018·浙江衢州·)星期天,小明上午8:00从家里出发,骑车到图书馆去借书,再骑车回到家.他离家的距离y(千米)与时间t(分钟)的关系如图所示,则上午8:45小明离家的距离是__千米.
16.(2019·浙江)元朝朱世杰的《算学启蒙》一书记载:“今有良马日行二百四十里,驽马日行一百五十里,驽马先行一十二日,问良马几何日追及之.”如图是两匹马行走路s关于行走的时间t和函数图象,则两图象交点P的坐标是_____.
17.(2018·浙江台州·)如图,把平面内一条数轴x绕原点O逆时针旋转角θ(0°<θ<90°)得到另一条数轴y,x轴和y轴构成一个平面斜坐标系.规定:过点P作y轴的平行线,交x轴于点A,过点P作x轴的平行线,交y轴于点B,若点A在x轴上对应的实数为a,点B在y轴上对应的实数为b,则称有序实数对(a,b)为点P的斜坐标,在某平面斜坐标系中,已知θ=60°,点M′的斜坐标为(3,2),点N与点M关于y轴对称,则点N的斜坐标为_____.
三、解答题(共56分)
18.(2019·浙江绍兴·)如图是某型号新能源纯电动汽车充满电后,蓄电池剩余电量(千瓦时)关于已行驶路程 (千米)的函数图象.
(1)根据图象,直接写出蓄电池剩余电量为35千瓦时时汽车已行驶的路程,当时,求1千瓦时的电量汽车能行驶的路程;
(2)当时求关于的函数表达式,并计算当汽车已行驶180千米时,蓄电池的剩余电量.
19.(2019·浙江台州·)如图1,某商场在一楼到二楼之间设有上、下行自动扶梯和步行楼梯.甲、乙两人从二楼同时下行,甲乘自动扶梯,乙走步行楼梯,甲离一楼地面的高度(单位:)与下行时间(单位:)之间具有函数关系,乙离一楼地面的高度(单位:)与下行时间(单位:)的函数关系如图2所示.
(1)求关于的函数解析式;
(2)请通过计算说明甲、乙两人谁先到达一楼地面.
20.(2020·浙江绍兴·)我国传统的计重工具﹣﹣秤的应用,方便了人们的生活.如图1,可以用秤砣到秤纽的水平距离,来得出秤钩上所挂物体的重量.称重时,若秤杆上秤砣到秤纽的水平距离为x(厘米)时,秤钩所挂物重为y(斤),则y是x的一次函数.下表中为若干次称重时所记录的一些数据.
x(厘米) 1 2 4 7 11 12
y(斤) 0.75 1.00 1.50 2.75 3.25 3.50
(1)在上表x,y的数据中,发现有一对数据记录错误.在图2中,通过描点的方法,观察判断哪一对是错误的?
(2)根据(1)的发现,问秤杆上秤砣到秤纽的水平距离为16厘米时,秤钩所挂物重是多少?
21.(2020·浙江金华·)某地区山峰的高度每增加1百米,气温大约降低0.6℃.气温T(℃)和高度h(百米)的函数关系如图所示.请根据图象解决下列问题:
(1)求高度为5百米时的气温.
(2)求T关于h的函数表达式.
(3)测得山顶的气温为6℃,求该山峰的高度.
22.(2021·浙江嘉兴·)根据数学家凯勒的“百米赛跑数学模型”,前30米称为“加速期”,30米~80米为“中途期”(m/s)与路程之间的观测数据
(1)是关于的函数吗?为什么?
(2)“加速期”结束时,小斌的速度为多少?
(3)根据如图提供的信息,给小斌提一条训练建议.
23.(2021·浙江绍兴·)I号无人机从海拔10m处出发,以10m/min的速度匀速上升,II号无人机从海拔30m处同时出发,以a(m/min)的速度匀速上升,经过5min两架无人机位于同一海拔高度b(m).无人机海拔高度y(m)与时间x(min)的关系如图.两架无人机都上升了15min.
(1)求b的值及II号无人机海拔高度y(m)与时间x(min)的关系式.
(2)问无人机上升了多少时间,I号无人机比II号无人机高28米.
24.(2021·浙江宁波·)某通讯公司就手机流量套餐推出三种方案,如下表:
A方案 B方案 C方案
每月基本费用(元) 20 56 266
每月免费使用流量(兆) 1024 m 无限
超出后每兆收费(元) n n
A,B,C三种方案每月所需的费用y(元)与每月使用的流量x(兆)之间的函数关系如图所示.
(1)请直接写出m,n的值.
(2)在A方案中,当每月使用的流量不少于1024兆时,求每月所需的费用y(元)与每月使用的流量x(兆)之间的函数关系式.
(3)在这三种方案中,当每月使用的流量超过多少兆时,选择C方案最划算?
25.(2019·浙江宁波·)某风景区内的公路如图1所示,景区内有免费的班车,从入口处出发,沿该公路开往草甸,途中停靠塔林(上下车时间忽略不计).第一班车上午8点发车,以后每隔10分钟有一班车从入口处发车.小聪周末到该风景区游玩,上午7:40到达入口处,因还没到班车发车时间,于是从景区入口处出发,沿该公路步行25分钟后到达塔林.离入口处的路程(米)与时间(分)的函数关系如图2所示.
(1)求第一班车离入口处的路程(米)与时间(分)的函数表达式.
(2)求第一班车从人口处到达塔林所需的时间.
(3)小聪在塔林游玩40分钟后,想坐班车到草甸,则小聪最早能够坐上第几班车?如果他坐这班车到草甸,比他在塔林游玩结束后立即步行到草甸提早了几分钟?(假设每一班车速度均相同,小聪步行速度不变)
26.(2019·浙江湖州·)某校的甲、乙两位老师同住一小区,该小区与学校相距2400米. 甲从小区步行去学校,出发10分钟后乙再出发,乙从小区先骑公共自行车,途经学校义骑行若干米到达还车点后,立即步行走回学校. 已知甲步行的速度比乙步行的速度每分钟快5米. 设甲步行的时间为(分),图1中线段和折线分别表示甲、乙离开小区的路程(米)与甲步行时间(分)的函数关系的图象;图2表示甲、乙两人之间的距离(米)与甲步行时间(分)的函数关系的图象(不完整).根据图1和图2中所给信息,解答下列问题:
(1)求甲步行的速度和乙出发时甲离开小区的路程;
(2)求乙骑自行车的速度和乙到达还车点时甲、乙两人之间的距离;
(3)在图2中,画出当时关于的函数的大致图象. (温馨提示:请画在答题卷相对应的图上)
27.(2021·浙江温州·)某公司生产的一种营养品信息如下表.已知甲食材每千克的进价是乙食材的2倍,用80元购买的甲食材比用20元购买的乙食材多1千克.
营养品信息表
营养成份 每千克含铁42毫克
配料表 原料 每千克含铁
甲食材 50毫克
乙食材 10毫克
规格 每包食材含量 每包单价
A包装 1千克 45元
B包装 0.25千克 12元
(1)问甲、乙两种食材每千克进价分别是多少元?
(2)该公司每日用18000元购进甲、乙两种食材并恰好全部用完.
①问每日购进甲、乙两种食材各多少千克?
②已知每日其他费用为2000元,且生产的营养品当日全部售出.若A的数量不低于B的数量,则A为多少包时,每日所获总利润最大?最大总利润为多少元?
参考答案
1.【分析】利用(1,4),(2,7)两点求出所在的直线解析式,再将点(a,10)代入解析式即可.
解:设经过(1,4),(2,7)两点的直线解析式为y=kx+b,
∴
∴,
∴y=3x+1,
将点(a,10)代入解析式,则a=3;
故选C.
【点评】本题考查一次函数上点的特点;熟练待定系数法求函数解析式是解题的关键.
2.【分析】根据点在直线上,且,先算出的范围,再对不等式变形整理时,需要注意不等号方向的变化.
解:点在直线上,
,
将上式代入中,
得:,
解得:,
由,得:,
(两边同时乘上一个负数,不等号的方向要发生改变),
故选:D.
【点评】本题考查了解一元一次不等式,解题的关键是:要注意在变形的时候,不等号的方向的变化情况.
3.【分析】求得解析式即可判断.
解:∵函数y=ax+a(a≠0)的图象过点P(1,2),
∴2=a+a,解得a=1,
∴y=x+1,
∴直线交y轴的正半轴,且过点(1,2),
故选:A.
【点评】此题考查一次函数表达式及图像的相关知识.
4.【分析】由图2知小球速度先是逐渐增大,后来逐渐减小,则随着时间的增加,小球刚开始路程增加较快,后来增加较慢,由此得出正处答案.
解:由图2知小球速度不断变化,因此判定小球运动速度v与运动时间t之间的函数关系是(为前半程时间,为后半程时间),
∴前半程路程函数表达式为:,后半程路程为,
∵,即前半段图像开口向上,后半段开口向下
∴C项图像满足此关系式,
故答案为:C.
【点评】此题考查根据函数式判断函数图像的大致位置.
5.【分析】根据方向角的定义解答即可.
解:观察图形可得,目标A在南偏东75°方向5km处,
故选D.
【点评】本题考查了方向角的定义,正确理解方向角的意义是解题关键.
6.【分析】分别求出点A、B坐标,再根据各选项解析式求出与x轴交点坐标,判断即可.
解:∵直线y=2x+2和直线y=x+2分别交x轴于点A和点B.
∴A(﹣1,0),B(﹣3,0)
A. y=x+2与x轴的交点为(﹣2,0);故直线y=x+2与x轴的交点在线段AB上;
B. y=x+2与x轴的交点为(﹣,0);故直线y=x+2与x轴的交点在线段AB上;
C. y=4x+2与x轴的交点为(﹣,0);故直线y=4x+2与x轴的交点不在线段AB上;
D. y=x+2与x轴的交点为(﹣,0);故直线y=x+2与x轴的交点在线段AB上;
故选:C
【点评】本题考查了求直线与坐标轴的交点,注意求直线与x轴交点坐标,即把y=0代入函数解析式.
7.【分析】求一次函数图像与y轴的交点坐标,令x=0,求出y值即可.
解:令x=0,
得y=-2×0+4=4,
∴一次函数与y轴的交点坐标是(0,4),
故选B.
【点评】本题考查一次函数与坐标轴的交点坐标问题,求图像与y轴交点坐标时,令x=0,解出y即可;求图像与x轴交点坐标时,令y=0,解出x即可.
8.【分析】先找出对应点,再用线段顺次连接作出图形,根据图形解答即可.
解:如图,
.
故选A.
【点评】本题考查了轴对称作图及中心对称作图,熟练掌握轴对称作图及中心对称的性质是解答本题的关键,中心对称的性质:①关于中心对称的两个图形能够完全重合;②关于中心对称的两个图形,对应点的连线都经过对称中心,并且被对称中心平分.
9.A
【分析】根据图象信息和已知条件,用待定系数法求出,,(),再根据追上时路程相等,求出答案.
解:设,将(3,60)代入表达式,得:
,解得:,
则,
当y=30km时,求得x=,
设,将(1,0),,代入表达式,得:
,得:,
∴,
∴,,
∵乙在途中休息了半小时,到达B地时用半小时,
∴当时,设,将(2,30),代入表达式,得到:
,得:,
∴(),
则当时,,
解得:,
∴,
∴当乙再次追上甲时距离A地45km
所以乙再次追上甲时距离地
故选:A.
【点评】本题主要考查了利用一次函数图像解决实际问题,关键在于理解题意,明白追击问题中追上就是路程相等,再利用待定系数法求出函数表达式,最后进行求解.
10.【分析】结合题意分情况讨论:①当点P在AE上时,②当点P在AD上时,③当点P在DC上时,根据三角形面积公式即可得出每段的y与x的函数表达式.
解:①当点在上时,
∵正方形边长为4,为中点,
∴,
∵点经过的路径长为,
∴,
∴,
②当点在上时,
∵正方形边长为4,为中点,
∴,
∵点经过的路径长为,
∴,,
∴,
,
,
,
③当点在上时,
∵正方形边长为4,为中点,
∴,
∵点经过的路径长为,
∴,,
∴,
综上所述:与的函数表达式为:
.
故答案为C.
【点评】本题考查动点问题的函数图象,解决动点问题的函数图象问题关键是发现y随x的变化而变化的趋势.
11.【分析】根据二次根式的性质和分式的意义,被开方数≥0,分母≠0,可以求出x的范围.
解:根据题意得:x+2≥0且x-3≠0,
解得:x≥-2且x≠3.
【点评】本题考查的知识点为:分式有意义,分母不为0;二次根式的被开方数是非负数.注意二次根式也在分母上时,被开方数应大于0;两个解集,同大取大.
12.【分析】根据第二象限的点符号是“-,+”,m取负数即可.
解:∵点P(m,2)在第二象限内,
∴,
m取负数即可,如m=-1,
故答案为:-1(答案不唯一,负数即可).
【点评】本题考查了已知点所在象限求参数,属于基础题,掌握第二象限点坐标的符号是“-,+”是解题的关键.
13.【分析】由题意点P(x,y)的坐标满足x+y=xy,当x=2时,代入得到2+y=2y,求出y即可.
解:∵点P(x,y)的坐标满足x+y=xy,
当x=2时,代入得:2+y=2y,
∴y=2,
故答案为(2,2).
【点评】本题考查了和谐点的性质及等式求解,比较简单
14.【分析】容器内的水高=容器内原来的水高10cm+放入长方体铁块后增加的水高,依此列式即可.
解:由题意,得y=10+1×1×x÷(2×2)
即y=x+10.
故答案为y=x+10.
【点评】本题考查了根据实际问题列一次函数关系式,正确表示放入长方体铁块后增加的水高是解题的关键.
15.【分析】首先设当40≤t≤60时,距离y(千米)与时间t(分钟)的函数关系为y=kt+b,然后再把(40,2)(60,0)代入可得关于k、b的方程组,解出k、b的值,进而可得函数解析式,再把t=45代入即可.
解:设当40≤t≤60时,距离y(千米)与时间t(分钟)的函数关系为y=kt+b.
∵图象经过(40,2)(60,0),
∴,解得:,
∴y与t的函数关系式为y=﹣,
当t=45时,y=﹣×45+6=1.5.
故答案为1.5.
【点评】本题主要考查了一次函数的应用,关键是正确理解题意,掌握待定系数法求出函数解析式.
16.【分析】根据题意可以得到关于t的方程,从而可以求得点P的坐标,本题得以解决.
解:
由题意可得,150t=240(t﹣12),
解得,t=32,
则150t=150×32=4800,
∴点P的坐标为(32,4800),
故答案为(32,4800).
【点评】本题考查了一次函数的应用,根据题意列出方程150t=240(t﹣12)是解决问题的关键.
17.【分析】如图作ND∥x轴交y轴于D,作NC∥y轴交x轴于C.MN交y轴于K.利用全等三角形的性质,平行四边形的性质求出OC、OD即可;
解:如图作ND∥x轴交y轴于D,作NC∥y轴交x轴于C.MN交y轴于K.
∵NK=MK,∠DNK=∠BMK,∠NKD=∠MKB,
∴△NDK≌△MBK,
∴DN=BM=OC=3,DK=BK,
在Rt△KBM中,BM=3,∠MBK=60°,
∴∠BMK=30°,
∴DK=BK=BM=,
∴OD=5,
∴N(-3,5),
故答案为(-3,5)
【点评】本题考查坐标与图形变化,轴对称等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.
18.【分析】(1)由图象可知,蓄电池剩余电量为35千瓦时时汽车已行驶了150千米,据此即可求出1千瓦时的电量汽车能行驶的路程;
(2)运用待定系数法求出y关于x的函数表达式,再把x=180代入即可求出当汽车已行驶180千米时,蓄电池的剩余电量.
解:(1)由图像可知,蓄电池剩余电量为35千瓦时时汽车行驶了150千米.
1千瓦时可行驶千米.
(2)设,把点,代入,
得,∴,∴.
当时,.
答:当时,函数表达式为,当汽车行驶180千米时,蓄电池剩余电量为20千瓦时.
【点评】本题考查了一次函数的应用,解题的关键:(1)熟练运用待定系数法就解析式;(2)找出剩余油量相同时行驶的距离.本题属于基础题,难度不大,解决该类问题应结合图形,理解图形中点的坐标代表的意义.
19.【分析】(1)设关于的函数解析式是,把(0,6)(15,3)代入即可求解;(2)分别求出当时,当时x的值即可比较.
解:(1)设关于的函数解析式是,
,解得,,
即关于的函数解析式是;
(2)当时,,得,
当时,,得,
∵,
∴甲先到达地面.
【点评】此题主要考查一次函数的应用,解题的关键是根据题意求出一次函数解析式进行求解.
20.【分析】(1)利用描点法画出图形即可判断.
(2)设函数关系式为y=kx+b,利用待定系数法解决问题即可.
解:(1)观察图象可知:x=7,y=2.75这组数据错误.
(2)设y=kx+b,把x=1,y=0.75,x=2,y=1代入可得,
解得,
∴,
当x=16时,y=4.5,
答:秤杆上秤砣到秤纽的水平距离为16厘米时,秤钩所挂物重是4.5斤.
【点评】此题考查画一次函数的图象的方法,待定系数法求一次函数的解析式,一次函数的实际应用,正确计算是解此题的关键.
21.【分析】(1)根据高度每增加1百米,气温大约降低0.6℃,由3百米时温度为13.2°C,即可得出高度为5百米时的气温;
(2)应用待定系数法解答即可;
(3)根据(2)T=-0.6h+15的结论,将T=6代入,解答即可.
解:(1)由题意得 高度增加2百米,则温度降低2×0.6=1.2(℃).
∴13.2-1.2=12
∴高度为5百米时的气温大约是12℃.
(2)设T=-0.6h+b(k≠0),
当h=3时,T=13.2,
13.2=-0.63+b,
解得 b=15.
∴T=-0.6h+15.
(3)当T=6时,6=-0.6h+15,
解得h=15.
∴该山峰的高度大约为15百米.
【点评】本题考查一次函数的应用,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答问题.
22.【分析】(1)根据函数的概念进行解答;
(2)通过识图读取相关信息;
(3)根据图像信息进行解答.
解:(1)是的函数.
在这个变化过程中,对于的每一个确定的值,都有唯一确定的值与之对应.
(2)“加速期”结束时,小斌的速度为10.4m/s.
(3)答案不唯一.例如:根据图象信息,小斌在80米左右时速度下降明显,建议增加耐力训练,提高成绩.
【点评】本题考查通过函数图像读取信息,理解函数的概念,准确识图是解题关键.
23.【分析】(1)直接利用I号无人机从海拔10m处出发,以10m/min的速度匀速上升,求出其5分钟后的高度即可;
(2)将I号无人机的高度表达式减去II号无人机高度表达式,令其值为28,求解即可.
解:(1).
设,
将,代入得:
,
∴;
.
(2)令,
解得,满足题意;
无人机上升12min,I号无人机比II号无人机高28米.
【点评】本题考查了一次函数的实际应用,涉及到了求一次函数的表达式,两个一次函数值之间的比较等内容,解决本题的关键是读懂题意,与图形建立关联,能建立高度的表达式等,本题着重于对函数概念的理解与应用,考查了学生的基本功.
24.【分析】(1)m的值可以从图象上直接读取,n的值可以根据方案A和方案B的费用差和流量差相除求得;
(2)直接运用待定系数法求解即可;
(3)计算出方案C的图象与方案B的图象的交点表示的数值即可求解.
解:(1)
.
(2)设函数表达式为,
把,代入,得
,
解得,
∴y关于x的函数表达式.
(注:x的取值范围对考生不作要求)
(3)(兆).
由图象得,当每月使用的流量超过3772兆时,选择C方案最划算.
【点评】本题考查一次函数的应用,解答本题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.
25.【分析】(1)设y=kx+b,运用待定系数法求解即可;
(2)把y=1500代入(1)的结论即可;
(3)设小聪坐上了第n班车,30-25+10(n-1)≥40,解得n≥4.5,可得小聪坐上了第5班车,再根据“路程、速度与时间的关系”解答即可.
(1)解:由题意得,可设函数表达式为:.
把,代入,得,
解得.
∴第一班车离入口处的路程(米)与时间(分)的函数表达式为.
(2)解:把代入,解得,
(分).
∴第一班车到塔林所需时间10分钟.
(3)解:设小聪坐上第班车.
,解得,
∴小聪最早坐上第5班车.
等班车时间为5分钟,
坐班车所需时间:(分),
∴步行所需时间:(分),
(分).
∴小聪坐班车去草甸比他游玩结束后立即步行到达草甸提早7分钟
【点评】本题主要考查了一次函数的应用,熟练掌握待定系数法求出函数解析式是解答本题的关键.
26.【分析】(1)根据函数图象中的数据可以求得甲步行的速度和乙出发时甲离开小区的路程;
(2)根据函数图象中的数据可以求得OA的函数解析式,然后将x=18代入OA的函数解析式,即可求得点E的纵坐标,进而可以求得乙骑自行车的速度和乙到达还车点时甲、乙两人之间的距离;
(3)根据题意可以求得乙到达学校的时间,从而可以函数图象补充完整.
解:(1)由题意,得:甲步行的速度是 (米/分),
∴乙出发时甲离开小区的路程是 (米).
(2)设直线的解析式为:,
∵直线过点,
∴,
解得,
∴直线的解析式为:.
∴当时,,
∴乙骑自行车的速度是 (米/分).
∵乙骑自行车的时间为 (分),
∴乙骑自行车的路程为 (米).
当时,甲走过的路程是 (米),
∴乙到达还车点时,甲、乙两人之间的距离是 (米).
(3)乙步行的速度为:80-5=75(米/分),
乙到达学校用的时间为:25+(2700-2400)÷75=29(分),
当25≤x≤30时s关于x的函数的大致图象如图所示.
【点评】本题考查一次函数的应用,解答本题的关键是明确题意,利用一次函数的性质和数形结合的思想解答.
27.【分析】(1)设乙食材每千克进价为元,根据用80元购买的甲食材比用20元购买的乙食材多1千克列分式方程即可求解;
(2)①设每日购进甲食材千克,乙食材千克.根据每日用18000元购进甲、乙两种食材并恰好全部用完,利用进货总金额为180000元,含铁量一定列出二元一次方程组即可求解;
②设为包,根据题意,可以得到每日所获总利润与m的函数关系式,再根据A的数量不低于B的数量,可以得到m的取值范围,从而可以求得总利润的最大值.
解:(1)设乙食材每千克进价为元,则甲食材每千克进价为元,
由题意得,解得.
经检验,是所列方程的根,且符合题意.
(元).
答:甲、乙两种食材每千克进价分别为40元、20元.
(2)①设每日购进甲食材千克,乙食材千克.
由题意得,解得
答:每日购进甲食材400千克,乙食材100千克.
②设为包,则为包.
记总利润为元,则
.
的数量不低于的数量,
,.
,随的增大而减小。
当时,的最大值为2800元.
答:当为400包时,总利润最大.最大总利润为2800元.
【点评】本题主要考查了一次函数的应用、分式方程、二元一次方程的应用,解答本题时要明确题意、弄清表格数据的意义及各种量之间关系,利用方程的求未知量和一次函数的性质解答,注意分式方程要检验.
试卷第8页,共9页
试卷第1页,共9页
坐标系与一次函数(含解析)
学校:___________姓名:___________班级:___________考号:___________
一、选择题(每题3分,共30分)
1.(2019·浙江绍兴·)若三点,,在同一直线上,则的值等于( )
A.-1 B.0 C.3 D.4
2.(2021·浙江嘉兴·)已知点在直线上,且( )
A. B. C. D.
3.(2020·浙江杭州·)在平面直角坐标系中,已知函数y=ax+a(a≠0)的图象过点P(1,2),则该函数的图象可能是( )
A. B.
C. D.
4.(2020·浙江台州·)如图1,小球从左侧的斜坡滚下,到达底端后又沿着右侧斜坡向上滚,在这个过程中,小球的运动速度v(单位:m/s)与运动时间t (单位:s)的函数图象如图2,则该小球的运动路程y(单位:m)与运动时间t(单位:s)之间的函数图象大致是( )
A. B.C. D.
5.(2019·浙江)如图是雷达屏幕在一次探测中发现的多个目标,其中对目标A的位置表述正确的是( )
A.在南偏东75 方向处 B.在5km处
C.在南偏东15 方向5km处 D.在南偏东75 方向5km处
6.(2020·浙江)已知在平面直角坐标系xOy中,直线y=2x+2和直线y=x+2分别交x轴于点A和点B.则下列直线中,与x轴的交点不在线段AB上的直线是( )
A.y=x+2 B.y=x+2 C.y=4x+2 D.y=x+2
7.(2012·浙江温州·)一次函数的图象与y轴的交点坐标是( )
A.(4,0) B.(0,4) C.(2,0) D.(0,2)
8.(2019·浙江嘉兴·)如图,在直角坐标系中,已知菱形OABC的顶点A(1,2),B(3,3).作菱形OABC关于y轴的对称图形OA′B′C′,再作图形OA′B′C′关于点O的中心对称图形OA″B″C″,则点C的对应点C″的坐标是( )
A.(2,-1) B.(1,-2) C. (-2,1) D. (-2,-1)
9.(2021·浙江衢州·)已知A,B两地相距60km,甲、乙两人沿同一条公路从A地出发到B地,甲骑自行车匀速行驶3h到达,乙骑摩托车.比甲迟1h出发,行至30km处追上甲,停留半小时后继续以原速行驶.他们离开A地的路程y与甲行驶时间x的函数图象如图所示.当乙再次追上甲时距离B地( )
A.15km B.16km C.44km D.45km
10.(2019·浙江衢州·)如图,正方形的边长为4,点是的中点,点从点出发,沿移动至终点,设点经过的路径长为,的面积为,则下列图象能大致反映与函数关系的是( )
A. B.C. D.
二、填空题(每题2分,共14分)
11.(2011·浙江金华·)函数y=中,自变量x的取值范围是___________.
12.(2020·浙江金华·)点P(m,2)在第二象限内,则m的值可以是(写出一个即可)______.
13.(2011·浙江台州·)如果点P(x,y)的坐标满足x+y=xy,那么称点P为和谐点.请写出一个和谐点的坐标:___________.
14.(2018·浙江义乌·)已知长方体容器的底面是边长为2cm的正方形(高度不限),容器内盛有10cm高的水,现将底面是边长1cm的正方形、高是xcm的长方体铁块竖直放入容器内(铁块全部在水里),容器内的水高y关于x的函数关系式为___________.
15.(2018·浙江衢州·)星期天,小明上午8:00从家里出发,骑车到图书馆去借书,再骑车回到家.他离家的距离y(千米)与时间t(分钟)的关系如图所示,则上午8:45小明离家的距离是__千米.
16.(2019·浙江)元朝朱世杰的《算学启蒙》一书记载:“今有良马日行二百四十里,驽马日行一百五十里,驽马先行一十二日,问良马几何日追及之.”如图是两匹马行走路s关于行走的时间t和函数图象,则两图象交点P的坐标是_____.
17.(2018·浙江台州·)如图,把平面内一条数轴x绕原点O逆时针旋转角θ(0°<θ<90°)得到另一条数轴y,x轴和y轴构成一个平面斜坐标系.规定:过点P作y轴的平行线,交x轴于点A,过点P作x轴的平行线,交y轴于点B,若点A在x轴上对应的实数为a,点B在y轴上对应的实数为b,则称有序实数对(a,b)为点P的斜坐标,在某平面斜坐标系中,已知θ=60°,点M′的斜坐标为(3,2),点N与点M关于y轴对称,则点N的斜坐标为_____.
三、解答题(共56分)
18.(2019·浙江绍兴·)如图是某型号新能源纯电动汽车充满电后,蓄电池剩余电量(千瓦时)关于已行驶路程 (千米)的函数图象.
(1)根据图象,直接写出蓄电池剩余电量为35千瓦时时汽车已行驶的路程,当时,求1千瓦时的电量汽车能行驶的路程;
(2)当时求关于的函数表达式,并计算当汽车已行驶180千米时,蓄电池的剩余电量.
19.(2019·浙江台州·)如图1,某商场在一楼到二楼之间设有上、下行自动扶梯和步行楼梯.甲、乙两人从二楼同时下行,甲乘自动扶梯,乙走步行楼梯,甲离一楼地面的高度(单位:)与下行时间(单位:)之间具有函数关系,乙离一楼地面的高度(单位:)与下行时间(单位:)的函数关系如图2所示.
(1)求关于的函数解析式;
(2)请通过计算说明甲、乙两人谁先到达一楼地面.
20.(2020·浙江绍兴·)我国传统的计重工具﹣﹣秤的应用,方便了人们的生活.如图1,可以用秤砣到秤纽的水平距离,来得出秤钩上所挂物体的重量.称重时,若秤杆上秤砣到秤纽的水平距离为x(厘米)时,秤钩所挂物重为y(斤),则y是x的一次函数.下表中为若干次称重时所记录的一些数据.
x(厘米) 1 2 4 7 11 12
y(斤) 0.75 1.00 1.50 2.75 3.25 3.50
(1)在上表x,y的数据中,发现有一对数据记录错误.在图2中,通过描点的方法,观察判断哪一对是错误的?
(2)根据(1)的发现,问秤杆上秤砣到秤纽的水平距离为16厘米时,秤钩所挂物重是多少?
21.(2020·浙江金华·)某地区山峰的高度每增加1百米,气温大约降低0.6℃.气温T(℃)和高度h(百米)的函数关系如图所示.请根据图象解决下列问题:
(1)求高度为5百米时的气温.
(2)求T关于h的函数表达式.
(3)测得山顶的气温为6℃,求该山峰的高度.
22.(2021·浙江嘉兴·)根据数学家凯勒的“百米赛跑数学模型”,前30米称为“加速期”,30米~80米为“中途期”(m/s)与路程之间的观测数据
(1)是关于的函数吗?为什么?
(2)“加速期”结束时,小斌的速度为多少?
(3)根据如图提供的信息,给小斌提一条训练建议.
23.(2021·浙江绍兴·)I号无人机从海拔10m处出发,以10m/min的速度匀速上升,II号无人机从海拔30m处同时出发,以a(m/min)的速度匀速上升,经过5min两架无人机位于同一海拔高度b(m).无人机海拔高度y(m)与时间x(min)的关系如图.两架无人机都上升了15min.
(1)求b的值及II号无人机海拔高度y(m)与时间x(min)的关系式.
(2)问无人机上升了多少时间,I号无人机比II号无人机高28米.
24.(2021·浙江宁波·)某通讯公司就手机流量套餐推出三种方案,如下表:
A方案 B方案 C方案
每月基本费用(元) 20 56 266
每月免费使用流量(兆) 1024 m 无限
超出后每兆收费(元) n n
A,B,C三种方案每月所需的费用y(元)与每月使用的流量x(兆)之间的函数关系如图所示.
(1)请直接写出m,n的值.
(2)在A方案中,当每月使用的流量不少于1024兆时,求每月所需的费用y(元)与每月使用的流量x(兆)之间的函数关系式.
(3)在这三种方案中,当每月使用的流量超过多少兆时,选择C方案最划算?
25.(2019·浙江宁波·)某风景区内的公路如图1所示,景区内有免费的班车,从入口处出发,沿该公路开往草甸,途中停靠塔林(上下车时间忽略不计).第一班车上午8点发车,以后每隔10分钟有一班车从入口处发车.小聪周末到该风景区游玩,上午7:40到达入口处,因还没到班车发车时间,于是从景区入口处出发,沿该公路步行25分钟后到达塔林.离入口处的路程(米)与时间(分)的函数关系如图2所示.
(1)求第一班车离入口处的路程(米)与时间(分)的函数表达式.
(2)求第一班车从人口处到达塔林所需的时间.
(3)小聪在塔林游玩40分钟后,想坐班车到草甸,则小聪最早能够坐上第几班车?如果他坐这班车到草甸,比他在塔林游玩结束后立即步行到草甸提早了几分钟?(假设每一班车速度均相同,小聪步行速度不变)
26.(2019·浙江湖州·)某校的甲、乙两位老师同住一小区,该小区与学校相距2400米. 甲从小区步行去学校,出发10分钟后乙再出发,乙从小区先骑公共自行车,途经学校义骑行若干米到达还车点后,立即步行走回学校. 已知甲步行的速度比乙步行的速度每分钟快5米. 设甲步行的时间为(分),图1中线段和折线分别表示甲、乙离开小区的路程(米)与甲步行时间(分)的函数关系的图象;图2表示甲、乙两人之间的距离(米)与甲步行时间(分)的函数关系的图象(不完整).根据图1和图2中所给信息,解答下列问题:
(1)求甲步行的速度和乙出发时甲离开小区的路程;
(2)求乙骑自行车的速度和乙到达还车点时甲、乙两人之间的距离;
(3)在图2中,画出当时关于的函数的大致图象. (温馨提示:请画在答题卷相对应的图上)
27.(2021·浙江温州·)某公司生产的一种营养品信息如下表.已知甲食材每千克的进价是乙食材的2倍,用80元购买的甲食材比用20元购买的乙食材多1千克.
营养品信息表
营养成份 每千克含铁42毫克
配料表 原料 每千克含铁
甲食材 50毫克
乙食材 10毫克
规格 每包食材含量 每包单价
A包装 1千克 45元
B包装 0.25千克 12元
(1)问甲、乙两种食材每千克进价分别是多少元?
(2)该公司每日用18000元购进甲、乙两种食材并恰好全部用完.
①问每日购进甲、乙两种食材各多少千克?
②已知每日其他费用为2000元,且生产的营养品当日全部售出.若A的数量不低于B的数量,则A为多少包时,每日所获总利润最大?最大总利润为多少元?
参考答案
1.【分析】利用(1,4),(2,7)两点求出所在的直线解析式,再将点(a,10)代入解析式即可.
解:设经过(1,4),(2,7)两点的直线解析式为y=kx+b,
∴
∴,
∴y=3x+1,
将点(a,10)代入解析式,则a=3;
故选C.
【点评】本题考查一次函数上点的特点;熟练待定系数法求函数解析式是解题的关键.
2.【分析】根据点在直线上,且,先算出的范围,再对不等式变形整理时,需要注意不等号方向的变化.
解:点在直线上,
,
将上式代入中,
得:,
解得:,
由,得:,
(两边同时乘上一个负数,不等号的方向要发生改变),
故选:D.
【点评】本题考查了解一元一次不等式,解题的关键是:要注意在变形的时候,不等号的方向的变化情况.
3.【分析】求得解析式即可判断.
解:∵函数y=ax+a(a≠0)的图象过点P(1,2),
∴2=a+a,解得a=1,
∴y=x+1,
∴直线交y轴的正半轴,且过点(1,2),
故选:A.
【点评】此题考查一次函数表达式及图像的相关知识.
4.【分析】由图2知小球速度先是逐渐增大,后来逐渐减小,则随着时间的增加,小球刚开始路程增加较快,后来增加较慢,由此得出正处答案.
解:由图2知小球速度不断变化,因此判定小球运动速度v与运动时间t之间的函数关系是(为前半程时间,为后半程时间),
∴前半程路程函数表达式为:,后半程路程为,
∵,即前半段图像开口向上,后半段开口向下
∴C项图像满足此关系式,
故答案为:C.
【点评】此题考查根据函数式判断函数图像的大致位置.
5.【分析】根据方向角的定义解答即可.
解:观察图形可得,目标A在南偏东75°方向5km处,
故选D.
【点评】本题考查了方向角的定义,正确理解方向角的意义是解题关键.
6.【分析】分别求出点A、B坐标,再根据各选项解析式求出与x轴交点坐标,判断即可.
解:∵直线y=2x+2和直线y=x+2分别交x轴于点A和点B.
∴A(﹣1,0),B(﹣3,0)
A. y=x+2与x轴的交点为(﹣2,0);故直线y=x+2与x轴的交点在线段AB上;
B. y=x+2与x轴的交点为(﹣,0);故直线y=x+2与x轴的交点在线段AB上;
C. y=4x+2与x轴的交点为(﹣,0);故直线y=4x+2与x轴的交点不在线段AB上;
D. y=x+2与x轴的交点为(﹣,0);故直线y=x+2与x轴的交点在线段AB上;
故选:C
【点评】本题考查了求直线与坐标轴的交点,注意求直线与x轴交点坐标,即把y=0代入函数解析式.
7.【分析】求一次函数图像与y轴的交点坐标,令x=0,求出y值即可.
解:令x=0,
得y=-2×0+4=4,
∴一次函数与y轴的交点坐标是(0,4),
故选B.
【点评】本题考查一次函数与坐标轴的交点坐标问题,求图像与y轴交点坐标时,令x=0,解出y即可;求图像与x轴交点坐标时,令y=0,解出x即可.
8.【分析】先找出对应点,再用线段顺次连接作出图形,根据图形解答即可.
解:如图,
.
故选A.
【点评】本题考查了轴对称作图及中心对称作图,熟练掌握轴对称作图及中心对称的性质是解答本题的关键,中心对称的性质:①关于中心对称的两个图形能够完全重合;②关于中心对称的两个图形,对应点的连线都经过对称中心,并且被对称中心平分.
9.A
【分析】根据图象信息和已知条件,用待定系数法求出,,(),再根据追上时路程相等,求出答案.
解:设,将(3,60)代入表达式,得:
,解得:,
则,
当y=30km时,求得x=,
设,将(1,0),,代入表达式,得:
,得:,
∴,
∴,,
∵乙在途中休息了半小时,到达B地时用半小时,
∴当时,设,将(2,30),代入表达式,得到:
,得:,
∴(),
则当时,,
解得:,
∴,
∴当乙再次追上甲时距离A地45km
所以乙再次追上甲时距离地
故选:A.
【点评】本题主要考查了利用一次函数图像解决实际问题,关键在于理解题意,明白追击问题中追上就是路程相等,再利用待定系数法求出函数表达式,最后进行求解.
10.【分析】结合题意分情况讨论:①当点P在AE上时,②当点P在AD上时,③当点P在DC上时,根据三角形面积公式即可得出每段的y与x的函数表达式.
解:①当点在上时,
∵正方形边长为4,为中点,
∴,
∵点经过的路径长为,
∴,
∴,
②当点在上时,
∵正方形边长为4,为中点,
∴,
∵点经过的路径长为,
∴,,
∴,
,
,
,
③当点在上时,
∵正方形边长为4,为中点,
∴,
∵点经过的路径长为,
∴,,
∴,
综上所述:与的函数表达式为:
.
故答案为C.
【点评】本题考查动点问题的函数图象,解决动点问题的函数图象问题关键是发现y随x的变化而变化的趋势.
11.【分析】根据二次根式的性质和分式的意义,被开方数≥0,分母≠0,可以求出x的范围.
解:根据题意得:x+2≥0且x-3≠0,
解得:x≥-2且x≠3.
【点评】本题考查的知识点为:分式有意义,分母不为0;二次根式的被开方数是非负数.注意二次根式也在分母上时,被开方数应大于0;两个解集,同大取大.
12.【分析】根据第二象限的点符号是“-,+”,m取负数即可.
解:∵点P(m,2)在第二象限内,
∴,
m取负数即可,如m=-1,
故答案为:-1(答案不唯一,负数即可).
【点评】本题考查了已知点所在象限求参数,属于基础题,掌握第二象限点坐标的符号是“-,+”是解题的关键.
13.【分析】由题意点P(x,y)的坐标满足x+y=xy,当x=2时,代入得到2+y=2y,求出y即可.
解:∵点P(x,y)的坐标满足x+y=xy,
当x=2时,代入得:2+y=2y,
∴y=2,
故答案为(2,2).
【点评】本题考查了和谐点的性质及等式求解,比较简单
14.【分析】容器内的水高=容器内原来的水高10cm+放入长方体铁块后增加的水高,依此列式即可.
解:由题意,得y=10+1×1×x÷(2×2)
即y=x+10.
故答案为y=x+10.
【点评】本题考查了根据实际问题列一次函数关系式,正确表示放入长方体铁块后增加的水高是解题的关键.
15.【分析】首先设当40≤t≤60时,距离y(千米)与时间t(分钟)的函数关系为y=kt+b,然后再把(40,2)(60,0)代入可得关于k、b的方程组,解出k、b的值,进而可得函数解析式,再把t=45代入即可.
解:设当40≤t≤60时,距离y(千米)与时间t(分钟)的函数关系为y=kt+b.
∵图象经过(40,2)(60,0),
∴,解得:,
∴y与t的函数关系式为y=﹣,
当t=45时,y=﹣×45+6=1.5.
故答案为1.5.
【点评】本题主要考查了一次函数的应用,关键是正确理解题意,掌握待定系数法求出函数解析式.
16.【分析】根据题意可以得到关于t的方程,从而可以求得点P的坐标,本题得以解决.
解:
由题意可得,150t=240(t﹣12),
解得,t=32,
则150t=150×32=4800,
∴点P的坐标为(32,4800),
故答案为(32,4800).
【点评】本题考查了一次函数的应用,根据题意列出方程150t=240(t﹣12)是解决问题的关键.
17.【分析】如图作ND∥x轴交y轴于D,作NC∥y轴交x轴于C.MN交y轴于K.利用全等三角形的性质,平行四边形的性质求出OC、OD即可;
解:如图作ND∥x轴交y轴于D,作NC∥y轴交x轴于C.MN交y轴于K.
∵NK=MK,∠DNK=∠BMK,∠NKD=∠MKB,
∴△NDK≌△MBK,
∴DN=BM=OC=3,DK=BK,
在Rt△KBM中,BM=3,∠MBK=60°,
∴∠BMK=30°,
∴DK=BK=BM=,
∴OD=5,
∴N(-3,5),
故答案为(-3,5)
【点评】本题考查坐标与图形变化,轴对称等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.
18.【分析】(1)由图象可知,蓄电池剩余电量为35千瓦时时汽车已行驶了150千米,据此即可求出1千瓦时的电量汽车能行驶的路程;
(2)运用待定系数法求出y关于x的函数表达式,再把x=180代入即可求出当汽车已行驶180千米时,蓄电池的剩余电量.
解:(1)由图像可知,蓄电池剩余电量为35千瓦时时汽车行驶了150千米.
1千瓦时可行驶千米.
(2)设,把点,代入,
得,∴,∴.
当时,.
答:当时,函数表达式为,当汽车行驶180千米时,蓄电池剩余电量为20千瓦时.
【点评】本题考查了一次函数的应用,解题的关键:(1)熟练运用待定系数法就解析式;(2)找出剩余油量相同时行驶的距离.本题属于基础题,难度不大,解决该类问题应结合图形,理解图形中点的坐标代表的意义.
19.【分析】(1)设关于的函数解析式是,把(0,6)(15,3)代入即可求解;(2)分别求出当时,当时x的值即可比较.
解:(1)设关于的函数解析式是,
,解得,,
即关于的函数解析式是;
(2)当时,,得,
当时,,得,
∵,
∴甲先到达地面.
【点评】此题主要考查一次函数的应用,解题的关键是根据题意求出一次函数解析式进行求解.
20.【分析】(1)利用描点法画出图形即可判断.
(2)设函数关系式为y=kx+b,利用待定系数法解决问题即可.
解:(1)观察图象可知:x=7,y=2.75这组数据错误.
(2)设y=kx+b,把x=1,y=0.75,x=2,y=1代入可得,
解得,
∴,
当x=16时,y=4.5,
答:秤杆上秤砣到秤纽的水平距离为16厘米时,秤钩所挂物重是4.5斤.
【点评】此题考查画一次函数的图象的方法,待定系数法求一次函数的解析式,一次函数的实际应用,正确计算是解此题的关键.
21.【分析】(1)根据高度每增加1百米,气温大约降低0.6℃,由3百米时温度为13.2°C,即可得出高度为5百米时的气温;
(2)应用待定系数法解答即可;
(3)根据(2)T=-0.6h+15的结论,将T=6代入,解答即可.
解:(1)由题意得 高度增加2百米,则温度降低2×0.6=1.2(℃).
∴13.2-1.2=12
∴高度为5百米时的气温大约是12℃.
(2)设T=-0.6h+b(k≠0),
当h=3时,T=13.2,
13.2=-0.63+b,
解得 b=15.
∴T=-0.6h+15.
(3)当T=6时,6=-0.6h+15,
解得h=15.
∴该山峰的高度大约为15百米.
【点评】本题考查一次函数的应用,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答问题.
22.【分析】(1)根据函数的概念进行解答;
(2)通过识图读取相关信息;
(3)根据图像信息进行解答.
解:(1)是的函数.
在这个变化过程中,对于的每一个确定的值,都有唯一确定的值与之对应.
(2)“加速期”结束时,小斌的速度为10.4m/s.
(3)答案不唯一.例如:根据图象信息,小斌在80米左右时速度下降明显,建议增加耐力训练,提高成绩.
【点评】本题考查通过函数图像读取信息,理解函数的概念,准确识图是解题关键.
23.【分析】(1)直接利用I号无人机从海拔10m处出发,以10m/min的速度匀速上升,求出其5分钟后的高度即可;
(2)将I号无人机的高度表达式减去II号无人机高度表达式,令其值为28,求解即可.
解:(1).
设,
将,代入得:
,
∴;
.
(2)令,
解得,满足题意;
无人机上升12min,I号无人机比II号无人机高28米.
【点评】本题考查了一次函数的实际应用,涉及到了求一次函数的表达式,两个一次函数值之间的比较等内容,解决本题的关键是读懂题意,与图形建立关联,能建立高度的表达式等,本题着重于对函数概念的理解与应用,考查了学生的基本功.
24.【分析】(1)m的值可以从图象上直接读取,n的值可以根据方案A和方案B的费用差和流量差相除求得;
(2)直接运用待定系数法求解即可;
(3)计算出方案C的图象与方案B的图象的交点表示的数值即可求解.
解:(1)
.
(2)设函数表达式为,
把,代入,得
,
解得,
∴y关于x的函数表达式.
(注:x的取值范围对考生不作要求)
(3)(兆).
由图象得,当每月使用的流量超过3772兆时,选择C方案最划算.
【点评】本题考查一次函数的应用,解答本题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.
25.【分析】(1)设y=kx+b,运用待定系数法求解即可;
(2)把y=1500代入(1)的结论即可;
(3)设小聪坐上了第n班车,30-25+10(n-1)≥40,解得n≥4.5,可得小聪坐上了第5班车,再根据“路程、速度与时间的关系”解答即可.
(1)解:由题意得,可设函数表达式为:.
把,代入,得,
解得.
∴第一班车离入口处的路程(米)与时间(分)的函数表达式为.
(2)解:把代入,解得,
(分).
∴第一班车到塔林所需时间10分钟.
(3)解:设小聪坐上第班车.
,解得,
∴小聪最早坐上第5班车.
等班车时间为5分钟,
坐班车所需时间:(分),
∴步行所需时间:(分),
(分).
∴小聪坐班车去草甸比他游玩结束后立即步行到达草甸提早7分钟
【点评】本题主要考查了一次函数的应用,熟练掌握待定系数法求出函数解析式是解答本题的关键.
26.【分析】(1)根据函数图象中的数据可以求得甲步行的速度和乙出发时甲离开小区的路程;
(2)根据函数图象中的数据可以求得OA的函数解析式,然后将x=18代入OA的函数解析式,即可求得点E的纵坐标,进而可以求得乙骑自行车的速度和乙到达还车点时甲、乙两人之间的距离;
(3)根据题意可以求得乙到达学校的时间,从而可以函数图象补充完整.
解:(1)由题意,得:甲步行的速度是 (米/分),
∴乙出发时甲离开小区的路程是 (米).
(2)设直线的解析式为:,
∵直线过点,
∴,
解得,
∴直线的解析式为:.
∴当时,,
∴乙骑自行车的速度是 (米/分).
∵乙骑自行车的时间为 (分),
∴乙骑自行车的路程为 (米).
当时,甲走过的路程是 (米),
∴乙到达还车点时,甲、乙两人之间的距离是 (米).
(3)乙步行的速度为:80-5=75(米/分),
乙到达学校用的时间为:25+(2700-2400)÷75=29(分),
当25≤x≤30时s关于x的函数的大致图象如图所示.
【点评】本题考查一次函数的应用,解答本题的关键是明确题意,利用一次函数的性质和数形结合的思想解答.
27.【分析】(1)设乙食材每千克进价为元,根据用80元购买的甲食材比用20元购买的乙食材多1千克列分式方程即可求解;
(2)①设每日购进甲食材千克,乙食材千克.根据每日用18000元购进甲、乙两种食材并恰好全部用完,利用进货总金额为180000元,含铁量一定列出二元一次方程组即可求解;
②设为包,根据题意,可以得到每日所获总利润与m的函数关系式,再根据A的数量不低于B的数量,可以得到m的取值范围,从而可以求得总利润的最大值.
解:(1)设乙食材每千克进价为元,则甲食材每千克进价为元,
由题意得,解得.
经检验,是所列方程的根,且符合题意.
(元).
答:甲、乙两种食材每千克进价分别为40元、20元.
(2)①设每日购进甲食材千克,乙食材千克.
由题意得,解得
答:每日购进甲食材400千克,乙食材100千克.
②设为包,则为包.
记总利润为元,则
.
的数量不低于的数量,
,.
,随的增大而减小。
当时,的最大值为2800元.
答:当为400包时,总利润最大.最大总利润为2800元.
【点评】本题主要考查了一次函数的应用、分式方程、二元一次方程的应用,解答本题时要明确题意、弄清表格数据的意义及各种量之间关系,利用方程的求未知量和一次函数的性质解答,注意分式方程要检验.
试卷第8页,共9页
试卷第1页,共9页
同课章节目录
