3.1从算式到方程 课后综合练 2021-2022学年七年级数学上册人教版(Word版含答案)
文档属性
| 名称 | 3.1从算式到方程 课后综合练 2021-2022学年七年级数学上册人教版(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-27 09:22:07 | ||
图片预览




文档简介
3.1从算式到方程【课后综合练】
-2021-2022学年七年级数学上册(人教版)
一、选择题
1、下列式子中是方程的是( )
A. B. C. D.
2、在方程①3x+y=4,②2x﹣=5,③3y+2=2﹣y,④2x2﹣5x+6=2(x2+3x)中,是一元一次方程的个数为( )
A.1个 B.2个 C.3个 D.4个
3、如果关于x的方程(m+1)x2+(m﹣1)x+m=0是一元一次方程,则m的值为( )
A.1 B.﹣1 C.0 D.1或﹣1
4、下列运用等式的性质对等式进行的变形中,错误的是( )
A.若a=b,则-2a=-2b B.若a2=b2 ,则a=b
C.若a=b,则 D.若x﹣3=y﹣3,则x=y
5、下列利用等式的性质解方程中,正确的是( )
A.由,得 B.,得
C.由,得 D.由,得
6、已知x=3是关于x的方程的解,则的值是( )
A.2 B.-2 C.1 D.﹣1
7、小亮在做作业时,不小心把方程中的一个常数污染了看不清,被污染的方程为:,他翻看答案,解为,请你帮他补出这个常数是( )
A. B.8 C. D.12
8、设■,●,▲分别表示三种不同的物体,如图所示,前两架天平保持平衡,如果要使第三架天平也平衡,那么以下方案不正确的是( )
A. B. C. D.
9、根据“的3倍与5的和比的少2”列出的方程是( )
A. B. C. D.
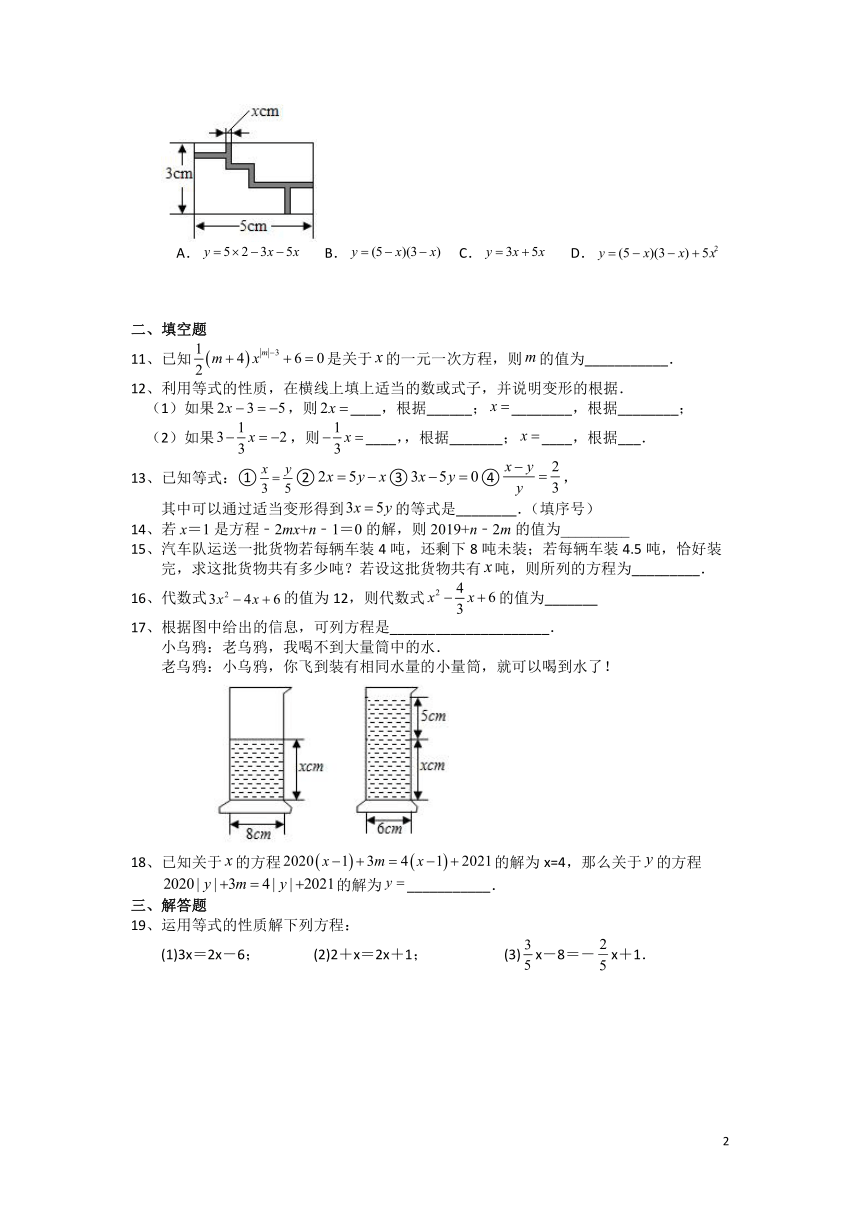
10、如图是一个迷宫游戏盘的局部平面简化示意图,该矩形的长、宽分别为,其中阴影部分为迷宫中的挡板,设挡板的宽度为,小球滚动的区域(空白区域)面积为,则下列所列方程正确的是( )
A. B. C. D.
二、填空题
11、已知是关于的一元一次方程,则的值为___________.
12、利用等式的性质,在横线上填上适当的数或式子,并说明变形的根据.
(1)如果,则____,根据______;________,根据________;
(2)如果,则____,,根据_______;____,根据___.
13、已知等式:①②③④,
其中可以通过适当变形得到的等式是________.(填序号)
14、若x=1是方程﹣2mx+n﹣1=0的解,则2019+n﹣2m的值为_________
15、汽车队运送一批货物若每辆车装4吨,还剩下8吨未装;若每辆车装4.5吨,恰好装完,求这批货物共有多少吨?若设这批货物共有吨,则所列的方程为_________.
16、代数式的值为12,则代数式的值为_______
17、根据图中给出的信息,可列方程是_____________________.
小乌鸦:老乌鸦,我喝不到大量筒中的水.
老乌鸦:小乌鸦,你飞到装有相同水量的小量筒,就可以喝到水了!
18、已知关于的方程的解为x=4,那么关于的方程的解为___________.
三、解答题
19、运用等式的性质解下列方程:
(1)3x=2x-6; (2)2+x=2x+1; (3)x-8=-x+1.
20、阅读理解题:
下面是小明将等式x﹣4=3x﹣4进行变形的过程:
x﹣4+4=3x﹣4+4,①
x=3x,②
1=3.③
(1)小明①的依据是 ________________________ .
(2)小明出错的步骤是 ,错误的原因是 _______ .
(3)给出正确的解法.
21、已知是方程的解,
(1)求的值;
(2)检验是不是方程的解.
22、老师在黑板上写了一个等式.王聪说,刘敏说不一定,当时,这个等式也可能成立.
(1)你认为他们俩的说法正确吗?请说明理由;
(2)你能求出当时中x的值吗?
23、根据下列题干设未知数列方程,并判断它是不是一元一次方程.
(1)从60cm的木条上截去2段同样长的木棒,还剩下10cm长的短木条,截下的每段为多少?
(2)小红对小敏说:“我是6月份出生的,我的年龄的2倍加上10,结果正好是我出生的那个月的
总天数,你猜我有几岁?”
24、重温例题:
小丽在水果店花18元买了苹果和橘子共6千克,已知苹果每千克3.2元,橘子每千克2.6元.小丽买了苹果和橘子各多少千克?
解决问题:
(1)设所购买的苹果质量为xkg.请你将下列同学的探究过程补充完整.
①小明同学列出了下表,并根据相等关系“买苹果的金额+买橘子的金额=18元”,
可得方程: .
单价(元/kg) 质量(kg) 金额(元)
苹果 3.2 x 3.2x
橘子 2.6 6﹣x 2.6(6﹣x)
合计 6 18
②小红、小王、小颖三位同学分别给出了不同于小明同学的表格和方程,请补充完整.
(友情提醒:表格中的空格表达式不同于小明所填的,所列方程不要化简.)
i小红根据相等关系“所买苹果的质量+橘子的质量=6kg”,得方程 .
单价(元/kg) 质量(kg) 金额(元)
苹果 3.2 x 3.2x
橘子 2.6 18﹣3.2x
合计 6 18
ii小王根据相等关系“苹果的单价×其质量=苹果购买金额”,得方程 .
单价(元/kg) 质量(kg) 金额(元)
苹果 3.2 x
橘子 2.6 6﹣x 2.6(6﹣x)
合计 6 18
iii小颖根据相等关系“橘子的单价×其质量=橘子购买金额”,得方程 .
单价(元/kg) 质量(kg) 金额(元)
苹果 3.2 x 3.2x
橘子 2.6 6﹣x
合计 6 18
(2)设苹果购买金额为y元,下列方程正确的是 .(填写正确的序号)
①; ②y+2.6(6)=18;
③3.2(6)=y; ④3.2(6)=18﹣y.
3.1从算式到方程【课后综合练】
-2021-2022学年七年级数学上册(人教版)(解析)
一、选择题
1、下列式子中是方程的是( )
A. B. C. D.
【答案】B
【分析】本题主要考查的是方程的定义,含有未知数的等式叫方程,据此可得出正确答案.
【解析】A、不是方程,因为它不含有未知数,本选项错误;
B、是方程,是未知数,式子又是等式,本选项正确;
C、虽然含有未知数,但不是等式,故不是方程,本选项错误;
D、虽然含有未知数,但不是等式,故不是方程,本选项错误.
故选:B.
2、在方程①3x+y=4,②2x﹣=5,③3y+2=2﹣y,④2x2﹣5x+6=2(x2+3x)中,是一元一次方程的个数为( )
A.1个 B.2个 C.3个 D.4个
【分析】只含有一个未知数(元),并且未知数的指数是1(次)的方程叫做一元一次方程.它的一般形式是ax+b=0(a,b是常数且a≠0).
【答案】解:①3x+y=4中含有2个未知数,属于二元一次方程,不符合题意,
②2x﹣=5是分式方程,不符合题意;
③3y+2=2﹣y符合一元一次方程的定义,符合题意;
④由2x2﹣5x+6=2(x2+3x)得到:﹣11x+6=0符合一元一次方程的定义,符合题意;
故选:B.
3、如果关于x的方程(m+1)x2+(m﹣1)x+m=0是一元一次方程,则m的值为( )
A.1 B.﹣1 C.0 D.1或﹣1
【分析】由一元一次方程的定义可知:m+1=0,从而可求得m的值.
【答案】解:∵关于x的方程(m+1)x2+(m﹣1)x+m=0是一元一次方程,
∴m+1=0.
解得:m=﹣1.
故选:B.
4、下列运用等式的性质对等式进行的变形中,错误的是( )
A.若a=b,则-2a=-2b B.若a2=b2 ,则a=b
C.若a=b,则 D.若x﹣3=y﹣3,则x=y
【答案】B
【分析】根据等式的性质,对选项逐个判断即可.
【详解】解:∵∴,,等式两边同时乘以或除以同一个数,等式仍然成立;
∴A、C选项正确,不符合题意;
∵∴,等式两边同时加上同一个数,等式仍然成立;∴D选项正确,不符合题意
∵∴或∴B选项错误,符合题意;故选B
5、下列利用等式的性质解方程中,正确的是( )
A.由,得 B.,得
C.由,得 D.由,得
【答案】D
【分析】根据一元一次方程的解法解题即可.
【解析】A. 由,得x=11,该选项错误. B. ,得,该选项错误.
C. 由,得,该选项错误. D. 由,得,该选项正确.故选D.
6、已知x=3是关于x的方程的解,则的值是( )
A.2 B.-2 C.1 D.﹣1
【答案】A
【分析】把x=3代入方程,可得n-2m=1,进而即可求解.
【详解】解:∵x=3是关于x的方程的解,
∴6m=3n-3,即:n-2m=1,∴=2,故选A.
7、小亮在做作业时,不小心把方程中的一个常数污染了看不清,被污染的方程为:,他翻看答案,解为,请你帮他补出这个常数是( )
A. B.8 C. D.12
【答案】B
【分析】将代入被污染的方程,即可求出污染处的常数.
【解析】将代入被污染的方程,得:
解得:
故选B
8、设■,●,▲分别表示三种不同的物体,如图所示,前两架天平保持平衡,如果要使第三架天平也平衡,那么以下方案不正确的是( )
A. B. C. D.
【分析】根据第一个天平可得2●=▲+■,根据第二个天平可得●+▲=■,可得出答案.
【解答】解:根据图示可得:2●=▲+■①,
●+▲=■②,
由①②可得●=2▲,■=3▲,
则■+●=5▲=2●+▲=●+3▲.
故选:A.
9、根据“的3倍与5的和比的少2”列出的方程是( )
A. B. C. D.
【解析】:x的3倍与5的和是指3x+5,x的是指x,则根据题意可得:3x+5=x-2
故选A
10、如图是一个迷宫游戏盘的局部平面简化示意图,该矩形的长、宽分别为,其中阴影部分为迷宫中的挡板,设挡板的宽度为,小球滚动的区域(空白区域)面积为,则下列所列方程正确的是( )
A. B. C. D.
【答案】B
【分析】设挡板的宽度为x cm,小球滚动的区域(空白区域)面积为y cm2,根据题意列出方程解答即可.
【详解】解:设挡板的宽度为x cm,小球滚动的区域(空白区域)面积为y cm2,根据题意可得:
y=(5-x)(3-x),故选:B.
二、填空题
11、已知是关于的一元一次方程,则的值为___________.
【答案】4
【分析】根据一元一次方程的定义判断即可.
【详解】解:∵是关于的一元一次方程,
∴且,解得:,故答案为:4.
12、利用等式的性质,在横线上填上适当的数或式子,并说明变形的根据.
(1)如果,则____,根据______;________,根据________;
(2)如果,则____,,根据_______;____,根据___.
【答案】(1)-2 等式的基本性质1 -1 等式的基本性质2
(2)-5 等式的基本性质1 15 等式的基本性质2
【分析】(1)先由等式的性质1得出,再由等式的性质2即可得出结论;
(2)先由等式的性质1得出,再由等式的性质2即可得出结论.
【详解】解:(1)方程两边同时加,得:,
方程两边同时除以,得:,
故答案为:;等式的基本性质;;等式的基本性质;
(2)方程两边同时减,得:,
方程两边同时乘以,得:,
故答案为:;等式的基本性质;;等式的基本性质.
13、已知等式:①②③④,
其中可以通过适当变形得到的等式是________.(填序号)
【分析】利用等式的性质对每个式子进行变形即可找出答案.
【详解】
解:①根据等式性质2,由两边同乘以15得,5x= 3y;
②根据等式性质1,两边同加x得,;
③根据等式性质1,两边同加5y得,;
④根据等式性质2,由两边同乘以3y得,据等式性质1,两边同加3y得,.
故答案为:②③④.
14、若x=1是方程﹣2mx+n﹣1=0的解,则2019+n﹣2m的值为_________
【分析】把x=1代入方程求出2m﹣n的值,原式变形后代入计算即可求出值.
【解答】解:把x=1代入方程得:﹣2m+n﹣1=0,
整理得:2m﹣n=﹣1,
则原式=2019+n﹣2m=2019﹣(2m﹣n)=2019﹣(﹣1)=2019+1=2020,
15、汽车队运送一批货物若每辆车装4吨,还剩下8吨未装;若每辆车装4.5吨,恰好装完,求这批货物共有多少吨?若设这批货物共有吨,则所列的方程为_________.
【分析】设这批货物共有x吨,根据题意可知等量关系为:两种装法中车辆的数量是一定的,据此列方程.
【详解】
解:设这批货物共有x吨,
由题意得,.
故答案为:.
16、代数式的值为12,则代数式的值为_______
【分析】
由题意可得到,等式两边同时除以3得到,然后代入求解即可.
【详解】
解:∵由题意可知:,
∴,
∴,
∴=2+6=8,
17、根据图中给出的信息,可列方程是_____________________.
小乌鸦:老乌鸦,我喝不到大量筒中的水.
老乌鸦:小乌鸦,你飞到装有相同水量的小量筒,就可以喝到水了!
【解析】解:由题意可得:π×()2 x=π×()2×(x+5),
故答案为:π×()2 x=π×()2×(x+5).
【答案】π×()2 x=π×()2×(x+5)
18、已知关于的方程的解为x=4,那么关于的方程的解为___________.
【答案】
【分析】结合题意,根据一元一次方程和绝对值的性质计算,即可得到答案.
【详解】解:∵关于的方程的解为x=4∴
∵,且 ∴ ∴故答案为:.
三、解答题
19、运用等式的性质解下列方程:
(1)3x=2x-6; (2)2+x=2x+1; (3)x-8=-x+1.
【答案】(1)x=-6;(2)x=1;(3)x=9
【分析】
(1)根据等式的性质:方程两边都减2x,可得答案;
(2)根据等式的性质:方程两边都减x,化简后方程的两边都减1,可得答案.
(3)根据等式的性质:方程两边都加x,化简后方程的两边都加8,可得答案.
【详解】
(1)两边减2x,得3x-2x=2x-6-2x.
所以x=-6.
(2)两边减x,得2+x-x=2x+1-x.
化简,得2=x+1.
两边减1,得2-1=x+1-1
所以x=1.
(3)两边加x,
得x-8+x=-x+1+x.
化简,得x-8=1.
两边加8,得x-8+8=1+8.
所以x=9.
20、阅读理解题:
下面是小明将等式x﹣4=3x﹣4进行变形的过程:
x﹣4+4=3x﹣4+4,①
x=3x,②
1=3.③
(1)小明①的依据是 ________________________ .
(2)小明出错的步骤是 ,错误的原因是 _______ .
(3)给出正确的解法.
【答案】(1)等式的两边都加(或减)同一个数(或整式),结果仍得等式;(2)③,等式两边都除以0;(3)见解析.
【分析】(1)根据等式的基本性质即可解答;(2)根据等式的基本性质即可解答;
(3)按照移项、合并同类项、系数化为一的步骤解答即可.
【详解】(1)小明①的依据是等式的两边都加(或减)同一个数(或整式),结果仍得等式;
故答案为:等式的两边都加(或减)同一个数(或整式),结果仍得等式;
(2)小明出错的步骤是③,错误的原因是等式两边都除以0;
故答案为:③;等式两边都除以0.
(3)x﹣4=3x﹣4,
x﹣4+4=3x﹣4+4,
x=3x,
x﹣3x=0,
﹣2x=0,
x=0.
21、已知是方程的解,
(1)求的值;
(2)检验是不是方程的解.
【答案】(1)a=2;(2)不是
【分析】(1)根据方程的根的定义,即可求解;
(2)把a=2,代入,检验方程左右的值是否相等,即可得到答案.
【详解】(1)∵x=2是方程ax-4=0的解,
∴把x=2代入ax-4=0得:2a-4=0,解得:a=2;
(2)将a=2代入方程2ax-5=3x-4a,得:4x-5=3x-8,
将x=3代入该方程左边,则左边=7,代入右边,则右边=1,
∵左边≠右边,∴x=3不是方程4x-5=3x-8的解.
22、老师在黑板上写了一个等式.王聪说,刘敏说不一定,当时,这个等式也可能成立.
(1)你认为他们俩的说法正确吗?请说明理由;
(2)你能求出当时中x的值吗?
(1)王聪的说法不正确,见解析;(2)
【分析】
(1)根据等式的性质进行判断即可.
(2)利用代入法求解即可.
【详解】
(1)王聪的说法不正确.
理由:两边除以不符合等式的性质2,因为当时,x为任意实数.
刘敏的说法正确.
理由:因为当时,x为任意实数,所以当时,这个等式也可能成立.
(2)将代入,得,解得.
23、根据下列题干设未知数列方程,并判断它是不是一元一次方程.
(1)从60cm的木条上截去2段同样长的木棒,还剩下10cm长的短木条,截下的每段为多少?
(2)小红对小敏说:“我是6月份出生的,我的年龄的2倍加上10,结果正好是我出生的那个月的
总天数,你猜我有几岁?”
【答案】(1) 60-2x=10,是一元一次方程;(2) 2x+10=30,是一元一次方程.
【分析】
(1)根据等量关系:木条截取两段后剩下的长度等于10cm,即可列出方程,
(2)根据等量关系:我的年龄的2倍加上10等于我出生的那个月的总天数,即可列出方程.
【详解】
(1)设截下的每段为xcm,根据题意可列出方程为:60-2x=10,
(2)设小红的岁数为x,根据题意可列出方程为:2x+10=30.
(1)(2)都是一元一次方程.
24、重温例题:
小丽在水果店花18元买了苹果和橘子共6千克,已知苹果每千克3.2元,橘子每千克2.6元.小丽买了苹果和橘子各多少千克?
解决问题:
(1)设所购买的苹果质量为xkg.请你将下列同学的探究过程补充完整.
①小明同学列出了下表,并根据相等关系“买苹果的金额+买橘子的金额=18元”,
可得方程: .
单价(元/kg) 质量(kg) 金额(元)
苹果 3.2 x 3.2x
橘子 2.6 6﹣x 2.6(6﹣x)
合计 6 18
②小红、小王、小颖三位同学分别给出了不同于小明同学的表格和方程,请补充完整.
(友情提醒:表格中的空格表达式不同于小明所填的,所列方程不要化简.)
i小红根据相等关系“所买苹果的质量+橘子的质量=6kg”,得方程 .
单价(元/kg) 质量(kg) 金额(元)
苹果 3.2 x 3.2x
橘子 2.6 18﹣3.2x
合计 6 18
ii小王根据相等关系“苹果的单价×其质量=苹果购买金额”,得方程 .
单价(元/kg) 质量(kg) 金额(元)
苹果 3.2 x
橘子 2.6 6﹣x 2.6(6﹣x)
合计 6 18
iii小颖根据相等关系“橘子的单价×其质量=橘子购买金额”,得方程 .
单价(元/kg) 质量(kg) 金额(元)
苹果 3.2 x 3.2x
橘子 2.6 6﹣x
合计 6 18
(2)设苹果购买金额为y元,下列方程正确的是 .(填写正确的序号)
①; ②y+2.6(6)=18;
③3.2(6)=y; ④3.2(6)=18﹣y.
【分析】(1)根据“苹果质量+橘子质量=6kg,苹果单价×苹果质量=苹果购买金额和橘子的单价×其质量=橘子购买金额”填表、列出方程即可;
(2)分别根据“苹果质量+橘子质量=6kg和苹果单价×苹果质量=苹果购买金额”可得答案.
【解析】(1)①设小丽买了x千克的苹果,则她买橘子(6﹣x)千克.
由题意得:3.2x+2.6(6﹣x)=18;
故答案为:3.2x+2.6(6﹣x)=18;
②i补全表格如下:
单价(元/kg) 质量(kg) 金额(元)
苹果 3.2 x 3.2x
橘子 2.6 18﹣3.2x
合计 6 18
根据相等关系“所买苹果的质量+橘子的质量=6kg”,得方程:x+=6,
故答案为:x+=6;
ii补全表格如下:
单价(元/kg) 质量(kg) 金额(元)
苹果 3.2 x 18﹣2.6(6﹣x)
橘子 2.6 6﹣x 2.6(6﹣x)
合计 6 18
根据相等关系“苹果的单价×其质量=苹果购买金额”,得方程:3.2x=18﹣2.6(6﹣x),
故答案为:3.2x=18﹣2.6(6﹣x).
iii补全表格如下:
单价(元/kg) 质量(kg) 金额(元)
苹果 3.2 x 3.2x
橘子 2.6 6﹣x 18﹣3.2x
合计 6 18
根据相等关系“橘子的单价×其质量=橘子购买金额”,得方程:2.6(6﹣x)=18﹣3.2x,
故答案为:2.6(6﹣x)=18﹣3.2x.
(2)设苹果购买金额为y元,所列方程正确的是①③,
故答案为:①③.
-2021-2022学年七年级数学上册(人教版)
一、选择题
1、下列式子中是方程的是( )
A. B. C. D.
2、在方程①3x+y=4,②2x﹣=5,③3y+2=2﹣y,④2x2﹣5x+6=2(x2+3x)中,是一元一次方程的个数为( )
A.1个 B.2个 C.3个 D.4个
3、如果关于x的方程(m+1)x2+(m﹣1)x+m=0是一元一次方程,则m的值为( )
A.1 B.﹣1 C.0 D.1或﹣1
4、下列运用等式的性质对等式进行的变形中,错误的是( )
A.若a=b,则-2a=-2b B.若a2=b2 ,则a=b
C.若a=b,则 D.若x﹣3=y﹣3,则x=y
5、下列利用等式的性质解方程中,正确的是( )
A.由,得 B.,得
C.由,得 D.由,得
6、已知x=3是关于x的方程的解,则的值是( )
A.2 B.-2 C.1 D.﹣1
7、小亮在做作业时,不小心把方程中的一个常数污染了看不清,被污染的方程为:,他翻看答案,解为,请你帮他补出这个常数是( )
A. B.8 C. D.12
8、设■,●,▲分别表示三种不同的物体,如图所示,前两架天平保持平衡,如果要使第三架天平也平衡,那么以下方案不正确的是( )
A. B. C. D.
9、根据“的3倍与5的和比的少2”列出的方程是( )
A. B. C. D.
10、如图是一个迷宫游戏盘的局部平面简化示意图,该矩形的长、宽分别为,其中阴影部分为迷宫中的挡板,设挡板的宽度为,小球滚动的区域(空白区域)面积为,则下列所列方程正确的是( )
A. B. C. D.
二、填空题
11、已知是关于的一元一次方程,则的值为___________.
12、利用等式的性质,在横线上填上适当的数或式子,并说明变形的根据.
(1)如果,则____,根据______;________,根据________;
(2)如果,则____,,根据_______;____,根据___.
13、已知等式:①②③④,
其中可以通过适当变形得到的等式是________.(填序号)
14、若x=1是方程﹣2mx+n﹣1=0的解,则2019+n﹣2m的值为_________
15、汽车队运送一批货物若每辆车装4吨,还剩下8吨未装;若每辆车装4.5吨,恰好装完,求这批货物共有多少吨?若设这批货物共有吨,则所列的方程为_________.
16、代数式的值为12,则代数式的值为_______
17、根据图中给出的信息,可列方程是_____________________.
小乌鸦:老乌鸦,我喝不到大量筒中的水.
老乌鸦:小乌鸦,你飞到装有相同水量的小量筒,就可以喝到水了!
18、已知关于的方程的解为x=4,那么关于的方程的解为___________.
三、解答题
19、运用等式的性质解下列方程:
(1)3x=2x-6; (2)2+x=2x+1; (3)x-8=-x+1.
20、阅读理解题:
下面是小明将等式x﹣4=3x﹣4进行变形的过程:
x﹣4+4=3x﹣4+4,①
x=3x,②
1=3.③
(1)小明①的依据是 ________________________ .
(2)小明出错的步骤是 ,错误的原因是 _______ .
(3)给出正确的解法.
21、已知是方程的解,
(1)求的值;
(2)检验是不是方程的解.
22、老师在黑板上写了一个等式.王聪说,刘敏说不一定,当时,这个等式也可能成立.
(1)你认为他们俩的说法正确吗?请说明理由;
(2)你能求出当时中x的值吗?
23、根据下列题干设未知数列方程,并判断它是不是一元一次方程.
(1)从60cm的木条上截去2段同样长的木棒,还剩下10cm长的短木条,截下的每段为多少?
(2)小红对小敏说:“我是6月份出生的,我的年龄的2倍加上10,结果正好是我出生的那个月的
总天数,你猜我有几岁?”
24、重温例题:
小丽在水果店花18元买了苹果和橘子共6千克,已知苹果每千克3.2元,橘子每千克2.6元.小丽买了苹果和橘子各多少千克?
解决问题:
(1)设所购买的苹果质量为xkg.请你将下列同学的探究过程补充完整.
①小明同学列出了下表,并根据相等关系“买苹果的金额+买橘子的金额=18元”,
可得方程: .
单价(元/kg) 质量(kg) 金额(元)
苹果 3.2 x 3.2x
橘子 2.6 6﹣x 2.6(6﹣x)
合计 6 18
②小红、小王、小颖三位同学分别给出了不同于小明同学的表格和方程,请补充完整.
(友情提醒:表格中的空格表达式不同于小明所填的,所列方程不要化简.)
i小红根据相等关系“所买苹果的质量+橘子的质量=6kg”,得方程 .
单价(元/kg) 质量(kg) 金额(元)
苹果 3.2 x 3.2x
橘子 2.6 18﹣3.2x
合计 6 18
ii小王根据相等关系“苹果的单价×其质量=苹果购买金额”,得方程 .
单价(元/kg) 质量(kg) 金额(元)
苹果 3.2 x
橘子 2.6 6﹣x 2.6(6﹣x)
合计 6 18
iii小颖根据相等关系“橘子的单价×其质量=橘子购买金额”,得方程 .
单价(元/kg) 质量(kg) 金额(元)
苹果 3.2 x 3.2x
橘子 2.6 6﹣x
合计 6 18
(2)设苹果购买金额为y元,下列方程正确的是 .(填写正确的序号)
①; ②y+2.6(6)=18;
③3.2(6)=y; ④3.2(6)=18﹣y.
3.1从算式到方程【课后综合练】
-2021-2022学年七年级数学上册(人教版)(解析)
一、选择题
1、下列式子中是方程的是( )
A. B. C. D.
【答案】B
【分析】本题主要考查的是方程的定义,含有未知数的等式叫方程,据此可得出正确答案.
【解析】A、不是方程,因为它不含有未知数,本选项错误;
B、是方程,是未知数,式子又是等式,本选项正确;
C、虽然含有未知数,但不是等式,故不是方程,本选项错误;
D、虽然含有未知数,但不是等式,故不是方程,本选项错误.
故选:B.
2、在方程①3x+y=4,②2x﹣=5,③3y+2=2﹣y,④2x2﹣5x+6=2(x2+3x)中,是一元一次方程的个数为( )
A.1个 B.2个 C.3个 D.4个
【分析】只含有一个未知数(元),并且未知数的指数是1(次)的方程叫做一元一次方程.它的一般形式是ax+b=0(a,b是常数且a≠0).
【答案】解:①3x+y=4中含有2个未知数,属于二元一次方程,不符合题意,
②2x﹣=5是分式方程,不符合题意;
③3y+2=2﹣y符合一元一次方程的定义,符合题意;
④由2x2﹣5x+6=2(x2+3x)得到:﹣11x+6=0符合一元一次方程的定义,符合题意;
故选:B.
3、如果关于x的方程(m+1)x2+(m﹣1)x+m=0是一元一次方程,则m的值为( )
A.1 B.﹣1 C.0 D.1或﹣1
【分析】由一元一次方程的定义可知:m+1=0,从而可求得m的值.
【答案】解:∵关于x的方程(m+1)x2+(m﹣1)x+m=0是一元一次方程,
∴m+1=0.
解得:m=﹣1.
故选:B.
4、下列运用等式的性质对等式进行的变形中,错误的是( )
A.若a=b,则-2a=-2b B.若a2=b2 ,则a=b
C.若a=b,则 D.若x﹣3=y﹣3,则x=y
【答案】B
【分析】根据等式的性质,对选项逐个判断即可.
【详解】解:∵∴,,等式两边同时乘以或除以同一个数,等式仍然成立;
∴A、C选项正确,不符合题意;
∵∴,等式两边同时加上同一个数,等式仍然成立;∴D选项正确,不符合题意
∵∴或∴B选项错误,符合题意;故选B
5、下列利用等式的性质解方程中,正确的是( )
A.由,得 B.,得
C.由,得 D.由,得
【答案】D
【分析】根据一元一次方程的解法解题即可.
【解析】A. 由,得x=11,该选项错误. B. ,得,该选项错误.
C. 由,得,该选项错误. D. 由,得,该选项正确.故选D.
6、已知x=3是关于x的方程的解,则的值是( )
A.2 B.-2 C.1 D.﹣1
【答案】A
【分析】把x=3代入方程,可得n-2m=1,进而即可求解.
【详解】解:∵x=3是关于x的方程的解,
∴6m=3n-3,即:n-2m=1,∴=2,故选A.
7、小亮在做作业时,不小心把方程中的一个常数污染了看不清,被污染的方程为:,他翻看答案,解为,请你帮他补出这个常数是( )
A. B.8 C. D.12
【答案】B
【分析】将代入被污染的方程,即可求出污染处的常数.
【解析】将代入被污染的方程,得:
解得:
故选B
8、设■,●,▲分别表示三种不同的物体,如图所示,前两架天平保持平衡,如果要使第三架天平也平衡,那么以下方案不正确的是( )
A. B. C. D.
【分析】根据第一个天平可得2●=▲+■,根据第二个天平可得●+▲=■,可得出答案.
【解答】解:根据图示可得:2●=▲+■①,
●+▲=■②,
由①②可得●=2▲,■=3▲,
则■+●=5▲=2●+▲=●+3▲.
故选:A.
9、根据“的3倍与5的和比的少2”列出的方程是( )
A. B. C. D.
【解析】:x的3倍与5的和是指3x+5,x的是指x,则根据题意可得:3x+5=x-2
故选A
10、如图是一个迷宫游戏盘的局部平面简化示意图,该矩形的长、宽分别为,其中阴影部分为迷宫中的挡板,设挡板的宽度为,小球滚动的区域(空白区域)面积为,则下列所列方程正确的是( )
A. B. C. D.
【答案】B
【分析】设挡板的宽度为x cm,小球滚动的区域(空白区域)面积为y cm2,根据题意列出方程解答即可.
【详解】解:设挡板的宽度为x cm,小球滚动的区域(空白区域)面积为y cm2,根据题意可得:
y=(5-x)(3-x),故选:B.
二、填空题
11、已知是关于的一元一次方程,则的值为___________.
【答案】4
【分析】根据一元一次方程的定义判断即可.
【详解】解:∵是关于的一元一次方程,
∴且,解得:,故答案为:4.
12、利用等式的性质,在横线上填上适当的数或式子,并说明变形的根据.
(1)如果,则____,根据______;________,根据________;
(2)如果,则____,,根据_______;____,根据___.
【答案】(1)-2 等式的基本性质1 -1 等式的基本性质2
(2)-5 等式的基本性质1 15 等式的基本性质2
【分析】(1)先由等式的性质1得出,再由等式的性质2即可得出结论;
(2)先由等式的性质1得出,再由等式的性质2即可得出结论.
【详解】解:(1)方程两边同时加,得:,
方程两边同时除以,得:,
故答案为:;等式的基本性质;;等式的基本性质;
(2)方程两边同时减,得:,
方程两边同时乘以,得:,
故答案为:;等式的基本性质;;等式的基本性质.
13、已知等式:①②③④,
其中可以通过适当变形得到的等式是________.(填序号)
【分析】利用等式的性质对每个式子进行变形即可找出答案.
【详解】
解:①根据等式性质2,由两边同乘以15得,5x= 3y;
②根据等式性质1,两边同加x得,;
③根据等式性质1,两边同加5y得,;
④根据等式性质2,由两边同乘以3y得,据等式性质1,两边同加3y得,.
故答案为:②③④.
14、若x=1是方程﹣2mx+n﹣1=0的解,则2019+n﹣2m的值为_________
【分析】把x=1代入方程求出2m﹣n的值,原式变形后代入计算即可求出值.
【解答】解:把x=1代入方程得:﹣2m+n﹣1=0,
整理得:2m﹣n=﹣1,
则原式=2019+n﹣2m=2019﹣(2m﹣n)=2019﹣(﹣1)=2019+1=2020,
15、汽车队运送一批货物若每辆车装4吨,还剩下8吨未装;若每辆车装4.5吨,恰好装完,求这批货物共有多少吨?若设这批货物共有吨,则所列的方程为_________.
【分析】设这批货物共有x吨,根据题意可知等量关系为:两种装法中车辆的数量是一定的,据此列方程.
【详解】
解:设这批货物共有x吨,
由题意得,.
故答案为:.
16、代数式的值为12,则代数式的值为_______
【分析】
由题意可得到,等式两边同时除以3得到,然后代入求解即可.
【详解】
解:∵由题意可知:,
∴,
∴,
∴=2+6=8,
17、根据图中给出的信息,可列方程是_____________________.
小乌鸦:老乌鸦,我喝不到大量筒中的水.
老乌鸦:小乌鸦,你飞到装有相同水量的小量筒,就可以喝到水了!
【解析】解:由题意可得:π×()2 x=π×()2×(x+5),
故答案为:π×()2 x=π×()2×(x+5).
【答案】π×()2 x=π×()2×(x+5)
18、已知关于的方程的解为x=4,那么关于的方程的解为___________.
【答案】
【分析】结合题意,根据一元一次方程和绝对值的性质计算,即可得到答案.
【详解】解:∵关于的方程的解为x=4∴
∵,且 ∴ ∴故答案为:.
三、解答题
19、运用等式的性质解下列方程:
(1)3x=2x-6; (2)2+x=2x+1; (3)x-8=-x+1.
【答案】(1)x=-6;(2)x=1;(3)x=9
【分析】
(1)根据等式的性质:方程两边都减2x,可得答案;
(2)根据等式的性质:方程两边都减x,化简后方程的两边都减1,可得答案.
(3)根据等式的性质:方程两边都加x,化简后方程的两边都加8,可得答案.
【详解】
(1)两边减2x,得3x-2x=2x-6-2x.
所以x=-6.
(2)两边减x,得2+x-x=2x+1-x.
化简,得2=x+1.
两边减1,得2-1=x+1-1
所以x=1.
(3)两边加x,
得x-8+x=-x+1+x.
化简,得x-8=1.
两边加8,得x-8+8=1+8.
所以x=9.
20、阅读理解题:
下面是小明将等式x﹣4=3x﹣4进行变形的过程:
x﹣4+4=3x﹣4+4,①
x=3x,②
1=3.③
(1)小明①的依据是 ________________________ .
(2)小明出错的步骤是 ,错误的原因是 _______ .
(3)给出正确的解法.
【答案】(1)等式的两边都加(或减)同一个数(或整式),结果仍得等式;(2)③,等式两边都除以0;(3)见解析.
【分析】(1)根据等式的基本性质即可解答;(2)根据等式的基本性质即可解答;
(3)按照移项、合并同类项、系数化为一的步骤解答即可.
【详解】(1)小明①的依据是等式的两边都加(或减)同一个数(或整式),结果仍得等式;
故答案为:等式的两边都加(或减)同一个数(或整式),结果仍得等式;
(2)小明出错的步骤是③,错误的原因是等式两边都除以0;
故答案为:③;等式两边都除以0.
(3)x﹣4=3x﹣4,
x﹣4+4=3x﹣4+4,
x=3x,
x﹣3x=0,
﹣2x=0,
x=0.
21、已知是方程的解,
(1)求的值;
(2)检验是不是方程的解.
【答案】(1)a=2;(2)不是
【分析】(1)根据方程的根的定义,即可求解;
(2)把a=2,代入,检验方程左右的值是否相等,即可得到答案.
【详解】(1)∵x=2是方程ax-4=0的解,
∴把x=2代入ax-4=0得:2a-4=0,解得:a=2;
(2)将a=2代入方程2ax-5=3x-4a,得:4x-5=3x-8,
将x=3代入该方程左边,则左边=7,代入右边,则右边=1,
∵左边≠右边,∴x=3不是方程4x-5=3x-8的解.
22、老师在黑板上写了一个等式.王聪说,刘敏说不一定,当时,这个等式也可能成立.
(1)你认为他们俩的说法正确吗?请说明理由;
(2)你能求出当时中x的值吗?
(1)王聪的说法不正确,见解析;(2)
【分析】
(1)根据等式的性质进行判断即可.
(2)利用代入法求解即可.
【详解】
(1)王聪的说法不正确.
理由:两边除以不符合等式的性质2,因为当时,x为任意实数.
刘敏的说法正确.
理由:因为当时,x为任意实数,所以当时,这个等式也可能成立.
(2)将代入,得,解得.
23、根据下列题干设未知数列方程,并判断它是不是一元一次方程.
(1)从60cm的木条上截去2段同样长的木棒,还剩下10cm长的短木条,截下的每段为多少?
(2)小红对小敏说:“我是6月份出生的,我的年龄的2倍加上10,结果正好是我出生的那个月的
总天数,你猜我有几岁?”
【答案】(1) 60-2x=10,是一元一次方程;(2) 2x+10=30,是一元一次方程.
【分析】
(1)根据等量关系:木条截取两段后剩下的长度等于10cm,即可列出方程,
(2)根据等量关系:我的年龄的2倍加上10等于我出生的那个月的总天数,即可列出方程.
【详解】
(1)设截下的每段为xcm,根据题意可列出方程为:60-2x=10,
(2)设小红的岁数为x,根据题意可列出方程为:2x+10=30.
(1)(2)都是一元一次方程.
24、重温例题:
小丽在水果店花18元买了苹果和橘子共6千克,已知苹果每千克3.2元,橘子每千克2.6元.小丽买了苹果和橘子各多少千克?
解决问题:
(1)设所购买的苹果质量为xkg.请你将下列同学的探究过程补充完整.
①小明同学列出了下表,并根据相等关系“买苹果的金额+买橘子的金额=18元”,
可得方程: .
单价(元/kg) 质量(kg) 金额(元)
苹果 3.2 x 3.2x
橘子 2.6 6﹣x 2.6(6﹣x)
合计 6 18
②小红、小王、小颖三位同学分别给出了不同于小明同学的表格和方程,请补充完整.
(友情提醒:表格中的空格表达式不同于小明所填的,所列方程不要化简.)
i小红根据相等关系“所买苹果的质量+橘子的质量=6kg”,得方程 .
单价(元/kg) 质量(kg) 金额(元)
苹果 3.2 x 3.2x
橘子 2.6 18﹣3.2x
合计 6 18
ii小王根据相等关系“苹果的单价×其质量=苹果购买金额”,得方程 .
单价(元/kg) 质量(kg) 金额(元)
苹果 3.2 x
橘子 2.6 6﹣x 2.6(6﹣x)
合计 6 18
iii小颖根据相等关系“橘子的单价×其质量=橘子购买金额”,得方程 .
单价(元/kg) 质量(kg) 金额(元)
苹果 3.2 x 3.2x
橘子 2.6 6﹣x
合计 6 18
(2)设苹果购买金额为y元,下列方程正确的是 .(填写正确的序号)
①; ②y+2.6(6)=18;
③3.2(6)=y; ④3.2(6)=18﹣y.
【分析】(1)根据“苹果质量+橘子质量=6kg,苹果单价×苹果质量=苹果购买金额和橘子的单价×其质量=橘子购买金额”填表、列出方程即可;
(2)分别根据“苹果质量+橘子质量=6kg和苹果单价×苹果质量=苹果购买金额”可得答案.
【解析】(1)①设小丽买了x千克的苹果,则她买橘子(6﹣x)千克.
由题意得:3.2x+2.6(6﹣x)=18;
故答案为:3.2x+2.6(6﹣x)=18;
②i补全表格如下:
单价(元/kg) 质量(kg) 金额(元)
苹果 3.2 x 3.2x
橘子 2.6 18﹣3.2x
合计 6 18
根据相等关系“所买苹果的质量+橘子的质量=6kg”,得方程:x+=6,
故答案为:x+=6;
ii补全表格如下:
单价(元/kg) 质量(kg) 金额(元)
苹果 3.2 x 18﹣2.6(6﹣x)
橘子 2.6 6﹣x 2.6(6﹣x)
合计 6 18
根据相等关系“苹果的单价×其质量=苹果购买金额”,得方程:3.2x=18﹣2.6(6﹣x),
故答案为:3.2x=18﹣2.6(6﹣x).
iii补全表格如下:
单价(元/kg) 质量(kg) 金额(元)
苹果 3.2 x 3.2x
橘子 2.6 6﹣x 18﹣3.2x
合计 6 18
根据相等关系“橘子的单价×其质量=橘子购买金额”,得方程:2.6(6﹣x)=18﹣3.2x,
故答案为:2.6(6﹣x)=18﹣3.2x.
(2)设苹果购买金额为y元,所列方程正确的是①③,
故答案为:①③.
