4.1 函数 同步练习卷 2021-2022学年北师大版数学八年级上册(Word版含答案)
文档属性
| 名称 | 4.1 函数 同步练习卷 2021-2022学年北师大版数学八年级上册(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 117.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-27 09:27:27 | ||
图片预览


文档简介
2021年北师大版数学八年级上册
4.1《函数》同步练习卷
一、选择题
1.下面说法中正确的是( )
A.两个变量间的关系只能用关系式表示
B.图象不能直观的表示两个变量间的数量关系
C.借助表格可以表示出因变量随自变量的变化情况
D.以上说法都不对
2.在圆的周长C=2πr中,常量与变量分别是( ).
A.2是常量,C、π、r是变量
B.2是常量,C、r是变量
C.C、2是常量,r是变量
D.2是常量,C、r是变量
3.下列四个关系式:(1)y=x;(2)y=x2;(3)y=x3;(4)|y|=x,其中y不是x的函数的是( )
A.(1) B.(2) C.(3) D.(4)
4.某科研小组在网上获取了声音在空气中传播的速度与空气温度关系的一些数据(如下表):
下列说法错误的是( )
A.在这个变化中,自变量是温度,因变量是声速
B.温度越高,声速越快
C.当空气温度为20℃时,声音5s可以传播1740m
D.当温度每升高10℃,声速增加6m/s
5.函数的自变量x的取值范围是( )
A.x>3 B.x≥3 C.x<3 D.x≤3
6.小军用50元钱去买单价是8元的笔记本,则他剩余的钱Q(元)与他买这种笔记本的本数x之间的关系是( )
A.Q=8x B.Q=8x﹣50 C.Q=50﹣8x D.Q=8x+50
7.甲、乙两地相距320 km,一货车从甲地出发以80 km/h的速度匀速向乙地行驶,则货车距离乙地的路程s(km)与时间t(h)之间的函数表达式是( )
A.s=320t B.s=80t C.s=320-80t D.s=320-4t
8.已知函数y=则当x=2时,函数y的值为( )
A.5 B.6 C.7 D.8
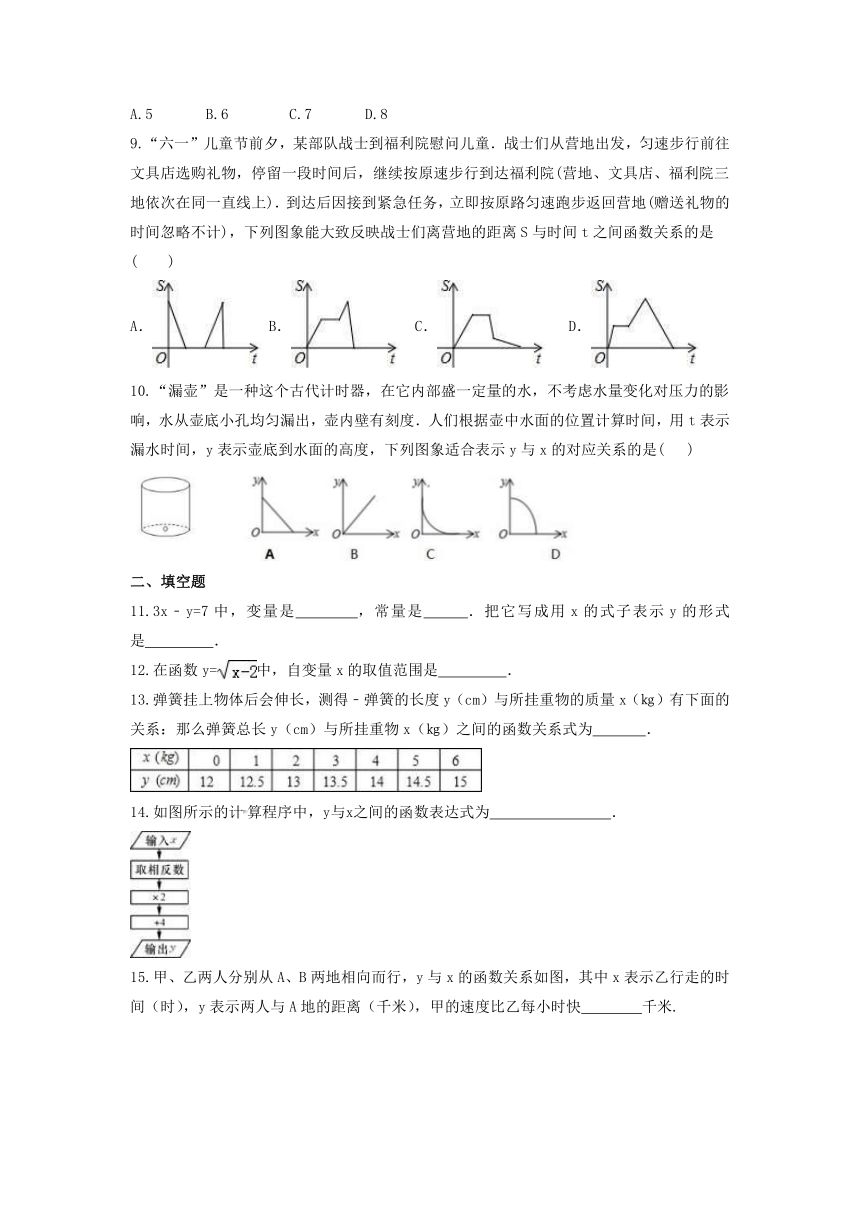
9.“六一”儿童节前夕,某部队战士到福利院慰问儿童.战士们从营地出发,匀速步行前往文具店选购礼物,停留一段时间后,继续按原速步行到达福利院(营地、文具店、福利院三地依次在同一直线上).到达后因接到紧急任务,立即按原路匀速跑步返回营地(赠送礼物的时间忽略不计),下列图象能大致反映战士们离营地的距离S与时间t之间函数关系的是( )
A. B. C. D.
10.“漏壶”是一种这个古代计时器,在它内部盛一定量的水,不考虑水量变化对压力的影响,水从壶底小孔均匀漏出,壶内壁有刻度.人们根据壶中水面的位置计算时间,用t表示漏水时间,y表示壶底到水面的高度,下列图象适合表示y与x的对应关系的是( )
二、填空题
11.3x﹣y=7中,变量是 ,常量是 .把它写成用x的式子表示y的形式是 .
12.在函数y=中,自变量x的取值范围是 .
13.弹簧挂上物体后会伸长,测得﹣弹簧的长度y(cm)与所挂重物的质量x(㎏)有下面的关系:那么弹簧总长y(cm)与所挂重物x(㎏)之间的函数关系式为 .
14.如图所示的计算程序中,y与x之间的函数表达式为 .
15.甲、乙两人分别从A、B两地相向而行,y与x的函数关系如图,其中x表示乙行走的时间(时),y表示两人与A地的距离(千米),甲的速度比乙每小时快 千米.
16.一慢车和一快车沿相同路线从A地到B地,所行的路程与时间图象如图,则慢车比快车早出发 小时,快车追上慢车行驶了 千米,快车比慢车早 小时到达B地.
三、解答题
17.某河受暴雨袭击,某天此河水的水位记录如下表:
(1)上表反映了哪两个变量之间的关系?
(2)12时,水位是多高?
(3)哪一时段水位上升最快?
18.父亲告诉小明:“距离地面越远,温度越低,”并给小明出示了下面的表格.
根据上表,父亲还给小明出了下面几个问题,你和小明一起回答.
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)如果用h表示距离地面的高度,用t表示温度,那么随着h的变化,t是怎么变化的?
(3)你知道距离地面6千米的高空温度是多少吗?
19.已知矩形周长为18,其中一条边长为x,设另一边长为y.
(1)写出y与x的函数关系式;
(2)求自变量x的取值范围.
20.在等腰三角形ABC中,AB=AC,△ABC的周长是20,底边BC的长为y,腰长为x.
(1)求y关于x的函数表达式.
(2)当腰AC=8时,求底边BC的长.
(3)当底边长为5时,求腰长.
21.王大爷带了若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价出售一些后,又降价出售,售出土豆的千克数x与他手中持有的钱数y(含备用零钱)的关系如图所示.根据图象回答下列问题:
(1)王大爷自带的零钱是多少?
(2)降价前他每千克土豆出售的价格是多少?
(3)降价后他按每千克0.4元将剩余土豆售完,这时他手中的钱(含备用零钱)是26元,问他一共带了多少千克土豆?
(4)写出售出土豆的千克数x与他手中持有的钱数y(含备用零钱)的关系式.
参考答案
1.答案为:C
2.答案为:B
3.答案为:D
4.答案为:C
5.答案为:D
6.答案为:C
7.答案为:C.
8.答案为:A.
9.答案为:B.
10.答案为:A.
11.答案是:x和y;3和7;y=3x﹣7.
12.答案为:x≥2.
13.答案为:y=0.5x+12.
14.答案为:y=-2x+4
15.答案为:0.4.
16.答案为:2,276,4.
17.解:(1)由表可知:反映了时间和水位之间的关系;
(2)由表可以看出:12时,水位是4米;
(3)由表可以看出:在相等的时间间隔内,20时至24时水位上升最快.
18.解:(1)上表反映了温度和距地面高度之间的关系,高度是自变量,温度是因变量.
(2)由表可知,每上升一千米,温度降低6 ℃,可得解析式为y=20-6x.
(3)由表可知,距地面5千米时,温度为零下10 ℃.
19.解:(1)∵矩形周长为18,其中一条边长为x,设另一边长为y,
∴2(x+y)=18,则y=9﹣x;
(2)由题意可得:9﹣x>0,解得:0<x<9.
20.解:(1)由题意,得2x+y=20,
∴y=-2x+20.
(2)AC=8,即x=8.
把x=8代入y=-2x+20,得
y=-2×8+20=4.
∴底边BC的长为4.
(3)底边长为5,即y=5.
把y=5代入y=-2x+20,得
-2x+20=5,解得x=7.5.
∴腰长为7.5.
21.解:(1)农民自带的零钱是5元;
(2)降价前每千克的土豆价格是:=0.5(元/千克);
(3)(26﹣20)÷0.4=15(千克),则一共带了30+15=45(千克).
(4)设降价出售前,农民手中的钱数与售出的土豆千克数的关系为:y=kx+b
把点(0,5),(30,20)代入可得:,解得:
则函数解析式是:y=x+5;设降价后的函数解析式是y=mx+n,
根据题意得:,解得:,则函数解析式是:y=0.4x+8.
4.1《函数》同步练习卷
一、选择题
1.下面说法中正确的是( )
A.两个变量间的关系只能用关系式表示
B.图象不能直观的表示两个变量间的数量关系
C.借助表格可以表示出因变量随自变量的变化情况
D.以上说法都不对
2.在圆的周长C=2πr中,常量与变量分别是( ).
A.2是常量,C、π、r是变量
B.2是常量,C、r是变量
C.C、2是常量,r是变量
D.2是常量,C、r是变量
3.下列四个关系式:(1)y=x;(2)y=x2;(3)y=x3;(4)|y|=x,其中y不是x的函数的是( )
A.(1) B.(2) C.(3) D.(4)
4.某科研小组在网上获取了声音在空气中传播的速度与空气温度关系的一些数据(如下表):
下列说法错误的是( )
A.在这个变化中,自变量是温度,因变量是声速
B.温度越高,声速越快
C.当空气温度为20℃时,声音5s可以传播1740m
D.当温度每升高10℃,声速增加6m/s
5.函数的自变量x的取值范围是( )
A.x>3 B.x≥3 C.x<3 D.x≤3
6.小军用50元钱去买单价是8元的笔记本,则他剩余的钱Q(元)与他买这种笔记本的本数x之间的关系是( )
A.Q=8x B.Q=8x﹣50 C.Q=50﹣8x D.Q=8x+50
7.甲、乙两地相距320 km,一货车从甲地出发以80 km/h的速度匀速向乙地行驶,则货车距离乙地的路程s(km)与时间t(h)之间的函数表达式是( )
A.s=320t B.s=80t C.s=320-80t D.s=320-4t
8.已知函数y=则当x=2时,函数y的值为( )
A.5 B.6 C.7 D.8
9.“六一”儿童节前夕,某部队战士到福利院慰问儿童.战士们从营地出发,匀速步行前往文具店选购礼物,停留一段时间后,继续按原速步行到达福利院(营地、文具店、福利院三地依次在同一直线上).到达后因接到紧急任务,立即按原路匀速跑步返回营地(赠送礼物的时间忽略不计),下列图象能大致反映战士们离营地的距离S与时间t之间函数关系的是( )
A. B. C. D.
10.“漏壶”是一种这个古代计时器,在它内部盛一定量的水,不考虑水量变化对压力的影响,水从壶底小孔均匀漏出,壶内壁有刻度.人们根据壶中水面的位置计算时间,用t表示漏水时间,y表示壶底到水面的高度,下列图象适合表示y与x的对应关系的是( )
二、填空题
11.3x﹣y=7中,变量是 ,常量是 .把它写成用x的式子表示y的形式是 .
12.在函数y=中,自变量x的取值范围是 .
13.弹簧挂上物体后会伸长,测得﹣弹簧的长度y(cm)与所挂重物的质量x(㎏)有下面的关系:那么弹簧总长y(cm)与所挂重物x(㎏)之间的函数关系式为 .
14.如图所示的计算程序中,y与x之间的函数表达式为 .
15.甲、乙两人分别从A、B两地相向而行,y与x的函数关系如图,其中x表示乙行走的时间(时),y表示两人与A地的距离(千米),甲的速度比乙每小时快 千米.
16.一慢车和一快车沿相同路线从A地到B地,所行的路程与时间图象如图,则慢车比快车早出发 小时,快车追上慢车行驶了 千米,快车比慢车早 小时到达B地.
三、解答题
17.某河受暴雨袭击,某天此河水的水位记录如下表:
(1)上表反映了哪两个变量之间的关系?
(2)12时,水位是多高?
(3)哪一时段水位上升最快?
18.父亲告诉小明:“距离地面越远,温度越低,”并给小明出示了下面的表格.
根据上表,父亲还给小明出了下面几个问题,你和小明一起回答.
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)如果用h表示距离地面的高度,用t表示温度,那么随着h的变化,t是怎么变化的?
(3)你知道距离地面6千米的高空温度是多少吗?
19.已知矩形周长为18,其中一条边长为x,设另一边长为y.
(1)写出y与x的函数关系式;
(2)求自变量x的取值范围.
20.在等腰三角形ABC中,AB=AC,△ABC的周长是20,底边BC的长为y,腰长为x.
(1)求y关于x的函数表达式.
(2)当腰AC=8时,求底边BC的长.
(3)当底边长为5时,求腰长.
21.王大爷带了若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价出售一些后,又降价出售,售出土豆的千克数x与他手中持有的钱数y(含备用零钱)的关系如图所示.根据图象回答下列问题:
(1)王大爷自带的零钱是多少?
(2)降价前他每千克土豆出售的价格是多少?
(3)降价后他按每千克0.4元将剩余土豆售完,这时他手中的钱(含备用零钱)是26元,问他一共带了多少千克土豆?
(4)写出售出土豆的千克数x与他手中持有的钱数y(含备用零钱)的关系式.
参考答案
1.答案为:C
2.答案为:B
3.答案为:D
4.答案为:C
5.答案为:D
6.答案为:C
7.答案为:C.
8.答案为:A.
9.答案为:B.
10.答案为:A.
11.答案是:x和y;3和7;y=3x﹣7.
12.答案为:x≥2.
13.答案为:y=0.5x+12.
14.答案为:y=-2x+4
15.答案为:0.4.
16.答案为:2,276,4.
17.解:(1)由表可知:反映了时间和水位之间的关系;
(2)由表可以看出:12时,水位是4米;
(3)由表可以看出:在相等的时间间隔内,20时至24时水位上升最快.
18.解:(1)上表反映了温度和距地面高度之间的关系,高度是自变量,温度是因变量.
(2)由表可知,每上升一千米,温度降低6 ℃,可得解析式为y=20-6x.
(3)由表可知,距地面5千米时,温度为零下10 ℃.
19.解:(1)∵矩形周长为18,其中一条边长为x,设另一边长为y,
∴2(x+y)=18,则y=9﹣x;
(2)由题意可得:9﹣x>0,解得:0<x<9.
20.解:(1)由题意,得2x+y=20,
∴y=-2x+20.
(2)AC=8,即x=8.
把x=8代入y=-2x+20,得
y=-2×8+20=4.
∴底边BC的长为4.
(3)底边长为5,即y=5.
把y=5代入y=-2x+20,得
-2x+20=5,解得x=7.5.
∴腰长为7.5.
21.解:(1)农民自带的零钱是5元;
(2)降价前每千克的土豆价格是:=0.5(元/千克);
(3)(26﹣20)÷0.4=15(千克),则一共带了30+15=45(千克).
(4)设降价出售前,农民手中的钱数与售出的土豆千克数的关系为:y=kx+b
把点(0,5),(30,20)代入可得:,解得:
则函数解析式是:y=x+5;设降价后的函数解析式是y=mx+n,
根据题意得:,解得:,则函数解析式是:y=0.4x+8.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
