青海省西宁市海湖中学2021-2022学年高二上学期第一次月考(10月)数学试题(PDF版含答案)
文档属性
| 名称 | 青海省西宁市海湖中学2021-2022学年高二上学期第一次月考(10月)数学试题(PDF版含答案) | 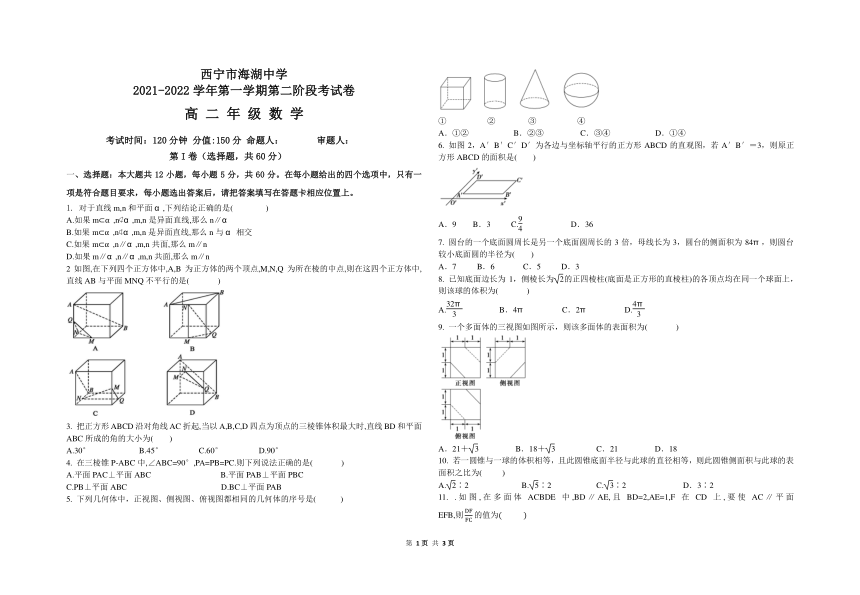 | |
| 格式 | zip | ||
| 文件大小 | 806.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-26 21:23:57 | ||
图片预览

文档简介
西宁市海湖中学
2021-2022 学年第一学期第二阶段考试卷
高 二 年 级 数 学
① ② ③ ④
A.①② B.②③ C.③④ D.①④
考试时间:120 分钟 分值:150 分 命题人: 审题人:
6. 如图 2,A′B′C′D′为各边与坐标轴平行的正方形 ABCD 的直观图,若 A′B′=3,则原正
第 I卷(选择题,共 60 分) 方形 ABCD 的面积是( )
一、选择题:本大题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一
项是符合题目要求,每小题选出答案后,请把答案填写在答题卡相应位置上。
1. 对于直线 m,n 和平面 α ,下列结论正确的是( )
A.如果 m α ,n α ,m,n 是异面直线,那么 n∥α 9
A.9 B.3 C. D.36
B.如果 m α ,n α 4,m,n 是异面直线,那么 n 与 α 相交
C.如果 m α ,n∥α ,m,n 共面,那么 m∥n 7. 圆台的一个底面圆周长是另一个底面圆周长的 3 倍,母线长为 3,圆台的侧面积为 84π ,则圆台
D.如果 m∥α ,n∥α ,m,n 共面,那么 m∥n 较小底面圆的半径为( )
2 如图,在下列四个正方体中,A,B 为正方体的两个顶点,M,N,Q 为所在棱的中点,则在这四个正方体中, A.7 B.6 C.5 D.3
直线 AB 与平面 MNQ 不平行的是( ) 8. 已知底面边长为 1,侧棱长为 2的正四棱柱(底面是正方形的直棱柱)的各顶点均在同一个球面上,
则该球的体积为( )
32π 4π
A. B.4π C.2π D.
3 3
9. 一个多面体的三视图如图所示,则该多面体的表面积为( )
3. 把正方形 ABCD 沿对角线 AC 折起,当以 A,B,C,D 四点为顶点的三棱锥体积最大时,直线 BD 和平面
ABC 所成的角的大小为( )
A.30° B.45° C.60° D.90° A.21+ 3 B.18+ 3 C.21 D.18
4. 在三棱锥 P-ABC 中,∠ABC=90°,PA=PB=PC.则下列说法正确的是( ) 10. 若一圆锥与一球的体积相等,且此圆锥底面半径与此球的直径相等,则此圆锥侧面积与此球的表
A.平面 PAC⊥平面 ABC B.平面 PAB⊥平面 PBC 面积之比为( )
C.PB⊥平面 ABC D.BC⊥平面 PAB A. 2∶2 B. 5∶2 C. 3∶2 D.3∶2
5. 下列几何体中,正视图、侧视图、俯视图都相同的几何体的序号是( ) 11. . 如图 , 在多面体 ACBDE 中 ,BD ∥ AE, 且 BD=2,AE=1,F 在 CD 上 , 要使 AC ∥平面
EFB,则 的值为
第 1 页 共 3页
三、解答题:本大题共 6小题,共 70分,解答应写出文字说明,证明过程或演算步骤。请在答
A.3 B.2 C.1 D
题卡各自题目的答题区域内作答。
12.. 已知一个正方体的展开图如图所示,其中A,B为所在棱的中点,C,D为原正方体的顶点,则在原来的
17. 如图 ,在三棱锥 P-ABC 中 ,平面 PAC⊥平面 ABC,∠ABC=90°,点 D,E 在线段 AC 上 ,且
正方体中 AB 与 CD 所成角的大小是( )
DE=EC,PD=PC,点 F 在线段 AB 上,且 EF∥BC.证明:AB⊥平面 PFE.
A.30° B.45° C.60° D.90°
第 II 卷(非选择题,共 90 分)
二、填空题 :本大题共 4小题,每小题 5分,共 20 分,请把答案填在答题卡的横线上。
18. 已知一个圆柱的侧面展开图是边长为 6π 和 8π 的矩形,求该圆柱的表面积.
13. .已知 a,b,c 是空间中的三条相互不重合的直线,给出下列说法:
①若 a∥b,b∥c,则 a∥c;
②若 a 与 b 相交,b 与 c 相交,则 a 与 c 相交;
③若 a 平面 α ,b 平面 β ,则 a,b 一定是异面直线;
④若 a,b 与 c 成等角,则 a∥b.
其中正确的是 .(只填序号)
14. 一个圆台上、下底面的半径分别为 3 cm 和 8 cm,若两底面圆心的连线长为 12 cm,则这个圆台 19. 如图,在 Rt△AOB 中,∠OAB=30°,斜边 AB=4,Rt△AOC 可以通过 Rt△AOB 以直线 AO 为轴旋转
的母线长为________cm. 得到,且平面 AOB⊥平面 AOC.动点 D 在斜边 AB 上.
15. 若各顶点都在一个球面上的长方体的高为 4,底面边长都为 2,则这个球的表面积是________.
16. .如图,PA⊥平面 ABC,∠ACB=90°,且 PA=AC=BC=a,则异面直线 PB 与 AC 所成角的正切值等于 (1)求证:平面 COD⊥平面 AOB;
________. (2)当 D 为 AB 的中点时,求异面直线 AO 与 CD 所成角的正切值.
第 2 页 共 3页
20. 如图 10 所示,正方体 ABCD A′B′C′D′的棱长为 a,连接 A′C′,A′D,A′B,BD, 22. 在三棱柱 ABC-A1B1C1中,侧棱垂直于底面,AB⊥BC,AA1=AC=2,BC=1,E,F 分别是 A1C1,BC 的中点.
BC′,C′D,得到一个三棱锥.求:
图 10 求证:C1F∥平面 ABE;
(1)三棱锥 A′ BC′D 的表面积与正方体表面积的比值;
(2)三棱锥 A′ BC′D 的体积.
21. )如图,在四棱锥 P-ABCD 中,PC⊥平面 ABCD,AB∥DC,DC⊥AC.
(1)求证:DC⊥平面 PAC.
(2)求证:平面 PAB⊥平面 PAC.
第 3 页 共 3页
2021-2022 学年第一学期第二阶段考试卷
高 二 年 级 数 学
① ② ③ ④
A.①② B.②③ C.③④ D.①④
考试时间:120 分钟 分值:150 分 命题人: 审题人:
6. 如图 2,A′B′C′D′为各边与坐标轴平行的正方形 ABCD 的直观图,若 A′B′=3,则原正
第 I卷(选择题,共 60 分) 方形 ABCD 的面积是( )
一、选择题:本大题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一
项是符合题目要求,每小题选出答案后,请把答案填写在答题卡相应位置上。
1. 对于直线 m,n 和平面 α ,下列结论正确的是( )
A.如果 m α ,n α ,m,n 是异面直线,那么 n∥α 9
A.9 B.3 C. D.36
B.如果 m α ,n α 4,m,n 是异面直线,那么 n 与 α 相交
C.如果 m α ,n∥α ,m,n 共面,那么 m∥n 7. 圆台的一个底面圆周长是另一个底面圆周长的 3 倍,母线长为 3,圆台的侧面积为 84π ,则圆台
D.如果 m∥α ,n∥α ,m,n 共面,那么 m∥n 较小底面圆的半径为( )
2 如图,在下列四个正方体中,A,B 为正方体的两个顶点,M,N,Q 为所在棱的中点,则在这四个正方体中, A.7 B.6 C.5 D.3
直线 AB 与平面 MNQ 不平行的是( ) 8. 已知底面边长为 1,侧棱长为 2的正四棱柱(底面是正方形的直棱柱)的各顶点均在同一个球面上,
则该球的体积为( )
32π 4π
A. B.4π C.2π D.
3 3
9. 一个多面体的三视图如图所示,则该多面体的表面积为( )
3. 把正方形 ABCD 沿对角线 AC 折起,当以 A,B,C,D 四点为顶点的三棱锥体积最大时,直线 BD 和平面
ABC 所成的角的大小为( )
A.30° B.45° C.60° D.90° A.21+ 3 B.18+ 3 C.21 D.18
4. 在三棱锥 P-ABC 中,∠ABC=90°,PA=PB=PC.则下列说法正确的是( ) 10. 若一圆锥与一球的体积相等,且此圆锥底面半径与此球的直径相等,则此圆锥侧面积与此球的表
A.平面 PAC⊥平面 ABC B.平面 PAB⊥平面 PBC 面积之比为( )
C.PB⊥平面 ABC D.BC⊥平面 PAB A. 2∶2 B. 5∶2 C. 3∶2 D.3∶2
5. 下列几何体中,正视图、侧视图、俯视图都相同的几何体的序号是( ) 11. . 如图 , 在多面体 ACBDE 中 ,BD ∥ AE, 且 BD=2,AE=1,F 在 CD 上 , 要使 AC ∥平面
EFB,则 的值为
第 1 页 共 3页
三、解答题:本大题共 6小题,共 70分,解答应写出文字说明,证明过程或演算步骤。请在答
A.3 B.2 C.1 D
题卡各自题目的答题区域内作答。
12.. 已知一个正方体的展开图如图所示,其中A,B为所在棱的中点,C,D为原正方体的顶点,则在原来的
17. 如图 ,在三棱锥 P-ABC 中 ,平面 PAC⊥平面 ABC,∠ABC=90°,点 D,E 在线段 AC 上 ,且
正方体中 AB 与 CD 所成角的大小是( )
DE=EC,PD=PC,点 F 在线段 AB 上,且 EF∥BC.证明:AB⊥平面 PFE.
A.30° B.45° C.60° D.90°
第 II 卷(非选择题,共 90 分)
二、填空题 :本大题共 4小题,每小题 5分,共 20 分,请把答案填在答题卡的横线上。
18. 已知一个圆柱的侧面展开图是边长为 6π 和 8π 的矩形,求该圆柱的表面积.
13. .已知 a,b,c 是空间中的三条相互不重合的直线,给出下列说法:
①若 a∥b,b∥c,则 a∥c;
②若 a 与 b 相交,b 与 c 相交,则 a 与 c 相交;
③若 a 平面 α ,b 平面 β ,则 a,b 一定是异面直线;
④若 a,b 与 c 成等角,则 a∥b.
其中正确的是 .(只填序号)
14. 一个圆台上、下底面的半径分别为 3 cm 和 8 cm,若两底面圆心的连线长为 12 cm,则这个圆台 19. 如图,在 Rt△AOB 中,∠OAB=30°,斜边 AB=4,Rt△AOC 可以通过 Rt△AOB 以直线 AO 为轴旋转
的母线长为________cm. 得到,且平面 AOB⊥平面 AOC.动点 D 在斜边 AB 上.
15. 若各顶点都在一个球面上的长方体的高为 4,底面边长都为 2,则这个球的表面积是________.
16. .如图,PA⊥平面 ABC,∠ACB=90°,且 PA=AC=BC=a,则异面直线 PB 与 AC 所成角的正切值等于 (1)求证:平面 COD⊥平面 AOB;
________. (2)当 D 为 AB 的中点时,求异面直线 AO 与 CD 所成角的正切值.
第 2 页 共 3页
20. 如图 10 所示,正方体 ABCD A′B′C′D′的棱长为 a,连接 A′C′,A′D,A′B,BD, 22. 在三棱柱 ABC-A1B1C1中,侧棱垂直于底面,AB⊥BC,AA1=AC=2,BC=1,E,F 分别是 A1C1,BC 的中点.
BC′,C′D,得到一个三棱锥.求:
图 10 求证:C1F∥平面 ABE;
(1)三棱锥 A′ BC′D 的表面积与正方体表面积的比值;
(2)三棱锥 A′ BC′D 的体积.
21. )如图,在四棱锥 P-ABCD 中,PC⊥平面 ABCD,AB∥DC,DC⊥AC.
(1)求证:DC⊥平面 PAC.
(2)求证:平面 PAB⊥平面 PAC.
第 3 页 共 3页
同课章节目录
