2021-2022学年北师大版九年级数学上册4.4探索三角形相似的条件 解答题专题训练(word版含答案)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学上册4.4探索三角形相似的条件 解答题专题训练(word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 288.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-27 10:30:58 | ||
图片预览


文档简介
2021-2022学年北师大版九年级数学上册《4.4探索三角形相似的条件》
解答题专题训练(附答案)
1.如图,AB⊥BD,CD⊥BD,AB=12,CD=8,BD=28,点P在BD上移动,当以P,C,D为顶点的三角形与△ABP相似时,求PB的长.
2.如图,已知∠BAC=∠EAD,AB=24,AC=48,AE=17,AD=34,求证:△ABC∽△AED.
3.如图,在Rt△ABC中,∠C=90°,AC=10cm,BC=8cm.点M从点C出发,以2cm/s的速度沿CA向点A匀速运动,点N从点B出发,以1cm/s的速度沿BC向点C匀速运动,当一个点到达终点时,另一点也随即停止运动.
(1)经过几秒后,△MCN的面积等于△ABC面积的?
(2)经过几秒,△MCN与△ABC相似?
4.如图,在△ABC中,四边形DBFE是平行四边形.求证:△ADE∽△EFC.
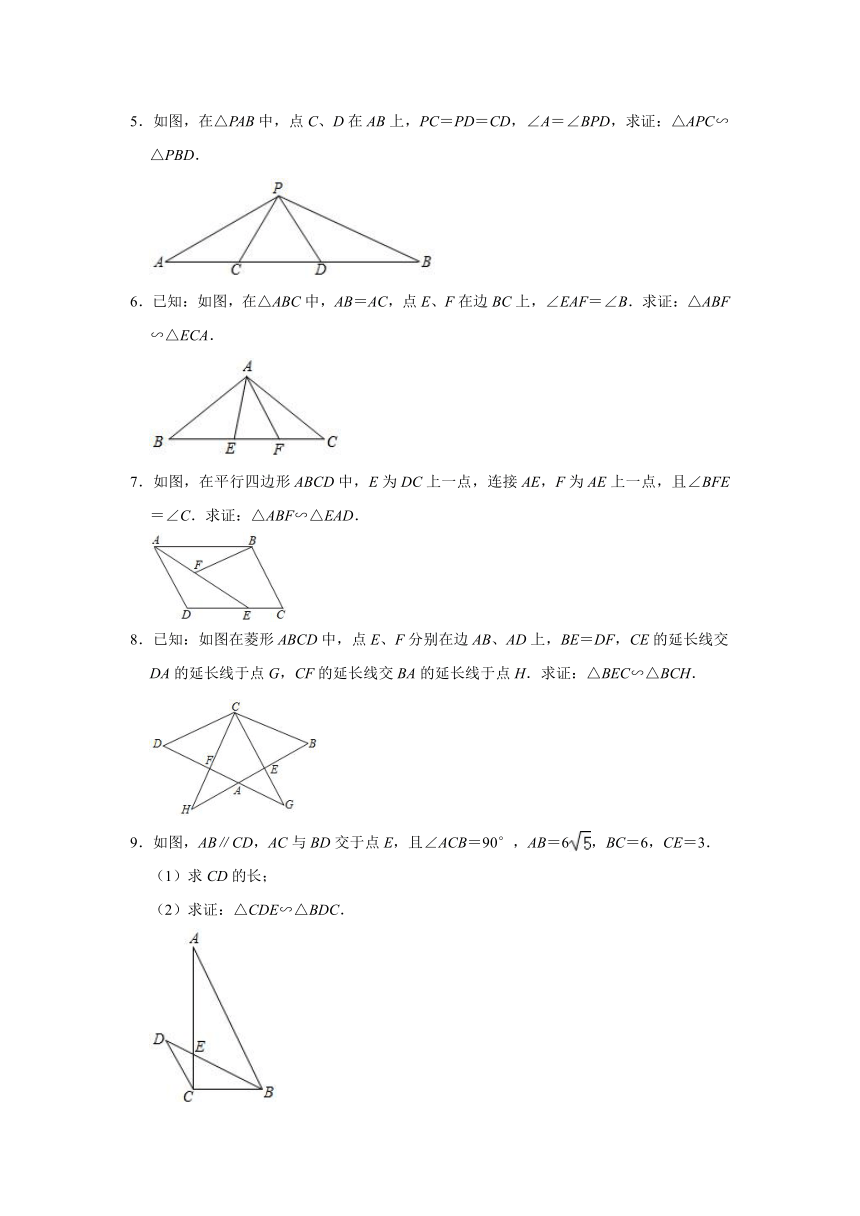
5.如图,在△PAB中,点C、D在AB上,PC=PD=CD,∠A=∠BPD,求证:△APC∽△PBD.
6.已知:如图,在△ABC中,AB=AC,点E、F在边BC上,∠EAF=∠B.求证:△ABF∽△ECA.
7.如图,在平行四边形ABCD中,E为DC上一点,连接AE,F为AE上一点,且∠BFE=∠C.求证:△ABF∽△EAD.
8.已知:如图在菱形ABCD中,点E、F分别在边AB、AD上,BE=DF,CE的延长线交DA的延长线于点G,CF的延长线交BA的延长线于点H.求证:△BEC∽△BCH.
9.如图,AB∥CD,AC与BD交于点E,且∠ACB=90°,AB=6,BC=6,CE=3.
(1)求CD的长;
(2)求证:△CDE∽△BDC.
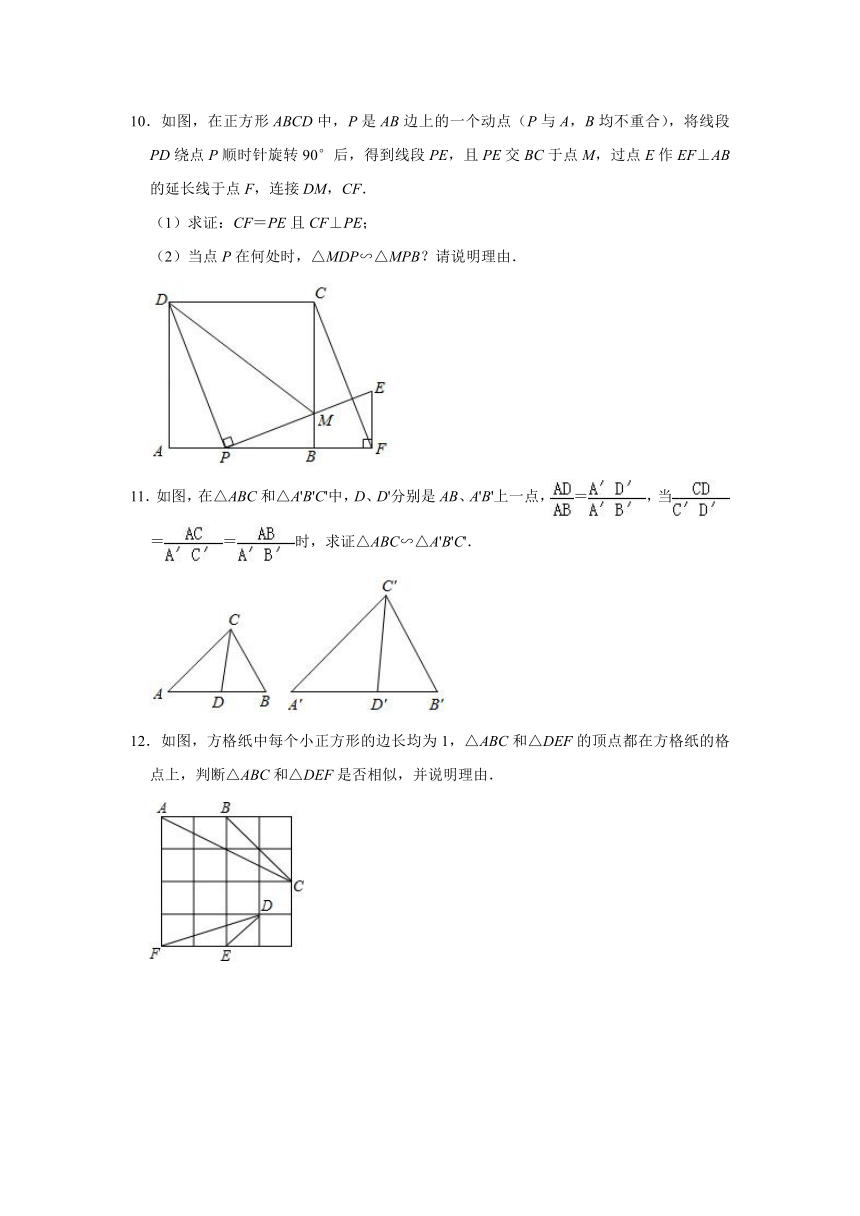
10.如图,在正方形ABCD中,P是AB边上的一个动点(P与A,B均不重合),将线段PD绕点P顺时针旋转90°后,得到线段PE,且PE交BC于点M,过点E作EF⊥AB的延长线于点F,连接DM,CF.
(1)求证:CF=PE且CF⊥PE;
(2)当点P在何处时,△MDP∽△MPB?请说明理由.
11.如图,在△ABC和△A'B'C'中,D、D'分别是AB、A'B'上一点,=,当==时,求证△ABC∽△A'B'C'.
12.如图,方格纸中每个小正方形的边长均为1,△ABC和△DEF的顶点都在方格纸的格点上,判断△ABC和△DEF是否相似,并说明理由.
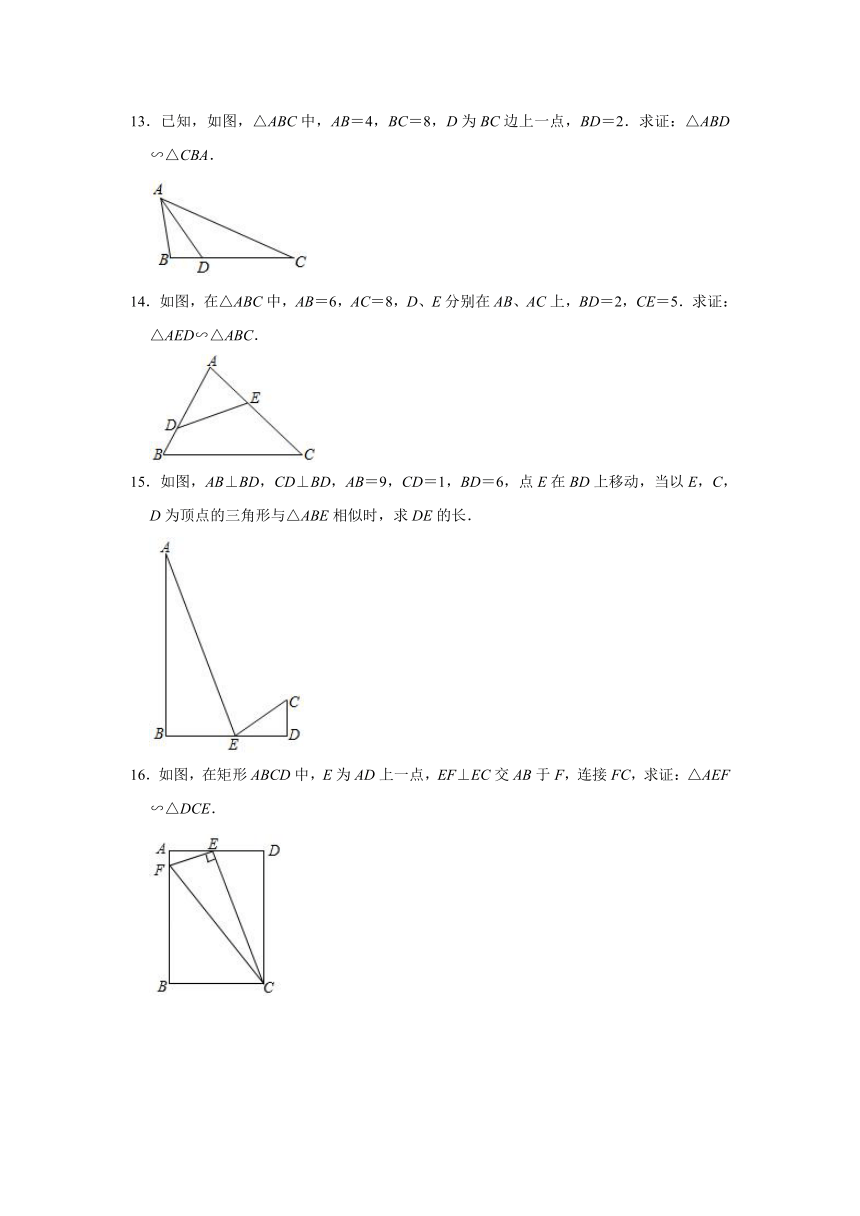
13.已知,如图,△ABC中,AB=4,BC=8,D为BC边上一点,BD=2.求证:△ABD∽△CBA.
14.如图,在△ABC中,AB=6,AC=8,D、E分别在AB、AC上,BD=2,CE=5.求证:△AED∽△ABC.
15.如图,AB⊥BD,CD⊥BD,AB=9,CD=1,BD=6,点E在BD上移动,当以E,C,D为顶点的三角形与△ABE相似时,求DE的长.
16.如图,在矩形ABCD中,E为AD上一点,EF⊥EC交AB于F,连接FC,求证:△AEF∽△DCE.
17.如图,在△ABC中,∠C=90°,AC=6cm,BC=8cm,点P从点A出发沿边AC向点C以1cm/s的速度移动,点Q从点C出发沿CB边向点B以2cm/s的速度移动,当其中一点到达终点时,另一点也随之停止运动.
(1)如果点P,Q同时出发,经过几秒钟时△PCQ的面积为8cm2?
(2)如果点P,Q同时出发,经过几秒钟时以P、C、Q为顶点的三角形与△ABC相似?
18.如图,△ABC中,BD⊥AC于D,CE⊥AB于E,设BD与CE相交于F点.
(1)求证:△BEF∽△CDF;
(2)求证:DE BF=EF BC.
19.已知:如图,点C,D在线段AB上,△PCD是等边三角形,且AC=1,CD=2,DB=4.求证:△ACP∽△PDB.
20.如图,AB AE=AD AC,且∠1=∠2,求证:△ABC∽△ADE.
21.已知如图,D、E分别是△ABC的边AB,AC上的点,AD=5,AB=8,AE=4,AC=10.求证:△ADE∽△ACB.
22.如图,在正方形ABCD中,点E在AD上,EF⊥BE交CD于点F.
(1)求证:△ABE∽△DEF;
(2)连接BF,若△ABE∽△EBF,试确定点E的位置并说明理由.
23.如图,BD、AC相交于点P,连接BC、AD,且∠1=∠2,求证:△ADP∽△BCP.
24.阅读下面材料:
小军遇到这样一个问题:如图1,在△ABC中,AB=AC,P是△ABC内一点,
∠PAC=∠PCB=∠PBA.若∠ACB=45°,AP=1,求BP的长.
小军的思路是:根据已知条件可以证明△ACP∽△CBP,进一步推理可得BP的长.
请回答:∵AB=AC,
∴∠ABC=∠ACB.
∵∠PCB=∠PBA,
∴∠PCA= .
∵∠PAC=∠PCB,
∴△ACP∽△CBP.
∴.
∵∠ACB=45°,
∴∠BAC=90°.
∴= .
∵AP=1,
∴PC=.
∴PB= .
参考小军的思路,解决问题:
如图2,在△ABC中,AB=AC,P是△ABC内一点,∠PAC=∠PCB=∠PBA.若∠ACB=30°,求的值;
25.如图,点B、D、E在一条直线上,BE交AC于点F,=,且∠BAD=∠CAE.
(1)求证:△ABC∽△ADE;
(2)求证:△AEF∽△BCF.
参考答案
1.解:设DP=x,则BP=BD﹣x=14﹣x,
∵AB⊥BD于B,CD⊥BD于D,
∴∠B=∠D=90°,
∴当=时,△ABP∽△CDP,即=,
解得x=,
经检验x=是分式方程的解,
BP=28﹣=16.8;
当=时,△ABP∽△PDC,即=,
解得x1=4,x2=24,
经检验,x=4或24是分式方程的解,
BP=28﹣4=24,BP=28﹣24=4,
∴当BP为16.8或4或24时,以C、D、P为顶点的三角形与以P、B、A为顶点的三角形相似.
2.证明:∵AB=24,AC=48,AE=17,AD=34,
∴==,
∴=,
∵∠BAC=∠EAD,
∴△BAC∽△EAD.
3.解:(1)设经过x秒,△MCN的面积等于△ABC面积的.
×2x(8﹣x)=×8×10×.
解得x1=x2=4.
答:经过4秒后,△MCN的面积等于△ABC面积的;
(2)设经过t秒,△MCN与△ABC相似.
∵∠C=∠C,
∴可分为两种情况:
①=,即=,
解得t=;
②=,即=.
解得t=.
答:经过或秒,△MCN与△ABC相似.
4.证明:∵四边形DBFE是平行四边形,
∴DE∥BC,EF∥AB,
∴∠CEF=∠A,∠AED=∠C,
∴△ADE∽△EFC.
5.证明:∵PC=PD,
∴∠PCD=∠PDC,
∵∠A+∠APC=∠PCD,∠B+∠BPD=∠PDC,
又∵∠A=∠BPD,
∴∠B=∠APC,
∴△APC∽△PBD.
6.证明:∵∠AEC=∠B+∠BAE,∠BAF=∠EAF+∠BAE,∠EAF=∠B,
∴∠AEC=∠BAF,
又∵AB=AC,
∴∠B=∠C,
∴△ABF∽△ECA.
7.证明:∵四边形ABCD是平行四边形,
∴∠BAF=∠AED,且∠C+∠D=180°,
又∵∠BFE+∠BFA=180°,
∵∠BFE=∠C,
∴∠BFA=∠D,
∴△ABF∽△EAD.
8.证明:∵四边形ABCD是菱形,
∴CD=CB,∠D=∠B,
∵DF=BE,
∴△CDF≌△CBE(SAS),
∴∠DCF=∠BCE,
∵CD∥BH,
∴∠H=∠DCF,
∴∠H=∠BCE,
∵∠B=∠B,
∴△BEC∽△BCH.
9.(1)解:∵∠ACB=90°AB=6,BC=6,
∴AC==12;
∴AE=AC﹣CE=9,
∵AB∥CD,
∴△CDE∽△ABE;
∴,
∴CD===2,
(2)证明:∵∠ACB=90°,CE=3,BC=6,
∴BE==3,
∵AB∥CD,
∴△CDE∽△ABE,
∴,
∴DE=,
∴BD=4,
∵,,
∴,
∵∠D=∠D,
∴△CDE∽△BDC.
10.解:(1)证明:在正方形ABCD中,P在边AB上,且∠DPE=∠A=90°,
∴∠APD+∠ADP=∠APD+∠FPE=90°,
∴∠ADP=∠FPE,
∵EF⊥AB,
∴∠PFE=∠A=90°,
在△PEF和△DPA中,
,
∴△PEF≌△DPA(AAS),
∴PF=AD=AB=DC,
又AF∥CD,
∴四边形PFCD是平行四边形,
∴CF=PD=PE,CF∥PD,
∵DP⊥PE,
∴CF⊥PE.
(2)当点P是AB的中点时,△MDP∽△MPB.
理由:∵△MDP∽△MPB,
∴,
∵∠ADP=∠BPM,∠A=∠PBM,
∴△PDA∽△MPB,
∴,
∴,
∴PA=PB,
即点P是边AB的中点,
∴当点P恰好是AB边的中点时,△MDP∽△MPB.
11.证明:∵,
∴,
∵,
∴,
∴△ADC∽△A'D'C',
∴∠A=∠A',
∵,
∴△ABC∽△A'B'C.
12.解:△ABC和△DEF相似;
理由如下:由图形可知AB=2,根据勾股定理得,BC=2,AC=2;DE=,DF=,EF=2,
∵,
∴△ABC∽△DEF.
13.证明:∵AB=4,BC=8,BD=2,
∴.
∵∠ABD=∠CBA,
∴△ABD∽△CBA.
14.证明:∵AB=6,BD=2,
∴AD=4,
∵AC=8,CE=5,
∴AE=3,
∴,,
∴,
∵∠EAD=∠BAC,
∴△AED∽△ABC.
15.解:设DE=x,则BE=BD﹣x=6﹣x,
∵AB⊥BD于B,CD⊥BD于D,
∴∠B=∠D=90°,
∴当时,△ABE∽△CDE,即,
解得x=,
当时,△ABE∽△EDC,即,
整理得x2﹣6x+9=0,
解得x1=x2=3,
∴当DE为或3时,以C、D、E为顶点的三角形与以E、B、A为顶点的三角形相似.
16.证明:∵∠FEC=90°,
∴∠AEF+∠DEC=90°,
∵四边形ABCD是矩形,
∴∠A=∠D=90°,
∵∠A+∠AFE+∠AEF=180°,
∴∠AFE+∠AEF=90°,
∴∠DEC=∠AFE,
又∵∠A=∠D,
∴△AEF∽△DCE.
17.解:(1)设xs后,可使△PCQ的面积为8cm2.
由题意得,AP=xcm,PC=(6﹣x)cm,CQ=2xcm,
则(6﹣x) 2x=8,
整理得x2﹣6x+8=0,
解得x1=2,x2=4.
所以P、Q同时出发,2s或4s后可使△PCQ的面积为8cm2.
(2)设t秒后以P、C、Q为顶点的三角形与△ABC相似,则PC=(6﹣t)cm,CQ=2tcm.
当△PCQ∽△ACB时,=,即=,
解得:t=.
当△PCQ∽△BCA时,=,即=,
解得:t=.
综上所述,经过秒或秒时,以P、C、Q为顶点的三角形与△ABC相似.
18.证明:(1)∵BD⊥AC,CE⊥AB,
∴∠BEF=∠CDF=90°,且∠EFB=∠DFC,
∴△BEF∽△CDF;
(2)如图,连接DE,
∵∠BEF=∠CDF=90°,
∴点B,点C,点D,点E四点共圆,
∴∠DEF=∠DBC,∠BFC=∠DFE,
∴△DEF∽△CBF,
∴,
∴DE BF=EF BC
19.证明:∵△PCD是等边三角形,
∴∠PCD=∠PDC=60°,PC=CD=PD=2,
∴∠PCA=∠PDB=120°,
∵AC=1,BD=4,
∴,=,
∴=,
∴△ACP∽△PDB.
20.证明:如图,∵AB AE=AD AC,
∴=.
又∵∠1=∠2,
∴∠2+∠BAE=∠1+∠BAE,即∠BAC=∠DAE,
∴△ABC∽△ADE.
21.证明:∵AD=5,AB=8,AE=4,AC=10,
∴,
又∵∠DAE=∠CAB,
∴△ADE∽△ACB.
22.(1)证明∵四边形ABCD是正方形,
∴∠A=∠D=90°.
∴∠AEB+∠ABE=90°.
∵EF⊥BE,
∴∠AEB+∠DEF=90°.
∴∠ABE=∠DEF.
在△ABE和△DEF中,∠ABE=∠DEF,∠A=∠D,
∴△ABE∽△DEF;
(2)解:点E为AD的中点时,△ABE∽△EBF,理由如下:
∵△ABE∽△DEF,
∴.
∵△ABE∽△EBF,
∴.
∴.
∴DE=AE.
∴点E为AD的中点.
23.证明:∵∠1=∠2,∠DPA=∠CPB,
∴△ADP∽△BCP.
24.阅读材料:
解:∵AB=AC,
∴∠ABC=∠ACB.
∵∠PCB=∠PBA,
∴∠PCA=∠PBC.
∵∠PAC=∠PCB,
∴△ACP∽△CBP.
∴.
∵∠ACB=45°,
∴∠BAC=90°.
∴CB=AC,
∴=.
∵AP=1,
∴PC=AP=.
∴PB=PC=2.
故答案为:∠PBC;;2;
解决问题:
解:过点A作AD⊥BC于D,如图2所示:
∵AB=AC,
∴∠ABC=∠ACB=30°.BD=CD=BC,
∴AD=AC,CD=AD,
∴AC=2AD,BC=2CD=2AD,
∵∠PCB=∠PBA,
∴∠PCA=∠PBC.
∵∠PAC=∠PCB,
∴△ACP∽△CBP.
∴==,
设AP=a,则PC=,
∴PB=3a.
∴.
25.(1)∵∠BAD=∠CAE
∴∠BAD+∠CAD=∠CAE+∠CAD
即∠BAC=∠DAE
在△ABC和△ADE中
=,∠BAC=∠DAE,
∴△ABC∽△ADE;
(2)∵△ABC∽△ADE,
∴∠C=∠E、
在△AEF和△BFC中,∠C=∠E,∠AFE=∠BFC,
∴△AEF∽△BCF.
解答题专题训练(附答案)
1.如图,AB⊥BD,CD⊥BD,AB=12,CD=8,BD=28,点P在BD上移动,当以P,C,D为顶点的三角形与△ABP相似时,求PB的长.
2.如图,已知∠BAC=∠EAD,AB=24,AC=48,AE=17,AD=34,求证:△ABC∽△AED.
3.如图,在Rt△ABC中,∠C=90°,AC=10cm,BC=8cm.点M从点C出发,以2cm/s的速度沿CA向点A匀速运动,点N从点B出发,以1cm/s的速度沿BC向点C匀速运动,当一个点到达终点时,另一点也随即停止运动.
(1)经过几秒后,△MCN的面积等于△ABC面积的?
(2)经过几秒,△MCN与△ABC相似?
4.如图,在△ABC中,四边形DBFE是平行四边形.求证:△ADE∽△EFC.
5.如图,在△PAB中,点C、D在AB上,PC=PD=CD,∠A=∠BPD,求证:△APC∽△PBD.
6.已知:如图,在△ABC中,AB=AC,点E、F在边BC上,∠EAF=∠B.求证:△ABF∽△ECA.
7.如图,在平行四边形ABCD中,E为DC上一点,连接AE,F为AE上一点,且∠BFE=∠C.求证:△ABF∽△EAD.
8.已知:如图在菱形ABCD中,点E、F分别在边AB、AD上,BE=DF,CE的延长线交DA的延长线于点G,CF的延长线交BA的延长线于点H.求证:△BEC∽△BCH.
9.如图,AB∥CD,AC与BD交于点E,且∠ACB=90°,AB=6,BC=6,CE=3.
(1)求CD的长;
(2)求证:△CDE∽△BDC.
10.如图,在正方形ABCD中,P是AB边上的一个动点(P与A,B均不重合),将线段PD绕点P顺时针旋转90°后,得到线段PE,且PE交BC于点M,过点E作EF⊥AB的延长线于点F,连接DM,CF.
(1)求证:CF=PE且CF⊥PE;
(2)当点P在何处时,△MDP∽△MPB?请说明理由.
11.如图,在△ABC和△A'B'C'中,D、D'分别是AB、A'B'上一点,=,当==时,求证△ABC∽△A'B'C'.
12.如图,方格纸中每个小正方形的边长均为1,△ABC和△DEF的顶点都在方格纸的格点上,判断△ABC和△DEF是否相似,并说明理由.
13.已知,如图,△ABC中,AB=4,BC=8,D为BC边上一点,BD=2.求证:△ABD∽△CBA.
14.如图,在△ABC中,AB=6,AC=8,D、E分别在AB、AC上,BD=2,CE=5.求证:△AED∽△ABC.
15.如图,AB⊥BD,CD⊥BD,AB=9,CD=1,BD=6,点E在BD上移动,当以E,C,D为顶点的三角形与△ABE相似时,求DE的长.
16.如图,在矩形ABCD中,E为AD上一点,EF⊥EC交AB于F,连接FC,求证:△AEF∽△DCE.
17.如图,在△ABC中,∠C=90°,AC=6cm,BC=8cm,点P从点A出发沿边AC向点C以1cm/s的速度移动,点Q从点C出发沿CB边向点B以2cm/s的速度移动,当其中一点到达终点时,另一点也随之停止运动.
(1)如果点P,Q同时出发,经过几秒钟时△PCQ的面积为8cm2?
(2)如果点P,Q同时出发,经过几秒钟时以P、C、Q为顶点的三角形与△ABC相似?
18.如图,△ABC中,BD⊥AC于D,CE⊥AB于E,设BD与CE相交于F点.
(1)求证:△BEF∽△CDF;
(2)求证:DE BF=EF BC.
19.已知:如图,点C,D在线段AB上,△PCD是等边三角形,且AC=1,CD=2,DB=4.求证:△ACP∽△PDB.
20.如图,AB AE=AD AC,且∠1=∠2,求证:△ABC∽△ADE.
21.已知如图,D、E分别是△ABC的边AB,AC上的点,AD=5,AB=8,AE=4,AC=10.求证:△ADE∽△ACB.
22.如图,在正方形ABCD中,点E在AD上,EF⊥BE交CD于点F.
(1)求证:△ABE∽△DEF;
(2)连接BF,若△ABE∽△EBF,试确定点E的位置并说明理由.
23.如图,BD、AC相交于点P,连接BC、AD,且∠1=∠2,求证:△ADP∽△BCP.
24.阅读下面材料:
小军遇到这样一个问题:如图1,在△ABC中,AB=AC,P是△ABC内一点,
∠PAC=∠PCB=∠PBA.若∠ACB=45°,AP=1,求BP的长.
小军的思路是:根据已知条件可以证明△ACP∽△CBP,进一步推理可得BP的长.
请回答:∵AB=AC,
∴∠ABC=∠ACB.
∵∠PCB=∠PBA,
∴∠PCA= .
∵∠PAC=∠PCB,
∴△ACP∽△CBP.
∴.
∵∠ACB=45°,
∴∠BAC=90°.
∴= .
∵AP=1,
∴PC=.
∴PB= .
参考小军的思路,解决问题:
如图2,在△ABC中,AB=AC,P是△ABC内一点,∠PAC=∠PCB=∠PBA.若∠ACB=30°,求的值;
25.如图,点B、D、E在一条直线上,BE交AC于点F,=,且∠BAD=∠CAE.
(1)求证:△ABC∽△ADE;
(2)求证:△AEF∽△BCF.
参考答案
1.解:设DP=x,则BP=BD﹣x=14﹣x,
∵AB⊥BD于B,CD⊥BD于D,
∴∠B=∠D=90°,
∴当=时,△ABP∽△CDP,即=,
解得x=,
经检验x=是分式方程的解,
BP=28﹣=16.8;
当=时,△ABP∽△PDC,即=,
解得x1=4,x2=24,
经检验,x=4或24是分式方程的解,
BP=28﹣4=24,BP=28﹣24=4,
∴当BP为16.8或4或24时,以C、D、P为顶点的三角形与以P、B、A为顶点的三角形相似.
2.证明:∵AB=24,AC=48,AE=17,AD=34,
∴==,
∴=,
∵∠BAC=∠EAD,
∴△BAC∽△EAD.
3.解:(1)设经过x秒,△MCN的面积等于△ABC面积的.
×2x(8﹣x)=×8×10×.
解得x1=x2=4.
答:经过4秒后,△MCN的面积等于△ABC面积的;
(2)设经过t秒,△MCN与△ABC相似.
∵∠C=∠C,
∴可分为两种情况:
①=,即=,
解得t=;
②=,即=.
解得t=.
答:经过或秒,△MCN与△ABC相似.
4.证明:∵四边形DBFE是平行四边形,
∴DE∥BC,EF∥AB,
∴∠CEF=∠A,∠AED=∠C,
∴△ADE∽△EFC.
5.证明:∵PC=PD,
∴∠PCD=∠PDC,
∵∠A+∠APC=∠PCD,∠B+∠BPD=∠PDC,
又∵∠A=∠BPD,
∴∠B=∠APC,
∴△APC∽△PBD.
6.证明:∵∠AEC=∠B+∠BAE,∠BAF=∠EAF+∠BAE,∠EAF=∠B,
∴∠AEC=∠BAF,
又∵AB=AC,
∴∠B=∠C,
∴△ABF∽△ECA.
7.证明:∵四边形ABCD是平行四边形,
∴∠BAF=∠AED,且∠C+∠D=180°,
又∵∠BFE+∠BFA=180°,
∵∠BFE=∠C,
∴∠BFA=∠D,
∴△ABF∽△EAD.
8.证明:∵四边形ABCD是菱形,
∴CD=CB,∠D=∠B,
∵DF=BE,
∴△CDF≌△CBE(SAS),
∴∠DCF=∠BCE,
∵CD∥BH,
∴∠H=∠DCF,
∴∠H=∠BCE,
∵∠B=∠B,
∴△BEC∽△BCH.
9.(1)解:∵∠ACB=90°AB=6,BC=6,
∴AC==12;
∴AE=AC﹣CE=9,
∵AB∥CD,
∴△CDE∽△ABE;
∴,
∴CD===2,
(2)证明:∵∠ACB=90°,CE=3,BC=6,
∴BE==3,
∵AB∥CD,
∴△CDE∽△ABE,
∴,
∴DE=,
∴BD=4,
∵,,
∴,
∵∠D=∠D,
∴△CDE∽△BDC.
10.解:(1)证明:在正方形ABCD中,P在边AB上,且∠DPE=∠A=90°,
∴∠APD+∠ADP=∠APD+∠FPE=90°,
∴∠ADP=∠FPE,
∵EF⊥AB,
∴∠PFE=∠A=90°,
在△PEF和△DPA中,
,
∴△PEF≌△DPA(AAS),
∴PF=AD=AB=DC,
又AF∥CD,
∴四边形PFCD是平行四边形,
∴CF=PD=PE,CF∥PD,
∵DP⊥PE,
∴CF⊥PE.
(2)当点P是AB的中点时,△MDP∽△MPB.
理由:∵△MDP∽△MPB,
∴,
∵∠ADP=∠BPM,∠A=∠PBM,
∴△PDA∽△MPB,
∴,
∴,
∴PA=PB,
即点P是边AB的中点,
∴当点P恰好是AB边的中点时,△MDP∽△MPB.
11.证明:∵,
∴,
∵,
∴,
∴△ADC∽△A'D'C',
∴∠A=∠A',
∵,
∴△ABC∽△A'B'C.
12.解:△ABC和△DEF相似;
理由如下:由图形可知AB=2,根据勾股定理得,BC=2,AC=2;DE=,DF=,EF=2,
∵,
∴△ABC∽△DEF.
13.证明:∵AB=4,BC=8,BD=2,
∴.
∵∠ABD=∠CBA,
∴△ABD∽△CBA.
14.证明:∵AB=6,BD=2,
∴AD=4,
∵AC=8,CE=5,
∴AE=3,
∴,,
∴,
∵∠EAD=∠BAC,
∴△AED∽△ABC.
15.解:设DE=x,则BE=BD﹣x=6﹣x,
∵AB⊥BD于B,CD⊥BD于D,
∴∠B=∠D=90°,
∴当时,△ABE∽△CDE,即,
解得x=,
当时,△ABE∽△EDC,即,
整理得x2﹣6x+9=0,
解得x1=x2=3,
∴当DE为或3时,以C、D、E为顶点的三角形与以E、B、A为顶点的三角形相似.
16.证明:∵∠FEC=90°,
∴∠AEF+∠DEC=90°,
∵四边形ABCD是矩形,
∴∠A=∠D=90°,
∵∠A+∠AFE+∠AEF=180°,
∴∠AFE+∠AEF=90°,
∴∠DEC=∠AFE,
又∵∠A=∠D,
∴△AEF∽△DCE.
17.解:(1)设xs后,可使△PCQ的面积为8cm2.
由题意得,AP=xcm,PC=(6﹣x)cm,CQ=2xcm,
则(6﹣x) 2x=8,
整理得x2﹣6x+8=0,
解得x1=2,x2=4.
所以P、Q同时出发,2s或4s后可使△PCQ的面积为8cm2.
(2)设t秒后以P、C、Q为顶点的三角形与△ABC相似,则PC=(6﹣t)cm,CQ=2tcm.
当△PCQ∽△ACB时,=,即=,
解得:t=.
当△PCQ∽△BCA时,=,即=,
解得:t=.
综上所述,经过秒或秒时,以P、C、Q为顶点的三角形与△ABC相似.
18.证明:(1)∵BD⊥AC,CE⊥AB,
∴∠BEF=∠CDF=90°,且∠EFB=∠DFC,
∴△BEF∽△CDF;
(2)如图,连接DE,
∵∠BEF=∠CDF=90°,
∴点B,点C,点D,点E四点共圆,
∴∠DEF=∠DBC,∠BFC=∠DFE,
∴△DEF∽△CBF,
∴,
∴DE BF=EF BC
19.证明:∵△PCD是等边三角形,
∴∠PCD=∠PDC=60°,PC=CD=PD=2,
∴∠PCA=∠PDB=120°,
∵AC=1,BD=4,
∴,=,
∴=,
∴△ACP∽△PDB.
20.证明:如图,∵AB AE=AD AC,
∴=.
又∵∠1=∠2,
∴∠2+∠BAE=∠1+∠BAE,即∠BAC=∠DAE,
∴△ABC∽△ADE.
21.证明:∵AD=5,AB=8,AE=4,AC=10,
∴,
又∵∠DAE=∠CAB,
∴△ADE∽△ACB.
22.(1)证明∵四边形ABCD是正方形,
∴∠A=∠D=90°.
∴∠AEB+∠ABE=90°.
∵EF⊥BE,
∴∠AEB+∠DEF=90°.
∴∠ABE=∠DEF.
在△ABE和△DEF中,∠ABE=∠DEF,∠A=∠D,
∴△ABE∽△DEF;
(2)解:点E为AD的中点时,△ABE∽△EBF,理由如下:
∵△ABE∽△DEF,
∴.
∵△ABE∽△EBF,
∴.
∴.
∴DE=AE.
∴点E为AD的中点.
23.证明:∵∠1=∠2,∠DPA=∠CPB,
∴△ADP∽△BCP.
24.阅读材料:
解:∵AB=AC,
∴∠ABC=∠ACB.
∵∠PCB=∠PBA,
∴∠PCA=∠PBC.
∵∠PAC=∠PCB,
∴△ACP∽△CBP.
∴.
∵∠ACB=45°,
∴∠BAC=90°.
∴CB=AC,
∴=.
∵AP=1,
∴PC=AP=.
∴PB=PC=2.
故答案为:∠PBC;;2;
解决问题:
解:过点A作AD⊥BC于D,如图2所示:
∵AB=AC,
∴∠ABC=∠ACB=30°.BD=CD=BC,
∴AD=AC,CD=AD,
∴AC=2AD,BC=2CD=2AD,
∵∠PCB=∠PBA,
∴∠PCA=∠PBC.
∵∠PAC=∠PCB,
∴△ACP∽△CBP.
∴==,
设AP=a,则PC=,
∴PB=3a.
∴.
25.(1)∵∠BAD=∠CAE
∴∠BAD+∠CAD=∠CAE+∠CAD
即∠BAC=∠DAE
在△ABC和△ADE中
=,∠BAC=∠DAE,
∴△ABC∽△ADE;
(2)∵△ABC∽△ADE,
∴∠C=∠E、
在△AEF和△BFC中,∠C=∠E,∠AFE=∠BFC,
∴△AEF∽△BCF.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
