2018-2019学年湖南省郴州市安仁县八年级(上)期中数学试卷(Word版 含解析)
文档属性
| 名称 | 2018-2019学年湖南省郴州市安仁县八年级(上)期中数学试卷(Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 322.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-27 08:14:16 | ||
图片预览




文档简介
2018-2019学年湖南省郴州市安仁县八年级(上)期中数学试卷
一、选择题(共9小题,每小题3分,满分27分)
1.(3分)下列各式:,,,,(x﹣y)中,是分式的共有( )
A.1个 B.2个 C.3个 D.4个
2.(3分)已知三角形的三边长分别为4,5,x,则x不可能是( )
A.3 B.5 C.7 D.9
3.(3分)若分式的值为零,则x等于( )
A.0 B.2 C.±2 D.﹣2
4.(3分)下列计算正确的是( )
A. B.
C.x÷y D.
5.(3分)已知am=2,an=3,则a4m﹣3n的值是( )
A.﹣ B. C.﹣ D.
6.(3分)若△ABC≌△DEF,且△ABC的周长为20,AB=5,BC=8,则DF长为( )
A.5 B.8 C.7 D.5或8
7.(3分)A,B两地相距48千米,一艘轮船从A地顺流航行至B地,又立即从B地逆流返回A地,共用去9小时,已知水流速度为4千米/时,若设该轮船在静水中的速度为x千米/时,则可列方程( )
A. B.
C.+4=9 D.
8.(3分)已知等腰三角形的两边长分别为5和6,则这个等腰三角形的周长为( )
A.11 B.16 C.17 D.16或17
9.(3分)有下列命题:①两点之间,线段最短;②相等的角是对顶角;③内错角互补,两直线平行.其中真命题的有( )
A.1个 B.2个 C.3个 D.0个
二、填空题(共8小题,每小题3分,满分24分)
10.(3分)计算:(a﹣2)3= .
11.(3分)计算:+= .
12.(3分)用科学记数法表示:﹣0.00002016= .
13.(3分)如图,△ABC中,EF是AB的垂直平分线,与AB交于点D,BF=12,CF=3,则AC= .
14.(3分)将命题“互为相反数的两个数之和等于零”写成:如果 那么 .
15.(3分)化简:= .
16.(3分)已知﹣=3,则分式的值为 .
17.(3分)如图,AE∥BD,C是BD上的点,且AB=BC,∠ACD=110°,则∠EAB= 度.
三、解答题(满分66分)
18.(8分)计算:
(1)
(2).
19.(8分)解下列分式方程:
(1)
(2)
20.(8分)如图,△ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB于E,D为垂足,连接EC.
(1)求∠ECD的度数;
(2)若CE=5,求BC长.
21.(8分)先化简,再求值:选一个你所喜欢的数代入求值.
22.(10分)观察下面的变形规律:
=1﹣;=﹣;=﹣;…解答下面的问题:
(1)若n为正整数,请你猜想= ;
(2)求和:++.(注:只能用上述结论做才能给分);
(3)用上述相似的方法求和:+++…+.
23.(10分)去年入秋以来,某省发生了百年一遇的旱灾,连续8个多月无有效降水,为抗旱救灾,某部队计划为驻地村民新修水渠3600米,为了水渠能尽快投入使用,实际工作效率是原计划工作效率的1.8倍,结果提前20天完成修水渠任务.问原计划每天修水渠多少米?
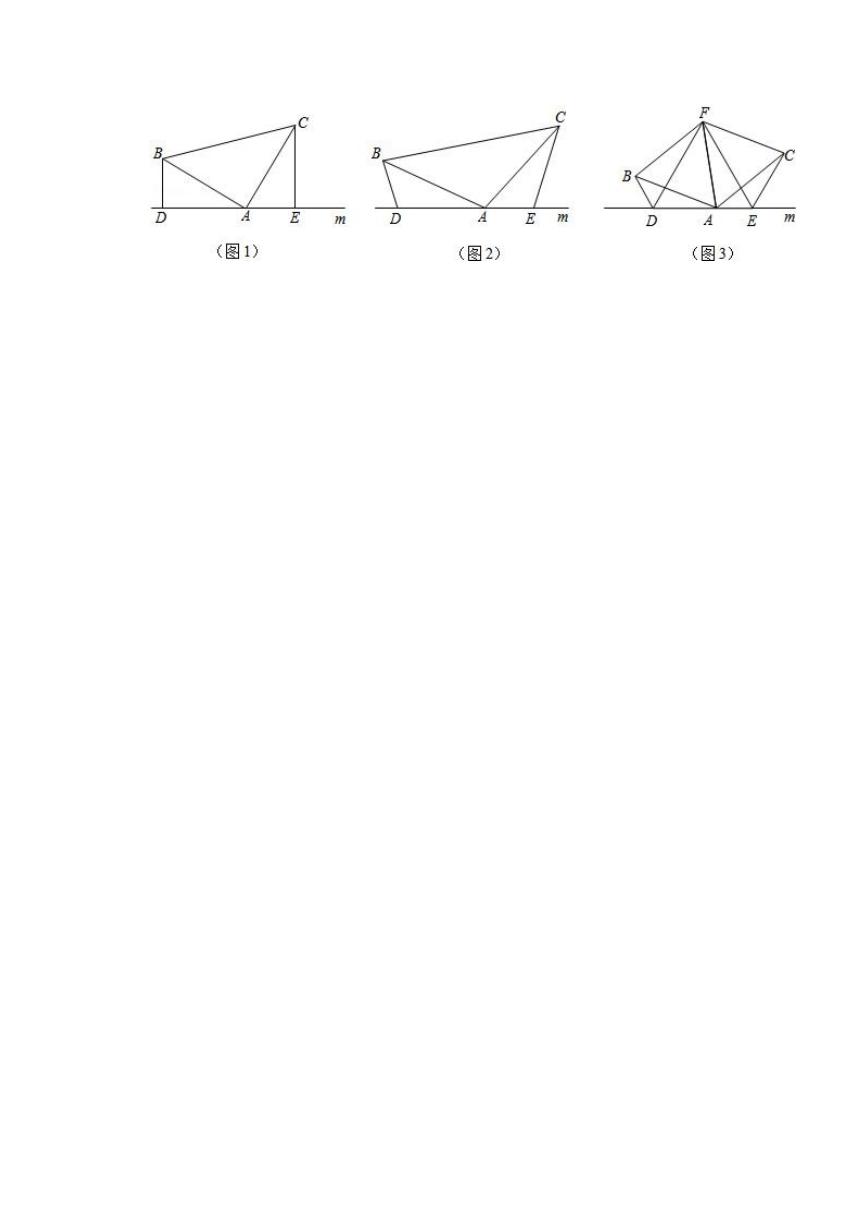
24.(14分)(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
(2)如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
(3)拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状.
2018-2019学年湖南省郴州市安仁县八年级(上)期中数学试卷
参考答案与试题解析
一、选择题(共9小题,每小题3分,满分27分)
1.(3分)下列各式:,,,,(x﹣y)中,是分式的共有( )
A.1个 B.2个 C.3个 D.4个
【分析】判断分式的依据是看分母中是否含有字母,如果含有字母则是分式,如果不含有字母则不是分式.
【解答】解:,,(x﹣y)是分式,
故选:C.
2.(3分)已知三角形的三边长分别为4,5,x,则x不可能是( )
A.3 B.5 C.7 D.9
【分析】已知两边时,第三边的范围是大于两边的差,小于两边的和.这样就可以确定x的范围,也就可以求出x的不可能取得的值.
【解答】解:5﹣4<x<5+4,即1<x<9,则x的不可能的值是9,
故选:D.
3.(3分)若分式的值为零,则x等于( )
A.0 B.2 C.±2 D.﹣2
【分析】根据分式值为零的条件可得x2﹣4=0,2x﹣4≠0,再解即可.
【解答】解:由题意得:x2﹣4=0,2x﹣4≠0,
解得:x=﹣2,
故选:D.
4.(3分)下列计算正确的是( )
A. B.
C.x÷y D.
【分析】原式各项计算得到结果,即可做出判断.
【解答】解:A、原式= =,错误;
B、原式=,正确;
C、原式=,错误;
D、原式==,错误,
故选:B.
5.(3分)已知am=2,an=3,则a4m﹣3n的值是( )
A.﹣ B. C.﹣ D.
【分析】根据同底数幂的除法法则和积的乘方和幂的乘方的运算法则求解.
【解答】解:∵am=2,an=3
∴a4m﹣3n=a4m÷a3n=(am)4÷(an)3=16÷27=.
故选:B.
6.(3分)若△ABC≌△DEF,且△ABC的周长为20,AB=5,BC=8,则DF长为( )
A.5 B.8 C.7 D.5或8
【分析】根据三角形的周长可得AC长,然后再利用全等三角形的性质可得DF长.
【解答】解:∵△ABC的周长为20,AB=5,BC=8,
∴AC=20﹣5﹣8=7,
∵△ABC≌△DEF,
∴DF=AC=7,
故选:C.
7.(3分)A,B两地相距48千米,一艘轮船从A地顺流航行至B地,又立即从B地逆流返回A地,共用去9小时,已知水流速度为4千米/时,若设该轮船在静水中的速度为x千米/时,则可列方程( )
A. B.
C.+4=9 D.
【分析】本题的等量关系为:顺流时间+逆流时间=9小时.
【解答】解:顺流时间为:;逆流时间为:.
所列方程为:+=9.
故选:A.
8.(3分)已知等腰三角形的两边长分别为5和6,则这个等腰三角形的周长为( )
A.11 B.16 C.17 D.16或17
【分析】分6是腰长和底边两种情况,利用三角形的三边关系判断,然后根据三角形的周长的定义列式计算即可得解.
【解答】解:①6是腰长时,三角形的三边分别为6、6、5,
能组成三角形,
周长=6+6+5=17;
②6是底边时,三角形的三边分别为6、5、5,
能组成三角形,
周长=6+5+5=16.
综上所述,三角形的周长为16或17.
故选:D.
9.(3分)有下列命题:①两点之间,线段最短;②相等的角是对顶角;③内错角互补,两直线平行.其中真命题的有( )
A.1个 B.2个 C.3个 D.0个
【分析】利用线段公理对①进行判断;根据对顶角的定义对②进行判断;根据平行线的判定方法对③进行判断.
【解答】解:两点之间,线段最短,所以①为真命题;
相等的角不一定是对顶角,所以②为假命题;
内错角相等,两直线平行.所以③为假命题.
故选:A.
二、填空题(共8小题,每小题3分,满分24分)
10.(3分)计算:(a﹣2)3= a﹣6 .
【分析】根据负整数指数幂的运算法则进行计算即可.
【解答】解:(a﹣2)3=a﹣6.
故答案为:a﹣6.
11.(3分)计算:+= 0 .
【分析】原式变形后,利用同分母分式的减法法则计算即可得到结果.
【解答】解:原式=﹣=0,
故答案为:0
12.(3分)用科学记数法表示:﹣0.00002016= ﹣2.016×10﹣5 .
【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.
【解答】解:﹣0.00002016=﹣2.016×10﹣5,
故答案为:﹣2.016×10﹣5.
13.(3分)如图,△ABC中,EF是AB的垂直平分线,与AB交于点D,BF=12,CF=3,则AC= 15 .
【分析】根据线段的垂直平分线的性质得到FA=BF,代入计算即可得到答案.
【解答】解:∵EF是AB的垂直平分线,
∴FA=BF=12,
∴AC=AF+FC=15.
故答案为:15.
14.(3分)将命题“互为相反数的两个数之和等于零”写成:如果 两个数互为相反数 那么 这两个数之和等于0 .
【分析】分清题设和结论即可写成如果…,那么…的形式.
【解答】解:互为相反数的两个数之和等于0”的题设是两个数互为相反数,结论是这两个数的和为0,
改写成如果…,那么…的形式为:如果两个数互为相反数,那么这两个数之和等于0,
故答案为:两个数互为相反数,这两个数之和等于0.
15.(3分)化简:= .
【分析】先利用完全平方公式进行因式分解,再约分求解即可.
【解答】解:==.
故答案为:.
16.(3分)已知﹣=3,则分式的值为 .
【分析】由已知条件可知xy≠0,根据分式的基本性质,先将分式的分子、分母同时除以xy,再把﹣=3代入即可.
【解答】解:∵﹣=3,
∴x≠0,y≠0,
∴xy≠0.
∴=====.
故答案为:.
17.(3分)如图,AE∥BD,C是BD上的点,且AB=BC,∠ACD=110°,则∠EAB= 40 度.
【分析】首先利用∠ACD=110°求得∠ACB与∠BAC的度数,然后利用三角形内角和定理求得∠B的度数,然后利用平行线的性质求得结论即可.
【解答】解:∵AB=BC,
∴∠ACB=∠BAC
∵∠ACD=110°
∴∠ACB=∠BAC=70°
∴∠B=∠40°,
∵AE∥BD,
∴∠EAB=40°,
故答案为40.
三、解答题(满分66分)
18.(8分)计算:
(1)
(2).
【分析】(1)原式利用零指数幂、负整数指数幂法则计算即可求出值;
(2)原式利用除法法则变形,约分即可得到结果.
【解答】解:(1)原式=﹣2﹣2+1=﹣3;
(2)原式= =.
19.(8分)解下列分式方程:
(1)
(2)
【分析】根据①去分母;②求出整式方程的解;③检验;④得出结论.
【解答】解:(1)
两边乘x(x﹣1)得到:3x﹣3=2x
解得x=3,
经检验:x=3是分式方程的解.
(2)
两边乘(x+1)(x﹣1)得到,3x﹣3+x+1=6,
解得x=2,
经检验:x=2是分式方程的解.
20.(8分)如图,△ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB于E,D为垂足,连接EC.
(1)求∠ECD的度数;
(2)若CE=5,求BC长.
【分析】(1)ED是AC的垂直平分线,可得AE=EC;∠A=∠C;已知∠A=36,即可求得;
(2)△ABC中,AB=AC,∠A=36°,可得∠B=72°又∠BEC=∠A+∠ECA=72°,所以,得BC=EC=5;
【解答】解:(1)∵DE垂直平分AC,
∴CE=AE,∴∠ECD=∠A=36°;
(2)∵AB=AC,∠A=36°,
∴∠B=∠ACB=72°,
∴∠BEC=∠A+∠ECD=72°,
∴∠BEC=∠B,
∴BC=EC=5.
答:(1)∠ECD的度数是36°;
(2)BC长是5.
21.(8分)先化简,再求值:选一个你所喜欢的数代入求值.
【分析】先根据分式混合运算的法则把原式进行化简,再选取合适的a的值代入进行计算即可.
【解答】解:
原式=×﹣,
=﹣,
=﹣,
当a=0时,原式=﹣.
22.(10分)观察下面的变形规律:
=1﹣;=﹣;=﹣;…解答下面的问题:
(1)若n为正整数,请你猜想= ﹣ ;
(2)求和:++.(注:只能用上述结论做才能给分);
(3)用上述相似的方法求和:+++…+.
【分析】(1)观察题目所给等式可直接写出.
(2)利用=﹣把++转换成1﹣+﹣+﹣后直接计算即可.
(3)仿照(2)将:+++…+转换成×(1﹣+﹣+﹣+…+﹣)就可轻易算出结果.
【解答】解:(1)答案为:﹣;
(2)++
=1﹣+﹣+﹣
=1﹣
=
(3)+++…+
=×(1﹣+﹣+﹣+…+﹣)
=×(1﹣)
=×
=
23.(10分)去年入秋以来,某省发生了百年一遇的旱灾,连续8个多月无有效降水,为抗旱救灾,某部队计划为驻地村民新修水渠3600米,为了水渠能尽快投入使用,实际工作效率是原计划工作效率的1.8倍,结果提前20天完成修水渠任务.问原计划每天修水渠多少米?
【分析】设原计划每天修水渠x米.根据原计划工作用的时间﹣实际工作用的时间=20等量关系列出方程.
【解答】解:设原计划每天修水渠x米.
根据题意得:﹣=20,
解得:x=80.
经检验:x=80是原分式方程的解.
答:原计划每天修水渠80米.
24.(14分)(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
(2)如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
(3)拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状.
【分析】(1)根据BD⊥直线m,CE⊥直线m得∠BDA=∠CEA=90°,而∠BAC=90°,根据等角的余角相等得∠CAE=∠ABD,然后根据“AAS”可判断△ADB≌△CEA,
则AE=BD,AD=CE,于是DE=AE+AD=BD+CE;
(2)与(1)的证明方法一样;
(3)由前面的结论得到△ADB≌△CEA,则BD=AE,∠DBA=∠CAE,根据等边三角形的性质得∠ABF=∠CAF=60°,则∠DBA+∠ABF=∠CAE+∠CAF,则∠DBF=∠FAE,
利用“SAS”可判断△DBF≌△EAF,所以DF=EF,∠BFD=∠AFE,于是∠DFE=∠DFA+∠AFE=∠DFA+∠BFD=60°,根据等边三角形的判定方法可得到△DEF为等边三角形.
【解答】证明:(1)∵BD⊥直线m,CE⊥直线m,
∴∠BDA=∠CEA=90°,
∵∠BAC=90°,
∴∠BAD+∠CAE=90°,
∵∠BAD+∠ABD=90°,
∴∠CAE=∠ABD,
∵在△ADB和△CEA中
,
∴△ADB≌△CEA(AAS),
∴AE=BD,AD=CE,
∴DE=AE+AD=BD+CE;
(2)成立.
∵∠BDA=∠BAC=α,
∴∠DBA+∠BAD=∠BAD+∠CAE=180°﹣α,
∴∠CAE=∠ABD,
∵在△ADB和△CEA中
,
∴△ADB≌△CEA(AAS),
∴AE=BD,AD=CE,
∴DE=AE+AD=BD+CE;
(3)△DEF是等边三角形.
由(2)知,△ADB≌△CEA,
BD=AE,∠DBA=∠CAE,
∵△ABF和△ACF均为等边三角形,
∴∠ABF=∠CAF=60°,
∴∠DBA+∠ABF=∠CAE+∠CAF,
∴∠DBF=∠FAE,
∵BF=AF
在△DBF和△EAF中
,
∴△DBF≌△EAF(SAS),
∴DF=EF,∠BFD=∠AFE,
∴∠DFE=∠DFA+∠AFE=∠DFA+∠BFD=60°,
∴△DEF为等边三角形.
一、选择题(共9小题,每小题3分,满分27分)
1.(3分)下列各式:,,,,(x﹣y)中,是分式的共有( )
A.1个 B.2个 C.3个 D.4个
2.(3分)已知三角形的三边长分别为4,5,x,则x不可能是( )
A.3 B.5 C.7 D.9
3.(3分)若分式的值为零,则x等于( )
A.0 B.2 C.±2 D.﹣2
4.(3分)下列计算正确的是( )
A. B.
C.x÷y D.
5.(3分)已知am=2,an=3,则a4m﹣3n的值是( )
A.﹣ B. C.﹣ D.
6.(3分)若△ABC≌△DEF,且△ABC的周长为20,AB=5,BC=8,则DF长为( )
A.5 B.8 C.7 D.5或8
7.(3分)A,B两地相距48千米,一艘轮船从A地顺流航行至B地,又立即从B地逆流返回A地,共用去9小时,已知水流速度为4千米/时,若设该轮船在静水中的速度为x千米/时,则可列方程( )
A. B.
C.+4=9 D.
8.(3分)已知等腰三角形的两边长分别为5和6,则这个等腰三角形的周长为( )
A.11 B.16 C.17 D.16或17
9.(3分)有下列命题:①两点之间,线段最短;②相等的角是对顶角;③内错角互补,两直线平行.其中真命题的有( )
A.1个 B.2个 C.3个 D.0个
二、填空题(共8小题,每小题3分,满分24分)
10.(3分)计算:(a﹣2)3= .
11.(3分)计算:+= .
12.(3分)用科学记数法表示:﹣0.00002016= .
13.(3分)如图,△ABC中,EF是AB的垂直平分线,与AB交于点D,BF=12,CF=3,则AC= .
14.(3分)将命题“互为相反数的两个数之和等于零”写成:如果 那么 .
15.(3分)化简:= .
16.(3分)已知﹣=3,则分式的值为 .
17.(3分)如图,AE∥BD,C是BD上的点,且AB=BC,∠ACD=110°,则∠EAB= 度.
三、解答题(满分66分)
18.(8分)计算:
(1)
(2).
19.(8分)解下列分式方程:
(1)
(2)
20.(8分)如图,△ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB于E,D为垂足,连接EC.
(1)求∠ECD的度数;
(2)若CE=5,求BC长.
21.(8分)先化简,再求值:选一个你所喜欢的数代入求值.
22.(10分)观察下面的变形规律:
=1﹣;=﹣;=﹣;…解答下面的问题:
(1)若n为正整数,请你猜想= ;
(2)求和:++.(注:只能用上述结论做才能给分);
(3)用上述相似的方法求和:+++…+.
23.(10分)去年入秋以来,某省发生了百年一遇的旱灾,连续8个多月无有效降水,为抗旱救灾,某部队计划为驻地村民新修水渠3600米,为了水渠能尽快投入使用,实际工作效率是原计划工作效率的1.8倍,结果提前20天完成修水渠任务.问原计划每天修水渠多少米?
24.(14分)(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
(2)如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
(3)拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状.
2018-2019学年湖南省郴州市安仁县八年级(上)期中数学试卷
参考答案与试题解析
一、选择题(共9小题,每小题3分,满分27分)
1.(3分)下列各式:,,,,(x﹣y)中,是分式的共有( )
A.1个 B.2个 C.3个 D.4个
【分析】判断分式的依据是看分母中是否含有字母,如果含有字母则是分式,如果不含有字母则不是分式.
【解答】解:,,(x﹣y)是分式,
故选:C.
2.(3分)已知三角形的三边长分别为4,5,x,则x不可能是( )
A.3 B.5 C.7 D.9
【分析】已知两边时,第三边的范围是大于两边的差,小于两边的和.这样就可以确定x的范围,也就可以求出x的不可能取得的值.
【解答】解:5﹣4<x<5+4,即1<x<9,则x的不可能的值是9,
故选:D.
3.(3分)若分式的值为零,则x等于( )
A.0 B.2 C.±2 D.﹣2
【分析】根据分式值为零的条件可得x2﹣4=0,2x﹣4≠0,再解即可.
【解答】解:由题意得:x2﹣4=0,2x﹣4≠0,
解得:x=﹣2,
故选:D.
4.(3分)下列计算正确的是( )
A. B.
C.x÷y D.
【分析】原式各项计算得到结果,即可做出判断.
【解答】解:A、原式= =,错误;
B、原式=,正确;
C、原式=,错误;
D、原式==,错误,
故选:B.
5.(3分)已知am=2,an=3,则a4m﹣3n的值是( )
A.﹣ B. C.﹣ D.
【分析】根据同底数幂的除法法则和积的乘方和幂的乘方的运算法则求解.
【解答】解:∵am=2,an=3
∴a4m﹣3n=a4m÷a3n=(am)4÷(an)3=16÷27=.
故选:B.
6.(3分)若△ABC≌△DEF,且△ABC的周长为20,AB=5,BC=8,则DF长为( )
A.5 B.8 C.7 D.5或8
【分析】根据三角形的周长可得AC长,然后再利用全等三角形的性质可得DF长.
【解答】解:∵△ABC的周长为20,AB=5,BC=8,
∴AC=20﹣5﹣8=7,
∵△ABC≌△DEF,
∴DF=AC=7,
故选:C.
7.(3分)A,B两地相距48千米,一艘轮船从A地顺流航行至B地,又立即从B地逆流返回A地,共用去9小时,已知水流速度为4千米/时,若设该轮船在静水中的速度为x千米/时,则可列方程( )
A. B.
C.+4=9 D.
【分析】本题的等量关系为:顺流时间+逆流时间=9小时.
【解答】解:顺流时间为:;逆流时间为:.
所列方程为:+=9.
故选:A.
8.(3分)已知等腰三角形的两边长分别为5和6,则这个等腰三角形的周长为( )
A.11 B.16 C.17 D.16或17
【分析】分6是腰长和底边两种情况,利用三角形的三边关系判断,然后根据三角形的周长的定义列式计算即可得解.
【解答】解:①6是腰长时,三角形的三边分别为6、6、5,
能组成三角形,
周长=6+6+5=17;
②6是底边时,三角形的三边分别为6、5、5,
能组成三角形,
周长=6+5+5=16.
综上所述,三角形的周长为16或17.
故选:D.
9.(3分)有下列命题:①两点之间,线段最短;②相等的角是对顶角;③内错角互补,两直线平行.其中真命题的有( )
A.1个 B.2个 C.3个 D.0个
【分析】利用线段公理对①进行判断;根据对顶角的定义对②进行判断;根据平行线的判定方法对③进行判断.
【解答】解:两点之间,线段最短,所以①为真命题;
相等的角不一定是对顶角,所以②为假命题;
内错角相等,两直线平行.所以③为假命题.
故选:A.
二、填空题(共8小题,每小题3分,满分24分)
10.(3分)计算:(a﹣2)3= a﹣6 .
【分析】根据负整数指数幂的运算法则进行计算即可.
【解答】解:(a﹣2)3=a﹣6.
故答案为:a﹣6.
11.(3分)计算:+= 0 .
【分析】原式变形后,利用同分母分式的减法法则计算即可得到结果.
【解答】解:原式=﹣=0,
故答案为:0
12.(3分)用科学记数法表示:﹣0.00002016= ﹣2.016×10﹣5 .
【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.
【解答】解:﹣0.00002016=﹣2.016×10﹣5,
故答案为:﹣2.016×10﹣5.
13.(3分)如图,△ABC中,EF是AB的垂直平分线,与AB交于点D,BF=12,CF=3,则AC= 15 .
【分析】根据线段的垂直平分线的性质得到FA=BF,代入计算即可得到答案.
【解答】解:∵EF是AB的垂直平分线,
∴FA=BF=12,
∴AC=AF+FC=15.
故答案为:15.
14.(3分)将命题“互为相反数的两个数之和等于零”写成:如果 两个数互为相反数 那么 这两个数之和等于0 .
【分析】分清题设和结论即可写成如果…,那么…的形式.
【解答】解:互为相反数的两个数之和等于0”的题设是两个数互为相反数,结论是这两个数的和为0,
改写成如果…,那么…的形式为:如果两个数互为相反数,那么这两个数之和等于0,
故答案为:两个数互为相反数,这两个数之和等于0.
15.(3分)化简:= .
【分析】先利用完全平方公式进行因式分解,再约分求解即可.
【解答】解:==.
故答案为:.
16.(3分)已知﹣=3,则分式的值为 .
【分析】由已知条件可知xy≠0,根据分式的基本性质,先将分式的分子、分母同时除以xy,再把﹣=3代入即可.
【解答】解:∵﹣=3,
∴x≠0,y≠0,
∴xy≠0.
∴=====.
故答案为:.
17.(3分)如图,AE∥BD,C是BD上的点,且AB=BC,∠ACD=110°,则∠EAB= 40 度.
【分析】首先利用∠ACD=110°求得∠ACB与∠BAC的度数,然后利用三角形内角和定理求得∠B的度数,然后利用平行线的性质求得结论即可.
【解答】解:∵AB=BC,
∴∠ACB=∠BAC
∵∠ACD=110°
∴∠ACB=∠BAC=70°
∴∠B=∠40°,
∵AE∥BD,
∴∠EAB=40°,
故答案为40.
三、解答题(满分66分)
18.(8分)计算:
(1)
(2).
【分析】(1)原式利用零指数幂、负整数指数幂法则计算即可求出值;
(2)原式利用除法法则变形,约分即可得到结果.
【解答】解:(1)原式=﹣2﹣2+1=﹣3;
(2)原式= =.
19.(8分)解下列分式方程:
(1)
(2)
【分析】根据①去分母;②求出整式方程的解;③检验;④得出结论.
【解答】解:(1)
两边乘x(x﹣1)得到:3x﹣3=2x
解得x=3,
经检验:x=3是分式方程的解.
(2)
两边乘(x+1)(x﹣1)得到,3x﹣3+x+1=6,
解得x=2,
经检验:x=2是分式方程的解.
20.(8分)如图,△ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB于E,D为垂足,连接EC.
(1)求∠ECD的度数;
(2)若CE=5,求BC长.
【分析】(1)ED是AC的垂直平分线,可得AE=EC;∠A=∠C;已知∠A=36,即可求得;
(2)△ABC中,AB=AC,∠A=36°,可得∠B=72°又∠BEC=∠A+∠ECA=72°,所以,得BC=EC=5;
【解答】解:(1)∵DE垂直平分AC,
∴CE=AE,∴∠ECD=∠A=36°;
(2)∵AB=AC,∠A=36°,
∴∠B=∠ACB=72°,
∴∠BEC=∠A+∠ECD=72°,
∴∠BEC=∠B,
∴BC=EC=5.
答:(1)∠ECD的度数是36°;
(2)BC长是5.
21.(8分)先化简,再求值:选一个你所喜欢的数代入求值.
【分析】先根据分式混合运算的法则把原式进行化简,再选取合适的a的值代入进行计算即可.
【解答】解:
原式=×﹣,
=﹣,
=﹣,
当a=0时,原式=﹣.
22.(10分)观察下面的变形规律:
=1﹣;=﹣;=﹣;…解答下面的问题:
(1)若n为正整数,请你猜想= ﹣ ;
(2)求和:++.(注:只能用上述结论做才能给分);
(3)用上述相似的方法求和:+++…+.
【分析】(1)观察题目所给等式可直接写出.
(2)利用=﹣把++转换成1﹣+﹣+﹣后直接计算即可.
(3)仿照(2)将:+++…+转换成×(1﹣+﹣+﹣+…+﹣)就可轻易算出结果.
【解答】解:(1)答案为:﹣;
(2)++
=1﹣+﹣+﹣
=1﹣
=
(3)+++…+
=×(1﹣+﹣+﹣+…+﹣)
=×(1﹣)
=×
=
23.(10分)去年入秋以来,某省发生了百年一遇的旱灾,连续8个多月无有效降水,为抗旱救灾,某部队计划为驻地村民新修水渠3600米,为了水渠能尽快投入使用,实际工作效率是原计划工作效率的1.8倍,结果提前20天完成修水渠任务.问原计划每天修水渠多少米?
【分析】设原计划每天修水渠x米.根据原计划工作用的时间﹣实际工作用的时间=20等量关系列出方程.
【解答】解:设原计划每天修水渠x米.
根据题意得:﹣=20,
解得:x=80.
经检验:x=80是原分式方程的解.
答:原计划每天修水渠80米.
24.(14分)(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
(2)如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
(3)拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状.
【分析】(1)根据BD⊥直线m,CE⊥直线m得∠BDA=∠CEA=90°,而∠BAC=90°,根据等角的余角相等得∠CAE=∠ABD,然后根据“AAS”可判断△ADB≌△CEA,
则AE=BD,AD=CE,于是DE=AE+AD=BD+CE;
(2)与(1)的证明方法一样;
(3)由前面的结论得到△ADB≌△CEA,则BD=AE,∠DBA=∠CAE,根据等边三角形的性质得∠ABF=∠CAF=60°,则∠DBA+∠ABF=∠CAE+∠CAF,则∠DBF=∠FAE,
利用“SAS”可判断△DBF≌△EAF,所以DF=EF,∠BFD=∠AFE,于是∠DFE=∠DFA+∠AFE=∠DFA+∠BFD=60°,根据等边三角形的判定方法可得到△DEF为等边三角形.
【解答】证明:(1)∵BD⊥直线m,CE⊥直线m,
∴∠BDA=∠CEA=90°,
∵∠BAC=90°,
∴∠BAD+∠CAE=90°,
∵∠BAD+∠ABD=90°,
∴∠CAE=∠ABD,
∵在△ADB和△CEA中
,
∴△ADB≌△CEA(AAS),
∴AE=BD,AD=CE,
∴DE=AE+AD=BD+CE;
(2)成立.
∵∠BDA=∠BAC=α,
∴∠DBA+∠BAD=∠BAD+∠CAE=180°﹣α,
∴∠CAE=∠ABD,
∵在△ADB和△CEA中
,
∴△ADB≌△CEA(AAS),
∴AE=BD,AD=CE,
∴DE=AE+AD=BD+CE;
(3)△DEF是等边三角形.
由(2)知,△ADB≌△CEA,
BD=AE,∠DBA=∠CAE,
∵△ABF和△ACF均为等边三角形,
∴∠ABF=∠CAF=60°,
∴∠DBA+∠ABF=∠CAE+∠CAF,
∴∠DBF=∠FAE,
∵BF=AF
在△DBF和△EAF中
,
∴△DBF≌△EAF(SAS),
∴DF=EF,∠BFD=∠AFE,
∴∠DFE=∠DFA+∠AFE=∠DFA+∠BFD=60°,
∴△DEF为等边三角形.
同课章节目录
