全等三角形的判定(SSS)
图片预览




文档简介
(共27张PPT)
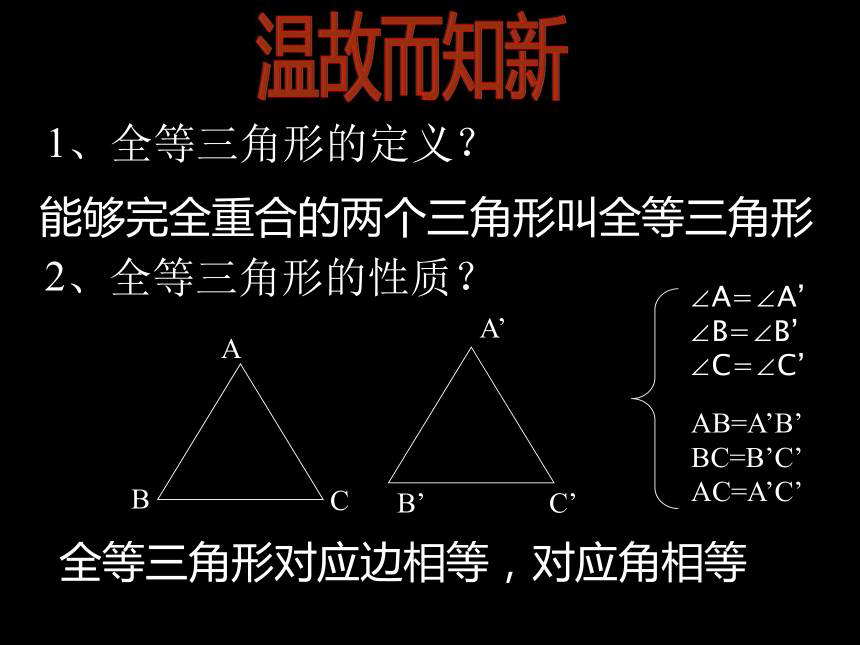
1、全等三角形的定义?
能够完全重合的两个三角形叫全等三角形
2、全等三角形的性质?
A
B
C
A’
B’
C’
∠A=∠A’
∠B=∠B’
∠C=∠C’
AB=A’B’
BC=B’C’
AC=A’C’
全等三角形对应边相等,对应角相等
金昌市第三中学 王鹏程
学习目标
1、掌握“边边边”条件的内容;
2、能初步应用“边边边”条件判定两个三角形全等.
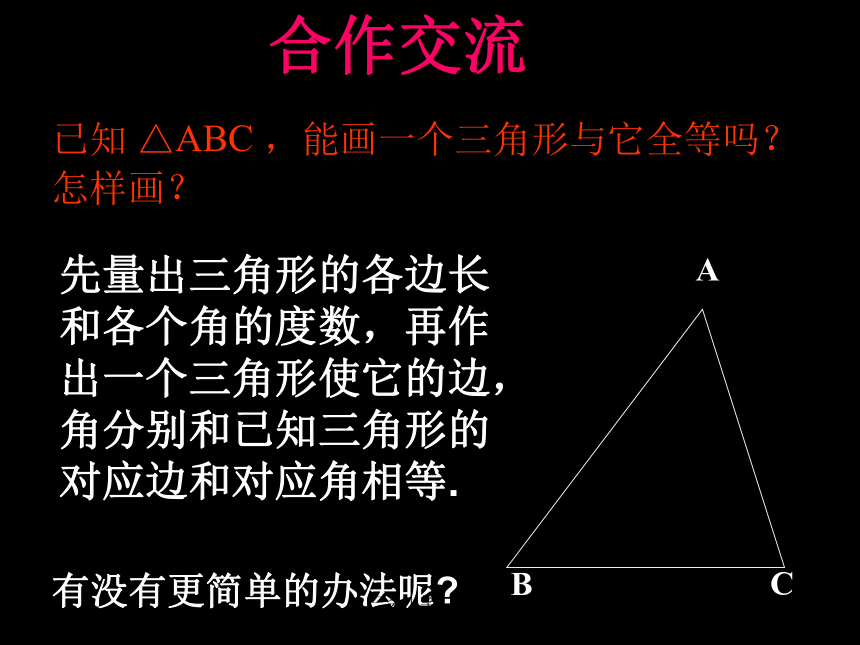
已知 △ABC ,能画一个三角形与它全等吗?
怎样画?
先量出三角形的各边长和各个角的度数,再作出一个三角形使它的边,角分别和已知三角形的对应边和对应角相等.
有没有更简单的办法呢
A
B
C
合作交流
导学
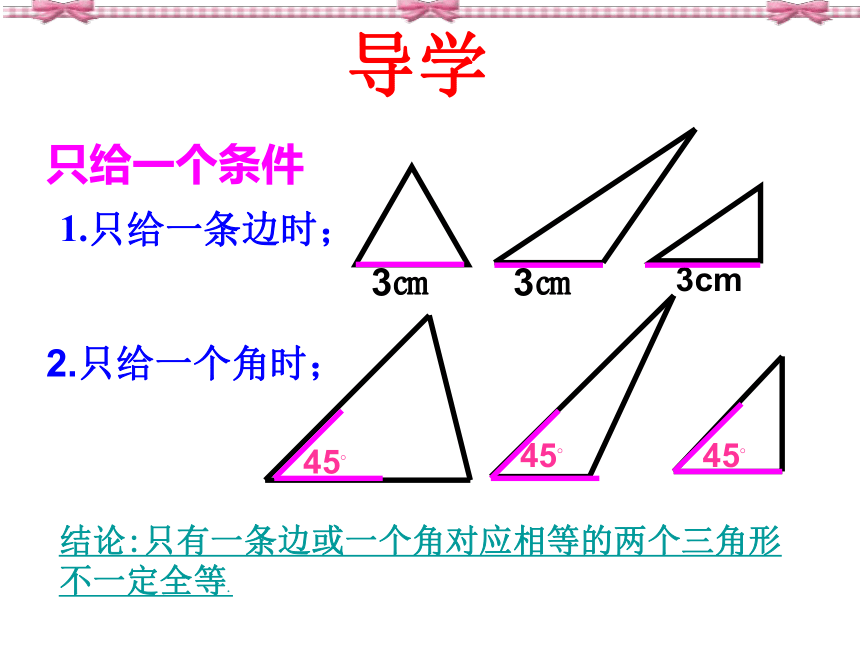
1.只给一条边时;
3㎝
3㎝
只给一个条件
45
45
2.只给一个角时;
3cm
45
结论:只有一条边或一个角对应相等的两个三角形 不一定全等.
如果给出两个条件画三角形,
你能说出有哪几种可能的情况?
①两边;
③两角。
②一边一角;
①如果三角形的两边分别为4cm,6cm 时
6cm
6cm
4cm
4cm
结论:两条边对应相等的两个三角形不一定全等.
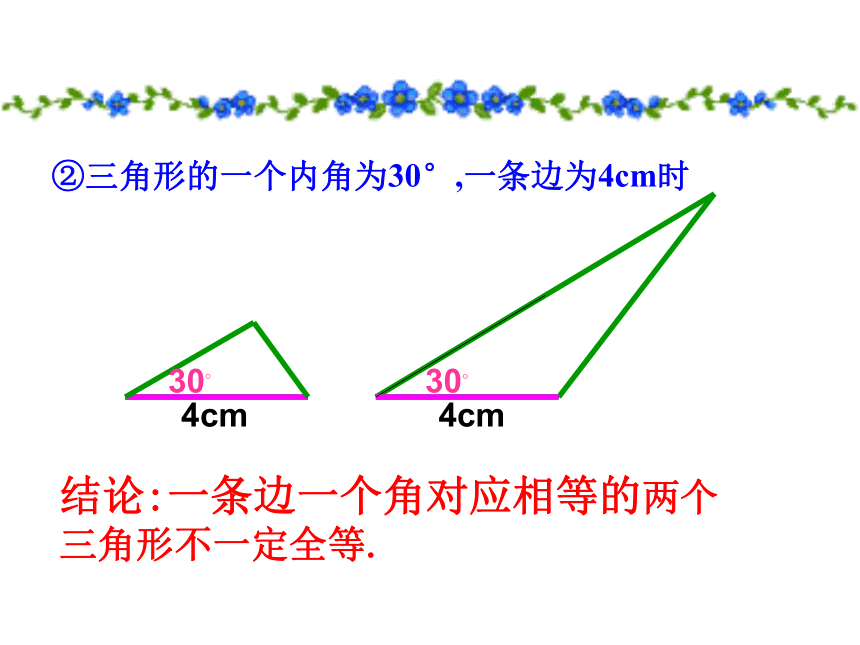
②三角形的一个内角为30°,一条边为4cm时
4cm
4cm
30
30
结论:一条边一个角对应相等的两个三角形不一定全等.
45
30
45
30
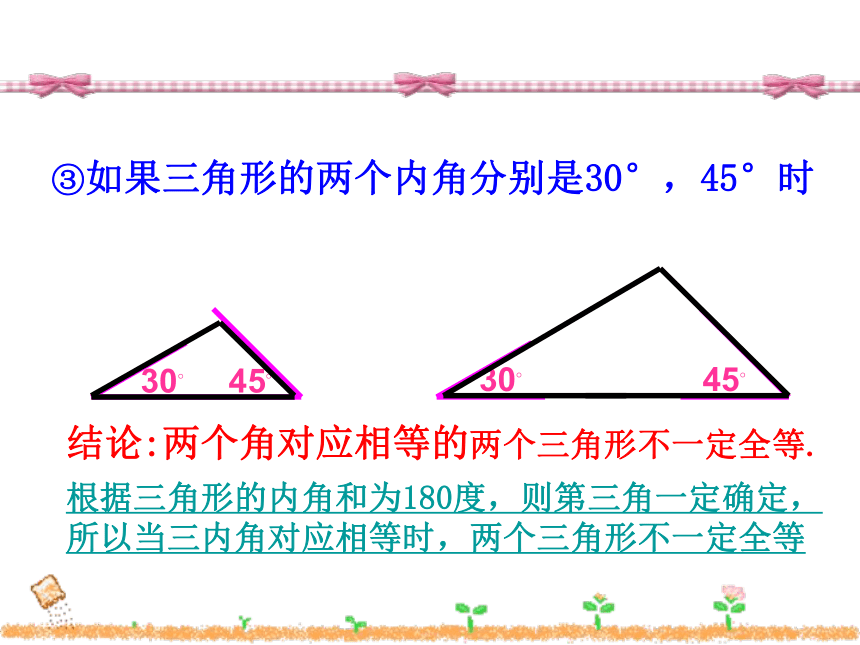
③如果三角形的两个内角分别是30°,45°时
结论:两个角对应相等的两个三角形不一定全等.
根据三角形的内角和为180度,则第三角一定确定,所以当三内角对应相等时,两个三角形不一定全等
两个条件
①两角;
②两边;
③一边一角。
结论:只给出一个或两个条件时,都不能保证所画的三角形一定全等。
一个条件
①一角;
②一边;
如果给出三个条件画三角形,
你能说出有哪几种可能的情况?
①三边;
②三角;
③两边一角;
④两角一边。
自学
自学课本第6页“探究2”至第7页“例1”的内容,然后完成下列问题:
1.如何任意画一个△ABC,再画一个△A′B′C′,
使AB=A′B′,BC=B′C′,CA=C′A′,请你给出一种画法.
2.由“探究2”你能得到什么结论?
展示提升
自学课本第6页“探究2”至第7页“例1”的内容,然后完成下列问题:
1.如何任意画一个△ABC,再画一个△A′B′C′,
使AB=A′B′,BC=B′C′,CA=C′A′,请你给出一种画法.
2.由“探究2”你能得到什么结论?
例1:如图,△ABC是一个钢架,AB=AC,AD是连接点A与BC中点D的支架.求证:△ABD △ACD
A
B
C
D
分析:要证△ABD △ACD,可看这两个三角形的三条边是否对应相等
证明:∵ D是BC的中点
∴ BD=CD
在△ABC和△ACD中,
AB=AC (已知)
BD=CD (已证)
AD=AD (公共边)
∴ △ABD △ACD (SSS)
巩固生成
本课你有什么收获
本节课我们讨论了判定三角形全等的
一个方法,根据课前的探究你能不能
试着找出其他的判定方法?
作业:
习题11.2第2、9题写作业本上.
2、画出一个三角形,使它的三边长分别为3cm、 4cm、6cm ,把你画的三角形与小组内画的进行比较,它们一定全等吗?
画法: 1.画线段AB=3㎝;
2.分别以A、B为圆心,4㎝和6㎝长为半径画弧,两弧交于点C;
3. 连接线段AC、BC.
结论:三边对应相等的两个三角形全等.
可简写为边边边或SSS
思考:你能用三角形的稳定性来说明SSS公理吗
探究一:
任意画△ABC,再画△A′B′C′,使AB=A′B′,BC=B′C′,我们观察这样画的两个三角形是否一定全等
A
B
C
A′
B′
C′
AB=A′B′ BC=B′C′
思考:满足这样一些条件是否能成立?
三角形的两个角分别是30°、50°
三角形两条边分别是4cm,6cm
三角形的一个角为30°,一条边为3cm
探究二:
任意画一个△ABC,再画一个△A′B′C′,使AB=A′B′,BC=B′C′,CA=C′A′,判断两个三角形是否全等
作法:1、画线段B′C=BC;
2、分别以B′、C′为圆心,线段AB、BC为半径作弧,两弧交于点A′;
3、连接线段A′B′,A′C′。
结论:三边对应相等的两个三角形全等 简写为:
SSS
由上面的结论我们可以看出三边对应相等的两个三角形全等。我们可以用这个结论来判断两个三角形是否全等,我们把判断两个三角形全等的推理过程,叫做证明三角形的全等。
三角形全等判定一:
边对应相等的两个三角形全等
简写:SSS
小结
例1:如图,△ABC是一个钢架,AB=AC,AD是连接点A与BC中点D的支架。求证∴
A
B
C
D
分析:要证△ABD △ACD,可看这两个三角形的三条边是否对应相等
证明:∵ D是BC的中点
∴ BD=CD
在△ABC和△ACD中,
AB=AC (已知)
BD=CD (已证)
AD=AD (公共边)
∴ △ABD △ACD (SSS)
我们利用前面的结论,还可以得到作一个角等于已知角的方法。
例2:已知∠AOB
求作:∠A′O′B′=∠AOB
O
A
B
C
D
O′
A′
B′
C′
D′
作法:1、以点O为圆心,任意长为半径画弧,分别交OA,OB于点C、D;
2、画一条射线O′A′,以点O′为圆心,OC长为半径画弧,交O′A′于点C′;
3、以点C′为圆心,CD长为半径画弧,与第2步中所画的弧交于点D′;
4、过点D′画射线O′B′,则∠A′O′B′=∠AOB
教材第15页习题11.2中的第1、2题。
本课你有什么收获
1、判断两个三角形是否全等至少要三对对应相等的条件(除特殊直角三角形外)
2、全等三角形的判定(一)
三边对应相等的两个三角形全等
简写:SSS
作业:
习题11.2第9题
1、全等三角形的定义?
能够完全重合的两个三角形叫全等三角形
2、全等三角形的性质?
A
B
C
A’
B’
C’
∠A=∠A’
∠B=∠B’
∠C=∠C’
AB=A’B’
BC=B’C’
AC=A’C’
全等三角形对应边相等,对应角相等
金昌市第三中学 王鹏程
学习目标
1、掌握“边边边”条件的内容;
2、能初步应用“边边边”条件判定两个三角形全等.
已知 △ABC ,能画一个三角形与它全等吗?
怎样画?
先量出三角形的各边长和各个角的度数,再作出一个三角形使它的边,角分别和已知三角形的对应边和对应角相等.
有没有更简单的办法呢
A
B
C
合作交流
导学
1.只给一条边时;
3㎝
3㎝
只给一个条件
45
45
2.只给一个角时;
3cm
45
结论:只有一条边或一个角对应相等的两个三角形 不一定全等.
如果给出两个条件画三角形,
你能说出有哪几种可能的情况?
①两边;
③两角。
②一边一角;
①如果三角形的两边分别为4cm,6cm 时
6cm
6cm
4cm
4cm
结论:两条边对应相等的两个三角形不一定全等.
②三角形的一个内角为30°,一条边为4cm时
4cm
4cm
30
30
结论:一条边一个角对应相等的两个三角形不一定全等.
45
30
45
30
③如果三角形的两个内角分别是30°,45°时
结论:两个角对应相等的两个三角形不一定全等.
根据三角形的内角和为180度,则第三角一定确定,所以当三内角对应相等时,两个三角形不一定全等
两个条件
①两角;
②两边;
③一边一角。
结论:只给出一个或两个条件时,都不能保证所画的三角形一定全等。
一个条件
①一角;
②一边;
如果给出三个条件画三角形,
你能说出有哪几种可能的情况?
①三边;
②三角;
③两边一角;
④两角一边。
自学
自学课本第6页“探究2”至第7页“例1”的内容,然后完成下列问题:
1.如何任意画一个△ABC,再画一个△A′B′C′,
使AB=A′B′,BC=B′C′,CA=C′A′,请你给出一种画法.
2.由“探究2”你能得到什么结论?
展示提升
自学课本第6页“探究2”至第7页“例1”的内容,然后完成下列问题:
1.如何任意画一个△ABC,再画一个△A′B′C′,
使AB=A′B′,BC=B′C′,CA=C′A′,请你给出一种画法.
2.由“探究2”你能得到什么结论?
例1:如图,△ABC是一个钢架,AB=AC,AD是连接点A与BC中点D的支架.求证:△ABD △ACD
A
B
C
D
分析:要证△ABD △ACD,可看这两个三角形的三条边是否对应相等
证明:∵ D是BC的中点
∴ BD=CD
在△ABC和△ACD中,
AB=AC (已知)
BD=CD (已证)
AD=AD (公共边)
∴ △ABD △ACD (SSS)
巩固生成
本课你有什么收获
本节课我们讨论了判定三角形全等的
一个方法,根据课前的探究你能不能
试着找出其他的判定方法?
作业:
习题11.2第2、9题写作业本上.
2、画出一个三角形,使它的三边长分别为3cm、 4cm、6cm ,把你画的三角形与小组内画的进行比较,它们一定全等吗?
画法: 1.画线段AB=3㎝;
2.分别以A、B为圆心,4㎝和6㎝长为半径画弧,两弧交于点C;
3. 连接线段AC、BC.
结论:三边对应相等的两个三角形全等.
可简写为边边边或SSS
思考:你能用三角形的稳定性来说明SSS公理吗
探究一:
任意画△ABC,再画△A′B′C′,使AB=A′B′,BC=B′C′,我们观察这样画的两个三角形是否一定全等
A
B
C
A′
B′
C′
AB=A′B′ BC=B′C′
思考:满足这样一些条件是否能成立?
三角形的两个角分别是30°、50°
三角形两条边分别是4cm,6cm
三角形的一个角为30°,一条边为3cm
探究二:
任意画一个△ABC,再画一个△A′B′C′,使AB=A′B′,BC=B′C′,CA=C′A′,判断两个三角形是否全等
作法:1、画线段B′C=BC;
2、分别以B′、C′为圆心,线段AB、BC为半径作弧,两弧交于点A′;
3、连接线段A′B′,A′C′。
结论:三边对应相等的两个三角形全等 简写为:
SSS
由上面的结论我们可以看出三边对应相等的两个三角形全等。我们可以用这个结论来判断两个三角形是否全等,我们把判断两个三角形全等的推理过程,叫做证明三角形的全等。
三角形全等判定一:
边对应相等的两个三角形全等
简写:SSS
小结
例1:如图,△ABC是一个钢架,AB=AC,AD是连接点A与BC中点D的支架。求证∴
A
B
C
D
分析:要证△ABD △ACD,可看这两个三角形的三条边是否对应相等
证明:∵ D是BC的中点
∴ BD=CD
在△ABC和△ACD中,
AB=AC (已知)
BD=CD (已证)
AD=AD (公共边)
∴ △ABD △ACD (SSS)
我们利用前面的结论,还可以得到作一个角等于已知角的方法。
例2:已知∠AOB
求作:∠A′O′B′=∠AOB
O
A
B
C
D
O′
A′
B′
C′
D′
作法:1、以点O为圆心,任意长为半径画弧,分别交OA,OB于点C、D;
2、画一条射线O′A′,以点O′为圆心,OC长为半径画弧,交O′A′于点C′;
3、以点C′为圆心,CD长为半径画弧,与第2步中所画的弧交于点D′;
4、过点D′画射线O′B′,则∠A′O′B′=∠AOB
教材第15页习题11.2中的第1、2题。
本课你有什么收获
1、判断两个三角形是否全等至少要三对对应相等的条件(除特殊直角三角形外)
2、全等三角形的判定(一)
三边对应相等的两个三角形全等
简写:SSS
作业:
习题11.2第9题
