正多边形和圆及一些圆的综合知识点概括
图片预览




文档简介
(共30张PPT)
正多边形与圆
林佳俊
今天学习的任务
1,圆的周长,面积,弧长,圆心角,弦心距
2,圆与圆的位置关系,线与圆的位置关系
3,扇形面积,弓形面积
4,正多边形的定义,对称性,中心,半径,边长,边心距, 内角和,内角,外角,中心角
5,正多边形与圆的计算题
6,正多边形与圆的证明题
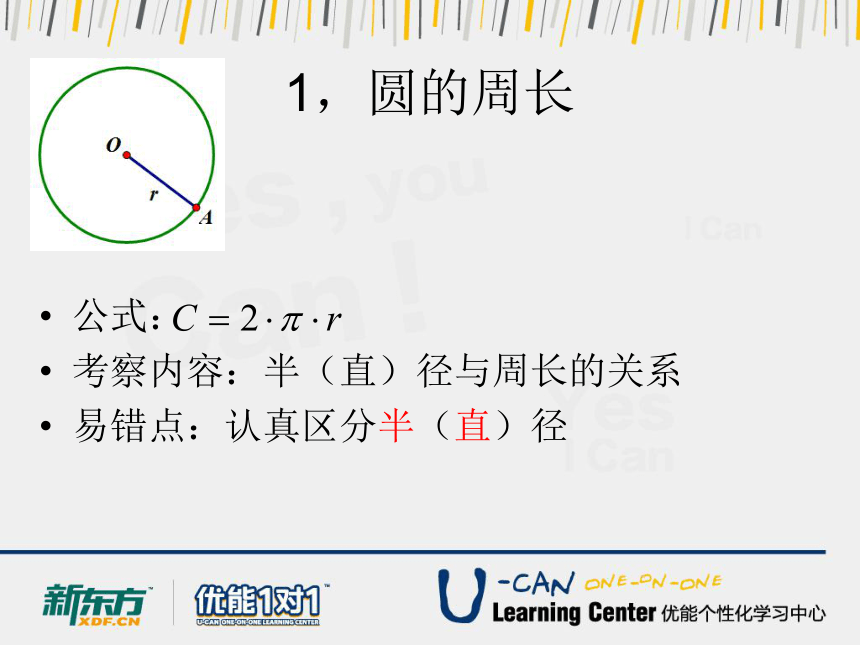
1,圆的周长
公式:
考察内容:半(直)径与周长的关系
易错点:认真区分半(直)径
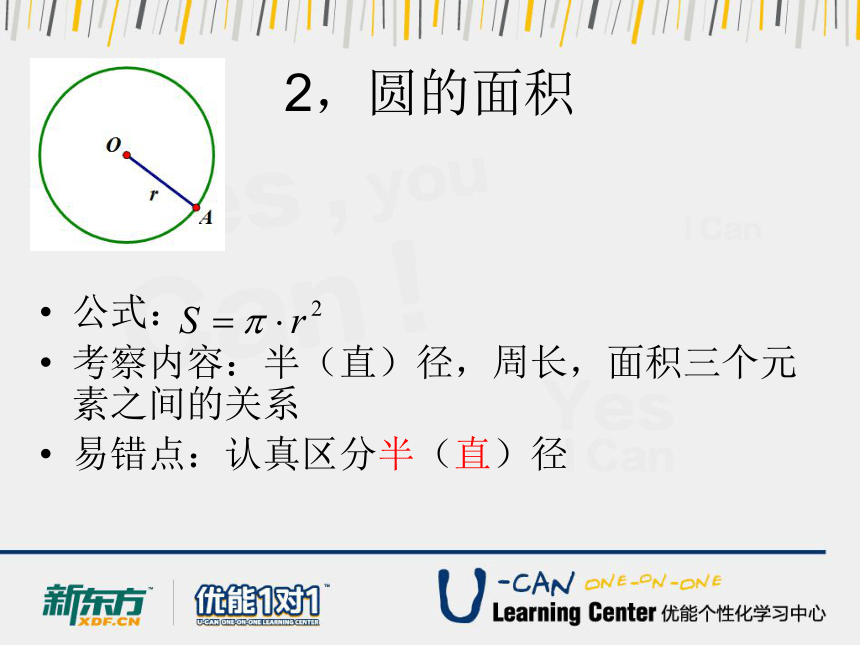
2,圆的面积
公式:
考察内容:半(直)径,周长,面积三个元素之间的关系
易错点:认真区分半(直)径
3,圆的弧长和圆心角
公式:
考察内容:半(直)径,弧长,圆周角三个元素之间的转换,区分优弧和劣弧
易错点:公式后半部分是圆的周长公式不是面积公式,区分半(直)径
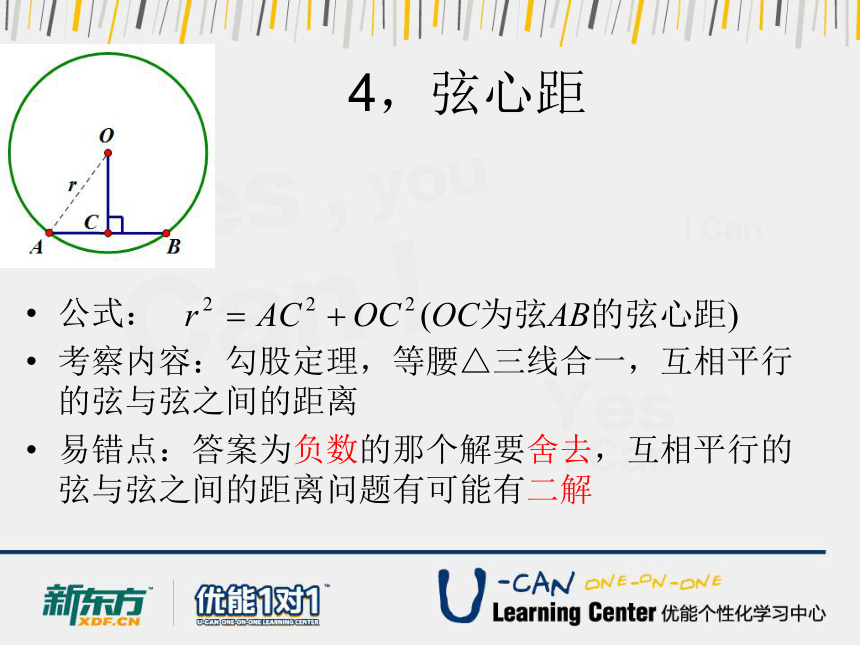
4,弦心距
公式:
考察内容:勾股定理,等腰△三线合一,互相平行的弦与弦之间的距离
易错点:答案为负数的那个解要舍去,互相平行的弦与弦之间的距离问题有可能有二解
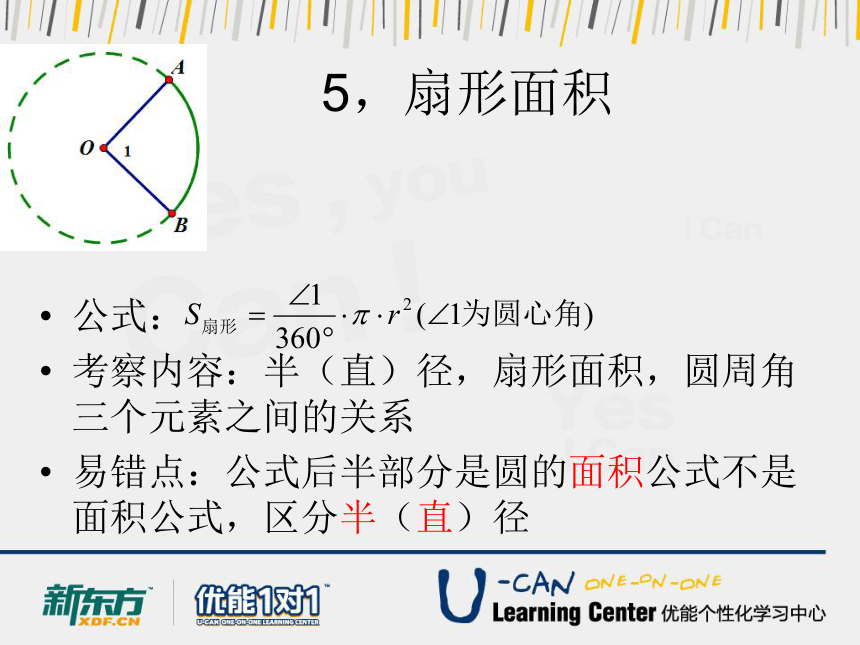
5,扇形面积
公式:
考察内容:半(直)径,扇形面积,圆周角三个元素之间的关系
易错点:公式后半部分是圆的面积公式不是面积公式,区分半(直)径
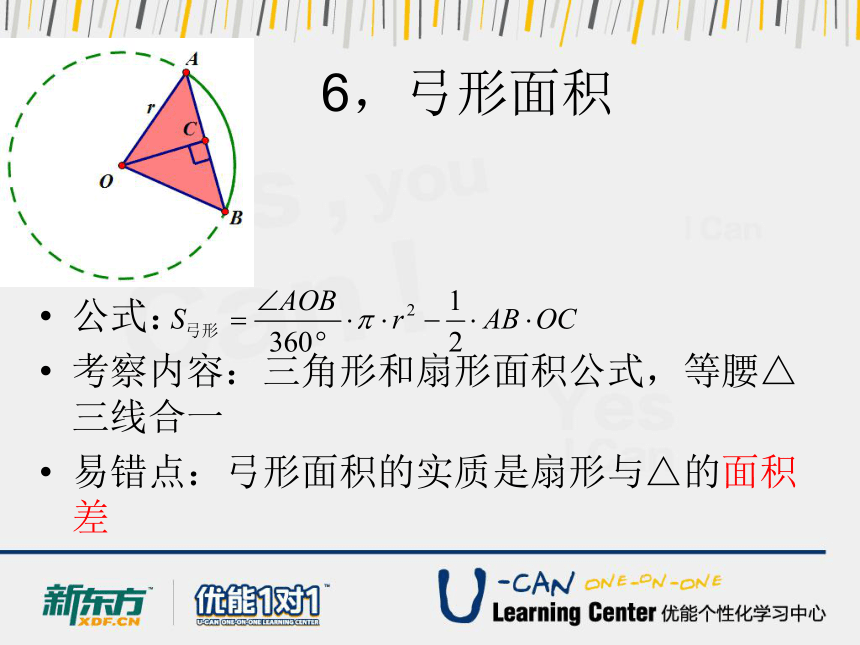
6,弓形面积
公式:
考察内容:三角形和扇形面积公式,等腰△三线合一
易错点:弓形面积的实质是扇形与△的面积差
7,圆与圆相离
条件:
考察内容:圆与圆相离的条件
易错点:区别外切,相离时的圆心距是绝对不能取到等号的
8,圆与圆外切
条件:
考察内容:圆与圆相切的条件
易错点:当题目条件给出相切时,要注意有可能有内切和外切两解
9,圆与圆相交
条件:
考察内容:圆与圆相交的条件
易错点:相交是介于内切与外切之间
10,圆与圆内切
条件:
考察内容:圆与圆相交的条件
易错点:当题目条件给出相切时,要注意有可能有内切和外切两解
11,圆与圆内含
条件:
考察内容:圆与圆内含的条件
易错点:同心是内含的特殊情况,所以等号一定要取
12,圆与圆同心
条件:
考察内容:圆与圆同心的条件
易错点:同心是内含的特殊情况,同心一定内含,但内含不一定同心
13,直线与圆相离
条件:直线AB与圆O没有交点
考察内容:直线与圆相离的判断条件
易错点:在直角坐标系的题目中,通常利用圆心到直线的距离来判断,若距离>r则为相离
14,直线与圆相切
条件:直线AB与圆O只有1个交点或AB⊥OC(r)
考察内容:直线与圆相切的判断条件
易错点:在直角坐标系的题目中,通常利用圆心到直线的距离来判断,若距离=r则为相离,有时也能通过二元一次方程△=0来做
15,直线与圆相交
条件:直线AB与圆O有2个交点
考察内容:直线与圆相交的判断条件
易错点:在直角坐标系的题目中,通常利用圆心到直线的距离来判断,若0≤距离16,正多边形的定义
定义:各边相等,各角也相等的多边形叫做正多边形(多边形:边数大于等于3)。
考察内容:根据条件判断是否为正多边形
易错点:边和角要同时满足相等才是正多边形,每个边数相等的正多边形都是相似的
17,正n边形的对称性(奇数)
定义:对称轴的条数为n,且为轴对称图形
考察内容:正确判断对称性,以及对称轴的数量
易错点:边为奇偶数所导致的对称性不同
18,正n边形的对称性(偶数)
定义:对称轴的条数为n,且即为轴对称图形,又为中心对称图形
考察内容:正确判断对称性,以及对称轴的数量
易错点:边为奇偶数所导致的对称性不同
19,正多边形的中心,半径和边长
定义:O为中心,r为半径,AB为边长
考察内容:半径平分正多边形的内角,区分中心,半径,边长,
易错点:任何正多边形的边长可以和两条半径构成等腰△,正六边形可以构成等边△
20,正多边形的边心距
公式:内切圆半径r为边心距
考察内容:边长⊥于边心距,等腰△三线合一
易错点:等腰△三线合一,内切圆和外切圆是同心关系
21,正多边形内角和
公式:
考察内容:熟练掌握公式,内角和与边的关系
小技巧:任何正n边形都能切割成(n-2)个△,所以内角和为
22,正多边形的内角
公式:
考察内容:熟练掌握公式,内角与边的关系
小技巧:任何正n边形都能切割成(n-2)个
△,所以内角为
23,正多边形的外角
公式:
考察内容:熟练掌握公式,外角与边的关系
易错点:区分所求条件是外角还是内角
24,正多边形的中心角
公式:
考察内容:熟练掌握公式,中心角与边的关系
小技巧:中心角=外角
正多边形与圆
林佳俊
今天学习的任务
1,圆的周长,面积,弧长,圆心角,弦心距
2,圆与圆的位置关系,线与圆的位置关系
3,扇形面积,弓形面积
4,正多边形的定义,对称性,中心,半径,边长,边心距, 内角和,内角,外角,中心角
5,正多边形与圆的计算题
6,正多边形与圆的证明题
1,圆的周长
公式:
考察内容:半(直)径与周长的关系
易错点:认真区分半(直)径
2,圆的面积
公式:
考察内容:半(直)径,周长,面积三个元素之间的关系
易错点:认真区分半(直)径
3,圆的弧长和圆心角
公式:
考察内容:半(直)径,弧长,圆周角三个元素之间的转换,区分优弧和劣弧
易错点:公式后半部分是圆的周长公式不是面积公式,区分半(直)径
4,弦心距
公式:
考察内容:勾股定理,等腰△三线合一,互相平行的弦与弦之间的距离
易错点:答案为负数的那个解要舍去,互相平行的弦与弦之间的距离问题有可能有二解
5,扇形面积
公式:
考察内容:半(直)径,扇形面积,圆周角三个元素之间的关系
易错点:公式后半部分是圆的面积公式不是面积公式,区分半(直)径
6,弓形面积
公式:
考察内容:三角形和扇形面积公式,等腰△三线合一
易错点:弓形面积的实质是扇形与△的面积差
7,圆与圆相离
条件:
考察内容:圆与圆相离的条件
易错点:区别外切,相离时的圆心距是绝对不能取到等号的
8,圆与圆外切
条件:
考察内容:圆与圆相切的条件
易错点:当题目条件给出相切时,要注意有可能有内切和外切两解
9,圆与圆相交
条件:
考察内容:圆与圆相交的条件
易错点:相交是介于内切与外切之间
10,圆与圆内切
条件:
考察内容:圆与圆相交的条件
易错点:当题目条件给出相切时,要注意有可能有内切和外切两解
11,圆与圆内含
条件:
考察内容:圆与圆内含的条件
易错点:同心是内含的特殊情况,所以等号一定要取
12,圆与圆同心
条件:
考察内容:圆与圆同心的条件
易错点:同心是内含的特殊情况,同心一定内含,但内含不一定同心
13,直线与圆相离
条件:直线AB与圆O没有交点
考察内容:直线与圆相离的判断条件
易错点:在直角坐标系的题目中,通常利用圆心到直线的距离来判断,若距离>r则为相离
14,直线与圆相切
条件:直线AB与圆O只有1个交点或AB⊥OC(r)
考察内容:直线与圆相切的判断条件
易错点:在直角坐标系的题目中,通常利用圆心到直线的距离来判断,若距离=r则为相离,有时也能通过二元一次方程△=0来做
15,直线与圆相交
条件:直线AB与圆O有2个交点
考察内容:直线与圆相交的判断条件
易错点:在直角坐标系的题目中,通常利用圆心到直线的距离来判断,若0≤距离
定义:各边相等,各角也相等的多边形叫做正多边形(多边形:边数大于等于3)。
考察内容:根据条件判断是否为正多边形
易错点:边和角要同时满足相等才是正多边形,每个边数相等的正多边形都是相似的
17,正n边形的对称性(奇数)
定义:对称轴的条数为n,且为轴对称图形
考察内容:正确判断对称性,以及对称轴的数量
易错点:边为奇偶数所导致的对称性不同
18,正n边形的对称性(偶数)
定义:对称轴的条数为n,且即为轴对称图形,又为中心对称图形
考察内容:正确判断对称性,以及对称轴的数量
易错点:边为奇偶数所导致的对称性不同
19,正多边形的中心,半径和边长
定义:O为中心,r为半径,AB为边长
考察内容:半径平分正多边形的内角,区分中心,半径,边长,
易错点:任何正多边形的边长可以和两条半径构成等腰△,正六边形可以构成等边△
20,正多边形的边心距
公式:内切圆半径r为边心距
考察内容:边长⊥于边心距,等腰△三线合一
易错点:等腰△三线合一,内切圆和外切圆是同心关系
21,正多边形内角和
公式:
考察内容:熟练掌握公式,内角和与边的关系
小技巧:任何正n边形都能切割成(n-2)个△,所以内角和为
22,正多边形的内角
公式:
考察内容:熟练掌握公式,内角与边的关系
小技巧:任何正n边形都能切割成(n-2)个
△,所以内角为
23,正多边形的外角
公式:
考察内容:熟练掌握公式,外角与边的关系
易错点:区分所求条件是外角还是内角
24,正多边形的中心角
公式:
考察内容:熟练掌握公式,中心角与边的关系
小技巧:中心角=外角
