正多边形和圆配套练习
图片预览







文档简介
(共20张PPT)
正多边形与圆精选练习
林佳俊
练习内容
1,圆的周长,面积,弧长,圆心角,弦心距
2,圆与圆的位置关系,线与圆的位置关系
3,扇形面积,弓形面积
4,正多边形的定义,对称性,中心,半径,边长,边心距, 内角和,内角,外角,中心角
1,圆的周长
1,圆的半径与周长成()
A,正比例 B,反比例 C不成比例关系
提示:辨识成正比例的量与反比例的量,尤其注意π是实数常量不是未知数。做完后还能尝试着求一下具体的比值为多少
2,如图,边长为8厘米的正方形周长比圆的周长长多少厘米?
提示:正多边形的边长于内切圆的半径的关系,尤其注意正四边形的
边长为2r,正六边形的边长为r
2,圆的面积
1,如图,阴影部分面积是大正方形的25%,是圆面积的 ,则圆面积是大正方形面积的多少倍?
提示:由于题中没有任何关于边长的已知量可以尝试着设正方形的边长为1,通
过已知条件以及面积公式便能得出圆的半径
2,一个圆的周长等于一个正方形的周长,那么
该圆的面积()该正方形
A,大于 B,小于 C,等于
提示:同上可以尝试着设正方形的边长为1从而表示出圆的半径,最后对面积进行比较
3,一个正方形的面积是40平方厘米,用该正方形剪出一个周长最大的圆,剪成的圆的面积是多少
提示:圆与圆是互相相似的,所以周长最大的圆也意味着面积也是最大的,所以该圆为正方形的内接圆,同学们该题做完后同时能考虑一下如果是矩形该怎么减
3,圆的弧长和圆心角
1,如图,半径都为1的三个圆两两相交,且弧AB=弧BC=弧AC,CD的弧长等于 ,则图中阴影部分的面积为多少
提示:此题难度较大,我们首先要看出阴影部分是由3个这样的图形拼成的
由此想到只需将圆减去左下图两倍的阴影部分即可得到,而那个
阴影部分的面积恰恰是一段弓形的面积,而角 可以利用弧长公
式得到
4,弦心距
1,圆O的半径为5,弦AB的弦心距为3,则AB为多少
提示:利用勾股定理求的是AC的长度,而题目要求的是弦AB的长度要看
清题目
2,圆O的半径为5,弦AB的长度为8,
弦CD∥于弦AB且到弦AB的距离为1,
求弦CD的弦心距?
提示:要画出图像,弦心距的题目极有可能会有2解,但有时也有可能1解或者不存在,具体要视题目而定
5,扇形面积
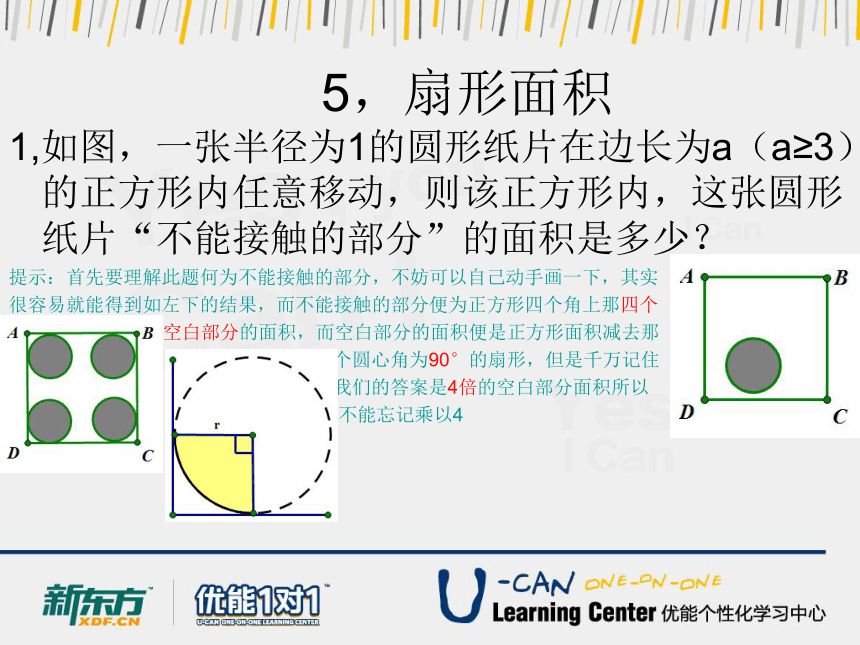
1,如图,一张半径为1的圆形纸片在边长为a(a≥3)的正方形内任意移动,则该正方形内,这张圆形纸片“不能接触的部分”的面积是多少?
提示:首先要理解此题何为不能接触的部分,不妨可以自己动手画一下,其实
很容易就能得到如左下的结果,而不能接触的部分便为正方形四个角上那四个
空白部分的面积,而空白部分的面积便是正方形面积减去那
个圆心角为90°的扇形,但是千万记住
我们的答案是4倍的空白部分面积所以
不能忘记乘以4
6,弓形面积
1,在圆中,弦长为2且半径为2围成的弓形面积为多少?
提示:由于根据弓形的面积=扇形面积-△面积,所以首先要得到扇形所对的
圆心角,再根据半径以及弦长所以很容易得到圆心角为60°,以及三角形的
面积
2,如图,点A,B,C在半径为2的圆O上,
四边形OABC是菱形,那么弧BC和弦BC所组成的弓形面积是?
提示:根据菱形的性质,可以容易得到△OCB为等
边△,由此圆心角以及三角形面积便容易得到
7,圆与圆的位置关系
1,已知圆A和圆B相切,圆心距为10cm,圆A的半径为3cm,则圆B的半径为?
提示:此题由于没有说明两圆是正切还是内切,故一定要两种情况都讨论
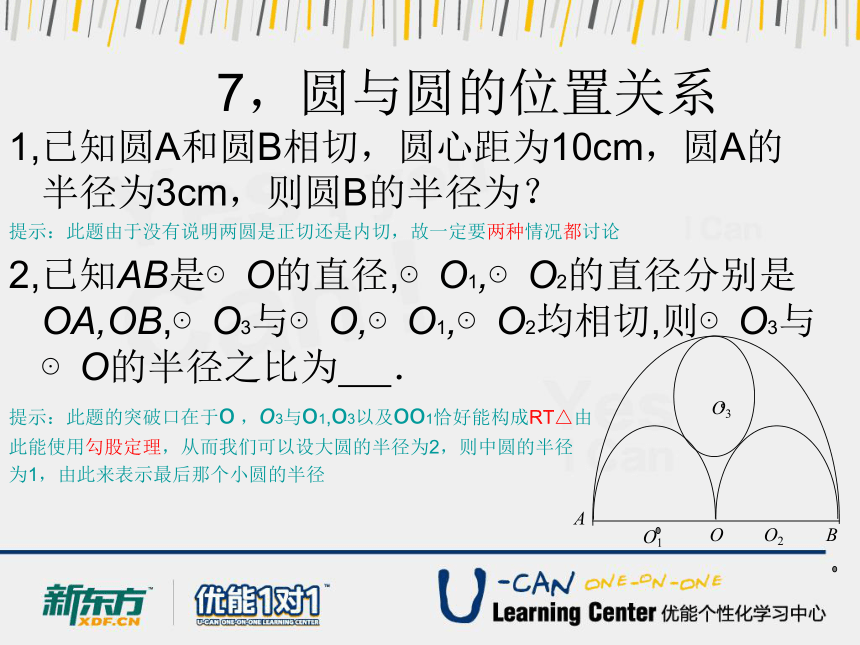
2,已知AB是⊙O的直径,⊙O1,⊙O2的直径分别是OA,OB,⊙O3与⊙O,⊙O1,⊙O2均相切,则⊙O3与⊙O的半径之比为 .
提示:此题的突破口在于o ,o3与o1,o3以及oo1恰好能构成RT△由
此能使用勾股定理,从而我们可以设大圆的半径为2,则中圆的半径
为1,由此来表示最后那个小圆的半径
A
B
O
O1
O2
O3
3,如图,点A,B在直线MN上,AB=11厘米,⊙A,⊙B的半径均为1厘米.⊙A以每秒2厘米的速度自左向右运动,与此同时,⊙B的径也不断增大,其半径r(厘米)与时间t(秒)之间的关系式为r=1+t(t≥0)
点A出发后多少秒后两圆相切?
提示:此题难度很大,因为讨论的情况很多,但是只要清楚的知道圆A运动情况以及圆B的变化状况那就解题轻而易举了,首先圆A从左边开始运动,先会与圆B左边外切,随后又会与圆B左边内切,接着会与圆B右边内切,最后与圆B右边外切,但是我们要注意了圆B的半径是变化的所以我们可以建立直角坐标系来处理就比较直观了
8,直线与圆的位置关系
1,已知⊙O的半径是5,圆心O到直线AB的距离为2,则⊙O上有且只有( )个点到直线AB的距离为3
提示:此题属于直线与圆一题多解的典型题目,通常我们要讨论在圆的
优弧和劣弧两边都要讨论因为此类题目极有可能4解或者3解,不要忘讨
论一边
9,正多边形的定义
1,各边相等的多边形一定是正多边形,是否正确?
提示:所有边和所有内角都相等多边形才是正多边形,反例如右图所示
2,所有内角相等的多边形一定是正多边
形,是否正确?
提示:所有边和所有内角都相等多边形才是正多边形,反例如下图所示
10,正n边形的对称性
1,一个正多边形绕它的中心旋转45°后,就与原正多边形第一次重合,那么这个正多边形( )
A.是轴对称图形,但不是中心对称图形
B.是中心对称图形,但不是轴对称图形
C.既是轴对称图形,又是中心对称图形
D.既不是轴对称图形,也不是中心对称图形
提示:根据题目可以得出该正多边形的中心角为45°,由此可以得出该多边形的
边数,由于正多边形的边数为奇数时,其仅为轴对称图形,若边数为偶数时,其
即为轴对称图形又为中心对称图形
11,正多边形的中心,半径和边长
1,已知正多边形的半径与边长相等,那么正多边形的边数是( )
A,4 B,5 C,6 D,8
提示:容易得到该正多边形的两条半径以及一条边长可以构成等边△,
所以可以得到该正多边形的中心角为60°,由此可以使用中心角公式
12,正多边形的边心距
1,已知正多边形的边心距与边长的比为 ,
则此正多边形的边数为( )
提示:由于两条半径与一条边长能构成一个等腰△,所以利用
等腰△三线合一的性质以及已知条件容易得到该等腰△为等腰RT△,
再利用中心角公式能得到边数
2.一正多边形的一个外角为90°,则它的边心距与半径之比为( )
A,1:2 B,1: C,1: D,1:3
提示:根据外角能得出内角的大小,所以容易确定该正多边形为正方形,画图后问题能引刃而解
13,正多边形内角
1,一个正多边形的内角和为2160°求它每个内角的度数
提示:根据多边形内角和的公式可以先得出边再把内角和除以边数即可得到最后的答案
2,只用一种正多边形可以铺满地板,这样的正多边形有( )
提示:此题需要理解题意,其实就是
内角为360°的因数,这样才能无缝
衔接
14,正多边形的内角和
1,一个正多边形的所有对角线都相等,则这个正多边形的内角和为()
提示:每个正多边形有(n-3)条对角线,由此可以想到满足条件的正多
边形可能为正方形或者正五边形,再利用内角和的公式进行计算
2,正多边形的内角和等于1440°
那么这个正多边形的边数为()
提示:根据内角和的公式可以逆运算得到边数,不过要看清题目是
内角还是内角和
15,正多边形的外角
1,外角大于内角的正多边形是( )
提示:随着正多边形的边数的增加,外角越来越小,但外角与内角的和始终是180°,而正方形是外角等于内角的,所以只有正三角形是外角大于内角的
2,内角比外角大60°的正多边形的边数是多少?
提示:可以结合正多边形内角和外角的公式,从而列出一个关于边数n的一元一次方程,从而问题便能迎刃而解
3,用两种正多边形镶嵌,不能与正三角形匹配的正多边形是()
A,正方形 B,正六边形 C,正十二边形 D,正十八边形
提示:可以设能匹配的正多边形的内角为x°,因为能与正三角形匹配所以ax+60b=360°,其中a,x,b必须取正整数,而我们可以利用内角公式把选项中的那些正多边形的内角算出来由此代入即可得到哪种情况下是去a,b无法都取到正整数的。
16,正多边形的中心角
1,正多边形的一边所对的中心角与该正多边形的一个内角的关系是( )
A,两角互余 B,两角互补 C,两角互余或互补 D,两角相等
提示:如图很容易得到结论 ,同时我们也要牢记结论正多边
形的中心角=外角
正多边形与圆精选练习
林佳俊
练习内容
1,圆的周长,面积,弧长,圆心角,弦心距
2,圆与圆的位置关系,线与圆的位置关系
3,扇形面积,弓形面积
4,正多边形的定义,对称性,中心,半径,边长,边心距, 内角和,内角,外角,中心角
1,圆的周长
1,圆的半径与周长成()
A,正比例 B,反比例 C不成比例关系
提示:辨识成正比例的量与反比例的量,尤其注意π是实数常量不是未知数。做完后还能尝试着求一下具体的比值为多少
2,如图,边长为8厘米的正方形周长比圆的周长长多少厘米?
提示:正多边形的边长于内切圆的半径的关系,尤其注意正四边形的
边长为2r,正六边形的边长为r
2,圆的面积
1,如图,阴影部分面积是大正方形的25%,是圆面积的 ,则圆面积是大正方形面积的多少倍?
提示:由于题中没有任何关于边长的已知量可以尝试着设正方形的边长为1,通
过已知条件以及面积公式便能得出圆的半径
2,一个圆的周长等于一个正方形的周长,那么
该圆的面积()该正方形
A,大于 B,小于 C,等于
提示:同上可以尝试着设正方形的边长为1从而表示出圆的半径,最后对面积进行比较
3,一个正方形的面积是40平方厘米,用该正方形剪出一个周长最大的圆,剪成的圆的面积是多少
提示:圆与圆是互相相似的,所以周长最大的圆也意味着面积也是最大的,所以该圆为正方形的内接圆,同学们该题做完后同时能考虑一下如果是矩形该怎么减
3,圆的弧长和圆心角
1,如图,半径都为1的三个圆两两相交,且弧AB=弧BC=弧AC,CD的弧长等于 ,则图中阴影部分的面积为多少
提示:此题难度较大,我们首先要看出阴影部分是由3个这样的图形拼成的
由此想到只需将圆减去左下图两倍的阴影部分即可得到,而那个
阴影部分的面积恰恰是一段弓形的面积,而角 可以利用弧长公
式得到
4,弦心距
1,圆O的半径为5,弦AB的弦心距为3,则AB为多少
提示:利用勾股定理求的是AC的长度,而题目要求的是弦AB的长度要看
清题目
2,圆O的半径为5,弦AB的长度为8,
弦CD∥于弦AB且到弦AB的距离为1,
求弦CD的弦心距?
提示:要画出图像,弦心距的题目极有可能会有2解,但有时也有可能1解或者不存在,具体要视题目而定
5,扇形面积
1,如图,一张半径为1的圆形纸片在边长为a(a≥3)的正方形内任意移动,则该正方形内,这张圆形纸片“不能接触的部分”的面积是多少?
提示:首先要理解此题何为不能接触的部分,不妨可以自己动手画一下,其实
很容易就能得到如左下的结果,而不能接触的部分便为正方形四个角上那四个
空白部分的面积,而空白部分的面积便是正方形面积减去那
个圆心角为90°的扇形,但是千万记住
我们的答案是4倍的空白部分面积所以
不能忘记乘以4
6,弓形面积
1,在圆中,弦长为2且半径为2围成的弓形面积为多少?
提示:由于根据弓形的面积=扇形面积-△面积,所以首先要得到扇形所对的
圆心角,再根据半径以及弦长所以很容易得到圆心角为60°,以及三角形的
面积
2,如图,点A,B,C在半径为2的圆O上,
四边形OABC是菱形,那么弧BC和弦BC所组成的弓形面积是?
提示:根据菱形的性质,可以容易得到△OCB为等
边△,由此圆心角以及三角形面积便容易得到
7,圆与圆的位置关系
1,已知圆A和圆B相切,圆心距为10cm,圆A的半径为3cm,则圆B的半径为?
提示:此题由于没有说明两圆是正切还是内切,故一定要两种情况都讨论
2,已知AB是⊙O的直径,⊙O1,⊙O2的直径分别是OA,OB,⊙O3与⊙O,⊙O1,⊙O2均相切,则⊙O3与⊙O的半径之比为 .
提示:此题的突破口在于o ,o3与o1,o3以及oo1恰好能构成RT△由
此能使用勾股定理,从而我们可以设大圆的半径为2,则中圆的半径
为1,由此来表示最后那个小圆的半径
A
B
O
O1
O2
O3
3,如图,点A,B在直线MN上,AB=11厘米,⊙A,⊙B的半径均为1厘米.⊙A以每秒2厘米的速度自左向右运动,与此同时,⊙B的径也不断增大,其半径r(厘米)与时间t(秒)之间的关系式为r=1+t(t≥0)
点A出发后多少秒后两圆相切?
提示:此题难度很大,因为讨论的情况很多,但是只要清楚的知道圆A运动情况以及圆B的变化状况那就解题轻而易举了,首先圆A从左边开始运动,先会与圆B左边外切,随后又会与圆B左边内切,接着会与圆B右边内切,最后与圆B右边外切,但是我们要注意了圆B的半径是变化的所以我们可以建立直角坐标系来处理就比较直观了
8,直线与圆的位置关系
1,已知⊙O的半径是5,圆心O到直线AB的距离为2,则⊙O上有且只有( )个点到直线AB的距离为3
提示:此题属于直线与圆一题多解的典型题目,通常我们要讨论在圆的
优弧和劣弧两边都要讨论因为此类题目极有可能4解或者3解,不要忘讨
论一边
9,正多边形的定义
1,各边相等的多边形一定是正多边形,是否正确?
提示:所有边和所有内角都相等多边形才是正多边形,反例如右图所示
2,所有内角相等的多边形一定是正多边
形,是否正确?
提示:所有边和所有内角都相等多边形才是正多边形,反例如下图所示
10,正n边形的对称性
1,一个正多边形绕它的中心旋转45°后,就与原正多边形第一次重合,那么这个正多边形( )
A.是轴对称图形,但不是中心对称图形
B.是中心对称图形,但不是轴对称图形
C.既是轴对称图形,又是中心对称图形
D.既不是轴对称图形,也不是中心对称图形
提示:根据题目可以得出该正多边形的中心角为45°,由此可以得出该多边形的
边数,由于正多边形的边数为奇数时,其仅为轴对称图形,若边数为偶数时,其
即为轴对称图形又为中心对称图形
11,正多边形的中心,半径和边长
1,已知正多边形的半径与边长相等,那么正多边形的边数是( )
A,4 B,5 C,6 D,8
提示:容易得到该正多边形的两条半径以及一条边长可以构成等边△,
所以可以得到该正多边形的中心角为60°,由此可以使用中心角公式
12,正多边形的边心距
1,已知正多边形的边心距与边长的比为 ,
则此正多边形的边数为( )
提示:由于两条半径与一条边长能构成一个等腰△,所以利用
等腰△三线合一的性质以及已知条件容易得到该等腰△为等腰RT△,
再利用中心角公式能得到边数
2.一正多边形的一个外角为90°,则它的边心距与半径之比为( )
A,1:2 B,1: C,1: D,1:3
提示:根据外角能得出内角的大小,所以容易确定该正多边形为正方形,画图后问题能引刃而解
13,正多边形内角
1,一个正多边形的内角和为2160°求它每个内角的度数
提示:根据多边形内角和的公式可以先得出边再把内角和除以边数即可得到最后的答案
2,只用一种正多边形可以铺满地板,这样的正多边形有( )
提示:此题需要理解题意,其实就是
内角为360°的因数,这样才能无缝
衔接
14,正多边形的内角和
1,一个正多边形的所有对角线都相等,则这个正多边形的内角和为()
提示:每个正多边形有(n-3)条对角线,由此可以想到满足条件的正多
边形可能为正方形或者正五边形,再利用内角和的公式进行计算
2,正多边形的内角和等于1440°
那么这个正多边形的边数为()
提示:根据内角和的公式可以逆运算得到边数,不过要看清题目是
内角还是内角和
15,正多边形的外角
1,外角大于内角的正多边形是( )
提示:随着正多边形的边数的增加,外角越来越小,但外角与内角的和始终是180°,而正方形是外角等于内角的,所以只有正三角形是外角大于内角的
2,内角比外角大60°的正多边形的边数是多少?
提示:可以结合正多边形内角和外角的公式,从而列出一个关于边数n的一元一次方程,从而问题便能迎刃而解
3,用两种正多边形镶嵌,不能与正三角形匹配的正多边形是()
A,正方形 B,正六边形 C,正十二边形 D,正十八边形
提示:可以设能匹配的正多边形的内角为x°,因为能与正三角形匹配所以ax+60b=360°,其中a,x,b必须取正整数,而我们可以利用内角公式把选项中的那些正多边形的内角算出来由此代入即可得到哪种情况下是去a,b无法都取到正整数的。
16,正多边形的中心角
1,正多边形的一边所对的中心角与该正多边形的一个内角的关系是( )
A,两角互余 B,两角互补 C,两角互余或互补 D,两角相等
提示:如图很容易得到结论 ,同时我们也要牢记结论正多边
形的中心角=外角
