正多边形和圆的证明题与计算题
图片预览




文档简介
(共22张PPT)
正多边形与圆 的证明以及计算
林佳俊
练习的内容
1,正多边形与圆的证明题
中考模拟题,难题,以及真题
2,正多边形与圆的计算题
中考模拟题,难题,以及真题
1,正多边形与圆的证明题
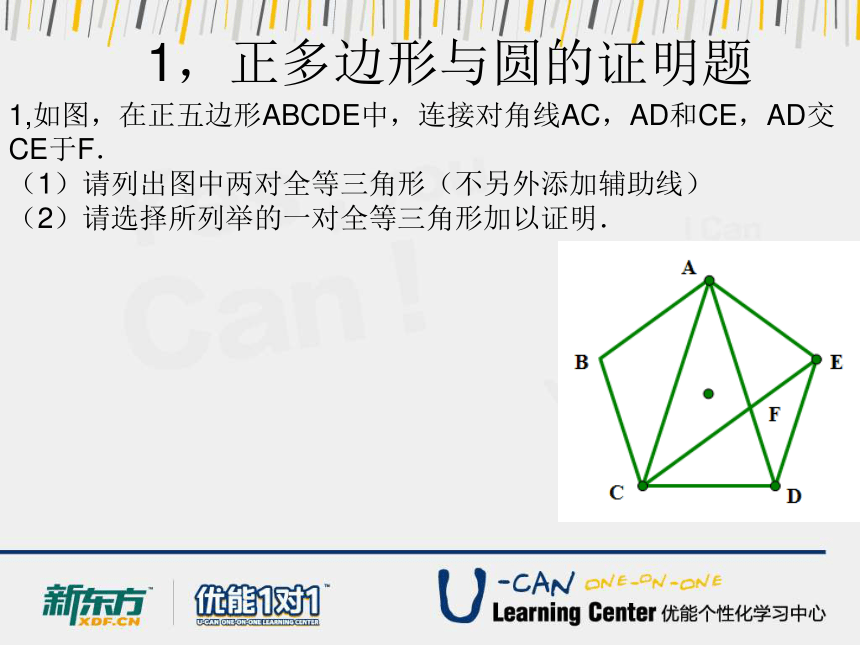
1,如图,在正五边形ABCDE中,连接对角线AC,AD和CE,AD交CE于F.
(1)请列出图中两对全等三角形(不另外添加辅助线)
(2)请选择所列举的一对全等三角形加以证明.
1,主要涉及的考点和技巧
1,正多边形中只有正方形和正五边形的所有对角线是相等的
2,一般的△全等中主要有一下几种判定方法SSS,AAS,ASA
3,切记SSA肯定无法用来判定△全等,右图是一个典型的反例
4,RT△能用HL来判定全等
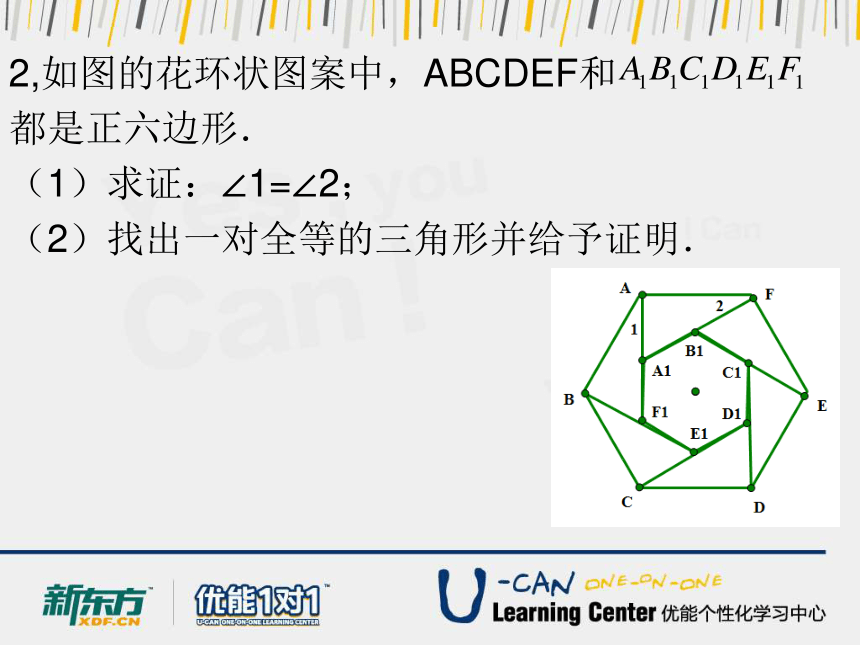
2,如图的花环状图案中,ABCDEF和
都是正六边形.
(1)求证:∠1=∠2;
(2)找出一对全等的三角形并给予证明.
2,主要涉及考点和技巧
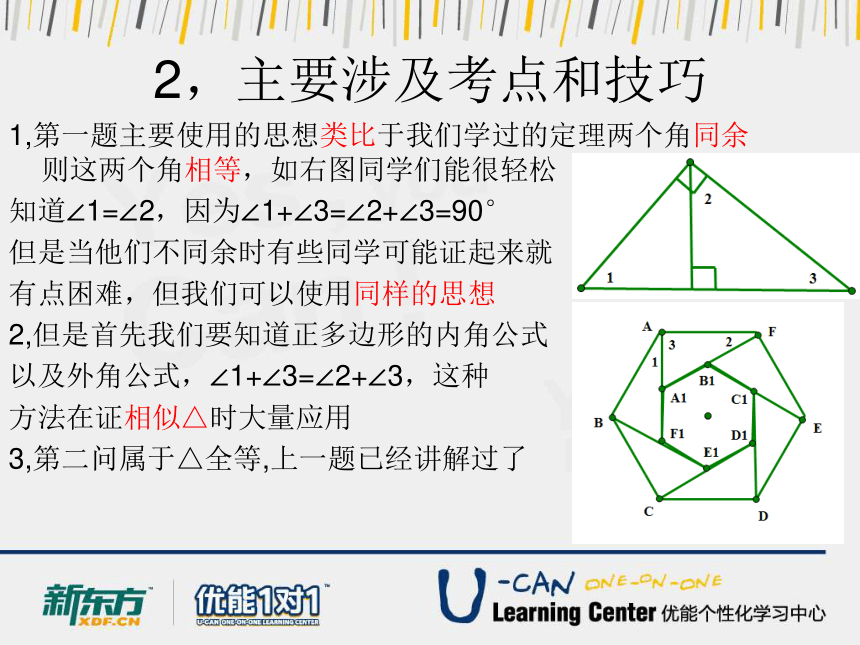
1,第一题主要使用的思想类比于我们学过的定理两个角同余则这两个角相等,如右图同学们能很轻松
知道∠1=∠2,因为∠1+∠3=∠2+∠3=90°
但是当他们不同余时有些同学可能证起来就
有点困难,但我们可以使用同样的思想
2,但是首先我们要知道正多边形的内角公式
以及外角公式,∠1+∠3=∠2+∠3,这种
方法在证相似△时大量应用
3,第二问属于△全等,上一题已经讲解过了
第二题补充练习
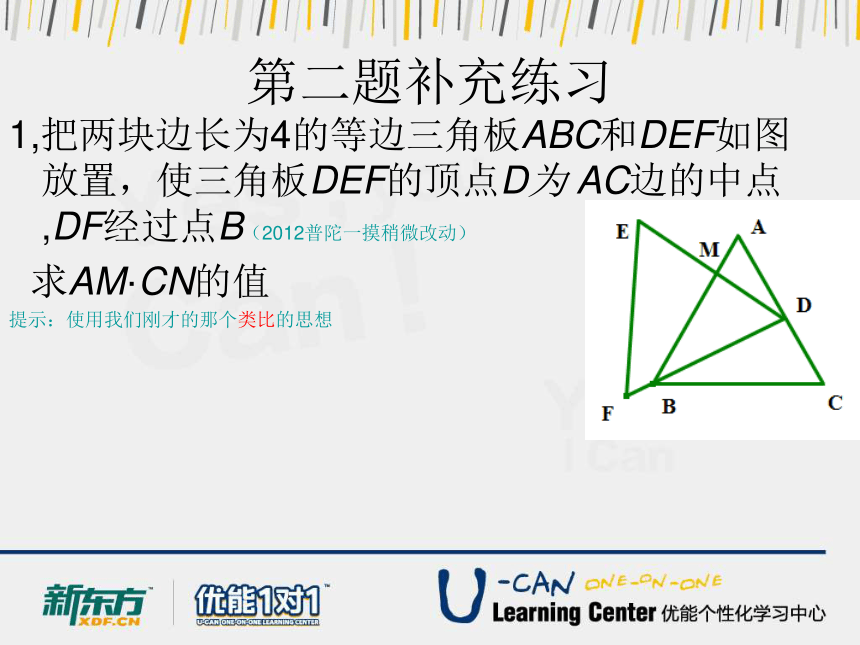
1,把两块边长为4的等边三角板ABC和DEF如图放置,使三角板DEF的顶点D为 AC边的中点,DF经过点B(2012普陀一摸稍微改动)
求AM·CN的值
提示:使用我们刚才的那个类比的思想
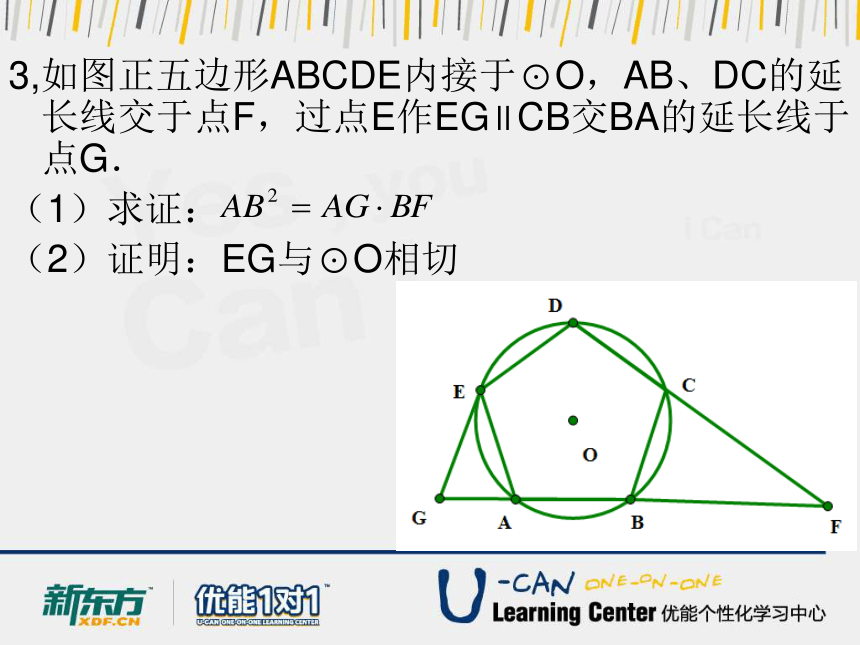
3,如图正五边形ABCDE内接于⊙O,AB、DC的延长线交于点F,过点E作EG∥CB交BA的延长线于点G.
(1)求证:
(2)证明:EG与⊙O相切
3,主要涉及的考点和技巧
1,首先遇到例如 这一类式子,我们应该很快想到很有可能考察的是相似△,很多同学可能会马上急于把他化成比例式子,但是化完后往往会发现无从下手,而正确的方法是先要找一下图形中有没有与上述式子中相等的线段,例如这道题目根据正多边形的性质我们可以得到AB=AE=BC,由此原式可以化为
2, 接着如何把 处理成一个合理的比例式,因为其可以化成 和 两种比例式,尽管这两种比例式都能做,但是有些
同学可能会化完后找不到相应的一对相似△,所以我们推荐使用
因为观察等式左边的字母去掉重复的剩下AEG,同理右边剩下BFC而他们恰恰可以表示两个三角形,而我们的解题方向就能确定了
3,平行线三线八角,同旁内角互补,内错角相等,同位角相等
4,一般相似三角形的判断条件,两边对应成比例且夹角相等或三个内角对应相等
5,RT相似△判断条件,任意一个三角比相等则相似
6,正多边形的半径平分正多边形的内角
7,正多边形的内角和外角公式
8,正多边形的内角和外角公式
9,直线与圆相切时,半径垂直于该直线
4,已知边长为1的正方形ABCD内接于⊙O,延长BC到点E,使CE=BC,连接AE交⊙O于F,求证:EF,FA的长是方程
的两根.
4,主要涉及的考点和技巧
1,尽管题目是一道证明题,但是我们可以把他看成是一道计算题,把EF和FA的长度算出来再代入方程中,看一下是不是其的根就可以得证了
2,在相似△中有两个非常典型的一个是大A型,一个是8字型他们 是最常考察的形似类问题,而此题就是
一个横过来的大A型
3,如何证明两个数时一个一元二次方程的两
个根,方法一:可以分别代入,我们知道
方程的最高次数有几次那就有几个根,相等的根式重根,所以若这两个数都能使一元二次方程成立,那他们就是其的两个根方法二:可以使用韦达定理,有一元二次方程
则有两个数d和e满足d+e= ,de= 则d,e为方程的二个根
1,正多边形与圆的计算题
1,如图,O是正六边形ABCDEF的中心,连接BD、DF、FB,
(1)设△BDF的面积为S1,正六边形ABCDEF的面积为S2,则S1与S2的数量关系是
(2)△ABF通过旋转可与△CBD重合,请指出旋转中心和最小旋转角的度数.
1,主要涉及的考点和技巧
1,我们通常见到的题目是正多边型内接在一个圆中,但很少遇到多边形内接在一个正多边形中,就这一题
而言我们可以看到黄色的三角形由于SAS所以
全部全等,由此可以推出中间那个△是等边△,
对于其他的正多边形我们可以得到同样的结论
但有个条件只有边数≥6且为偶数的正多边形
才会有如此的内接正多边形
2,由于前面我们已经得到DBF是等边△的结论
所以我们要使用三线合一的定理,由于等边△
的特殊性所以容易得到DO=FO=BO=r的结论
由于正六边形的特殊性,我们要记住结论,正六
边形的半径等于边长,由此我们可最后推出右
图六个三角形全部全等
3,旋转的问题中,要合理的找到绕那个点旋转很
多同学也许会拘泥于如何绕点B,其实我们可
以不妨自己动手撕一下草稿纸试一下,就能排
除掉点B是我们所求的点,进而得到合理的旋
转点
2,如图,两正方形彼此相邻且内接于半圆,若小正方形的面积为16,则该半圆的半径为多少?
2,主要涉及的考点和技巧
1,本题的特殊之处是该正多边形是内接
在一个半圆里面的,而本题的难点就在
于如何建立一个合理的方程,在所有这
类多边形与圆的题目中,圆的半径往往
能成为最后的突破口,因为我们能构造
出“半径=半径”的等式,用两种不同的代数式去表示半径,如这题我们可以找到这两个RT△,根据勾股定理,我们可以构造出“半径 =半径 ”的等式,所以问题便能解决了
3,已知多边形ABDEC是由边长为2的等边三角形 ABC和正方形BDEC组成,一圆过A,D,E三点,求该圆半径的长.
3,主要涉及的考点和技巧
1,此题的难点在于题目没有给出圆心在哪里,而只有先找到圆心才能建立合理的方程,在讲这道题目之前先强调一下在中考中尺规作图题里面的一种已知一段弧如何找到圆心,如下图所示,在弧上取两端弦,做中垂线
他们的交点就是圆心
2,这道题我们先要大致的画出圆心的位置
因为AF线段BC下方,由此我们便能
大致的得到圆心O的位置,且
AH⊥BC,AH⊥DE
3,数学的每一个步骤都是有理可据的,所以画完图后有些同学可能会认为四边形ABDO是平行四边形,这是
万万不能胡乱猜测的,我们可以观察到RT△
DOH,而DO是r,DH可以计算出,所以想到
若HO能用含r的代数式表示的话,那就能利用
勾股定理从而建立方程得到半径,进一步观察
得到OH=AH-r=AF+BD-r,而AF可以利用锐角
三角比计算出,从而整个问题引刃而解了
本次学习总结
1, 熟练掌握圆的周长,面积,弧长,圆心角,弦心距,圆与圆的位置关系,线与圆的位置关系,扇形面积,弓形面积,正多边形的定义,对称性,中心,半径,边长,边心距, 内角和,内角,外角,中心角
2,掌握证明题中的一些方法,包括△全等的判定方法,合理的建立相似△的比例,熟知正六边形的半径等于边长等等一些结论
3,掌握计算题中的一些方法,包括如何在内接问题中利用半径以及勾股定理建立合理的一元二次方程等等一些方法
正多边形与圆 的证明以及计算
林佳俊
练习的内容
1,正多边形与圆的证明题
中考模拟题,难题,以及真题
2,正多边形与圆的计算题
中考模拟题,难题,以及真题
1,正多边形与圆的证明题
1,如图,在正五边形ABCDE中,连接对角线AC,AD和CE,AD交CE于F.
(1)请列出图中两对全等三角形(不另外添加辅助线)
(2)请选择所列举的一对全等三角形加以证明.
1,主要涉及的考点和技巧
1,正多边形中只有正方形和正五边形的所有对角线是相等的
2,一般的△全等中主要有一下几种判定方法SSS,AAS,ASA
3,切记SSA肯定无法用来判定△全等,右图是一个典型的反例
4,RT△能用HL来判定全等
2,如图的花环状图案中,ABCDEF和
都是正六边形.
(1)求证:∠1=∠2;
(2)找出一对全等的三角形并给予证明.
2,主要涉及考点和技巧
1,第一题主要使用的思想类比于我们学过的定理两个角同余则这两个角相等,如右图同学们能很轻松
知道∠1=∠2,因为∠1+∠3=∠2+∠3=90°
但是当他们不同余时有些同学可能证起来就
有点困难,但我们可以使用同样的思想
2,但是首先我们要知道正多边形的内角公式
以及外角公式,∠1+∠3=∠2+∠3,这种
方法在证相似△时大量应用
3,第二问属于△全等,上一题已经讲解过了
第二题补充练习
1,把两块边长为4的等边三角板ABC和DEF如图放置,使三角板DEF的顶点D为 AC边的中点,DF经过点B(2012普陀一摸稍微改动)
求AM·CN的值
提示:使用我们刚才的那个类比的思想
3,如图正五边形ABCDE内接于⊙O,AB、DC的延长线交于点F,过点E作EG∥CB交BA的延长线于点G.
(1)求证:
(2)证明:EG与⊙O相切
3,主要涉及的考点和技巧
1,首先遇到例如 这一类式子,我们应该很快想到很有可能考察的是相似△,很多同学可能会马上急于把他化成比例式子,但是化完后往往会发现无从下手,而正确的方法是先要找一下图形中有没有与上述式子中相等的线段,例如这道题目根据正多边形的性质我们可以得到AB=AE=BC,由此原式可以化为
2, 接着如何把 处理成一个合理的比例式,因为其可以化成 和 两种比例式,尽管这两种比例式都能做,但是有些
同学可能会化完后找不到相应的一对相似△,所以我们推荐使用
因为观察等式左边的字母去掉重复的剩下AEG,同理右边剩下BFC而他们恰恰可以表示两个三角形,而我们的解题方向就能确定了
3,平行线三线八角,同旁内角互补,内错角相等,同位角相等
4,一般相似三角形的判断条件,两边对应成比例且夹角相等或三个内角对应相等
5,RT相似△判断条件,任意一个三角比相等则相似
6,正多边形的半径平分正多边形的内角
7,正多边形的内角和外角公式
8,正多边形的内角和外角公式
9,直线与圆相切时,半径垂直于该直线
4,已知边长为1的正方形ABCD内接于⊙O,延长BC到点E,使CE=BC,连接AE交⊙O于F,求证:EF,FA的长是方程
的两根.
4,主要涉及的考点和技巧
1,尽管题目是一道证明题,但是我们可以把他看成是一道计算题,把EF和FA的长度算出来再代入方程中,看一下是不是其的根就可以得证了
2,在相似△中有两个非常典型的一个是大A型,一个是8字型他们 是最常考察的形似类问题,而此题就是
一个横过来的大A型
3,如何证明两个数时一个一元二次方程的两
个根,方法一:可以分别代入,我们知道
方程的最高次数有几次那就有几个根,相等的根式重根,所以若这两个数都能使一元二次方程成立,那他们就是其的两个根方法二:可以使用韦达定理,有一元二次方程
则有两个数d和e满足d+e= ,de= 则d,e为方程的二个根
1,正多边形与圆的计算题
1,如图,O是正六边形ABCDEF的中心,连接BD、DF、FB,
(1)设△BDF的面积为S1,正六边形ABCDEF的面积为S2,则S1与S2的数量关系是
(2)△ABF通过旋转可与△CBD重合,请指出旋转中心和最小旋转角的度数.
1,主要涉及的考点和技巧
1,我们通常见到的题目是正多边型内接在一个圆中,但很少遇到多边形内接在一个正多边形中,就这一题
而言我们可以看到黄色的三角形由于SAS所以
全部全等,由此可以推出中间那个△是等边△,
对于其他的正多边形我们可以得到同样的结论
但有个条件只有边数≥6且为偶数的正多边形
才会有如此的内接正多边形
2,由于前面我们已经得到DBF是等边△的结论
所以我们要使用三线合一的定理,由于等边△
的特殊性所以容易得到DO=FO=BO=r的结论
由于正六边形的特殊性,我们要记住结论,正六
边形的半径等于边长,由此我们可最后推出右
图六个三角形全部全等
3,旋转的问题中,要合理的找到绕那个点旋转很
多同学也许会拘泥于如何绕点B,其实我们可
以不妨自己动手撕一下草稿纸试一下,就能排
除掉点B是我们所求的点,进而得到合理的旋
转点
2,如图,两正方形彼此相邻且内接于半圆,若小正方形的面积为16,则该半圆的半径为多少?
2,主要涉及的考点和技巧
1,本题的特殊之处是该正多边形是内接
在一个半圆里面的,而本题的难点就在
于如何建立一个合理的方程,在所有这
类多边形与圆的题目中,圆的半径往往
能成为最后的突破口,因为我们能构造
出“半径=半径”的等式,用两种不同的代数式去表示半径,如这题我们可以找到这两个RT△,根据勾股定理,我们可以构造出“半径 =半径 ”的等式,所以问题便能解决了
3,已知多边形ABDEC是由边长为2的等边三角形 ABC和正方形BDEC组成,一圆过A,D,E三点,求该圆半径的长.
3,主要涉及的考点和技巧
1,此题的难点在于题目没有给出圆心在哪里,而只有先找到圆心才能建立合理的方程,在讲这道题目之前先强调一下在中考中尺规作图题里面的一种已知一段弧如何找到圆心,如下图所示,在弧上取两端弦,做中垂线
他们的交点就是圆心
2,这道题我们先要大致的画出圆心的位置
因为AF
大致的得到圆心O的位置,且
AH⊥BC,AH⊥DE
3,数学的每一个步骤都是有理可据的,所以画完图后有些同学可能会认为四边形ABDO是平行四边形,这是
万万不能胡乱猜测的,我们可以观察到RT△
DOH,而DO是r,DH可以计算出,所以想到
若HO能用含r的代数式表示的话,那就能利用
勾股定理从而建立方程得到半径,进一步观察
得到OH=AH-r=AF+BD-r,而AF可以利用锐角
三角比计算出,从而整个问题引刃而解了
本次学习总结
1, 熟练掌握圆的周长,面积,弧长,圆心角,弦心距,圆与圆的位置关系,线与圆的位置关系,扇形面积,弓形面积,正多边形的定义,对称性,中心,半径,边长,边心距, 内角和,内角,外角,中心角
2,掌握证明题中的一些方法,包括△全等的判定方法,合理的建立相似△的比例,熟知正六边形的半径等于边长等等一些结论
3,掌握计算题中的一些方法,包括如何在内接问题中利用半径以及勾股定理建立合理的一元二次方程等等一些方法
