2021-2022学年人教版八年级数学上册 13.2画轴对称图形 课后练习 (word版含答案)
文档属性
| 名称 | 2021-2022学年人教版八年级数学上册 13.2画轴对称图形 课后练习 (word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 414.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-27 17:57:15 | ||
图片预览




文档简介
2021——2022学年度人教版八年级数学上册 第十三章轴对称 13.2画轴对称图形 课后练习
一、选择题
1.下列图形中,对称轴条数最少的是( )
A. B. C. D.
2.如图,在小正三角形组成的网格中,已有6个小正三角形涂黑,还需涂黑2个小正三角形,使它们与原来涂黑的小正三角形组成的新图案恰为轴对称图形,则填涂的方案有( )种.
A.3 B.4 C.5 D.6
3.如图,在平面直角坐标系中,对进行循环往复的轴对称变换,若原来点A坐标是,则经过第2021次变换后点A的对应点的坐标为( )
A. B. C. D.
4.如图,在4×4的正方形网格中,已将图中的三个小正方形涂上阴影,若再将图中其余小正方形任选一个也涂上阴影,使得整个阴影部分是轴对称图形,那么符合条件的小正方形共有( )
A. B.5个 C.4个 D.3个
5.已知中,与关于轴对称,与关于轴对称,与关于轴对称,与关于轴对称……,如果在第二象限,那么在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6.已知点A的坐标为,点B的坐标为,将线段沿坐标轴翻折180°后,若点A的对应点的坐标为,则点B的对应点的坐标为( )
A. B. C. D.
7.平面直角坐标系中,点A(3,2)与点B关于y轴对称,则点B的坐标为( )
A.(3,-2) B.(-3,-2) C.(-3,2) D.(-2,3)
8.如图,在锐角△ABC中,AB=6,∠ABC=60°,∠ABC的平分线交AC于点D,点P,Q分别是BD,AB上的动点,则AP+PQ的最小值为( )
A.6 B.6 C.3 D.3
9.如图,,C为OB上的定点,M,N分别为射线OA、OB上的动点.当的值最小时,的度数为( )
A. B. C. D.
10.如图,中,,,,于点,是的垂直平分线,交于点,交于点,在上确定一点,使最小,则这个最小值为( )
A.3.5 B.4 C.4.5 D.5
二、填空题
11.如图,在长方形ABCD中,AD=BC=5,AB=CD=12,AC=13,动点M在线段AC上运动(不与端点重合),点M关于边AD,DC的对称点分别为M1,M2,连接M1M2,点D在M1M2上,则在点M的运动过程中,线段M1M2长度的最小值是_______.
12.已知中,垂直平分交于F,垂足为E,若,则_______.
13.规定:在平面直角坐标系中,“把某一图形先沿x轴翻折,再沿y轴翻折”为一次变换.如图,已知正方形,顶点,若正方形经过一次上述变换,则点A变换后的坐标为________;对正方形连续做2021次这样的变换,则点D变换后的坐标为_________.
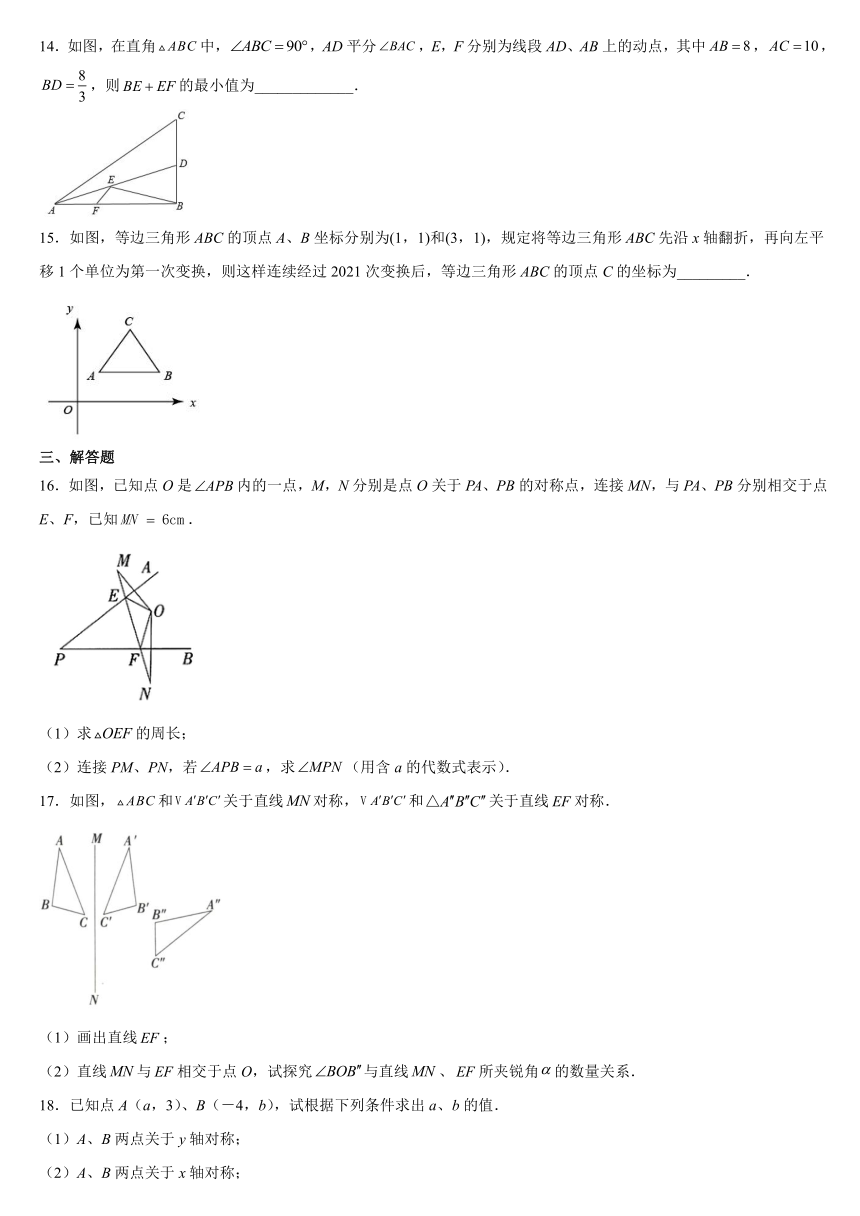
14.如图,在直角中,,AD平分,E,F分别为线段AD、AB上的动点,其中,,,则的最小值为_____________.
15.如图,等边三角形ABC的顶点A、B坐标分别为(1,1)和(3,1),规定将等边三角形ABC先沿x轴翻折,再向左平移1个单位为第一次变换,则这样连续经过2021次变换后,等边三角形ABC的顶点C的坐标为_________.
三、解答题
16.如图,已知点O是内的一点,M,N分别是点O关于PA、PB的对称点,连接MN,与PA、PB分别相交于点E、F,已知.
(1)求的周长;
(2)连接PM、PN,若,求(用含a的代数式表示).
17.如图,和关于直线对称,和关于直线对称.
(1)画出直线;
(2)直线与相交于点O,试探究与直线、所夹锐角的数量关系.
18.已知点A(a,3)、B(-4,b),试根据下列条件求出a、b的值.
(1)A、B两点关于y轴对称;
(2)A、B两点关于x轴对称;
(3)AB∥x轴;
(4)A、B两点在第二、四象限两坐标轴夹角的平分线上.
19.如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC和△DEF(顶点为网格线的交点),以及过格点的直线l.
(1)将△ABC向右平移3个单位长度,再向下平移4个单位长度,画出平移后的三角形;
(2)画出△DEF关于直线l对称的三角形;
(3)填空:∠C+∠F= .
20.在一张半透明的纸的左边画上一个三角形,把这张纸对折后描图,打开这张纸,就能得到相应的另外一个三角形.如图所示:
(1)这两个三角形有什么关系?
(2)这条折痕和这两个三角形有什么关系?
(3)图中的点A和点D之间的连线和折痕有什么关系?
21.如图1,在中,,,,.点为边上的一个动点,过点作于点,求的最小值.请你在横线上补充其推理过程或理由.
解:如图2,延长到点,使得,连接,
因为(已知),
所以____________________(垂直的定义),
所以____________________(线段垂直平分线的性质),
所以(等式性质),
所以过点作于点,交于点,此时取最小值,连接.
在和中,
因为,,____________________,
所以(理由:____________________),
所以(全等三角形面积相等),
因为,
又因为,
所以____________________(同一三角形面积相等),
所以,
所以______________________________.
22.如图,在中,,D为的中点,E为延长线上一点,连接,过点D作,交的延长线于点F,连接.作点B关于直线的对称点G,连接.
(1)依题意补全图形;
(2)若.
①求的度数(用含的式子表示);
②请判断以线段为边的三角形的形状,并说明理由.
23.如图,直线l1∥l2,直线l3交直线l1于点B,交直线l2于点D,O是线段BD的中点.过点B作BA⊥l2于点A,过点D作DC⊥l1于点C,E是线段BD上一动点(不与点B,D重合),点E关于直线AB,AD的对称点分别为P,Q,射线PO与射线QD相交于点N,连接PQ.
(1)求证:点A是PQ的中点;
(2)请判断线段QN与线段BD是否相等,并说明理由.
【参考答案】
1.A 2.D 3.C 4.B 5.A 6.C 7.C 8.D 9.B 10.B
11.
12.12
13.
14.
15.(﹣2019,﹣﹣1).
16.解:(1)∵M,N分别是点O关于PA、PB的对称点,∴,,
∴的周长;
(2)如答案图,连接OP,
∵M,N分别是点O关于PA、PB的对称点,
∴,,∴.
17.解:(1)如图,连接.
作线段的垂直平分线.
则直线是和的对称轴;
(2)如图,连接.
∵和关于直线对称,
∴.
又∵和关于直线对称,∴.
∴,
即.
18.解:(1)A、B两点关于y轴对称,
故有b=3,a=4;
(2)A、B两点关于x轴对称;
所以有a=-4,b=-3;
(3)AB∥x轴,
即b=3,a为≠-4的任意实数.
(4)如图,
根据题意,a+3=0;
b-4=0;
所以a=-3,b=4.
19.
(1)如图,△A'B'C' 即为所求.
(2)如图,△A'D'F' 即为所求.
(3)由图可得,∠C+∠F=90°.
故答案为:90°
20.(1)这两个三角形的形状、大小完全相同;(2)两个三角形关于折痕成轴对称;(3)两点的连线,被折痕垂直平分
21.解:如图2,延长BC到点B′,使得BC=B′C,连接PB′,
因为∠ACB=90°(已知),
所以 AC⊥BB'(垂直的定义),
所以PB=PB'(线段垂直平分线的性质),
所以PB+PD=PB′+PD(等式性质),
所以过点B′作B′D⊥AB于点D,交AC于点P,此时PB+PD取最小值,连接AB′.
在△ABC和△AB′C中,
因为∠ACB=∠ACB′=90°,AC=AC,BC=B′C,
所以△ABC≌△AB′C(理由:SAS),
所以S△ABB′=S△ABC+S△AB'C=2S△ABC(全等三角形面积相等),
因为S△ABB′===
又因为S△ABB′=2S△ABC=2××BC×AC=2××6×8=48
所以(同一三角形面积相等),
所以B′D=
所以 PB+PD的最小值为.
故答案为:;;;;;;的最小值是.
22.解:(1)补全图形,如图所示,
(2)①∵,∴,
由轴对称性质可知,,
∵,∴,
∴,
②以线段为边的三角形是直角三角形,
如图,连接,
由轴对称性质可知,,
∵D是的中点,∴,
∵,∴,
∵,
∴,∴,
∵,∴,
∴,
∴以线段为边的三角形是直角三角形,
∴以线段为边的三角形是直角三角形.
23.解:(1)连接AE,PE,QE,如图
∵点E关于直线AB,AD的对称点分别为P,Q
∴AP=AE,AQ=AE,∠1=∠2,∠3=∠4,
∴AP=AQ
∵AB⊥l2,
∴∠2+∠3=90°
∴∠1+∠2+∠3+∠4=180°
∴P,A,Q三点在同一条直线上
∴点A是PQ的中点.
(2)QN=BD,理由如下:连接PB
∵点E关于直线AB,AD的对称点分别为P,Q
∴BP=BE,DQ=DE,∠5=∠6,∠7=∠8
∵l1//l2,DC⊥l1,
∴DC⊥l2,
∴∠7+∠9=90°,
∴∠8+∠10=90°,
∴∠9=∠10
又∵AB⊥l2,DC⊥l2,
∴AB//CD
∴∠6=∠9,
∴∠5+∠6=∠9+∠10
即∠OBP=∠ODN
∵O是线段BD的中点,
∴OB=OD
在△BOP和△DON中
∴△BOP≌△DON
∴BP=DN,
∴BE=DN
∴QN=DQ+DN=DE+BE=BD
一、选择题
1.下列图形中,对称轴条数最少的是( )
A. B. C. D.
2.如图,在小正三角形组成的网格中,已有6个小正三角形涂黑,还需涂黑2个小正三角形,使它们与原来涂黑的小正三角形组成的新图案恰为轴对称图形,则填涂的方案有( )种.
A.3 B.4 C.5 D.6
3.如图,在平面直角坐标系中,对进行循环往复的轴对称变换,若原来点A坐标是,则经过第2021次变换后点A的对应点的坐标为( )
A. B. C. D.
4.如图,在4×4的正方形网格中,已将图中的三个小正方形涂上阴影,若再将图中其余小正方形任选一个也涂上阴影,使得整个阴影部分是轴对称图形,那么符合条件的小正方形共有( )
A. B.5个 C.4个 D.3个
5.已知中,与关于轴对称,与关于轴对称,与关于轴对称,与关于轴对称……,如果在第二象限,那么在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6.已知点A的坐标为,点B的坐标为,将线段沿坐标轴翻折180°后,若点A的对应点的坐标为,则点B的对应点的坐标为( )
A. B. C. D.
7.平面直角坐标系中,点A(3,2)与点B关于y轴对称,则点B的坐标为( )
A.(3,-2) B.(-3,-2) C.(-3,2) D.(-2,3)
8.如图,在锐角△ABC中,AB=6,∠ABC=60°,∠ABC的平分线交AC于点D,点P,Q分别是BD,AB上的动点,则AP+PQ的最小值为( )
A.6 B.6 C.3 D.3
9.如图,,C为OB上的定点,M,N分别为射线OA、OB上的动点.当的值最小时,的度数为( )
A. B. C. D.
10.如图,中,,,,于点,是的垂直平分线,交于点,交于点,在上确定一点,使最小,则这个最小值为( )
A.3.5 B.4 C.4.5 D.5
二、填空题
11.如图,在长方形ABCD中,AD=BC=5,AB=CD=12,AC=13,动点M在线段AC上运动(不与端点重合),点M关于边AD,DC的对称点分别为M1,M2,连接M1M2,点D在M1M2上,则在点M的运动过程中,线段M1M2长度的最小值是_______.
12.已知中,垂直平分交于F,垂足为E,若,则_______.
13.规定:在平面直角坐标系中,“把某一图形先沿x轴翻折,再沿y轴翻折”为一次变换.如图,已知正方形,顶点,若正方形经过一次上述变换,则点A变换后的坐标为________;对正方形连续做2021次这样的变换,则点D变换后的坐标为_________.
14.如图,在直角中,,AD平分,E,F分别为线段AD、AB上的动点,其中,,,则的最小值为_____________.
15.如图,等边三角形ABC的顶点A、B坐标分别为(1,1)和(3,1),规定将等边三角形ABC先沿x轴翻折,再向左平移1个单位为第一次变换,则这样连续经过2021次变换后,等边三角形ABC的顶点C的坐标为_________.
三、解答题
16.如图,已知点O是内的一点,M,N分别是点O关于PA、PB的对称点,连接MN,与PA、PB分别相交于点E、F,已知.
(1)求的周长;
(2)连接PM、PN,若,求(用含a的代数式表示).
17.如图,和关于直线对称,和关于直线对称.
(1)画出直线;
(2)直线与相交于点O,试探究与直线、所夹锐角的数量关系.
18.已知点A(a,3)、B(-4,b),试根据下列条件求出a、b的值.
(1)A、B两点关于y轴对称;
(2)A、B两点关于x轴对称;
(3)AB∥x轴;
(4)A、B两点在第二、四象限两坐标轴夹角的平分线上.
19.如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC和△DEF(顶点为网格线的交点),以及过格点的直线l.
(1)将△ABC向右平移3个单位长度,再向下平移4个单位长度,画出平移后的三角形;
(2)画出△DEF关于直线l对称的三角形;
(3)填空:∠C+∠F= .
20.在一张半透明的纸的左边画上一个三角形,把这张纸对折后描图,打开这张纸,就能得到相应的另外一个三角形.如图所示:
(1)这两个三角形有什么关系?
(2)这条折痕和这两个三角形有什么关系?
(3)图中的点A和点D之间的连线和折痕有什么关系?
21.如图1,在中,,,,.点为边上的一个动点,过点作于点,求的最小值.请你在横线上补充其推理过程或理由.
解:如图2,延长到点,使得,连接,
因为(已知),
所以____________________(垂直的定义),
所以____________________(线段垂直平分线的性质),
所以(等式性质),
所以过点作于点,交于点,此时取最小值,连接.
在和中,
因为,,____________________,
所以(理由:____________________),
所以(全等三角形面积相等),
因为,
又因为,
所以____________________(同一三角形面积相等),
所以,
所以______________________________.
22.如图,在中,,D为的中点,E为延长线上一点,连接,过点D作,交的延长线于点F,连接.作点B关于直线的对称点G,连接.
(1)依题意补全图形;
(2)若.
①求的度数(用含的式子表示);
②请判断以线段为边的三角形的形状,并说明理由.
23.如图,直线l1∥l2,直线l3交直线l1于点B,交直线l2于点D,O是线段BD的中点.过点B作BA⊥l2于点A,过点D作DC⊥l1于点C,E是线段BD上一动点(不与点B,D重合),点E关于直线AB,AD的对称点分别为P,Q,射线PO与射线QD相交于点N,连接PQ.
(1)求证:点A是PQ的中点;
(2)请判断线段QN与线段BD是否相等,并说明理由.
【参考答案】
1.A 2.D 3.C 4.B 5.A 6.C 7.C 8.D 9.B 10.B
11.
12.12
13.
14.
15.(﹣2019,﹣﹣1).
16.解:(1)∵M,N分别是点O关于PA、PB的对称点,∴,,
∴的周长;
(2)如答案图,连接OP,
∵M,N分别是点O关于PA、PB的对称点,
∴,,∴.
17.解:(1)如图,连接.
作线段的垂直平分线.
则直线是和的对称轴;
(2)如图,连接.
∵和关于直线对称,
∴.
又∵和关于直线对称,∴.
∴,
即.
18.解:(1)A、B两点关于y轴对称,
故有b=3,a=4;
(2)A、B两点关于x轴对称;
所以有a=-4,b=-3;
(3)AB∥x轴,
即b=3,a为≠-4的任意实数.
(4)如图,
根据题意,a+3=0;
b-4=0;
所以a=-3,b=4.
19.
(1)如图,△A'B'C' 即为所求.
(2)如图,△A'D'F' 即为所求.
(3)由图可得,∠C+∠F=90°.
故答案为:90°
20.(1)这两个三角形的形状、大小完全相同;(2)两个三角形关于折痕成轴对称;(3)两点的连线,被折痕垂直平分
21.解:如图2,延长BC到点B′,使得BC=B′C,连接PB′,
因为∠ACB=90°(已知),
所以 AC⊥BB'(垂直的定义),
所以PB=PB'(线段垂直平分线的性质),
所以PB+PD=PB′+PD(等式性质),
所以过点B′作B′D⊥AB于点D,交AC于点P,此时PB+PD取最小值,连接AB′.
在△ABC和△AB′C中,
因为∠ACB=∠ACB′=90°,AC=AC,BC=B′C,
所以△ABC≌△AB′C(理由:SAS),
所以S△ABB′=S△ABC+S△AB'C=2S△ABC(全等三角形面积相等),
因为S△ABB′===
又因为S△ABB′=2S△ABC=2××BC×AC=2××6×8=48
所以(同一三角形面积相等),
所以B′D=
所以 PB+PD的最小值为.
故答案为:;;;;;;的最小值是.
22.解:(1)补全图形,如图所示,
(2)①∵,∴,
由轴对称性质可知,,
∵,∴,
∴,
②以线段为边的三角形是直角三角形,
如图,连接,
由轴对称性质可知,,
∵D是的中点,∴,
∵,∴,
∵,
∴,∴,
∵,∴,
∴,
∴以线段为边的三角形是直角三角形,
∴以线段为边的三角形是直角三角形.
23.解:(1)连接AE,PE,QE,如图
∵点E关于直线AB,AD的对称点分别为P,Q
∴AP=AE,AQ=AE,∠1=∠2,∠3=∠4,
∴AP=AQ
∵AB⊥l2,
∴∠2+∠3=90°
∴∠1+∠2+∠3+∠4=180°
∴P,A,Q三点在同一条直线上
∴点A是PQ的中点.
(2)QN=BD,理由如下:连接PB
∵点E关于直线AB,AD的对称点分别为P,Q
∴BP=BE,DQ=DE,∠5=∠6,∠7=∠8
∵l1//l2,DC⊥l1,
∴DC⊥l2,
∴∠7+∠9=90°,
∴∠8+∠10=90°,
∴∠9=∠10
又∵AB⊥l2,DC⊥l2,
∴AB//CD
∴∠6=∠9,
∴∠5+∠6=∠9+∠10
即∠OBP=∠ODN
∵O是线段BD的中点,
∴OB=OD
在△BOP和△DON中
∴△BOP≌△DON
∴BP=DN,
∴BE=DN
∴QN=DQ+DN=DE+BE=BD
