北师大版数学九年级下二次函数—— 何时获得最大利润
文档属性
| 名称 | 北师大版数学九年级下二次函数—— 何时获得最大利润 |  | |
| 格式 | zip | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-08-31 22:36:49 | ||
图片预览






文档简介
(共20张PPT)
北师大版数学教材九年级下册
第二章 二次函数
2 . 抛物线y=ax2+bx+c对称轴是 ,顶
点坐标是 .
复习巩固
1. 抛物线y=a(x-h)2+k的对称轴是 ,顶点坐标是 .
直线x=h
(h,k)
3.二次函数y = - x2 + 2x – 3开口方向___________.
顶点坐标 ___________
当x= 时,函数y有最 值,
即y 最 值= 。
1
大
- 2
大
向下
(1,-2)
某果园有100棵橙子树,每一棵树平均结600个橙子。现准备多种一些橙子树以提高产量,但是如果多种树,那么树之间的距离和每一棵树所接受的阳光就会减少。根据经验估计,每多种一棵树,平均每棵树就会少结5个橙子。
(1) 假设果园增种x棵橙子树,那么果园共有___________棵橙子树,这时平均每棵树结___________个橙子.
增种多少棵橙子树,才能使橙子的总产量最高?
(100+x)
(600-5x)
y=(100+x)(600-5x)=-5x +100x+60000.
回顾与思考
何时橙子产量最大
(2)如果果园橙子的总产量为y个,那么y与x之间的关系式是:
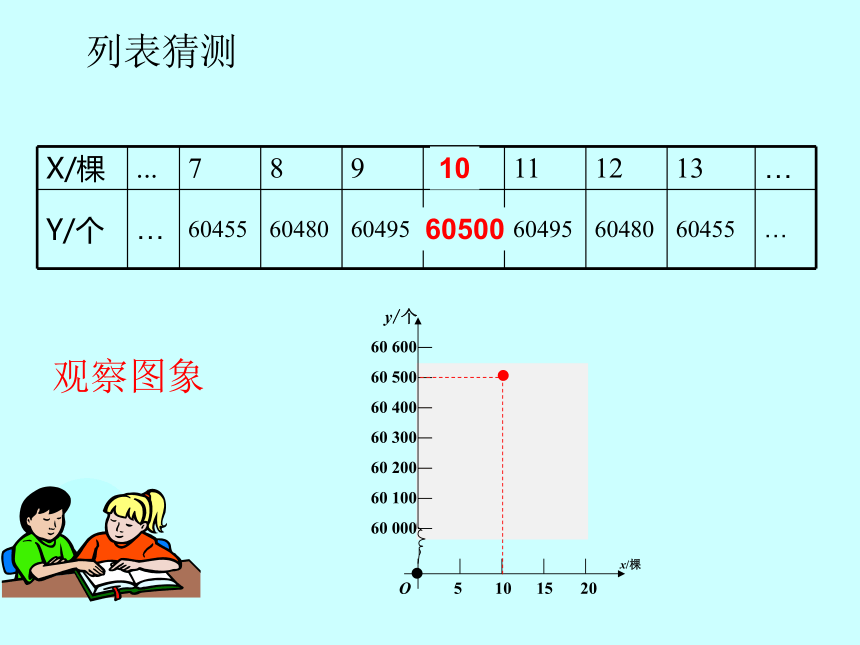
列表猜测
X/棵 ... 7 8 9 10 11 12 13 …
Y/个 … 60455 60480 60495 60500 60495 60480 60455 …
O
5
10
15
20
60 000
60 100
60 200
60 300
60 400
60 500
60 600
x/棵
y/个
观察图象
10
60500
解:
∵当x=10时,y最大=60500
∴增种10棵树时, 总产量最大,是60500个
y=(600-5x)(100+x )
=-5x +100x+60000
=-5(x-10)2+60500
何时橙子总产量最大
例 某商场销售一种T恤衫,每件进价是20元.每件售价为40元时,每天售出200件.经调查,销售单价每降低1元,每天就会多售出20件.销售单价为多少时,每天总利润最多?最多是多少?
问题:1、在上述问题当中主要考虑哪两个变量?哪个变
量随哪个变量的变化而变化?即自变量是哪个量?
因变量是哪个量?
2、若设销售单价为x元,
则单件利润可表示为 元。
销售量可表示为_______________件。
总利润可表示为________________________元。
3、若设总利润为y元,你能写出y与x关系式吗?
(X-20)
[200+20(40-x)]
(x-20)[200+20(40-x)]
何时获得最大利润
探求新知
若设每件降价x元
则单件利润可表示为 元
销售量可表示为____________________件
总利润为________________________元
设总利润为y元,你能写出y与x的关系式吗?
请你求出售价为多少时获总利最大?最大是多少?
(40-x-20)
(200+20x)
y =(40-x-20)(200+20x)
某商场销售一种T恤衫,每件进价是20元.每件售价为40元时,每天售出200件.经调查,销售单价每降低1元,每天就会多售出20件.销售单价为多少时,每天获总利最多?最多是多少?
何时获得最大利润
探求新知
(40-x-20)(200+20x)
解:设每件降价x元,总利润为y元
y =(40-x-20)(200+20x)
=-20x2+200x+4000
=-20(x-5)2+4500
∴当x=5时,y 的最大值为4500
∴当销售单价为35元时,获利最大为4500元。
解析问题
2a
b
-40
200
-
=-
=5
4a
4ac-b2
=4500
总结深化
解题步骤:
1、审题:设出两个变量
2、分析变量之间的关系写出二次函数关系式
3、确定顶点坐标求出最值
4、根据要求合理作答
何时获得最大利润
巩固练习
某商贩将进价为8元的商品按每件10元销售,每天可售出100件.他想采用提高售价的办法来增加利润.经试验发现,这种商品每件每提价1元,每天的销售量就会减少10件.每件售价多少元时,才能使一天的利润最大 最大是多少?
解:设每件售价为x元,一天的利润为y元
巩固练习
某商贩将进价为8元的商品按每件10元销售,每天可售出100件.他想采用提高售价的办法来增加利润.经试验发现,这种商品每件每提价1元,每天的销售量就会减少10件.每件售价多少元时,才能使一天的利润最大
当x=14时,利润最大,是360元
何时获得最大利润
解:设每件售价提高x元,一天的利润为y元
巩固练习
某商贩将进价为8元的商品按每件10元销售,每天可售出100件.他想采用提高售价的办法来增加利润.经试验发现,这种商品每件每提价1元,每天的销售量就会减少10件.每件售价多少元时,才能使一天的利润最大
y=(10+x-8)(100-10x)
=(2+x)(100-10x)
=-10x2+80x+200
=-10(x-4)2+360
当x=4时,即售价为14元时,利润最大360元。
何时获得最大利润
西瓜经营户以2元/千克的价格购进一批小型西瓜,以3元/千克的价格出售,每天可售出200千克,为了促销,该经营户决定降价销售,经调查发现,这种小型西瓜每降价0.1元/千克,每天可多售出40千克,另外,每天要支出房租等费用共24元。当每千克西瓜售价降低多少元时每天盈利最大?
则每千克西瓜利润为_______元
销售量可表示为____________千克
每天的盈利y与x关系式为______________________
拓展延伸
(3-x-2)
(200+400x)
y=(3-x-2)(200+400x)-24
何时获得最大利润
若设每千克西瓜的售价降低x元,每天盈利y元。
设出变量
变量关系
二次函数关系式
顶点坐标
函数的最值
解释
分析
确定
合理
解关于二次函数最值的应用题的一般思路:
求出
写出
收获与感悟
家佳源购进一批单价为20元的日用品,如果以单价30元销售,那么半个月内可以售出400件。根据销售经验,提高单价会导致销售量的减少,即销售单价每提高1元,销售量相应减少20件。如何提高售价,才能在半个月内获得最大利润?最大利润是多少?
达标检测
何时获得最大利润
解:设每件售价提高x元,半月所获利润为y元
y=(30+x-20)(400-20x)
=(10+x)(400-20x)
=-20x2+200x+4000
x=-200/-40=5
由x=5得y=(30+5-20)(400-20×5)=4500
答:当每件售价提高5元时,最大利润为4500元。
课堂寄语
二次函数是一类最优化问题的数学模型,能指导我们解决生活中的实际问题,同学们,认真学习数学吧,因为数学来源于生活,更能优化我们的生活。
布置作业,完善提升
课本65页随堂练习1,课本66页1、2
北师大版数学教材九年级下册
第二章 二次函数
2 . 抛物线y=ax2+bx+c对称轴是 ,顶
点坐标是 .
复习巩固
1. 抛物线y=a(x-h)2+k的对称轴是 ,顶点坐标是 .
直线x=h
(h,k)
3.二次函数y = - x2 + 2x – 3开口方向___________.
顶点坐标 ___________
当x= 时,函数y有最 值,
即y 最 值= 。
1
大
- 2
大
向下
(1,-2)
某果园有100棵橙子树,每一棵树平均结600个橙子。现准备多种一些橙子树以提高产量,但是如果多种树,那么树之间的距离和每一棵树所接受的阳光就会减少。根据经验估计,每多种一棵树,平均每棵树就会少结5个橙子。
(1) 假设果园增种x棵橙子树,那么果园共有___________棵橙子树,这时平均每棵树结___________个橙子.
增种多少棵橙子树,才能使橙子的总产量最高?
(100+x)
(600-5x)
y=(100+x)(600-5x)=-5x +100x+60000.
回顾与思考
何时橙子产量最大
(2)如果果园橙子的总产量为y个,那么y与x之间的关系式是:
列表猜测
X/棵 ... 7 8 9 10 11 12 13 …
Y/个 … 60455 60480 60495 60500 60495 60480 60455 …
O
5
10
15
20
60 000
60 100
60 200
60 300
60 400
60 500
60 600
x/棵
y/个
观察图象
10
60500
解:
∵当x=10时,y最大=60500
∴增种10棵树时, 总产量最大,是60500个
y=(600-5x)(100+x )
=-5x +100x+60000
=-5(x-10)2+60500
何时橙子总产量最大
例 某商场销售一种T恤衫,每件进价是20元.每件售价为40元时,每天售出200件.经调查,销售单价每降低1元,每天就会多售出20件.销售单价为多少时,每天总利润最多?最多是多少?
问题:1、在上述问题当中主要考虑哪两个变量?哪个变
量随哪个变量的变化而变化?即自变量是哪个量?
因变量是哪个量?
2、若设销售单价为x元,
则单件利润可表示为 元。
销售量可表示为_______________件。
总利润可表示为________________________元。
3、若设总利润为y元,你能写出y与x关系式吗?
(X-20)
[200+20(40-x)]
(x-20)[200+20(40-x)]
何时获得最大利润
探求新知
若设每件降价x元
则单件利润可表示为 元
销售量可表示为____________________件
总利润为________________________元
设总利润为y元,你能写出y与x的关系式吗?
请你求出售价为多少时获总利最大?最大是多少?
(40-x-20)
(200+20x)
y =(40-x-20)(200+20x)
某商场销售一种T恤衫,每件进价是20元.每件售价为40元时,每天售出200件.经调查,销售单价每降低1元,每天就会多售出20件.销售单价为多少时,每天获总利最多?最多是多少?
何时获得最大利润
探求新知
(40-x-20)(200+20x)
解:设每件降价x元,总利润为y元
y =(40-x-20)(200+20x)
=-20x2+200x+4000
=-20(x-5)2+4500
∴当x=5时,y 的最大值为4500
∴当销售单价为35元时,获利最大为4500元。
解析问题
2a
b
-40
200
-
=-
=5
4a
4ac-b2
=4500
总结深化
解题步骤:
1、审题:设出两个变量
2、分析变量之间的关系写出二次函数关系式
3、确定顶点坐标求出最值
4、根据要求合理作答
何时获得最大利润
巩固练习
某商贩将进价为8元的商品按每件10元销售,每天可售出100件.他想采用提高售价的办法来增加利润.经试验发现,这种商品每件每提价1元,每天的销售量就会减少10件.每件售价多少元时,才能使一天的利润最大 最大是多少?
解:设每件售价为x元,一天的利润为y元
巩固练习
某商贩将进价为8元的商品按每件10元销售,每天可售出100件.他想采用提高售价的办法来增加利润.经试验发现,这种商品每件每提价1元,每天的销售量就会减少10件.每件售价多少元时,才能使一天的利润最大
当x=14时,利润最大,是360元
何时获得最大利润
解:设每件售价提高x元,一天的利润为y元
巩固练习
某商贩将进价为8元的商品按每件10元销售,每天可售出100件.他想采用提高售价的办法来增加利润.经试验发现,这种商品每件每提价1元,每天的销售量就会减少10件.每件售价多少元时,才能使一天的利润最大
y=(10+x-8)(100-10x)
=(2+x)(100-10x)
=-10x2+80x+200
=-10(x-4)2+360
当x=4时,即售价为14元时,利润最大360元。
何时获得最大利润
西瓜经营户以2元/千克的价格购进一批小型西瓜,以3元/千克的价格出售,每天可售出200千克,为了促销,该经营户决定降价销售,经调查发现,这种小型西瓜每降价0.1元/千克,每天可多售出40千克,另外,每天要支出房租等费用共24元。当每千克西瓜售价降低多少元时每天盈利最大?
则每千克西瓜利润为_______元
销售量可表示为____________千克
每天的盈利y与x关系式为______________________
拓展延伸
(3-x-2)
(200+400x)
y=(3-x-2)(200+400x)-24
何时获得最大利润
若设每千克西瓜的售价降低x元,每天盈利y元。
设出变量
变量关系
二次函数关系式
顶点坐标
函数的最值
解释
分析
确定
合理
解关于二次函数最值的应用题的一般思路:
求出
写出
收获与感悟
家佳源购进一批单价为20元的日用品,如果以单价30元销售,那么半个月内可以售出400件。根据销售经验,提高单价会导致销售量的减少,即销售单价每提高1元,销售量相应减少20件。如何提高售价,才能在半个月内获得最大利润?最大利润是多少?
达标检测
何时获得最大利润
解:设每件售价提高x元,半月所获利润为y元
y=(30+x-20)(400-20x)
=(10+x)(400-20x)
=-20x2+200x+4000
x=-200/-40=5
由x=5得y=(30+5-20)(400-20×5)=4500
答:当每件售价提高5元时,最大利润为4500元。
课堂寄语
二次函数是一类最优化问题的数学模型,能指导我们解决生活中的实际问题,同学们,认真学习数学吧,因为数学来源于生活,更能优化我们的生活。
布置作业,完善提升
课本65页随堂练习1,课本66页1、2
