2021-2022学年沪教新版七年级上册数学《第11章 图形的运动》单元测试卷(word版含解析)
文档属性
| 名称 | 2021-2022学年沪教新版七年级上册数学《第11章 图形的运动》单元测试卷(word版含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 323.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-27 21:04:31 | ||
图片预览


文档简介
2021-2022学年沪教新版七年级上册数学《第11章 图形的运动》单元测试卷
一.选择题
1.如图是台球桌面示意图,阴影部分表示四个入球孔,小明按图中方向击球(球可以多次反弹),则球最后落入的球袋是( )
A.1号袋 B.2号袋 C.3号袋 D.4号袋
2.如图所示是“福娃欢欢”的五幅图案,②,③,④,⑤哪一个图案可以通过平移图案①得到( )
A.② B.③ C.④ D.⑤
3.下列平移作图错误的是( )
A. B. C. D.
4.下列哪个图形是由右图平移得到的是( )
A. B. C. D.
5.下列现象中属于旋转的有( )个.
①火车行驶;②荡秋千运动;③方向盘的转动;④钟摆的运动;⑤圆规画圆.
A.1 B.2 C.3 D.4
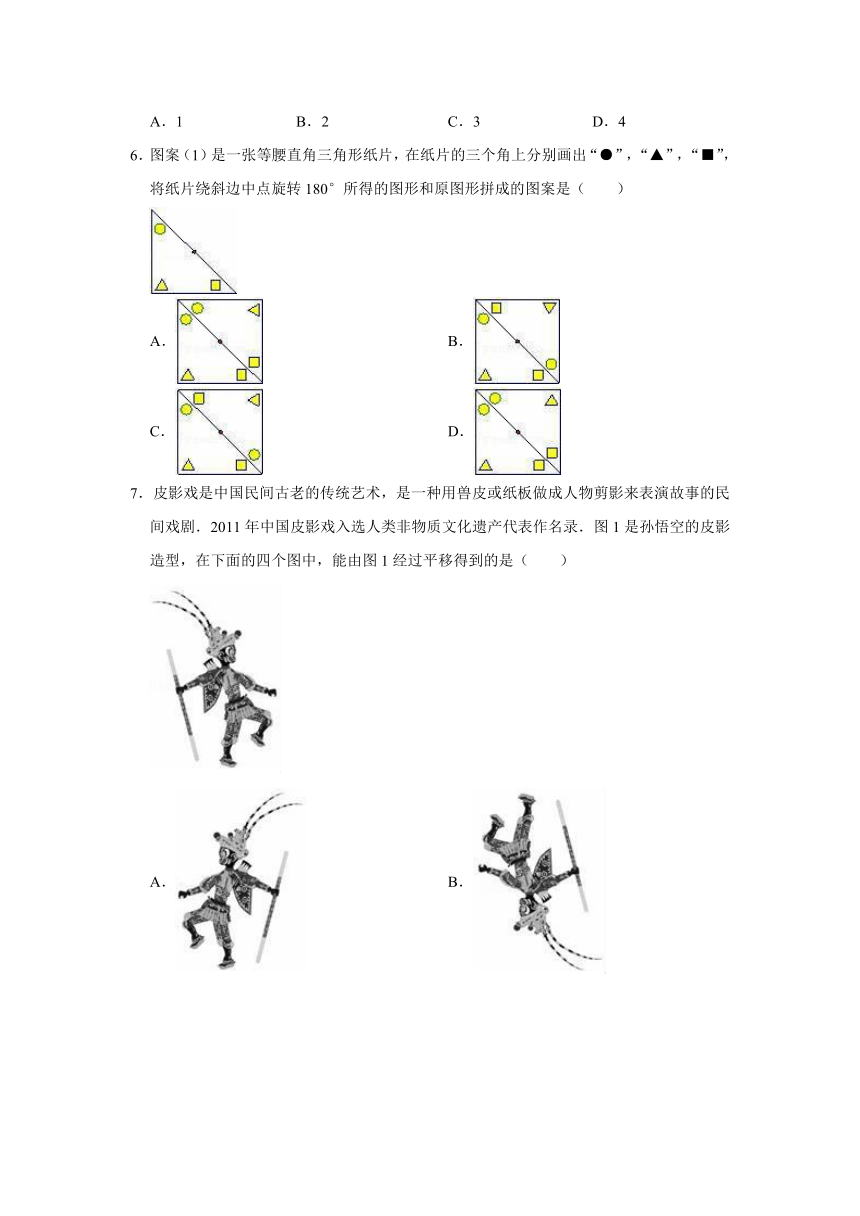
6.图案(1)是一张等腰直角三角形纸片,在纸片的三个角上分别画出“●”,“▲”,“■”,将纸片绕斜边中点旋转180°所得的图形和原图形拼成的图案是( )
A. B.
C. D.
7.皮影戏是中国民间古老的传统艺术,是一种用兽皮或纸板做成人物剪影来表演故事的民间戏剧.2011年中国皮影戏入选人类非物质文化遗产代表作名录.图1是孙悟空的皮影造型,在下面的四个图中,能由图1经过平移得到的是( )
A. B.
C. D.
8.如图是一块长方形ABCD的场地,长AB=102m,宽AD=51m,从A、B两处入口的中路宽都为1m,两小路汇合处路宽为2m,其余部分种植草坪,则草坪面积为( )
A.5050m2 B.5000m2 C.4900m2 D.4998m2
9.如图,将三角形ABE向右平移1cm得到三角形DCF,如果三角形ABE的周长是10cm,那么四边形ABFD的周长是( )
A.12cm B.16cm C.18cm D.20cm
10.国旗上的四个小五角星,通过怎样的移动可以相互得到( )
A.轴对称 B.平移 C.旋转 D.平移和旋转
二.填空题
11.如图所示,一座楼房的楼梯,高1米,水平距离是2.8米,如果要在台阶上铺一种地毯,那么至少要买这种地毯 米.
12.如图,在方格中画着两艘完全一样的小船,左边小船向右平移了 格可以来到右边小船位置.
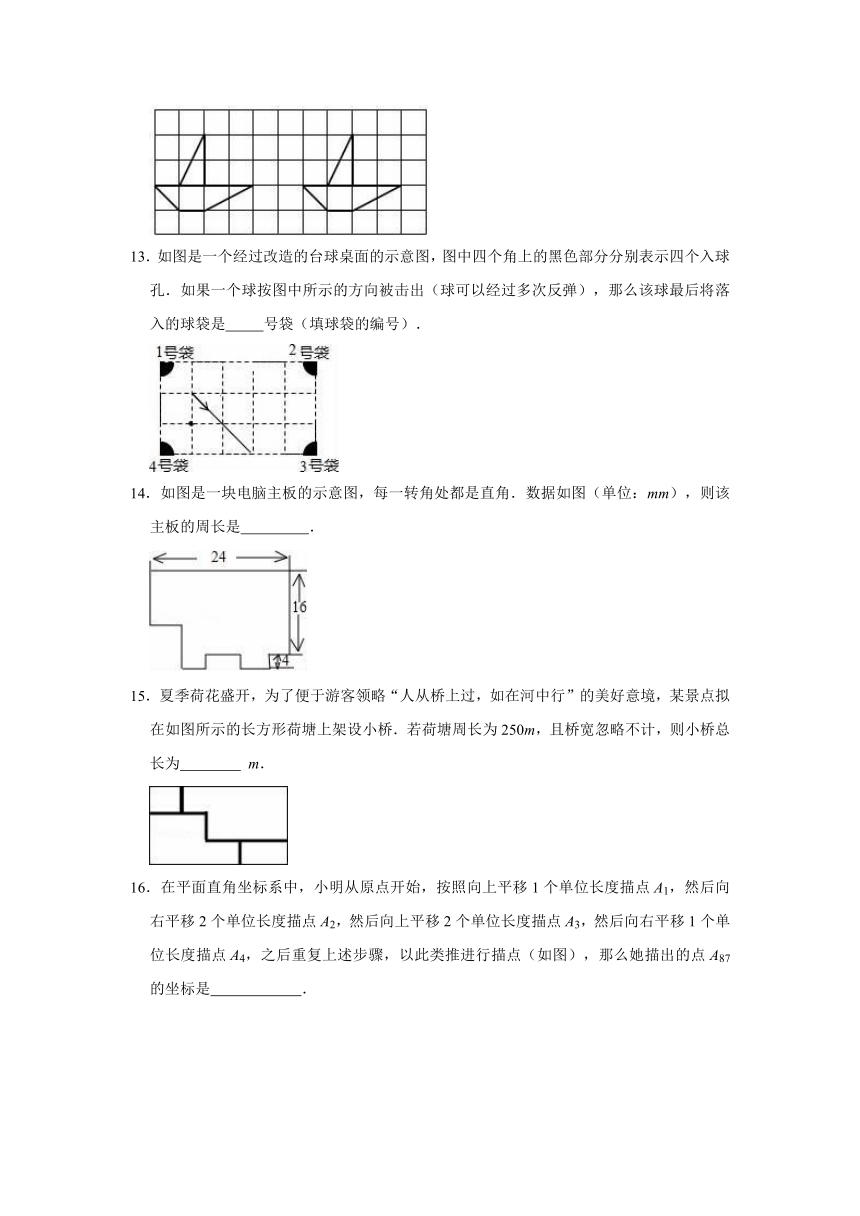
13.如图是一个经过改造的台球桌面的示意图,图中四个角上的黑色部分分别表示四个入球孔.如果一个球按图中所示的方向被击出(球可以经过多次反弹),那么该球最后将落入的球袋是 号袋(填球袋的编号).
14.如图是一块电脑主板的示意图,每一转角处都是直角.数据如图(单位:mm),则该主板的周长是 .
15.夏季荷花盛开,为了便于游客领略“人从桥上过,如在河中行”的美好意境,某景点拟在如图所示的长方形荷塘上架设小桥.若荷塘周长为250m,且桥宽忽略不计,则小桥总长为 m.
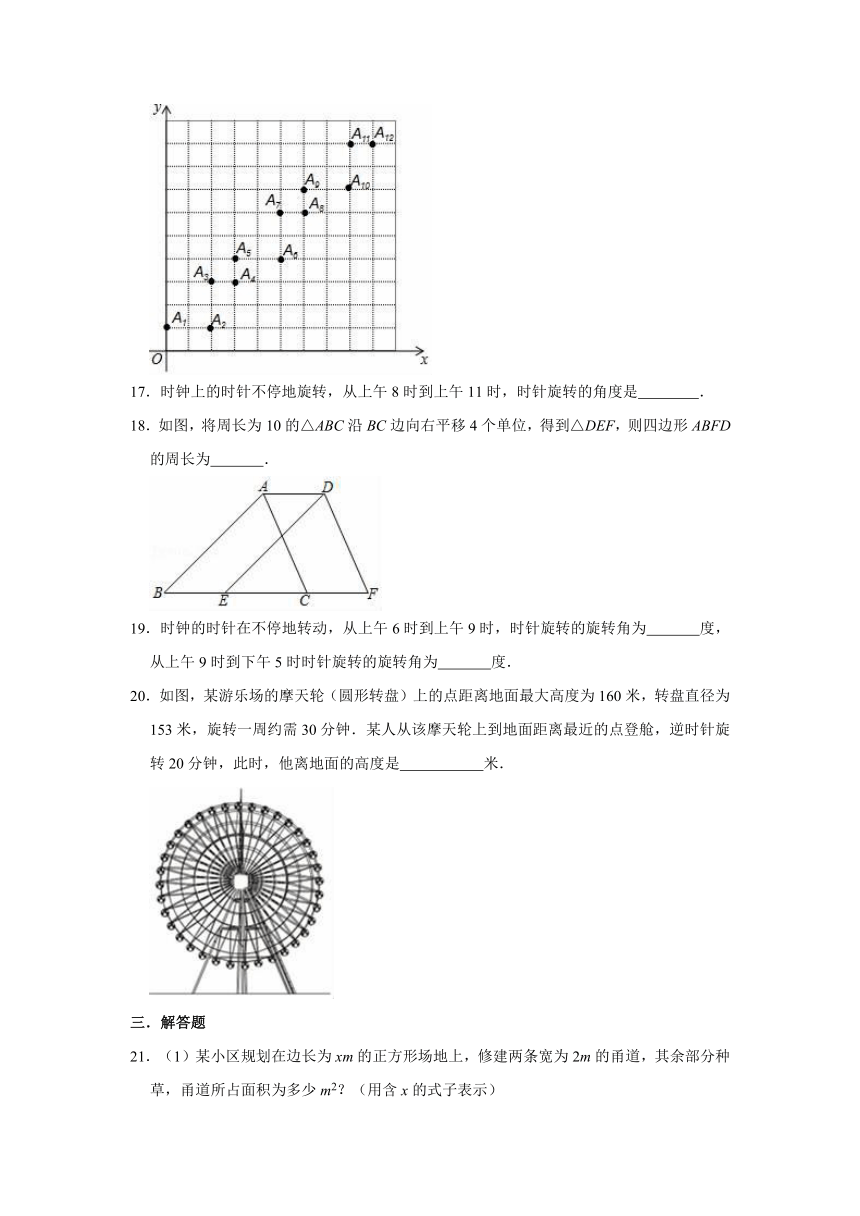
16.在平面直角坐标系中,小明从原点开始,按照向上平移1个单位长度描点A1,然后向右平移2个单位长度描点A2,然后向上平移2个单位长度描点A3,然后向右平移1个单位长度描点A4,之后重复上述步骤,以此类推进行描点(如图),那么她描出的点A87的坐标是 .
17.时钟上的时针不停地旋转,从上午8时到上午11时,时针旋转的角度是 .
18.如图,将周长为10的△ABC沿BC边向右平移4个单位,得到△DEF,则四边形ABFD的周长为 .
19.时钟的时针在不停地转动,从上午6时到上午9时,时针旋转的旋转角为 度,从上午9时到下午5时时针旋转的旋转角为 度.
20.如图,某游乐场的摩天轮(圆形转盘)上的点距离地面最大高度为160米,转盘直径为153米,旋转一周约需30分钟.某人从该摩天轮上到地面距离最近的点登舱,逆时针旋转20分钟,此时,他离地面的高度是 米.
三.解答题
21.(1)某小区规划在边长为xm的正方形场地上,修建两条宽为2m的甬道,其余部分种草,甬道所占面积为多少m2?(用含x的式子表示)
(2)该小区还有块长方形场地,将其分成了下图中的9个部分用以种植花卉,其中有⑤和⑨是正方形,其余的为长方形.
(Ⅰ)已知③④⑤⑥四个部分的周长分别为a、10、8、b,直接写出长方形场地的面积(用含a、b的式子表示);
(Ⅱ)事实上,只要知道三个部分的周长就可以求出长方形场地的面积,直接写出这三个部分的序号,要求写出两组.
22.如图,在边长为1个单位长的正方形网格图中,三角形A1B1C1是三角形ABC经过平移后得到的图形,点A,B,C均在格点上,其中A(﹣1,﹣2),C(1,﹣1),A1(3,2).
(1)在网格图中画出平面直角坐标系xOy,并写出点B的坐标;
(2)画出三角形A1B1C1,求点C1的坐标;
(3)求三角形A1B1C1的面积.
23.如图,将△ABC沿直线BC向右平移到△A1B1C1的位置,延长AC、A1B1相交于点D.
(1)求证:∠A=∠D;
(2)请写出图中3条不同类型的正确结论.
24.如图,长方形台球桌ABCD上有两个球P,Q.
(1)请画出一条路径,使得球P撞击台球桌边AB反弹后,正好撞到球Q;
(2)请画出一条路径,使得球P撞击台球桌边,经过两次反弹后,正好撞到球Q.
25.宾馆重新装修后,准备在大厅的主楼梯上铺设一种红地毯,已知这种地毯每平方米售价40元,主楼梯道宽2米,其侧面如图所示,求买地毯至少需要多少元?
26.如图,
(1)请写出在直角坐标系中的房子的A、B、C、D、E、F、G的坐标.
(2)小影想把房子向下平移3个单位长度,你能帮他办到吗?请作出相应图案,并写出平移后的7个点的坐标.
27.如图所示,一块边长为8米的正方形土地,上面修了横竖各有两条道路,宽都是2米,空白的部分种上各种花草,请利用平移的知识求出种花草的面积.
参考答案与试题解析
一.选择题
1.解:如图所示,
,
球最后落入的球袋是2号袋,
故选:B.
2.解:A、②是由旋转得到,故错误;
B、③是由轴对称得到,故错误;
C、④是由旋转得到,故错误;
D、⑤形状和大小没有变化,由平移得到,故正确.
故选:D.
3.解:A、B、D符合平移变换,C是轴对称变换.
故选:C.
4.解:A、图形属于旋转得到,故选项错误;
B、图形属于旋转得到,故选项错误;
C、图形的形状和大小没的变化,符合平移性质,故选项正确;
D、图形属于旋转得到,故选项错误.
故选:C.
5.解:根据旋转的概念,可知:
②荡秋千运动;③方向盘的转动;④钟摆的运动;⑤圆规画圆都属于旋转;
①火车行驶属于平移.
故其中属于旋转的是②③④⑤,共4个.
故选:D.
6.解:根据旋转的性质可知,
将纸片绕斜边中点旋转180°所得的图形和原图形拼成的图案是.
故选:B.
7.解:根据“平移”的定义可知,由题图经过平移得到的图形是:
.
故选:D.
8.解:由图可知:矩形ABCD中去掉小路后,草坪正好可以拼成一个新的矩形,且它的长为:(102﹣2)米,宽为(51﹣1)米.
所以草坪的面积应该是长×宽=(102﹣2)(51﹣1)=5000(米2).
故选:B.
9.解:∵△ABE的周长=AB+BE+AE=10(cm),由平移的性质可知,BC=AD=EF=1(cm),AE=DF,
∴四边形ABFD的周长=AB+BE+EF+DF+AD=10+1+1=12(cm).
故选:A.
10.解:四个小五角星通过旋转可以得到.
故选:C.
二.填空题
11.解:根据平移可得至少要买这种地毯1+2.8=3.8(米),
故答案为:3.8.
12.解:如图所示:左边小船向右平移了6格可以来到右边小船位置.
故答案为:6.
13.解:如图所示,则该球最后将落入的球袋是3号袋.
故答案为:3.
14.解:由图形可得出:
该主板的周长是:24+24+16+16+4×4=96(mm).
故答案为:96mm.
15.解:∵荷塘周长为250m,
∴小桥总长为:250÷2=125(m).
故答案为:125.
16.解:如图所示:A1(0,1),A2(2,1),A3(2,3),A4(3,3),A5(3,4),A6(5,4),A7(5,6),A8(6,6),A9(6,7),A10(8,7),A11(8,9),A12(9,9),
可得:A点每4个点位置分布规律相同,且A4(3,3),A8(2×3,2×3),A12(3×3,3×3),
∵87÷4=21…3,
∴A点经过21次循环后,又进行了3次变化,
∴A84(21×3,21×3),即(63,63),
∴A85(63,64),则A86(65,64),
故点A87的坐标是:(65,66).
故答案为:(65,66).
17.解:∵周角为360°,时针12小时转一周,
∴每小时对应的角度为:360°÷12=30°.
∵时针从上午8时到上午11时走了三个小时,
∴时针旋转的角度是:30°×3=90°.
故答案为:90°.
18.解:∵△ABC沿BC边向右平移4个单位,得到△DEF,
∴AD=BE=CF=4,AC=DF,
∵△ABC的周长为10,
∴AB+BC+AC=10,
∴四边形ABFD的周长=AB+BC+CF+DF+AD=AB+BC+AC+2AD=10+2×4=18.
故答案为18.
19.解:从上午6时到上午9时时针转过3个大格,
所以,3×30°=90°,
上午9时到下午5时时针转过8个大格,
所以,8×30°=240°.
故答案为:90;240.
20.解:设此人从点A处登舱,逆时针旋转20分钟后到达点C.
∵旋转一周约需30分钟.某人从该摩天轮上到地面距离最近的点登舱,逆时针旋转20分钟,
∴此人旋转了×20=240°,
∴∠AOC=120°.
如图,过点O作OE⊥CD于点E,则四边形BDEO是矩形,
∴DE=OB=160﹣=83.5(米).
在直角△OEC中,∵∠COE=120°﹣90°=30°,OC==76.5米,
∴CE=OC=38.25米,
∴CD=CE+DE=38.25+83.5=121.75(米).
故答案为121.75.
三.解答题
21.解:(1)S=2x+2x﹣2×2
=4x﹣4,
或者S=x2﹣(x﹣2)2=4x﹣4;
(2)(Ⅰ)设第⑨个正方形边长为x,则第③个长方形的一边为x,设另一边为y,
∵第④、⑤个正方形周长为10、8,
∴第④个长方形边长为3、2,第⑤个正方形边长为2,
则第⑥个长方形一条边为2,另一条边为x,
∴b=2x+4
∴x=﹣2
∵第③个长方形的周长为a,
∴a=2(x+y)
∴y=﹣x=﹣+2
∴长方形场地的面积为:
(3+2+﹣2)(﹣2+2+﹣+2)
=(+3)(+2)
(Ⅱ)方法同(Ⅰ)即可知:
已知③、⑤、⑦的周长
或②、④、⑨的周长
就可以求出长方形场地的面积.
22.解:(1)如图所示:点B的坐标为(2,﹣4);
(2)如图所示:A1B1C1,即为所求,点C1的坐标为(5,3);
(3)△A1B1C1的面积为:3×3﹣×1×2﹣×1×3﹣×2×3=3.5.
23.证明:(1)由平移性质,得∠B=∠A1B1C1.
又∵∠A1B1C1=∠BB1D.
∴∠B=∠BB1D,
∴AB∥A1D,
∴∠A=∠D;
(2)三条不同类型的正确结论是:
①AD∥A1C1;②BB1=CC1;③∠A=∠A1.
24.解:(1)如图,运动路径:P→M→Q,点M即为所求.
(2)如图,运动路径:P→E→F→Q,点E,点F即为所求.
25.解:如图,利用平移线段,把楼梯的横竖向上向左平移,构成一个矩形,长宽分别为6米,4米,
∴地毯的长度为6+4=10米,地毯的面积为10×2=20平方米,
∴买地毯至少需要20×40=800元.
26.解:(1)(2,3),(6,5),(10,3),(3,3),(9,3),(3,0),(9,0);
(2)如图所示
下平移3个单位长度,即所有点纵坐标减3,可得平移后坐标依次为(2,0),(6,2),(10,0),(3,0),(9,0),(3,﹣3),(9,﹣3).
27.解:由平移,可把种花草的面积看成是如图边长为4米的正方形的面积.
∴种花草的面积为:4×4=16(米2).
一.选择题
1.如图是台球桌面示意图,阴影部分表示四个入球孔,小明按图中方向击球(球可以多次反弹),则球最后落入的球袋是( )
A.1号袋 B.2号袋 C.3号袋 D.4号袋
2.如图所示是“福娃欢欢”的五幅图案,②,③,④,⑤哪一个图案可以通过平移图案①得到( )
A.② B.③ C.④ D.⑤
3.下列平移作图错误的是( )
A. B. C. D.
4.下列哪个图形是由右图平移得到的是( )
A. B. C. D.
5.下列现象中属于旋转的有( )个.
①火车行驶;②荡秋千运动;③方向盘的转动;④钟摆的运动;⑤圆规画圆.
A.1 B.2 C.3 D.4
6.图案(1)是一张等腰直角三角形纸片,在纸片的三个角上分别画出“●”,“▲”,“■”,将纸片绕斜边中点旋转180°所得的图形和原图形拼成的图案是( )
A. B.
C. D.
7.皮影戏是中国民间古老的传统艺术,是一种用兽皮或纸板做成人物剪影来表演故事的民间戏剧.2011年中国皮影戏入选人类非物质文化遗产代表作名录.图1是孙悟空的皮影造型,在下面的四个图中,能由图1经过平移得到的是( )
A. B.
C. D.
8.如图是一块长方形ABCD的场地,长AB=102m,宽AD=51m,从A、B两处入口的中路宽都为1m,两小路汇合处路宽为2m,其余部分种植草坪,则草坪面积为( )
A.5050m2 B.5000m2 C.4900m2 D.4998m2
9.如图,将三角形ABE向右平移1cm得到三角形DCF,如果三角形ABE的周长是10cm,那么四边形ABFD的周长是( )
A.12cm B.16cm C.18cm D.20cm
10.国旗上的四个小五角星,通过怎样的移动可以相互得到( )
A.轴对称 B.平移 C.旋转 D.平移和旋转
二.填空题
11.如图所示,一座楼房的楼梯,高1米,水平距离是2.8米,如果要在台阶上铺一种地毯,那么至少要买这种地毯 米.
12.如图,在方格中画着两艘完全一样的小船,左边小船向右平移了 格可以来到右边小船位置.
13.如图是一个经过改造的台球桌面的示意图,图中四个角上的黑色部分分别表示四个入球孔.如果一个球按图中所示的方向被击出(球可以经过多次反弹),那么该球最后将落入的球袋是 号袋(填球袋的编号).
14.如图是一块电脑主板的示意图,每一转角处都是直角.数据如图(单位:mm),则该主板的周长是 .
15.夏季荷花盛开,为了便于游客领略“人从桥上过,如在河中行”的美好意境,某景点拟在如图所示的长方形荷塘上架设小桥.若荷塘周长为250m,且桥宽忽略不计,则小桥总长为 m.
16.在平面直角坐标系中,小明从原点开始,按照向上平移1个单位长度描点A1,然后向右平移2个单位长度描点A2,然后向上平移2个单位长度描点A3,然后向右平移1个单位长度描点A4,之后重复上述步骤,以此类推进行描点(如图),那么她描出的点A87的坐标是 .
17.时钟上的时针不停地旋转,从上午8时到上午11时,时针旋转的角度是 .
18.如图,将周长为10的△ABC沿BC边向右平移4个单位,得到△DEF,则四边形ABFD的周长为 .
19.时钟的时针在不停地转动,从上午6时到上午9时,时针旋转的旋转角为 度,从上午9时到下午5时时针旋转的旋转角为 度.
20.如图,某游乐场的摩天轮(圆形转盘)上的点距离地面最大高度为160米,转盘直径为153米,旋转一周约需30分钟.某人从该摩天轮上到地面距离最近的点登舱,逆时针旋转20分钟,此时,他离地面的高度是 米.
三.解答题
21.(1)某小区规划在边长为xm的正方形场地上,修建两条宽为2m的甬道,其余部分种草,甬道所占面积为多少m2?(用含x的式子表示)
(2)该小区还有块长方形场地,将其分成了下图中的9个部分用以种植花卉,其中有⑤和⑨是正方形,其余的为长方形.
(Ⅰ)已知③④⑤⑥四个部分的周长分别为a、10、8、b,直接写出长方形场地的面积(用含a、b的式子表示);
(Ⅱ)事实上,只要知道三个部分的周长就可以求出长方形场地的面积,直接写出这三个部分的序号,要求写出两组.
22.如图,在边长为1个单位长的正方形网格图中,三角形A1B1C1是三角形ABC经过平移后得到的图形,点A,B,C均在格点上,其中A(﹣1,﹣2),C(1,﹣1),A1(3,2).
(1)在网格图中画出平面直角坐标系xOy,并写出点B的坐标;
(2)画出三角形A1B1C1,求点C1的坐标;
(3)求三角形A1B1C1的面积.
23.如图,将△ABC沿直线BC向右平移到△A1B1C1的位置,延长AC、A1B1相交于点D.
(1)求证:∠A=∠D;
(2)请写出图中3条不同类型的正确结论.
24.如图,长方形台球桌ABCD上有两个球P,Q.
(1)请画出一条路径,使得球P撞击台球桌边AB反弹后,正好撞到球Q;
(2)请画出一条路径,使得球P撞击台球桌边,经过两次反弹后,正好撞到球Q.
25.宾馆重新装修后,准备在大厅的主楼梯上铺设一种红地毯,已知这种地毯每平方米售价40元,主楼梯道宽2米,其侧面如图所示,求买地毯至少需要多少元?
26.如图,
(1)请写出在直角坐标系中的房子的A、B、C、D、E、F、G的坐标.
(2)小影想把房子向下平移3个单位长度,你能帮他办到吗?请作出相应图案,并写出平移后的7个点的坐标.
27.如图所示,一块边长为8米的正方形土地,上面修了横竖各有两条道路,宽都是2米,空白的部分种上各种花草,请利用平移的知识求出种花草的面积.
参考答案与试题解析
一.选择题
1.解:如图所示,
,
球最后落入的球袋是2号袋,
故选:B.
2.解:A、②是由旋转得到,故错误;
B、③是由轴对称得到,故错误;
C、④是由旋转得到,故错误;
D、⑤形状和大小没有变化,由平移得到,故正确.
故选:D.
3.解:A、B、D符合平移变换,C是轴对称变换.
故选:C.
4.解:A、图形属于旋转得到,故选项错误;
B、图形属于旋转得到,故选项错误;
C、图形的形状和大小没的变化,符合平移性质,故选项正确;
D、图形属于旋转得到,故选项错误.
故选:C.
5.解:根据旋转的概念,可知:
②荡秋千运动;③方向盘的转动;④钟摆的运动;⑤圆规画圆都属于旋转;
①火车行驶属于平移.
故其中属于旋转的是②③④⑤,共4个.
故选:D.
6.解:根据旋转的性质可知,
将纸片绕斜边中点旋转180°所得的图形和原图形拼成的图案是.
故选:B.
7.解:根据“平移”的定义可知,由题图经过平移得到的图形是:
.
故选:D.
8.解:由图可知:矩形ABCD中去掉小路后,草坪正好可以拼成一个新的矩形,且它的长为:(102﹣2)米,宽为(51﹣1)米.
所以草坪的面积应该是长×宽=(102﹣2)(51﹣1)=5000(米2).
故选:B.
9.解:∵△ABE的周长=AB+BE+AE=10(cm),由平移的性质可知,BC=AD=EF=1(cm),AE=DF,
∴四边形ABFD的周长=AB+BE+EF+DF+AD=10+1+1=12(cm).
故选:A.
10.解:四个小五角星通过旋转可以得到.
故选:C.
二.填空题
11.解:根据平移可得至少要买这种地毯1+2.8=3.8(米),
故答案为:3.8.
12.解:如图所示:左边小船向右平移了6格可以来到右边小船位置.
故答案为:6.
13.解:如图所示,则该球最后将落入的球袋是3号袋.
故答案为:3.
14.解:由图形可得出:
该主板的周长是:24+24+16+16+4×4=96(mm).
故答案为:96mm.
15.解:∵荷塘周长为250m,
∴小桥总长为:250÷2=125(m).
故答案为:125.
16.解:如图所示:A1(0,1),A2(2,1),A3(2,3),A4(3,3),A5(3,4),A6(5,4),A7(5,6),A8(6,6),A9(6,7),A10(8,7),A11(8,9),A12(9,9),
可得:A点每4个点位置分布规律相同,且A4(3,3),A8(2×3,2×3),A12(3×3,3×3),
∵87÷4=21…3,
∴A点经过21次循环后,又进行了3次变化,
∴A84(21×3,21×3),即(63,63),
∴A85(63,64),则A86(65,64),
故点A87的坐标是:(65,66).
故答案为:(65,66).
17.解:∵周角为360°,时针12小时转一周,
∴每小时对应的角度为:360°÷12=30°.
∵时针从上午8时到上午11时走了三个小时,
∴时针旋转的角度是:30°×3=90°.
故答案为:90°.
18.解:∵△ABC沿BC边向右平移4个单位,得到△DEF,
∴AD=BE=CF=4,AC=DF,
∵△ABC的周长为10,
∴AB+BC+AC=10,
∴四边形ABFD的周长=AB+BC+CF+DF+AD=AB+BC+AC+2AD=10+2×4=18.
故答案为18.
19.解:从上午6时到上午9时时针转过3个大格,
所以,3×30°=90°,
上午9时到下午5时时针转过8个大格,
所以,8×30°=240°.
故答案为:90;240.
20.解:设此人从点A处登舱,逆时针旋转20分钟后到达点C.
∵旋转一周约需30分钟.某人从该摩天轮上到地面距离最近的点登舱,逆时针旋转20分钟,
∴此人旋转了×20=240°,
∴∠AOC=120°.
如图,过点O作OE⊥CD于点E,则四边形BDEO是矩形,
∴DE=OB=160﹣=83.5(米).
在直角△OEC中,∵∠COE=120°﹣90°=30°,OC==76.5米,
∴CE=OC=38.25米,
∴CD=CE+DE=38.25+83.5=121.75(米).
故答案为121.75.
三.解答题
21.解:(1)S=2x+2x﹣2×2
=4x﹣4,
或者S=x2﹣(x﹣2)2=4x﹣4;
(2)(Ⅰ)设第⑨个正方形边长为x,则第③个长方形的一边为x,设另一边为y,
∵第④、⑤个正方形周长为10、8,
∴第④个长方形边长为3、2,第⑤个正方形边长为2,
则第⑥个长方形一条边为2,另一条边为x,
∴b=2x+4
∴x=﹣2
∵第③个长方形的周长为a,
∴a=2(x+y)
∴y=﹣x=﹣+2
∴长方形场地的面积为:
(3+2+﹣2)(﹣2+2+﹣+2)
=(+3)(+2)
(Ⅱ)方法同(Ⅰ)即可知:
已知③、⑤、⑦的周长
或②、④、⑨的周长
就可以求出长方形场地的面积.
22.解:(1)如图所示:点B的坐标为(2,﹣4);
(2)如图所示:A1B1C1,即为所求,点C1的坐标为(5,3);
(3)△A1B1C1的面积为:3×3﹣×1×2﹣×1×3﹣×2×3=3.5.
23.证明:(1)由平移性质,得∠B=∠A1B1C1.
又∵∠A1B1C1=∠BB1D.
∴∠B=∠BB1D,
∴AB∥A1D,
∴∠A=∠D;
(2)三条不同类型的正确结论是:
①AD∥A1C1;②BB1=CC1;③∠A=∠A1.
24.解:(1)如图,运动路径:P→M→Q,点M即为所求.
(2)如图,运动路径:P→E→F→Q,点E,点F即为所求.
25.解:如图,利用平移线段,把楼梯的横竖向上向左平移,构成一个矩形,长宽分别为6米,4米,
∴地毯的长度为6+4=10米,地毯的面积为10×2=20平方米,
∴买地毯至少需要20×40=800元.
26.解:(1)(2,3),(6,5),(10,3),(3,3),(9,3),(3,0),(9,0);
(2)如图所示
下平移3个单位长度,即所有点纵坐标减3,可得平移后坐标依次为(2,0),(6,2),(10,0),(3,0),(9,0),(3,﹣3),(9,﹣3).
27.解:由平移,可把种花草的面积看成是如图边长为4米的正方形的面积.
∴种花草的面积为:4×4=16(米2).
