鲁教版(五四学制)数学六年级上册1.1生活中的立体图形第二课时(共14张PPT)
文档属性
| 名称 | 鲁教版(五四学制)数学六年级上册1.1生活中的立体图形第二课时(共14张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 450.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-28 06:27:30 | ||
图片预览






文档简介
(共14张PPT)
1.1生活中的立体图形
第2课时
创设情景 明确目标
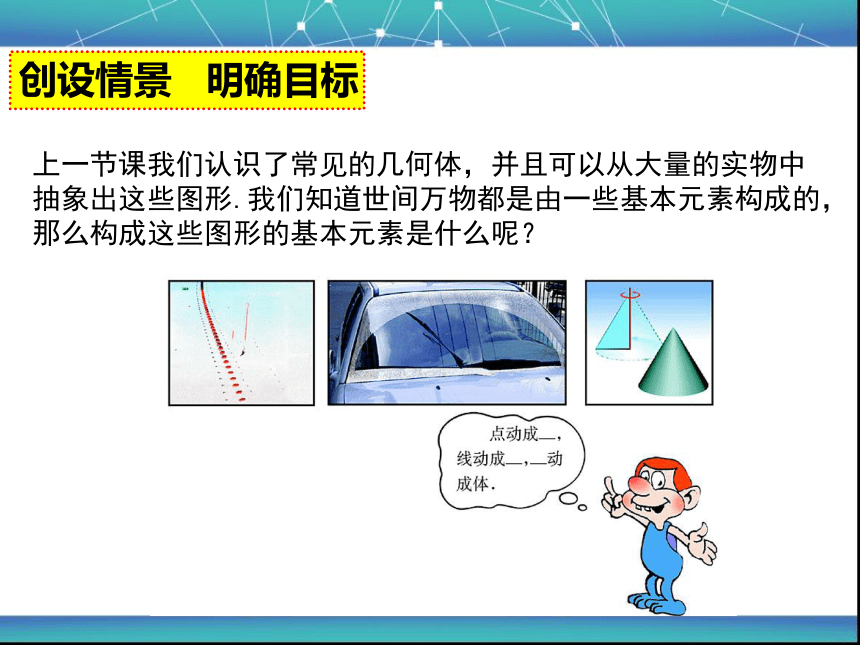
上一节课我们认识了常见的几何体,并且可以从大量的实物中抽象出这些图形.我们知道世间万物都是由一些基本元素构成的,那么构成这些图形的基本元素是什么呢?
1.通过丰富的实例,进一步认识点、线、面,初步感受点、线、面之间的关系.
2.进一步经历从现实世界中抽象出图形的过程,从构成图形的基本元素的角度认识常见几何体的某些特征.
学习目标
1.图形是由点、线、面构成的.
2.面与面相交得到线,线与线相交得到点.
3.点动成线,线动成面,面动成体.
注意线有直线和曲线之分,面有平面和曲面之分.
探究点一:点、线、面、体之间的关系
合作探究 达成目标
图中的几何体是由几个面围成的?面与面相交成几条线?它们是直的还是曲的?
探究点一:点、线、面、体之间的关系
合作探究 达成目标
点动成线
线动成面
面动成体
点线面在运动过程中与几何体的关系:
思考:旋转体是由平面几何图形如何运动形成的?
旋转体的形成:
①平面图形旋转会形成几何体;
②平面图形绕某一直线旋转一周才可以形成几何体;
③由平面图形旋转而得到的几何体有:圆柱、圆锥、球以及它们的组合体.
探究点二:认识旋转体
合作探究 达成目标
下列图形绕虚线旋转一周,能形成一个什么样的几何体?
图(1)可形成上面是圆锥,下面是圆柱的上下底面重合的几何体.
图(2)可形成一个圆柱.
图(3)可形成一个球.
图(4)可形成一个圆锥.
图(5)可形成两个底面重合的圆锥.
探究点二:认识旋转体
合作探究 达成目标
几何体的形成
(1)长方形绕其一边所在直线旋转一周得到圆柱;
(2)直角三角形绕其一条直角边所在直线旋转一周得到圆锥;
(3)半圆绕其直径所在直线旋转一周得到球体.
探究点二:认识旋转体
合作探究 达成目标
1.通过丰富的例子,知道了点、线、面是构成图形的基本元素;
2.从构成图形的基本元素的角度,进一步认识常见几何体的特征;
3. 点、线、面之间的关系:点动成线,线动成面,面动成体.
总结梳理 内化目标
达标检测 反思目标
将如图所示的直角梯形绕直线l旋转一周,得到的立体图形是( )
D
达标检测 反思目标
2.几何图形是由_____、_____、_____构成,面有_____面和_____面之分.
3.“枪挑一条线,棍扫一大片”这个现象说明:____________________.
4.长方体是由_____个面围成的,圆柱是由_____个面围成的,圆锥是由_____个面围成的.其中围成圆锥的面有_____面,也有_____面.
点
线
点动成线,线动成面
面
曲
平
六
三
二
曲
平
5.在小学里,我们曾学过圆柱的体积计算公式:
V=πR2h(R是圆柱底面半径,h为圆柱的高).
现有一个长方形,长为2cm,宽为1cm,分别
以它的两边所在的直线为轴旋转一周,得到的
几何体的体积分别是多少 它们之间有何关系
达标检测 反思目标
解:(1)当以长方形的宽所在的直线为轴旋转时,如图 ①,得到的圆柱的底面半径为2cm,高为1cm.
所以其体积V1=π×22×1=4π(cm3).
(2)当以长方形的长所在的直线为轴旋转时,如图②,得到的圆柱的底面半径为1cm,高为2cm,
所以其体积V2=π×12×2=2π(cm3).
因此,得到的两个几何体的体积之间的关系为V1=2V2.
达标检测 反思目标
1.1生活中的立体图形
第2课时
创设情景 明确目标
上一节课我们认识了常见的几何体,并且可以从大量的实物中抽象出这些图形.我们知道世间万物都是由一些基本元素构成的,那么构成这些图形的基本元素是什么呢?
1.通过丰富的实例,进一步认识点、线、面,初步感受点、线、面之间的关系.
2.进一步经历从现实世界中抽象出图形的过程,从构成图形的基本元素的角度认识常见几何体的某些特征.
学习目标
1.图形是由点、线、面构成的.
2.面与面相交得到线,线与线相交得到点.
3.点动成线,线动成面,面动成体.
注意线有直线和曲线之分,面有平面和曲面之分.
探究点一:点、线、面、体之间的关系
合作探究 达成目标
图中的几何体是由几个面围成的?面与面相交成几条线?它们是直的还是曲的?
探究点一:点、线、面、体之间的关系
合作探究 达成目标
点动成线
线动成面
面动成体
点线面在运动过程中与几何体的关系:
思考:旋转体是由平面几何图形如何运动形成的?
旋转体的形成:
①平面图形旋转会形成几何体;
②平面图形绕某一直线旋转一周才可以形成几何体;
③由平面图形旋转而得到的几何体有:圆柱、圆锥、球以及它们的组合体.
探究点二:认识旋转体
合作探究 达成目标
下列图形绕虚线旋转一周,能形成一个什么样的几何体?
图(1)可形成上面是圆锥,下面是圆柱的上下底面重合的几何体.
图(2)可形成一个圆柱.
图(3)可形成一个球.
图(4)可形成一个圆锥.
图(5)可形成两个底面重合的圆锥.
探究点二:认识旋转体
合作探究 达成目标
几何体的形成
(1)长方形绕其一边所在直线旋转一周得到圆柱;
(2)直角三角形绕其一条直角边所在直线旋转一周得到圆锥;
(3)半圆绕其直径所在直线旋转一周得到球体.
探究点二:认识旋转体
合作探究 达成目标
1.通过丰富的例子,知道了点、线、面是构成图形的基本元素;
2.从构成图形的基本元素的角度,进一步认识常见几何体的特征;
3. 点、线、面之间的关系:点动成线,线动成面,面动成体.
总结梳理 内化目标
达标检测 反思目标
将如图所示的直角梯形绕直线l旋转一周,得到的立体图形是( )
D
达标检测 反思目标
2.几何图形是由_____、_____、_____构成,面有_____面和_____面之分.
3.“枪挑一条线,棍扫一大片”这个现象说明:____________________.
4.长方体是由_____个面围成的,圆柱是由_____个面围成的,圆锥是由_____个面围成的.其中围成圆锥的面有_____面,也有_____面.
点
线
点动成线,线动成面
面
曲
平
六
三
二
曲
平
5.在小学里,我们曾学过圆柱的体积计算公式:
V=πR2h(R是圆柱底面半径,h为圆柱的高).
现有一个长方形,长为2cm,宽为1cm,分别
以它的两边所在的直线为轴旋转一周,得到的
几何体的体积分别是多少 它们之间有何关系
达标检测 反思目标
解:(1)当以长方形的宽所在的直线为轴旋转时,如图 ①,得到的圆柱的底面半径为2cm,高为1cm.
所以其体积V1=π×22×1=4π(cm3).
(2)当以长方形的长所在的直线为轴旋转时,如图②,得到的圆柱的底面半径为1cm,高为2cm,
所以其体积V2=π×12×2=2π(cm3).
因此,得到的两个几何体的体积之间的关系为V1=2V2.
达标检测 反思目标
