苏科版九年级数学上册 2.1 圆(课件)(共37张PPT)
文档属性
| 名称 | 苏科版九年级数学上册 2.1 圆(课件)(共37张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-28 00:00:00 | ||
图片预览







文档简介
(共37张PPT)
2.1 圆
红日、满月、车轮、硬币……圆的形象处处可见.
平面图形中,圆象征着完美、和谐和对称.
圆的世界
2.1 圆(第1课时)
苏教版九上
1.用圆规画一个圆?试着说说你画圆的步骤。
【活动一】
思考:
通过这些操作,你能说说圆是怎样形成的吗?
2.给你一段两端打结的棉线和一支粉笔,你和同桌能
用它们在地上画出圆吗?你是怎么做的?
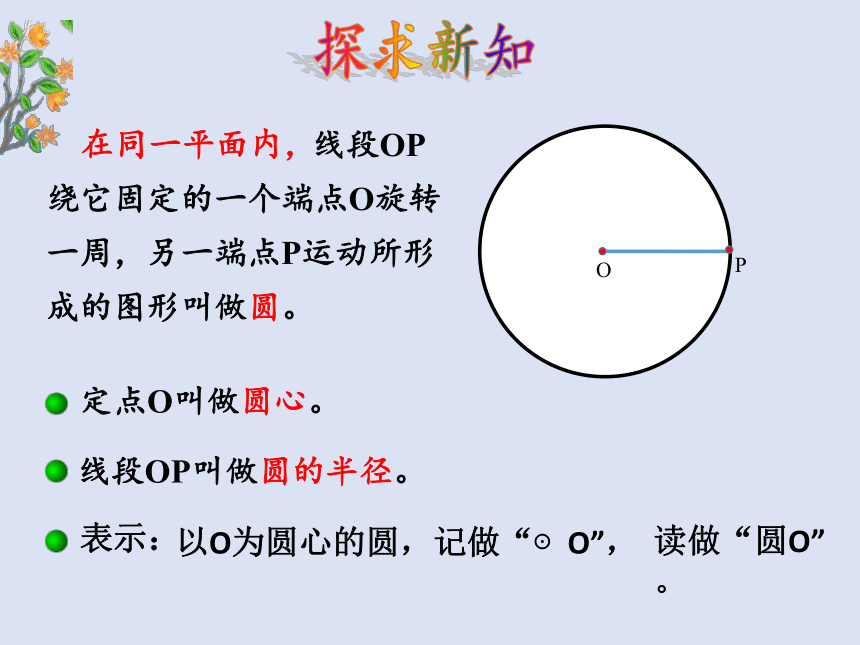
线段OP绕它固定的一个端点O旋转一周,另一端点P运动所形成的图形叫做圆。
定点O叫做圆心。
线段OP叫做圆的半径。
表示:
以O为圆心的圆,记做“⊙O”,
读做“圆O”。
在同一平面内,
探求新知
O
P
●
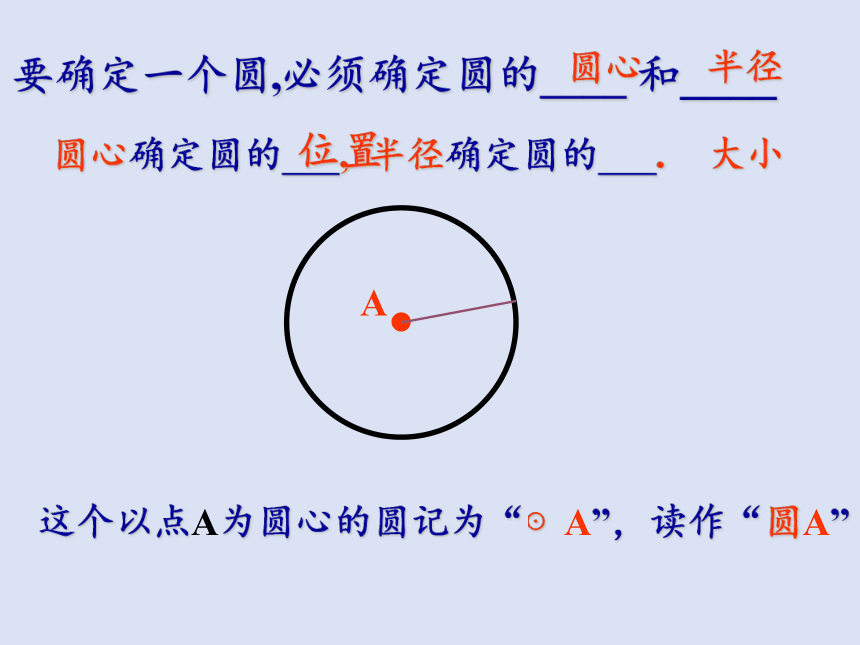
要确定一个圆,必须确定圆的____ 和____
圆心
半径
圆心确定圆的 , 半径确定圆的 .
A
这个以点A为圆心的圆记为“⊙A”,读作“圆A”
位置
大小
关于定义的几点说明:
1.要注意“在平面内”的条件
2.“圆”是一条封闭的曲线,不是“圆面’
3.确定圆的要素是 ,两者缺一不可
圆心和半径
套圈游戏
生活·活动
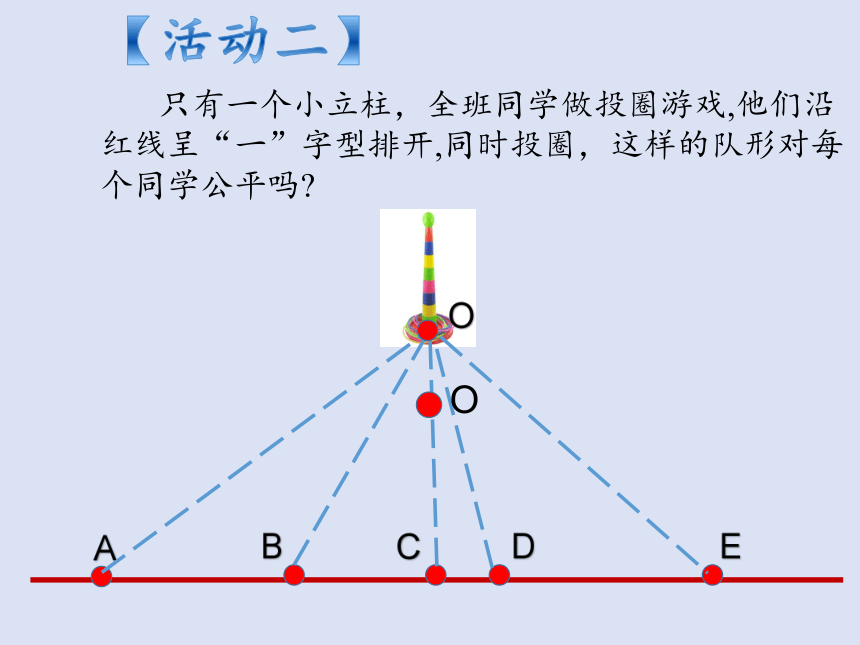
【活动二】
只有一个小立柱,全班同学做投圈游戏,他们沿红线呈“一”字型排开,同时投圈,这样的队形对每个同学公平吗
A
B
C
D
E
O
O
O
A
B
C
E
D
点在圆上
圆上各点到圆心的距离都等于半径
到圆心的距离等于半径的点在圆上
反过来,
【活动二】
思考:
为什么围成圆形游戏就公平?
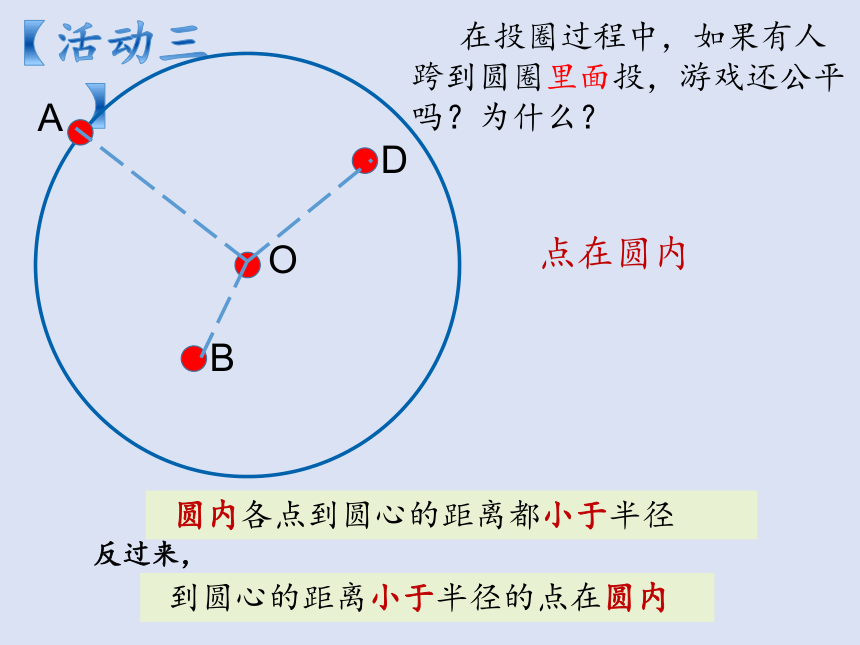
【活动三】
O
A
D
在投圈过程中,如果有人跨到圆圈里面投,游戏还公平吗?为什么?
B
点在圆内
圆内各点到圆心的距离都小于半径
到圆心的距离小于半径的点在圆内
反过来,
【活动三】
O
A
C
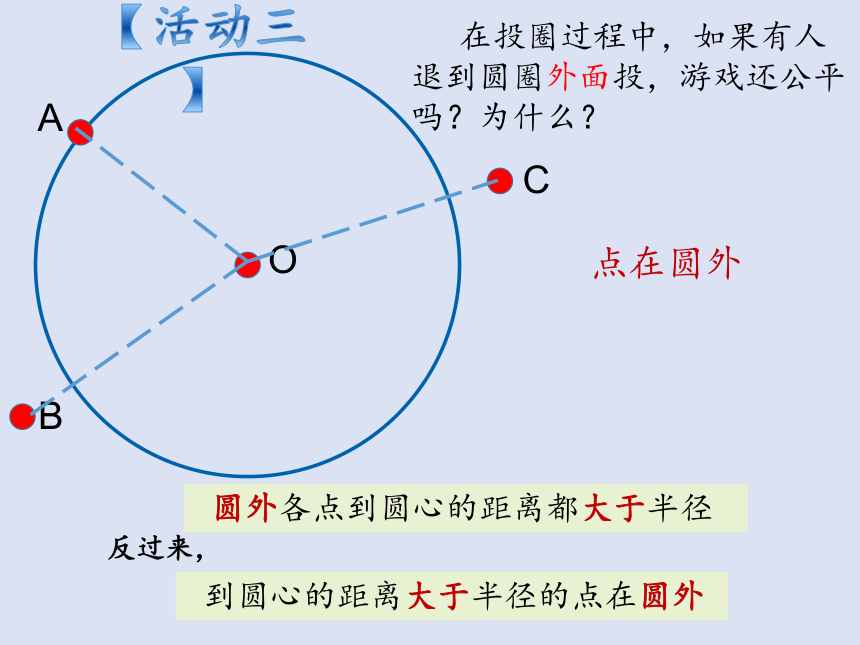
在投圈过程中,如果有人退到圆圈外面投,游戏还公平吗?为什么?
B
点在圆外
圆外各点到圆心的距离都大于半径
到圆心的距离大于半径的点在圆外
反过来,
A
B
C
O
在一个平面内,点与圆有哪几种位置关系呢?
点A在圆内
点B在圆上
点C在圆外
点与圆的位置关系
点在圆内
点在圆上
点在圆外
点到圆心的距离都小于半径
点到圆心的距离与圆的半径的数量关系
点到圆心的距离都等于半径
点到圆心的距离都大于半径
设⊙O 的半径为r,点P到圆心O的距离OP = d,
点P在⊙O内
点P在⊙O上
点P在⊙O外
点与圆的位置关系
d<r
d=r
d>r
r
p
d
p
r
d
P
r
d
圆是到定点(圆心)距离等于定长(半径)的点的集合.
r
圆的集合定义
圆是到定点距离等于定长的点的集合.
车轮为什么做成圆形
圆的集合定义
圆外的点
圆内的点
圆上的点
思考:
平面上的一个圆把平面上的点分成哪几部分?
圆是 点的集合.
平面内到定点(圆心)的距离等于定长(半径)的
圆的内部是 点的集合.
圆的外部是 点的集合.
平面内到圆心的距离小于半径的
平面内到圆心的距离大于半径的
数学·思考
想一想:
总结:
*圆上各点到圆心(定点)的距离都等于半径(定长);
到圆心距离等于半径的点都在圆上.
也就是说:圆是到定点距离等于定长的点的集合.
*圆内各点到圆心的距离都小于半径;
到圆心距离小于半径的点都在圆内.
也就是说:圆的内部可以看作是到圆心距离小于半径
的点的集合.
*圆外各点到圆心的距离都大于半径;
到圆心距离大于半径的点都在圆外.
也就是说:圆的外部可以看作是到圆心距离大于半径
的点的集合.
例1:已知⊙O的半径为4cm,如果点P 到圆心O的距离为4.5cm,那么点P与⊙O有怎样的位置关系?
如果点P 到圆心O的距离为4cm、3cm呢?
如何判断点与圆的位置关系?
只需要比较点到圆心的距离d与半径r的大小关系.
解:
设⊙O的半径为rcm,点P到圆心O的距离为dcm.
由题意得,r=4cm.
当d=4.5cm时, ∵ d>r,∴点P在⊙O外.
当d=4cm时, ∵ d=r,∴点P在⊙O上.
当d=3cm时, ∵ d<r,∴点P在⊙O内.
知识运用
例2:如图,已知点A,请作出到点A的距离等于2cm的点的集合.
(1)这个圆的外部是满足什么条件的点的集合?
(2)请用阴影表示到点A的距离小于或等于2cm的点的集合.
A
知识运用
如图,已知点A、B,且AB=4cm.
(1)画出下列图形:
到点A的距离等于2cm的点的集合;
到点B的距离等于3cm的点的集合.
(2)在所画图中,到点A的距离等于2cm,且到点B的距离等于
3cm的点有几个?请在图中将它们表示出来.
(3)在所画图中,到点A的距离小于或等于2cm,且到点B的距
离大于或等于3cm的点的集合是怎样的图形?
P
Q
B
拓展运用
A
2cm
3cm
通过今天的学习,你能谈谈你对圆有什么新的认识吗?
小结与思考
已知:如图,BD、CE是△ABC的高,M为BC的中点.
试说明点 B、C、D、E在以点M为圆心的同一圆上.
解题的依据:
要说明几点在同一个圆上,即说明这几个点到定点(圆心)的距离等于定长(半径).
到定点的距离等于定长的点在同一个圆上.
拓展运用
∴点B、C、D、E在以点M为圆心,
为半径的圆上.
解:
连接MD、ME.
∵BD、CE是△ABC的高,
∴∠BEC=∠BDC=90°.
在Rt△BEC中,M为BC的中点,
同理,
∴MB=ME=MD=MC,
又∵
已知:如图,BD、CE是△ABC的高,M为BC的中点.
试说明点 B、C、D、E在以点M 为圆心的同一圆上.
1.已知⊙O的半径为5。
(1)若PO=5.5,则点P在 ;
(2)若PO=4,则点P在 ;
(3)若PO= ,则点P在圆上。
圆外
圆内
5
练一练:
(4)若点P在圆内时OP ;
若点P不在圆外时OP 。
<5
≤5
o
练一练
2.到定点o的距离为2cm的点的集合
是以 为圆心, 为半径的圆。
o
2cm
3.如图已知矩形ABCD的边AB=3cm,AD=4cm
A
D
C
B
(1)以点A为圆心,3cm为半径作圆A,
则点B、C、D与圆A的位置关系如何?
(B在圆上,D在圆外,C在圆外)
(2)以点A为圆心,4cm为半径作圆A,
则点B、C、D与圆A的位置关系如何?
(B在圆内,D在圆上,C在圆外)
(3)以点A为圆心,5cm为半径作圆A,
则点B、C、D与圆A的位置关系如何?
(B在圆内,D在圆内,C在圆上)
练一练
1.⊙O的半径10cm,A、B、C三点到圆心的距离分别为8cm、10cm、12cm,则点A、B、C与⊙O的位置关系是:点A在 ;点B在 ;点C在 。
2.⊙O的半径6cm,当OP=6时,点A在 ;
当OP 时点P在圆内;当OP 时,点P不在圆外。
3.正方形ABCD的边长为2cm,以A为圆心2cm为半径作⊙A,则点B在⊙A ;点C在⊙A ;点D在⊙A 。
圆内
圆上
圆外
圆上
<6
≤6
上
外
上
4.已知AB为⊙O的直径P为⊙O 上任意一点,则点关于AB的对称点P′与⊙O的位置为( )
(A)在⊙O内 (B)在⊙O 外 (C)在⊙O 上 (D)不能确定
c
5.如图,直角△ABC中,∠C=90°,以AB为直径画⊙O.判断点C与⊙O的位置关系并说明理由。
A
C
B
O
拓展:
任意一个矩形的四个顶点是否在同一个圆上?如果在,请描述这个圆?
A
B
D
C
能力提高
2005年9月11日,第十五号台风“卡努”登陆浙江,A市接到台风警报时,台风中心位于A市正南方向125km的B处,正以15km/h的速度沿BC方向移动。
已知A市到BC的距离AD=35km,如果在距离台风中心40km(包括40km)的区域内都将受到台风影响
试问A市受到台风影响的时间是多长?
问题1:请用点与圆的位置关系
描述A市何时受到台风影响?
问题2:请用点到圆心的距离和圆的半径的大小
关系表示出A市何时受台风影响?
谢 谢
2.1 圆
红日、满月、车轮、硬币……圆的形象处处可见.
平面图形中,圆象征着完美、和谐和对称.
圆的世界
2.1 圆(第1课时)
苏教版九上
1.用圆规画一个圆?试着说说你画圆的步骤。
【活动一】
思考:
通过这些操作,你能说说圆是怎样形成的吗?
2.给你一段两端打结的棉线和一支粉笔,你和同桌能
用它们在地上画出圆吗?你是怎么做的?
线段OP绕它固定的一个端点O旋转一周,另一端点P运动所形成的图形叫做圆。
定点O叫做圆心。
线段OP叫做圆的半径。
表示:
以O为圆心的圆,记做“⊙O”,
读做“圆O”。
在同一平面内,
探求新知
O
P
●
要确定一个圆,必须确定圆的____ 和____
圆心
半径
圆心确定圆的 , 半径确定圆的 .
A
这个以点A为圆心的圆记为“⊙A”,读作“圆A”
位置
大小
关于定义的几点说明:
1.要注意“在平面内”的条件
2.“圆”是一条封闭的曲线,不是“圆面’
3.确定圆的要素是 ,两者缺一不可
圆心和半径
套圈游戏
生活·活动
【活动二】
只有一个小立柱,全班同学做投圈游戏,他们沿红线呈“一”字型排开,同时投圈,这样的队形对每个同学公平吗
A
B
C
D
E
O
O
O
A
B
C
E
D
点在圆上
圆上各点到圆心的距离都等于半径
到圆心的距离等于半径的点在圆上
反过来,
【活动二】
思考:
为什么围成圆形游戏就公平?
【活动三】
O
A
D
在投圈过程中,如果有人跨到圆圈里面投,游戏还公平吗?为什么?
B
点在圆内
圆内各点到圆心的距离都小于半径
到圆心的距离小于半径的点在圆内
反过来,
【活动三】
O
A
C
在投圈过程中,如果有人退到圆圈外面投,游戏还公平吗?为什么?
B
点在圆外
圆外各点到圆心的距离都大于半径
到圆心的距离大于半径的点在圆外
反过来,
A
B
C
O
在一个平面内,点与圆有哪几种位置关系呢?
点A在圆内
点B在圆上
点C在圆外
点与圆的位置关系
点在圆内
点在圆上
点在圆外
点到圆心的距离都小于半径
点到圆心的距离与圆的半径的数量关系
点到圆心的距离都等于半径
点到圆心的距离都大于半径
设⊙O 的半径为r,点P到圆心O的距离OP = d,
点P在⊙O内
点P在⊙O上
点P在⊙O外
点与圆的位置关系
d<r
d=r
d>r
r
p
d
p
r
d
P
r
d
圆是到定点(圆心)距离等于定长(半径)的点的集合.
r
圆的集合定义
圆是到定点距离等于定长的点的集合.
车轮为什么做成圆形
圆的集合定义
圆外的点
圆内的点
圆上的点
思考:
平面上的一个圆把平面上的点分成哪几部分?
圆是 点的集合.
平面内到定点(圆心)的距离等于定长(半径)的
圆的内部是 点的集合.
圆的外部是 点的集合.
平面内到圆心的距离小于半径的
平面内到圆心的距离大于半径的
数学·思考
想一想:
总结:
*圆上各点到圆心(定点)的距离都等于半径(定长);
到圆心距离等于半径的点都在圆上.
也就是说:圆是到定点距离等于定长的点的集合.
*圆内各点到圆心的距离都小于半径;
到圆心距离小于半径的点都在圆内.
也就是说:圆的内部可以看作是到圆心距离小于半径
的点的集合.
*圆外各点到圆心的距离都大于半径;
到圆心距离大于半径的点都在圆外.
也就是说:圆的外部可以看作是到圆心距离大于半径
的点的集合.
例1:已知⊙O的半径为4cm,如果点P 到圆心O的距离为4.5cm,那么点P与⊙O有怎样的位置关系?
如果点P 到圆心O的距离为4cm、3cm呢?
如何判断点与圆的位置关系?
只需要比较点到圆心的距离d与半径r的大小关系.
解:
设⊙O的半径为rcm,点P到圆心O的距离为dcm.
由题意得,r=4cm.
当d=4.5cm时, ∵ d>r,∴点P在⊙O外.
当d=4cm时, ∵ d=r,∴点P在⊙O上.
当d=3cm时, ∵ d<r,∴点P在⊙O内.
知识运用
例2:如图,已知点A,请作出到点A的距离等于2cm的点的集合.
(1)这个圆的外部是满足什么条件的点的集合?
(2)请用阴影表示到点A的距离小于或等于2cm的点的集合.
A
知识运用
如图,已知点A、B,且AB=4cm.
(1)画出下列图形:
到点A的距离等于2cm的点的集合;
到点B的距离等于3cm的点的集合.
(2)在所画图中,到点A的距离等于2cm,且到点B的距离等于
3cm的点有几个?请在图中将它们表示出来.
(3)在所画图中,到点A的距离小于或等于2cm,且到点B的距
离大于或等于3cm的点的集合是怎样的图形?
P
Q
B
拓展运用
A
2cm
3cm
通过今天的学习,你能谈谈你对圆有什么新的认识吗?
小结与思考
已知:如图,BD、CE是△ABC的高,M为BC的中点.
试说明点 B、C、D、E在以点M为圆心的同一圆上.
解题的依据:
要说明几点在同一个圆上,即说明这几个点到定点(圆心)的距离等于定长(半径).
到定点的距离等于定长的点在同一个圆上.
拓展运用
∴点B、C、D、E在以点M为圆心,
为半径的圆上.
解:
连接MD、ME.
∵BD、CE是△ABC的高,
∴∠BEC=∠BDC=90°.
在Rt△BEC中,M为BC的中点,
同理,
∴MB=ME=MD=MC,
又∵
已知:如图,BD、CE是△ABC的高,M为BC的中点.
试说明点 B、C、D、E在以点M 为圆心的同一圆上.
1.已知⊙O的半径为5。
(1)若PO=5.5,则点P在 ;
(2)若PO=4,则点P在 ;
(3)若PO= ,则点P在圆上。
圆外
圆内
5
练一练:
(4)若点P在圆内时OP ;
若点P不在圆外时OP 。
<5
≤5
o
练一练
2.到定点o的距离为2cm的点的集合
是以 为圆心, 为半径的圆。
o
2cm
3.如图已知矩形ABCD的边AB=3cm,AD=4cm
A
D
C
B
(1)以点A为圆心,3cm为半径作圆A,
则点B、C、D与圆A的位置关系如何?
(B在圆上,D在圆外,C在圆外)
(2)以点A为圆心,4cm为半径作圆A,
则点B、C、D与圆A的位置关系如何?
(B在圆内,D在圆上,C在圆外)
(3)以点A为圆心,5cm为半径作圆A,
则点B、C、D与圆A的位置关系如何?
(B在圆内,D在圆内,C在圆上)
练一练
1.⊙O的半径10cm,A、B、C三点到圆心的距离分别为8cm、10cm、12cm,则点A、B、C与⊙O的位置关系是:点A在 ;点B在 ;点C在 。
2.⊙O的半径6cm,当OP=6时,点A在 ;
当OP 时点P在圆内;当OP 时,点P不在圆外。
3.正方形ABCD的边长为2cm,以A为圆心2cm为半径作⊙A,则点B在⊙A ;点C在⊙A ;点D在⊙A 。
圆内
圆上
圆外
圆上
<6
≤6
上
外
上
4.已知AB为⊙O的直径P为⊙O 上任意一点,则点关于AB的对称点P′与⊙O的位置为( )
(A)在⊙O内 (B)在⊙O 外 (C)在⊙O 上 (D)不能确定
c
5.如图,直角△ABC中,∠C=90°,以AB为直径画⊙O.判断点C与⊙O的位置关系并说明理由。
A
C
B
O
拓展:
任意一个矩形的四个顶点是否在同一个圆上?如果在,请描述这个圆?
A
B
D
C
能力提高
2005年9月11日,第十五号台风“卡努”登陆浙江,A市接到台风警报时,台风中心位于A市正南方向125km的B处,正以15km/h的速度沿BC方向移动。
已知A市到BC的距离AD=35km,如果在距离台风中心40km(包括40km)的区域内都将受到台风影响
试问A市受到台风影响的时间是多长?
问题1:请用点与圆的位置关系
描述A市何时受到台风影响?
问题2:请用点到圆心的距离和圆的半径的大小
关系表示出A市何时受台风影响?
谢 谢
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
