1.1菱形的性质与判定 复习训练 2021-2022学年北师大版九年级数学上册(Word版含答案)
文档属性
| 名称 | 1.1菱形的性质与判定 复习训练 2021-2022学年北师大版九年级数学上册(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 337.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-27 20:20:40 | ||
图片预览


文档简介
2021-2022学年北师大版九年级数学上册《1.1菱形的性质与判定》期中复习训练(附答案)
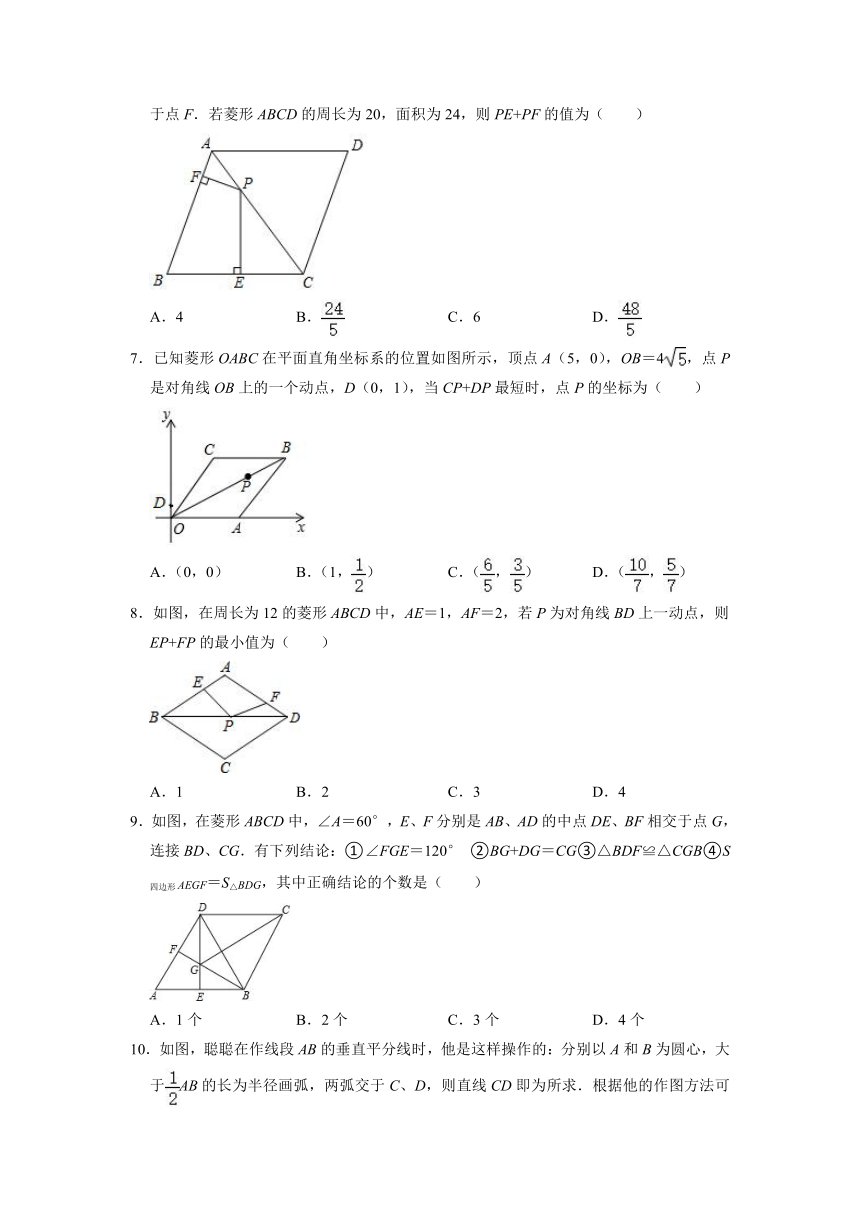
1.下列选项中能使 ABCD成为菱形的是( )
A.AB=CD B.AB=BC C.∠BAD=90° D.AC=BD
2.如图,在直角坐标系中,菱形ABCD的顶点A,B,C在坐标轴上,若点B的坐标为(﹣1,0),∠BCD=120°,则点D的坐标为( )
A.(2,2) B.(,2) C.(3,) D.(2,)
3.如图,在菱形ABCD中,对角线AC=8,BD=10,则△AOD的面积为( )
A.9 B.10 C.11 D.12
4.如图,在菱形ABCD中,∠A=60°,点E,F分别在边AB,BC上,AE=BF=2,△DEF的周长为3,则AD的长为( )
A. B.2 C.+1 D.2﹣1
5.如图,点E,F在菱形ABCD的对角线AC上,∠ADC=120°,∠BEC=∠CBF=50°,ED与BF的延长线交于点M.则对于以下结论:①∠BME=30°;②△ADE≌△ABE;③EM=BC;④AE+BM=EM.其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
6.如图,在菱形ABCD中,P是对角线AC上一动点,过点P作PE⊥BC于点E.PF⊥AB于点F.若菱形ABCD的周长为20,面积为24,则PE+PF的值为( )
A.4 B. C.6 D.
7.已知菱形OABC在平面直角坐标系的位置如图所示,顶点A(5,0),OB=4,点P是对角线OB上的一个动点,D(0,1),当CP+DP最短时,点P的坐标为( )
A.(0,0) B.(1,) C.(,) D.(,)
8.如图,在周长为12的菱形ABCD中,AE=1,AF=2,若P为对角线BD上一动点,则EP+FP的最小值为( )
A.1 B.2 C.3 D.4
9.如图,在菱形ABCD中,∠A=60°,E、F分别是AB、AD的中点DE、BF相交于点G,连接BD、CG.有下列结论:①∠FGE=120° ②BG+DG=CG③△BDF≌△CGB④S四边形AEGF=S△BDG,其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
10.如图,聪聪在作线段AB的垂直平分线时,他是这样操作的:分别以A和B为圆心,大于AB的长为半径画弧,两弧交于C、D,则直线CD即为所求.根据他的作图方法可知四边形ADBC一定是( )
A.菱形 B.矩形 C.正方形 D.等腰梯形
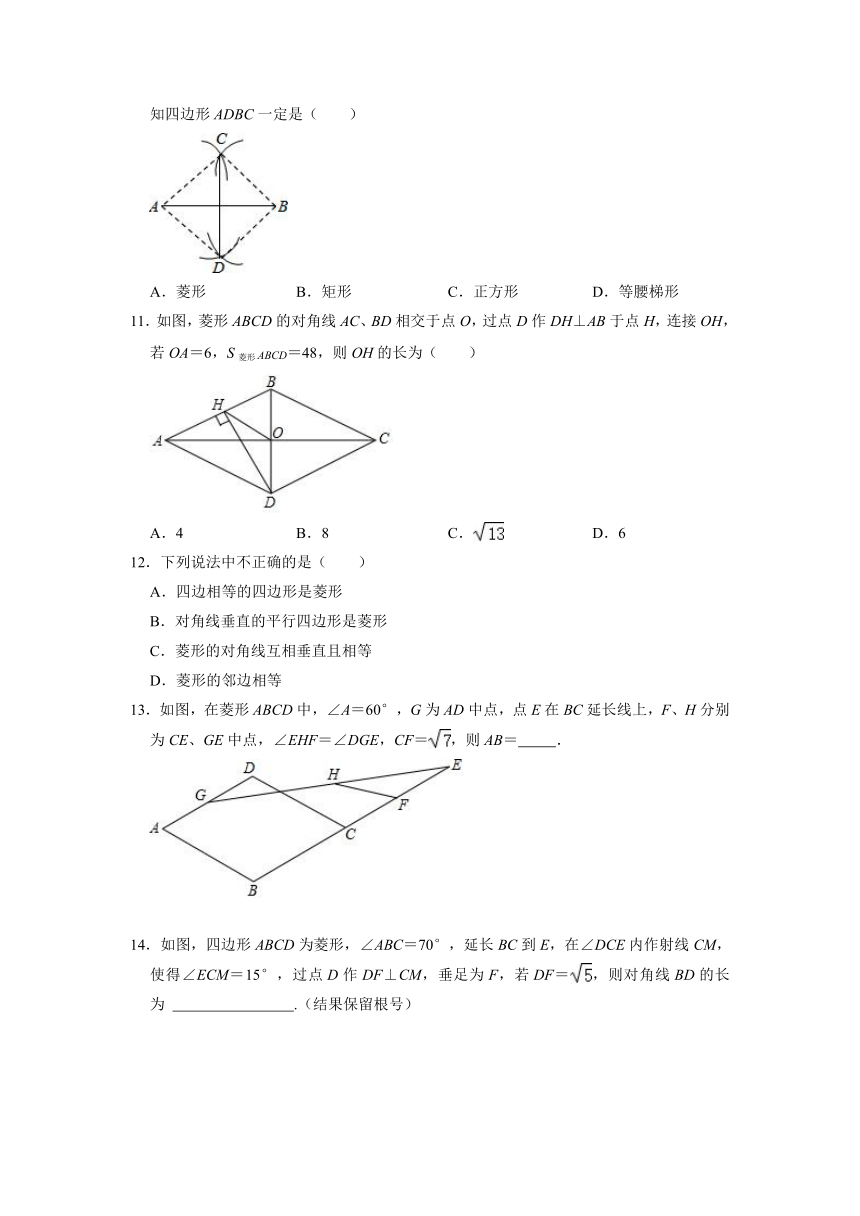
11.如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DH⊥AB于点H,连接OH,若OA=6,S菱形ABCD=48,则OH的长为( )
A.4 B.8 C. D.6
12.下列说法中不正确的是( )
A.四边相等的四边形是菱形
B.对角线垂直的平行四边形是菱形
C.菱形的对角线互相垂直且相等
D.菱形的邻边相等
13.如图,在菱形ABCD中,∠A=60°,G为AD中点,点E在BC延长线上,F、H分别为CE、GE中点,∠EHF=∠DGE,CF=,则AB= .
14.如图,四边形ABCD为菱形,∠ABC=70°,延长BC到E,在∠DCE内作射线CM,使得∠ECM=15°,过点D作DF⊥CM,垂足为F,若DF=,则对角线BD的长为 .(结果保留根号)
15.如图,将两张对边平行且等宽的纸条交叉叠放在一起,则重合部分构成的四边形ABCD 菱形(填“是”或“不是”).
16.已知:如图,在 ABCD中,点E、F分别在AD、BC上,且BE平分∠ABC,EF∥AB.求证:四边形ABFE是菱形.
17.如图,在 ABCD中,G为BC边上一点,DG=DC,延长DG交AB的延长线于点E,过点A作AF∥ED交CD的延长线于点F.求证:四边形AEDF是菱形.
18.如图,在菱形ABCD中,E,F是对角线AC上的两点,且AE=CF.
(1)求证:△ABE≌△CDF;
(2)求证:四边形BEDF是菱形.
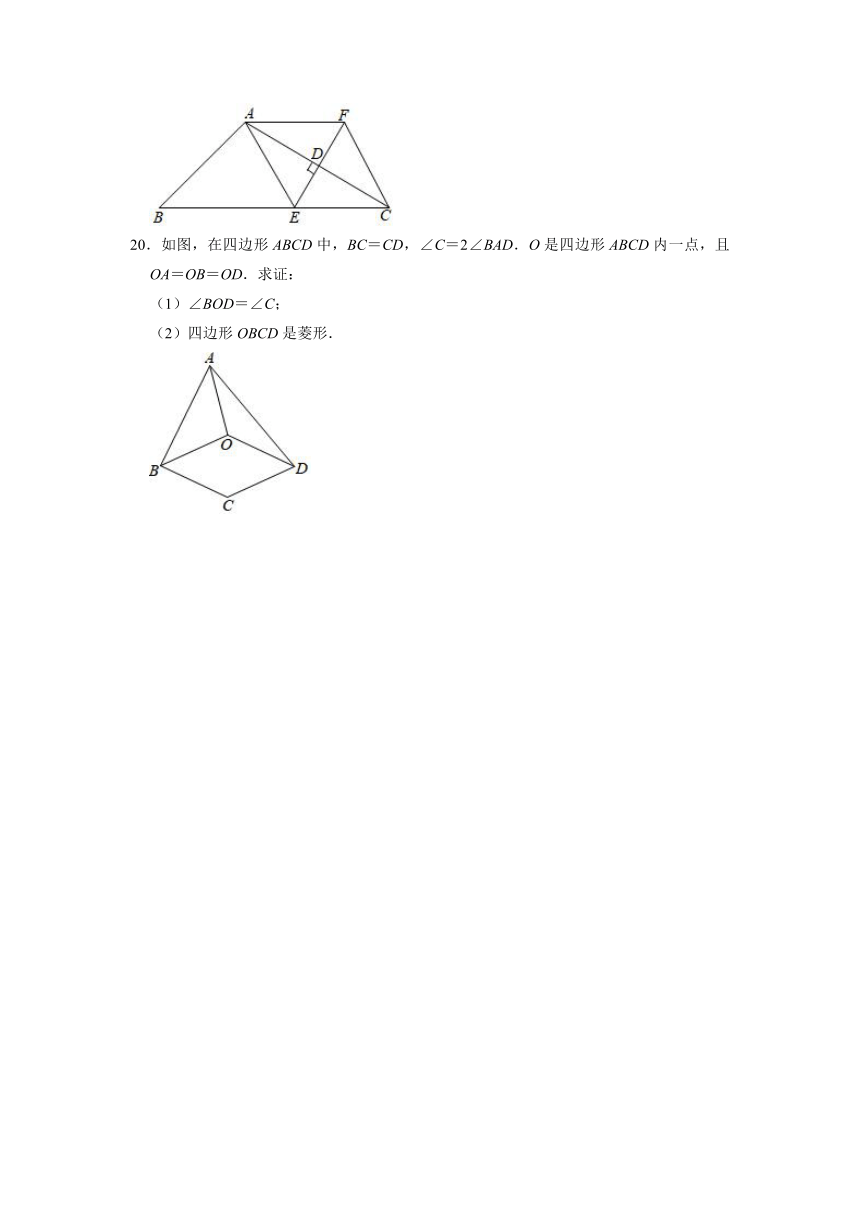
19.如图,已知△ABC中,D是AC的中点,过点D作DE⊥AC交BC于点E,过点A作AF∥BC交DE于点F,连接AE、CF.
(1)求证:四边形AECF是菱形;
(2)若CF=2,∠FAC=30°,∠B=45°,求AB的长.
20.如图,在四边形ABCD中,BC=CD,∠C=2∠BAD.O是四边形ABCD内一点,且OA=OB=OD.求证:
(1)∠BOD=∠C;
(2)四边形OBCD是菱形.
参考答案
1.解:A、∵四边形ABCD是平行四边形,
∴AB=CD,故选项A不符合题意;
B、∵四边形ABCD是平行四边形,AB=BC,
∴ ABCD为菱形,故选项B符合题意;
C、∵四边形ABCD是平行四边形,∠BAD=90°,
∴ ABCD为矩形,故选项C不符合题意;
D、∵四边形ABCD是平行四边形,AC=BD,
∴ ABCD为矩形,故选项D不符合题意;
故选:B.
2.解:∵菱形ABCD,∠BCD=120°,
∴∠ABC=60°,
∵B(﹣1,0),
∴OB=1,OA=,AB=2,
∴A(0,),
∴BC=AD=2,
∴OC=BC﹣OB=2﹣1=1,
∴C(1,0),D(2,),
故选:D.
3.解:∵四边形ABCD是菱形,
∴AD=CD=BC=AB,AC⊥BD,AO=CO,DO=BO,
∴∠AOD=∠COD=∠BOC=∠AOB=90°,
∴Rt△AOD≌Rt△COD≌Rt△BOC≌Rt△AOB(HL),即四个三角形的面积相等,
∵在菱形ABCD中,对角线AC=8,BD=10,
∴菱形ABCD的面积为:AC BD=40.
∴△AOD的面积为:40=10.
故选:B.
4.解:如图,连结BD,作DH⊥AB,垂足为H,
∵四边形ABCD是菱形,
∴AB=AD,AD∥BC,
∵∠A=60°,
∴△ABD是等边三角形,∠ABC=180°﹣∠A=120°,
∴AD=BD,∠ABD=∠A=∠ADB=60°,
∴∠DBC=∠ABC﹣∠ABD=120°﹣60°=60°,
∵AE=BF,
∴△ADE≌△BDF(SAS),
∴DE=DF,∠ADE=∠FDB,
∴∠EDF=∠EDB+∠FDB=∠EDB+∠ADE=∠ADB=60°,
∴△DEF是等边三角形,
∵△DEF的周长是3,
∴DE=,
设AH=x,则HE=2﹣x,
∵AD=BD,DH⊥AB,
∴∠ADH=∠ADB=30°,
∴AD=2x,DH=x,
在Rt△DHE中,DH +HE =DE ,
∴(x) +(2﹣x) =() ,
解得:x=(负值舍去),
∴AD=2x=1+,
故选:C.
5.解:∵四边形ABD是菱形,∠ADC=120°,
∴AD=AB=BC=CD,∠BAD=∠BCD=60°,∠DAE=∠BAE,∠DCE=∠BCE=∠BCD=30°,
∵∠BFE=∠BCE+∠CBF=30°+50°=80°,
∴∠EBF=180°﹣∠BEC﹣∠BFE=180°﹣50°﹣80°=50°,
在△CDE和△CBE中,
,
∴△CDE≌△CBE(SAS),
∴∠DEC=∠BEC=50°,
∴∠BEM=∠DEC+∠BEC=100°,
∴∠BME=180°﹣∠BEM﹣∠EBF=180°﹣100°﹣50°=30°,故①正确;
在△ADE和△ABE中,
,
∴△ADE≌△ABE(SAS),故②正确;
∵∠EBC=∠EBF+∠CBF=100°,
∴∠BEM=∠EBC,
在△BEM和△EBC中,
,
∴△BEM≌△EBC(AAS),
∴BM=EC,EM=BC,故③正确;
连接BD交AC于O,如图所示:
∵四边形ABCD是菱形,
∴OA=OC,AC⊥BD,
∵∠DCO=30°,
∴OD=CD=BC,OC=OD,
∴OC=BC,
∴AC=2OC=BC,
∵BM=EC,EM=BC,
∴AE+BM=AE+EC=AC=BC=EM,故④正确,
正确结论的个数是4个,
故选:D.
6.解:连接BP,如图,
∵四边形ABCD为菱形,菱形ABCD的周长为20,
∴BA=BC=5,S△ABC=S菱形ABCD=12,
∵S△ABC=S△PAB+S△PBC,
∴×5×PE+×5×PF=12,
∴PE+PF=,
故选:B.
7.解:如图连接AC,AD,分别交OB于G、P,作BK⊥OA于K.
∵四边形OABC是菱形,
∴AC⊥OB,GC=AG,OG=BG=2,A、C关于直线OB对称,
∴PC+PD=PA+PD=DA,
∴此时PC+PD最短,
在Rt△AOG中,AG===,
∴AC=2,
∵OA BK= AC OB,
∴BK=4,AK==3,
∴点B坐标(8,4),
∴直线OB解析式为y=x,直线AD解析式为y=﹣x+1,
由解得,
∴点P坐标(,).
故选:D.
8.解:作F点关于BD的对称点F′,连接EF′交BD于点P,则PF=PF′.
∴EP+FP=EP+F′P.
由两点之间线段最短可知:当E、P、F′在一条直线上时,EP+FP的值最小,此时EP+FP=EP+F′P=EF′.
∵四边形ABCD为菱形,周长为12,
∴AB=BC=CD=DA=3,AB∥CD,
∵AF=2,AE=1,
∴DF=DF′=AE=1,
∴四边形AEF′D是平行四边形,
∴EF′=AD=3.
∴EP+FP的最小值为3.
故选:C.
9.解:∵四边形ABCD是菱形,
∴AB=BC=CD=AD.∠A=∠BCD.
∵∠A=60°,
∴∠BCD=60°,△ABD是等边三角形,
∴△BDC是等边三角形.∠ADB=∠ABD=60°,
∴∠CDB=∠CBD=60°.
∵E,F分别是AB,AD的中点,
∴∠BFD=∠DEB=90°,
∴∠GDB=∠GBD=30°,
∴∠GDC=∠GBC=90°,DG=BG,
∴∠FGE=∠BGD=360°﹣90°﹣90°﹣60°=120°,故①正确;
在△CDG和△CBG中,,
∴△CDG≌△CBG(SSS),
∴∠DGC=∠BGC=60°.
∴∠GCD=30°,
∴CG=2GD=GD+GD,
∴CG=DG+BG.故②正确.
∵△GBC为直角三角形,
∴CG>BC,
∴CG≠BD,
∴△BDF与△CGB不全等.故③错误;
∵△ABC是等边三角形,E、F分别是AB、AD的中点,
∴△ADE的面积=△BDE的面积=△ABF的面积,
∴△DFG的面积=△BEG的面积,
∴S四边形AEGF=S△BDG,故④正确;
∴正确的有:①②④共3个.
故选:C.
10.解:四边形ADBC一定是菱形,
理由是:∵根据做法可知:AC=CB=BD=AD,
∴四边形ADBC是菱形,
故选:A.
11.解:∵四边形ABCD是菱形,
∴OA=OC=6,OB=OD,AC⊥BD,
∴AC=12,
∵DH⊥AB,
∴∠BHD=90°,
∴OH=BD,
∵菱形ABCD的面积=×AC×BD=×12×BD=48,
∴BD=8,
∴OH=BD=4;
故选:A.
12.解:A.四边相等的四边形是菱形;正确;
B.对角线垂直的平行四边形是菱形;正确;
C.∵菱形的对角线互相垂直且平分,
∴选项C不正确;
D.菱形的邻边相等;正确;
故选:C.
13.解:连接CG,过点C作CM⊥AD,交AD的延长线于M,
∵F、H分别为CE、GE中点,
∴FH是△CEG的中位线,
∴HF=CG,
∵四边形ABCD是菱形,
∴AD∥BC,AB∥CD,
∴∠DGE=∠E,
∵∠EHF=∠DGE,
∴∠E=∠EHF,
∴HF=EF=CF,
∴CG=2HF=2,
∵AB∥CD,
∴∠CDM=∠A=60°,
设DM=x,则CD=2x,CM=,
∵点G为AD的中点,
∴DG=x,
在Rt△CMG中,由勾股定理得:
CG==2,
∴x=2,
∴AB=CD=2x=4.
故答案为:4.
14.解:如图,连接AC交BD于点H,
由菱形的性质得∠BDC=35°,∠DCE=70°,
又∵∠MCE=15°,
∴∠DCF=55°,
∵DF⊥CM,
∴∠CDF=35°,
又∵四边形ABCD是菱形,
∴BD平分∠ADC,
∴∠HDC=35°,
在△CDH和△CDF中,
,
∴△CDH≌△CDF(AAS),
∴DF=DH=,
∴DB=2,
故答案为2.
15.解:如图,
∵AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形,
作AE⊥BC于点E,AF⊥DC于点F,
∵两张等宽的长方形纸条交叉叠放在一起,
∴AE=AF,
∴S平行四边形ABCD=BC AE=DC AF,
∴BC=DC,
∴ ABCD是菱形.
故答案为:是.
16.证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
又∵EF∥AB,
∴四边形ABFE是平行四边形,
∵BE平分∠ABC,
∴∠ABE=∠FBE,
∵AD∥BC,
∴∠AEB=∠EBF,
∴∠ABE=∠AEB,
∴AB=AE,
∴平行四边形ABFE是菱形.
17.证明:∵四边形ABCD是平行四边形,
∴∠BAD=∠C,AD∥BC,AB∥CD,
∵AF∥ED,
∴四边形AEDF是平行四边形,
∵AD∥BC,
∴∠DGC=∠ADE,
∵DG=DC,
∴∠DGC=∠C,
∴∠BAD=∠ADE,
∴AE=DE,
∴平行四边形AEDF是菱形.
18.证明:(1)∵四边形ABCD是菱形,
∴AB=CD,AB∥CD,
∴∠BAE=∠DCF,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(SAS);
(2)如图,连接BD,交AC于O,
∵四边形ABCD是菱形,
∴BD⊥AC,AO=CO,BO=DO,
∵AE=CF,
∴EO=FO,
∴四边形BEDF是平行四边形,
又∵BD⊥EF,
∴平行四边形BEDF是菱形.
19.解:(1)证明:如图,
在△ABC中,点D是AC的中点,
∴AD=DC,
∵AF∥BC,
∴∠FAD=∠ECD,∠AFD=∠CED,
∴△AFD≌△CED(AAS),
∴AF=EC,
∴四边形AECF是平行四边形,
又EF⊥AC,点D是AC的中点,即EF垂直平分AC,
∴AF=FC,
∴平行四边形AECF是菱形.
(2)如图,过点A作AG⊥BC于点G,
由(1)知四边形AECF是菱形,又CF=2,∠FAC=30°,
∴AF∥EC,AE=CF=2,∠FAE=2∠FAC=60°,
∴∠AEB=∠FAE=60°,
∵AG⊥BC,
∴∠AGB=∠AGE=90°,
∴∠GAE=30°,
∴GE=AE=1,AG=GE=,
∵∠B=45°,
∴∠GAB=∠B=45°,
∴BG=AG=,
∴AB=BG=.
20.证明:(1)
延长AO到E,
∵OA=OB,
∴∠ABO=∠BAO,
又∠BOE=∠ABO+∠BAO,
∴∠BOE=2∠BAO,
同理∠DOE=2∠DAO,
∴∠BOE+∠DOE=2∠BAO+2∠DAO=2(∠BAO+∠DAO)
即∠BOD=2∠BAD,
又∠C=2∠BAD,
∴∠BOD=∠C;
(2)连接OC,
∵BC=CD,OA=OB=OD,OC是公共边,
∵OB=OD,CB=CD,OC=OC,
∴△OBC≌△ODC,
∴∠BOC=∠DOC,∠BCO=∠DCO,
∵∠BOD=∠BOC+∠DOC,∠BCD=∠BCO+∠DCO,
∴∠BOC=∠BOD,∠BCO=∠BCD,
又∠BOD=∠BCD,
∴∠BOC=∠BCO,
∴BO=BC,
又OB=OD,BC=CD,
∴OB=BC=CD=DO,
∴四边形OBCD是菱形.
法二,连接OC,
∵BC=CD,OA=OB=OD,OC是公共边,
∵OB=OD,CB=CD,OC=OC,
∴△OBC≌△ODC(SSS),
∴∠B=∠D,∠BOC=∠DOC,∠BCO=∠DCO,
∴∠BOD=∠BCD,
∴四边形BCDO是平行四边形,
∵BC=CD,
∴平行四边形BCDO是菱形.
解法二:连接BD,因∠BOD=∠C;BC=CD,OB=OD,所以角OBD等于角ODB=角CBD=角CDB,可以得出两组边分别平行,从而得出OBCD是菱形
1.下列选项中能使 ABCD成为菱形的是( )
A.AB=CD B.AB=BC C.∠BAD=90° D.AC=BD
2.如图,在直角坐标系中,菱形ABCD的顶点A,B,C在坐标轴上,若点B的坐标为(﹣1,0),∠BCD=120°,则点D的坐标为( )
A.(2,2) B.(,2) C.(3,) D.(2,)
3.如图,在菱形ABCD中,对角线AC=8,BD=10,则△AOD的面积为( )
A.9 B.10 C.11 D.12
4.如图,在菱形ABCD中,∠A=60°,点E,F分别在边AB,BC上,AE=BF=2,△DEF的周长为3,则AD的长为( )
A. B.2 C.+1 D.2﹣1
5.如图,点E,F在菱形ABCD的对角线AC上,∠ADC=120°,∠BEC=∠CBF=50°,ED与BF的延长线交于点M.则对于以下结论:①∠BME=30°;②△ADE≌△ABE;③EM=BC;④AE+BM=EM.其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
6.如图,在菱形ABCD中,P是对角线AC上一动点,过点P作PE⊥BC于点E.PF⊥AB于点F.若菱形ABCD的周长为20,面积为24,则PE+PF的值为( )
A.4 B. C.6 D.
7.已知菱形OABC在平面直角坐标系的位置如图所示,顶点A(5,0),OB=4,点P是对角线OB上的一个动点,D(0,1),当CP+DP最短时,点P的坐标为( )
A.(0,0) B.(1,) C.(,) D.(,)
8.如图,在周长为12的菱形ABCD中,AE=1,AF=2,若P为对角线BD上一动点,则EP+FP的最小值为( )
A.1 B.2 C.3 D.4
9.如图,在菱形ABCD中,∠A=60°,E、F分别是AB、AD的中点DE、BF相交于点G,连接BD、CG.有下列结论:①∠FGE=120° ②BG+DG=CG③△BDF≌△CGB④S四边形AEGF=S△BDG,其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
10.如图,聪聪在作线段AB的垂直平分线时,他是这样操作的:分别以A和B为圆心,大于AB的长为半径画弧,两弧交于C、D,则直线CD即为所求.根据他的作图方法可知四边形ADBC一定是( )
A.菱形 B.矩形 C.正方形 D.等腰梯形
11.如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DH⊥AB于点H,连接OH,若OA=6,S菱形ABCD=48,则OH的长为( )
A.4 B.8 C. D.6
12.下列说法中不正确的是( )
A.四边相等的四边形是菱形
B.对角线垂直的平行四边形是菱形
C.菱形的对角线互相垂直且相等
D.菱形的邻边相等
13.如图,在菱形ABCD中,∠A=60°,G为AD中点,点E在BC延长线上,F、H分别为CE、GE中点,∠EHF=∠DGE,CF=,则AB= .
14.如图,四边形ABCD为菱形,∠ABC=70°,延长BC到E,在∠DCE内作射线CM,使得∠ECM=15°,过点D作DF⊥CM,垂足为F,若DF=,则对角线BD的长为 .(结果保留根号)
15.如图,将两张对边平行且等宽的纸条交叉叠放在一起,则重合部分构成的四边形ABCD 菱形(填“是”或“不是”).
16.已知:如图,在 ABCD中,点E、F分别在AD、BC上,且BE平分∠ABC,EF∥AB.求证:四边形ABFE是菱形.
17.如图,在 ABCD中,G为BC边上一点,DG=DC,延长DG交AB的延长线于点E,过点A作AF∥ED交CD的延长线于点F.求证:四边形AEDF是菱形.
18.如图,在菱形ABCD中,E,F是对角线AC上的两点,且AE=CF.
(1)求证:△ABE≌△CDF;
(2)求证:四边形BEDF是菱形.
19.如图,已知△ABC中,D是AC的中点,过点D作DE⊥AC交BC于点E,过点A作AF∥BC交DE于点F,连接AE、CF.
(1)求证:四边形AECF是菱形;
(2)若CF=2,∠FAC=30°,∠B=45°,求AB的长.
20.如图,在四边形ABCD中,BC=CD,∠C=2∠BAD.O是四边形ABCD内一点,且OA=OB=OD.求证:
(1)∠BOD=∠C;
(2)四边形OBCD是菱形.
参考答案
1.解:A、∵四边形ABCD是平行四边形,
∴AB=CD,故选项A不符合题意;
B、∵四边形ABCD是平行四边形,AB=BC,
∴ ABCD为菱形,故选项B符合题意;
C、∵四边形ABCD是平行四边形,∠BAD=90°,
∴ ABCD为矩形,故选项C不符合题意;
D、∵四边形ABCD是平行四边形,AC=BD,
∴ ABCD为矩形,故选项D不符合题意;
故选:B.
2.解:∵菱形ABCD,∠BCD=120°,
∴∠ABC=60°,
∵B(﹣1,0),
∴OB=1,OA=,AB=2,
∴A(0,),
∴BC=AD=2,
∴OC=BC﹣OB=2﹣1=1,
∴C(1,0),D(2,),
故选:D.
3.解:∵四边形ABCD是菱形,
∴AD=CD=BC=AB,AC⊥BD,AO=CO,DO=BO,
∴∠AOD=∠COD=∠BOC=∠AOB=90°,
∴Rt△AOD≌Rt△COD≌Rt△BOC≌Rt△AOB(HL),即四个三角形的面积相等,
∵在菱形ABCD中,对角线AC=8,BD=10,
∴菱形ABCD的面积为:AC BD=40.
∴△AOD的面积为:40=10.
故选:B.
4.解:如图,连结BD,作DH⊥AB,垂足为H,
∵四边形ABCD是菱形,
∴AB=AD,AD∥BC,
∵∠A=60°,
∴△ABD是等边三角形,∠ABC=180°﹣∠A=120°,
∴AD=BD,∠ABD=∠A=∠ADB=60°,
∴∠DBC=∠ABC﹣∠ABD=120°﹣60°=60°,
∵AE=BF,
∴△ADE≌△BDF(SAS),
∴DE=DF,∠ADE=∠FDB,
∴∠EDF=∠EDB+∠FDB=∠EDB+∠ADE=∠ADB=60°,
∴△DEF是等边三角形,
∵△DEF的周长是3,
∴DE=,
设AH=x,则HE=2﹣x,
∵AD=BD,DH⊥AB,
∴∠ADH=∠ADB=30°,
∴AD=2x,DH=x,
在Rt△DHE中,DH +HE =DE ,
∴(x) +(2﹣x) =() ,
解得:x=(负值舍去),
∴AD=2x=1+,
故选:C.
5.解:∵四边形ABD是菱形,∠ADC=120°,
∴AD=AB=BC=CD,∠BAD=∠BCD=60°,∠DAE=∠BAE,∠DCE=∠BCE=∠BCD=30°,
∵∠BFE=∠BCE+∠CBF=30°+50°=80°,
∴∠EBF=180°﹣∠BEC﹣∠BFE=180°﹣50°﹣80°=50°,
在△CDE和△CBE中,
,
∴△CDE≌△CBE(SAS),
∴∠DEC=∠BEC=50°,
∴∠BEM=∠DEC+∠BEC=100°,
∴∠BME=180°﹣∠BEM﹣∠EBF=180°﹣100°﹣50°=30°,故①正确;
在△ADE和△ABE中,
,
∴△ADE≌△ABE(SAS),故②正确;
∵∠EBC=∠EBF+∠CBF=100°,
∴∠BEM=∠EBC,
在△BEM和△EBC中,
,
∴△BEM≌△EBC(AAS),
∴BM=EC,EM=BC,故③正确;
连接BD交AC于O,如图所示:
∵四边形ABCD是菱形,
∴OA=OC,AC⊥BD,
∵∠DCO=30°,
∴OD=CD=BC,OC=OD,
∴OC=BC,
∴AC=2OC=BC,
∵BM=EC,EM=BC,
∴AE+BM=AE+EC=AC=BC=EM,故④正确,
正确结论的个数是4个,
故选:D.
6.解:连接BP,如图,
∵四边形ABCD为菱形,菱形ABCD的周长为20,
∴BA=BC=5,S△ABC=S菱形ABCD=12,
∵S△ABC=S△PAB+S△PBC,
∴×5×PE+×5×PF=12,
∴PE+PF=,
故选:B.
7.解:如图连接AC,AD,分别交OB于G、P,作BK⊥OA于K.
∵四边形OABC是菱形,
∴AC⊥OB,GC=AG,OG=BG=2,A、C关于直线OB对称,
∴PC+PD=PA+PD=DA,
∴此时PC+PD最短,
在Rt△AOG中,AG===,
∴AC=2,
∵OA BK= AC OB,
∴BK=4,AK==3,
∴点B坐标(8,4),
∴直线OB解析式为y=x,直线AD解析式为y=﹣x+1,
由解得,
∴点P坐标(,).
故选:D.
8.解:作F点关于BD的对称点F′,连接EF′交BD于点P,则PF=PF′.
∴EP+FP=EP+F′P.
由两点之间线段最短可知:当E、P、F′在一条直线上时,EP+FP的值最小,此时EP+FP=EP+F′P=EF′.
∵四边形ABCD为菱形,周长为12,
∴AB=BC=CD=DA=3,AB∥CD,
∵AF=2,AE=1,
∴DF=DF′=AE=1,
∴四边形AEF′D是平行四边形,
∴EF′=AD=3.
∴EP+FP的最小值为3.
故选:C.
9.解:∵四边形ABCD是菱形,
∴AB=BC=CD=AD.∠A=∠BCD.
∵∠A=60°,
∴∠BCD=60°,△ABD是等边三角形,
∴△BDC是等边三角形.∠ADB=∠ABD=60°,
∴∠CDB=∠CBD=60°.
∵E,F分别是AB,AD的中点,
∴∠BFD=∠DEB=90°,
∴∠GDB=∠GBD=30°,
∴∠GDC=∠GBC=90°,DG=BG,
∴∠FGE=∠BGD=360°﹣90°﹣90°﹣60°=120°,故①正确;
在△CDG和△CBG中,,
∴△CDG≌△CBG(SSS),
∴∠DGC=∠BGC=60°.
∴∠GCD=30°,
∴CG=2GD=GD+GD,
∴CG=DG+BG.故②正确.
∵△GBC为直角三角形,
∴CG>BC,
∴CG≠BD,
∴△BDF与△CGB不全等.故③错误;
∵△ABC是等边三角形,E、F分别是AB、AD的中点,
∴△ADE的面积=△BDE的面积=△ABF的面积,
∴△DFG的面积=△BEG的面积,
∴S四边形AEGF=S△BDG,故④正确;
∴正确的有:①②④共3个.
故选:C.
10.解:四边形ADBC一定是菱形,
理由是:∵根据做法可知:AC=CB=BD=AD,
∴四边形ADBC是菱形,
故选:A.
11.解:∵四边形ABCD是菱形,
∴OA=OC=6,OB=OD,AC⊥BD,
∴AC=12,
∵DH⊥AB,
∴∠BHD=90°,
∴OH=BD,
∵菱形ABCD的面积=×AC×BD=×12×BD=48,
∴BD=8,
∴OH=BD=4;
故选:A.
12.解:A.四边相等的四边形是菱形;正确;
B.对角线垂直的平行四边形是菱形;正确;
C.∵菱形的对角线互相垂直且平分,
∴选项C不正确;
D.菱形的邻边相等;正确;
故选:C.
13.解:连接CG,过点C作CM⊥AD,交AD的延长线于M,
∵F、H分别为CE、GE中点,
∴FH是△CEG的中位线,
∴HF=CG,
∵四边形ABCD是菱形,
∴AD∥BC,AB∥CD,
∴∠DGE=∠E,
∵∠EHF=∠DGE,
∴∠E=∠EHF,
∴HF=EF=CF,
∴CG=2HF=2,
∵AB∥CD,
∴∠CDM=∠A=60°,
设DM=x,则CD=2x,CM=,
∵点G为AD的中点,
∴DG=x,
在Rt△CMG中,由勾股定理得:
CG==2,
∴x=2,
∴AB=CD=2x=4.
故答案为:4.
14.解:如图,连接AC交BD于点H,
由菱形的性质得∠BDC=35°,∠DCE=70°,
又∵∠MCE=15°,
∴∠DCF=55°,
∵DF⊥CM,
∴∠CDF=35°,
又∵四边形ABCD是菱形,
∴BD平分∠ADC,
∴∠HDC=35°,
在△CDH和△CDF中,
,
∴△CDH≌△CDF(AAS),
∴DF=DH=,
∴DB=2,
故答案为2.
15.解:如图,
∵AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形,
作AE⊥BC于点E,AF⊥DC于点F,
∵两张等宽的长方形纸条交叉叠放在一起,
∴AE=AF,
∴S平行四边形ABCD=BC AE=DC AF,
∴BC=DC,
∴ ABCD是菱形.
故答案为:是.
16.证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
又∵EF∥AB,
∴四边形ABFE是平行四边形,
∵BE平分∠ABC,
∴∠ABE=∠FBE,
∵AD∥BC,
∴∠AEB=∠EBF,
∴∠ABE=∠AEB,
∴AB=AE,
∴平行四边形ABFE是菱形.
17.证明:∵四边形ABCD是平行四边形,
∴∠BAD=∠C,AD∥BC,AB∥CD,
∵AF∥ED,
∴四边形AEDF是平行四边形,
∵AD∥BC,
∴∠DGC=∠ADE,
∵DG=DC,
∴∠DGC=∠C,
∴∠BAD=∠ADE,
∴AE=DE,
∴平行四边形AEDF是菱形.
18.证明:(1)∵四边形ABCD是菱形,
∴AB=CD,AB∥CD,
∴∠BAE=∠DCF,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(SAS);
(2)如图,连接BD,交AC于O,
∵四边形ABCD是菱形,
∴BD⊥AC,AO=CO,BO=DO,
∵AE=CF,
∴EO=FO,
∴四边形BEDF是平行四边形,
又∵BD⊥EF,
∴平行四边形BEDF是菱形.
19.解:(1)证明:如图,
在△ABC中,点D是AC的中点,
∴AD=DC,
∵AF∥BC,
∴∠FAD=∠ECD,∠AFD=∠CED,
∴△AFD≌△CED(AAS),
∴AF=EC,
∴四边形AECF是平行四边形,
又EF⊥AC,点D是AC的中点,即EF垂直平分AC,
∴AF=FC,
∴平行四边形AECF是菱形.
(2)如图,过点A作AG⊥BC于点G,
由(1)知四边形AECF是菱形,又CF=2,∠FAC=30°,
∴AF∥EC,AE=CF=2,∠FAE=2∠FAC=60°,
∴∠AEB=∠FAE=60°,
∵AG⊥BC,
∴∠AGB=∠AGE=90°,
∴∠GAE=30°,
∴GE=AE=1,AG=GE=,
∵∠B=45°,
∴∠GAB=∠B=45°,
∴BG=AG=,
∴AB=BG=.
20.证明:(1)
延长AO到E,
∵OA=OB,
∴∠ABO=∠BAO,
又∠BOE=∠ABO+∠BAO,
∴∠BOE=2∠BAO,
同理∠DOE=2∠DAO,
∴∠BOE+∠DOE=2∠BAO+2∠DAO=2(∠BAO+∠DAO)
即∠BOD=2∠BAD,
又∠C=2∠BAD,
∴∠BOD=∠C;
(2)连接OC,
∵BC=CD,OA=OB=OD,OC是公共边,
∵OB=OD,CB=CD,OC=OC,
∴△OBC≌△ODC,
∴∠BOC=∠DOC,∠BCO=∠DCO,
∵∠BOD=∠BOC+∠DOC,∠BCD=∠BCO+∠DCO,
∴∠BOC=∠BOD,∠BCO=∠BCD,
又∠BOD=∠BCD,
∴∠BOC=∠BCO,
∴BO=BC,
又OB=OD,BC=CD,
∴OB=BC=CD=DO,
∴四边形OBCD是菱形.
法二,连接OC,
∵BC=CD,OA=OB=OD,OC是公共边,
∵OB=OD,CB=CD,OC=OC,
∴△OBC≌△ODC(SSS),
∴∠B=∠D,∠BOC=∠DOC,∠BCO=∠DCO,
∴∠BOD=∠BCD,
∴四边形BCDO是平行四边形,
∵BC=CD,
∴平行四边形BCDO是菱形.
解法二:连接BD,因∠BOD=∠C;BC=CD,OB=OD,所以角OBD等于角ODB=角CBD=角CDB,可以得出两组边分别平行,从而得出OBCD是菱形
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
