2021-2022学年高一上学期数学人教B版(2019)必修第三册7.4数学建模活动:周期现象的描述 同步练习
文档属性
| 名称 | 2021-2022学年高一上学期数学人教B版(2019)必修第三册7.4数学建模活动:周期现象的描述 同步练习 |

|
|
| 格式 | docx | ||
| 文件大小 | 765.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-28 00:00:00 | ||
图片预览




文档简介
北京·高一·同步练习
数学建模活动:周期现象的描述
一、小题
1.在两个弹簧上各有一个质量分别为和的小球做上下自由振动,已知它们在时间离开平衡位置的位移和分别由下列两式确定:,.当时,与的大小关系是( )
A. B. C. D.不能确定
2.如图为一半径为的水轮,水轮圆心距水面,已知水轮每分钟转圈,水轮上的点到水面距离与时间满足关系式,则有( )
A., B.,
C., D.,
3.据市场调查,某种商品一年内每件出厂价在7千元的基础上,按月呈的模型波动(x为月份),已知3月份达到最高价9千元,7月份价格最低为5千元,根据以上条件可确定的解析式为
A.
B.
C.
D.
4.车流量被定义为单位时间内通过十字路口的车辆数,单位为辆/分钟.若上班高峰期某十字路口的车流量(单位:辆/分钟)与时间(单位:分钟)的函数关系式为,则下列哪个时间段内车流量是增加的( )
A. B. C. D.
5.某巨型摩天轮.其旋转半径50米,最高点距地面110米,运行一周大约21分钟.某人在最低点的位置坐上摩天轮,则第35分钟时他距地面大约为米.
A.75 B.85 C.100 D.110
6.一半径为的水轮如图所示,水轮圆心距离水面,已知水轮每逆时针转动一圈,如果当水轮上点从水中浮现时(图中点)开始计时,则( )
A.点第一次到达最高点需要
B.在水轮转动的一圈内,点距离水面的高度不低于共有的时间
C.点距离水面的距离(单位:)与时间(单位:)的函数解析式为
D.当水轮转动时,点在水面下方,距离水面
7.如图某地夏天从8~14时用电量变化曲线近似满足函数y=Asin(ωx+φ)+b.
(1)这一天的最大用电量为_____万度,最小用电量为____万度;
(2)这段曲线的函数解析式为______________.
8.某城市一年中个月的平均气温与月份的关系可近似地用三角函数来表示.已知月份的平均气温最高,为℃,月份的月平均气温最低,为℃,则月份的平均气温为______℃.
二、解答题(共7小题)
9.交流电的电压(单位:)与时间(单位:)的关系可用来表示,求:
(1)开始时的电压;
(2)电压值重复出现一次的最短时间间隔;
(3)电压的最大值和第一次获得最大值的时间.
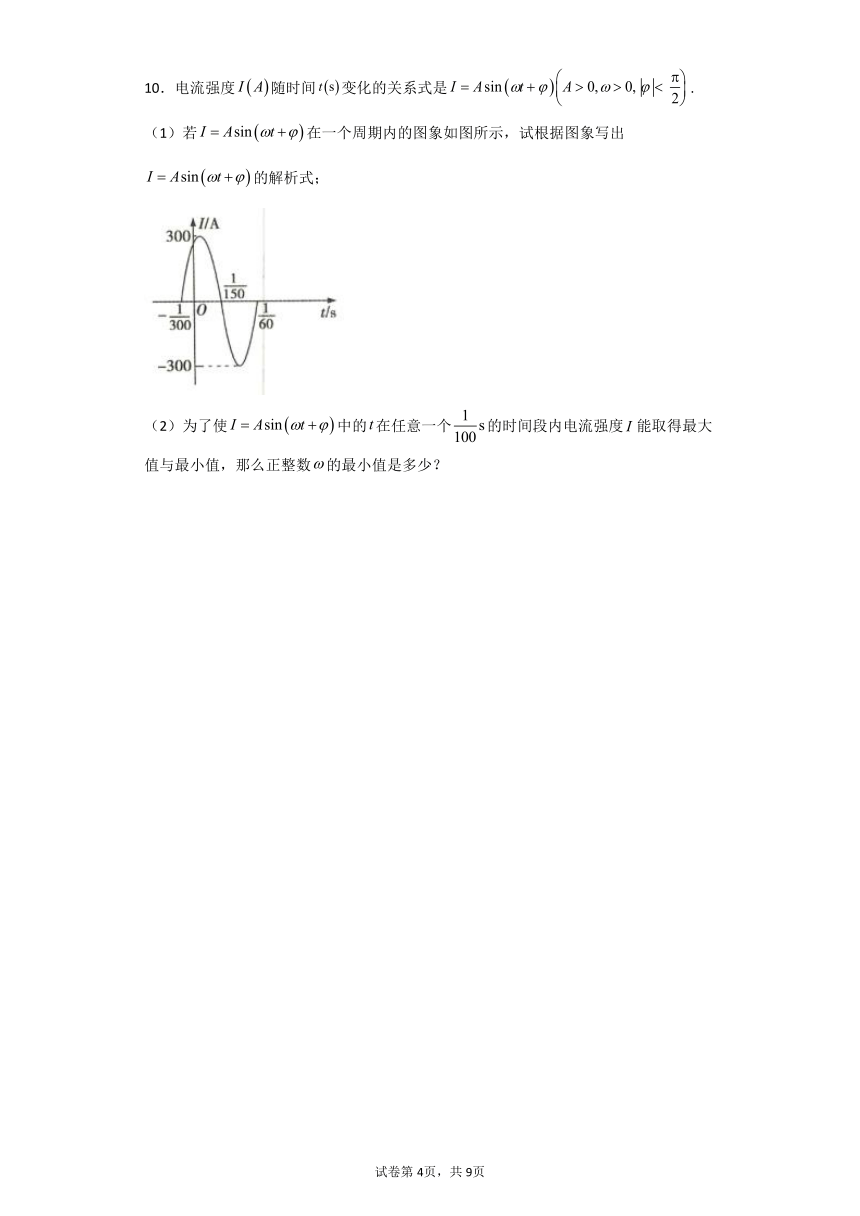
10.电流强度随时间变化的关系式是.
(1)若在一个周期内的图象如图所示,试根据图象写出的解析式;
(2)为了使中的在任意一个的时间段内电流强度能取得最大值与最小值,那么正整数的最小值是多少?
11.一个半径为2米的水轮如图所示,其圆心O距离水面1米,已知水轮按逆时针匀速转动,每4秒转一圈,如果当水轮上点P从水中浮现时(图中点)开始计算时间.
(1)以过点O且与水面垂直的直线为y轴,过点O且平行于水轮所在平面与水面的交线的直线为x轴,建立如图所示的直角坐标系,试将点P距离水面的高度h(单位:米)表示为时间t(单位:秒)的函数;
(2)在水轮转动的任意一圈内,有多长时间点P距水面的高度超过2米?
12.已知某地一天从时的温度变化曲线近似满足函数.
(1)求该地区这一段时间内温度的最大温差.
(2)若有一种细菌在到之间可以生存,则在这段时间内,该细菌最多能存活多长时间?
13.当我们所处的北半球为冬季的时候,新西兰的惠灵顿市恰好是盛夏,因此北半球的人们冬天愿意去那里旅游,下面是一份惠灵顿机场提供的月平均气温统计表.
(月份) 1 2 3 4 5 6 7 8 9 10 11 12
17.3 17.9 17.3 15.8 13.7 11.6 10.06 9.5 10.06 11.6 13.7 15.8
(1)根据这个统计表提供的数据,为惠灵顿市的月平均气温作出一个函数模型;
(2)当自然气温不低于13.7℃时,惠灵顿市最适宜旅游,试根据你所确定的函数模型,确定惠灵顿市的最佳旅游时间.
14.随着人们物质和文化生活水平的提高,旅游业也逐渐兴旺起来.经过调查研究,在某个风景区,每年到访的游客人数会发生周期性的变化.现假设该风景区每年各个月份游客的人数(单位:万人)可近似地用函数来刻画.其中:正整数表示月份且,例如时表示二月份;和是正整数;.统计发现,风景区每年各个月份游客人数有以下规律:
①每一年相同的月份,该风景区游客人数大致相同;
②该景区游客人数最多的八月份和最少的二月份相差约人;
③二月份该风景区游客大约为人,随后逐渐增加,八月份达到最多.
(1)试根据已知信息,确定一个符合条件的的表达式;
(2)一般地,当该地区游客超过人时,该风景区也进入了一年中的旅游“旺季”.那么,一年中的哪几个月是该风景区的旅游“旺季”?请说明理由.
15.为了迎接旅游旺季的到来,少林寺设置了一个专门安排旅客住宿的客栈,寺庙的工作人员发现为游客准备的食物有些月份剩余不少,浪费很严重,为了控制经营成本,减少浪费,就想适时调整投入.为此他们统计每个月入住的游客人数,发现每年各个月份来客栈入住的游客人数会呈现周期性的变化,并且有以下规律:
①每年相同的月份,入住客栈的游客人数基本相同;
②入住客栈的游客人数在月份最少,在月份最多,相差约人;
③月份入住客栈的游客约为人,随后逐月增加直到月份达到最多.
(1)试用一个正弦型三角函数描述一年中入住客栈的游客人数与月份之间的关系;
(2)请问哪几个月份要准备份以上的食物?
试卷第2页,共5页
试卷第9页,共9页
参考答案
1.C
【分析】
将分别代入与,可得.
【详解】
当时,,,所以.
故选:C
【点睛】
本题考查三角函数的应用,求三角函数的值,属于基础题.
2.B
【分析】
根据题意可得出的值,以及该函数的最小正周期,利用周期公式可求得的值,进而得出结论.
【详解】
由题意可知,可得,该函数的周期为,
.
故选:B.
【点睛】
本题考查三角函数解析式中参数的计算,考查计算能力,属于基础题.
3.A
【分析】
利用最高点和最低点可得周期及的大小,再利用最高点的坐标可得, 从而得到的解析式.
【详解】
因为3月份达到最高价9千元,7月份价格最低为5千元,所以半周期,
故,所以,
又,所以 ,
所以,
当时,,,.
,故选A.
【点睛】
已知的图像,求其解析式时可遵循“两看一算”,“两看”指从题设中得到振幅和周期,“一算”指利用最高点或最低点的坐标计算.
4.C
【分析】
由题意可知,问题是求函数在上的单调递增区间的子集,即先求出该函数在上的增区间,与取交集,并判断每个选项中的区间与单调增区间的包含关系即可得出合适选项.
【详解】
令,.
,当时,函数的单调递增区间为,当时,函数的单调递增区间为.
,车流量在时间段内是增加的,
故选:C.
【点睛】
本题考查三角函数的实际应用,将问题转化为三角函数的单调性是解答的关键,考查分析问题和解决问题的能力,属于中等题.
5.B
【详解】
分析:设出P与地面高度与时间t的关系,f(t)=Asin(ωt+φ)+B,由题意求出三角函数中的参数A,B,及周期T,利用三角函数的周期公式求出ω,通过初始位置求出φ,求出f(35)的值即可.
详解:设P与地面高度与时间t的关系,f(t)=Asin(ωt+φ)+B(A>0,ω>0,φ∈[0,2π)),
由题意可知:A=50,B=110﹣50=60,T==21,∴ω=,
即 f(t)=50sin(t+φ)+60,
又因为f(0)=110﹣100=10,即sinφ=﹣1,故φ=,
∴f(t)=50sin(t+)+60,
∴f(35)=50sin(×35+)+60=85.
故选B.
点睛:已知函数的图象求解析式
(1).
(2)由函数的周期求
(3)利用“五点法”中相对应的特殊点求,一般用最高点或最低点求.
6.D
【分析】
根据所给条件求出点距离水面的高度与时间的函数关系式,再逐项进行计算并判断作答.
【详解】
显然点距离水面的高度(米)与(秒)的关系成周期性,符合正弦型函数关系,设其解析式为,
依题意,,,由,解得,即,
当时,,得,,,
于是得所求的函数关系式是,
所以点距离水面的距离(单位:)与时间(单位:)的函数解析式为
,C错误;
由得:,即,解得,
点第一次到达最高点要时间,A错误;
由,
即在水轮转动的一圈内,有20秒的时间,点距离水面的高度不低于4.8米,B错误;
时,,D正确.
故选:D
7.50 30
【分析】
根据图象可得最值以及振幅、周期,利用最低点可求初相位,从而可得解析式.
【详解】
由图知,最大用电量为50,最小用电量为30,
故,所以,
又由图象可得半周期为,,故,
又时,,∴ ,∴.
故.
故答案:50,30,.
8.
【分析】
根据题意列出方程组,求出,求出年中12个月的平均气温与月份的三角函数关系,将代入求出10月份的平均气温值.
【详解】
据题意得,
解得,
所以
令得.
故答案为:20.5
【点睛】
本题考查通过待定系数法求出三角函数的解析式,根据解析式求函数值,意在考查学生对这些知识的理解掌握水平.
9.(1)(2).(3)
【分析】
(1)代入求解即可.
(2)电压值重复出现一次的最短时间间隔即为求解最小正周期.
(3)由题意令再求解即可.
【详解】
(1)当时,,即开始时的电压为.
(2)最小正周期,即时间间隔为.
(3)电压的最大值为,当时,,即第一次取得最大值的时间为第.
【点睛】
本题主要考查了三角函数的实际运用,属于基础题.
10.(1); (2)629.
【分析】
(1)根据最值求,求,最后代入五点中的求;(2)根据已知可知,根据不等式求的范围和最小值.
【详解】
(1)由图,可知.
,,.
将点代入解析式,得,,
,.
,,.
(2)由题意,知,,
正整数的最小值为629.
【点睛】
本题考查根据三角函数的图象求函数解析式,以及根据函数周期求参数的取值范围,根据的图象求函数的解析式,一般求解方法是根据最大值和最小值列方程组, ,求,根据图象零点或极值点之间的长度得到函数的周期,求,最后代入五点中的一个点求.
11.(1);(2)秒.
【分析】
(1)设,根据题意求得、的值,以及函数的最小正周期,可求得的值,根据的大小可得出的值,由此可得出关于的函数解析式;
(2)由得出,令,求得的取值范围,进而可解不等式,可得出的取值范围,进而得解.
【详解】
解:(1)如图所示,标出点M与点N,设,
根据题意可知,,所以,
根据函数的物理意义可知:
,
又因为函数的最小正周期为,
所以,
所以可得:.
(2)根据题意可知,,即,
当水轮转动一圈时,,可得:,
所以此时,
解得:,
又因为(秒),即水轮转动任意一圈内,有秒的时间点P距水面的高度超过2米.
12.(1)20;(2)(小时).
【分析】
(1)利用三角函数的性质求函数在的最大值与最小值可得最大温差.
(2)令,解不等式,确定解在的区间长度.
【详解】
(1)由函数易知,当函数取得最大值时 ,解得,又,所以当时,函数取得最大值,此时最高温度为,当函数取得最小值时 ,解得,当时,函数取得最小值,此时最低温度为,所以最大温差为.
(2)解法1:令,得,因为,所以.
令,得.因为,所以.
故该细菌能存活的最长时间为(小时).
解法2:令,,
,即,,
又,取得,故该细菌能存活的最长时间为.
【点睛】
本题考查三角函数的性质及应用,利用三角函数图像及周期性解简单三角不等式,考查运算求解能力,属于中档题.
13.(1);(2)每年的十一月初至第二年的四月末
【分析】
(1)作出散点图,得到曲线后,根据周期变化特点可考虑用余弦型函数模型;结合图象可求得解析式;
(2)令可求得的取值,从而可确定最佳旅游时间.
【详解】
(1)以月份为横轴,气温为纵轴作出散点图,并以光滑的曲线连接各散点,得到如图所示的曲线
由于各地月平均气温是以个月为周期变化的,故依散点图所绘制的图象,可以考虑用来模拟
由最高气温为,最低气温为得:,
又
又时,y取最大值,则
为惠灵顿市的常年气温函数模型
(2)当时,或
说明在每年的十一月初至第二年的四月末气温不低于,是惠灵顿市的最佳旅游时间
【点睛】
本题考查三角函数的实际应用问题,关键是能够建立起合适的函数模型,进而通过三角函数图象求解析式的方法求得拟合的函数模型.
14.(1);(2)一年中的四个月是该风景区的旅游“旺季”.
【分析】
(1)由实际问题的周期性且周期为、淡旺季数据,结合数学模型即可求,,进而可得表达式;
(2)由(1)结合已知条件即可求出的范围,结合实际条件即可知旺季所含月份.
【详解】
(1)根据三条规律,可知该函数为周期函数且周期为,可得,即,
由规律②③可知,,解得:
综上可得,.
(2)由条件,,可得
∴,即
又,所以,,故:,即一年中的四个月是该风景区的旅游“旺季”.
【点睛】
本题考查了三角函数的实际应用,应用已知数据求数学模型,并利用模型求参数范围,属于中档题.
15.(1);(2)月、月、月、月、月个月份.
【分析】
(1)根据①,可知函数的最小正周期是;根据②可知,最小,最大,且;根据③可知,函数在上单调递增,且,由此可得函数的解析式;
(2)由条件知,结合,,即可得到结论.
【详解】
(1)设该函数为,
根据条件①,可知这个函数的周期是;
由②可知,最小,最大,且;
由③可知,函数在上单调递增,且,所以.
根据上述分析可得,,故,且,解得.
根据分析可知,当时,取最小值,当时,取最大值.
故,且,又因为,故.
所以入住客栈的游客人数与月份之间的关系式为;
(2)令,化简得,
即,解得.
因为,且,所以、、、、,
即在月、月、月、月、月个月份要准备份以上的食物.
【点睛】
本题主要考查了在实际问题中建立三角函数模型的问题.解题的技巧是从问题中发现周期变化的规律,并将所发现的规律抽象为恰当的三角函数模型.
北京·高一·
数学建模活动:周期现象的描述
一、小题
1.在两个弹簧上各有一个质量分别为和的小球做上下自由振动,已知它们在时间离开平衡位置的位移和分别由下列两式确定:,.当时,与的大小关系是( )
A. B. C. D.不能确定
2.如图为一半径为的水轮,水轮圆心距水面,已知水轮每分钟转圈,水轮上的点到水面距离与时间满足关系式,则有( )
A., B.,
C., D.,
3.据市场调查,某种商品一年内每件出厂价在7千元的基础上,按月呈的模型波动(x为月份),已知3月份达到最高价9千元,7月份价格最低为5千元,根据以上条件可确定的解析式为
A.
B.
C.
D.
4.车流量被定义为单位时间内通过十字路口的车辆数,单位为辆/分钟.若上班高峰期某十字路口的车流量(单位:辆/分钟)与时间(单位:分钟)的函数关系式为,则下列哪个时间段内车流量是增加的( )
A. B. C. D.
5.某巨型摩天轮.其旋转半径50米,最高点距地面110米,运行一周大约21分钟.某人在最低点的位置坐上摩天轮,则第35分钟时他距地面大约为米.
A.75 B.85 C.100 D.110
6.一半径为的水轮如图所示,水轮圆心距离水面,已知水轮每逆时针转动一圈,如果当水轮上点从水中浮现时(图中点)开始计时,则( )
A.点第一次到达最高点需要
B.在水轮转动的一圈内,点距离水面的高度不低于共有的时间
C.点距离水面的距离(单位:)与时间(单位:)的函数解析式为
D.当水轮转动时,点在水面下方,距离水面
7.如图某地夏天从8~14时用电量变化曲线近似满足函数y=Asin(ωx+φ)+b.
(1)这一天的最大用电量为_____万度,最小用电量为____万度;
(2)这段曲线的函数解析式为______________.
8.某城市一年中个月的平均气温与月份的关系可近似地用三角函数来表示.已知月份的平均气温最高,为℃,月份的月平均气温最低,为℃,则月份的平均气温为______℃.
二、解答题(共7小题)
9.交流电的电压(单位:)与时间(单位:)的关系可用来表示,求:
(1)开始时的电压;
(2)电压值重复出现一次的最短时间间隔;
(3)电压的最大值和第一次获得最大值的时间.
10.电流强度随时间变化的关系式是.
(1)若在一个周期内的图象如图所示,试根据图象写出的解析式;
(2)为了使中的在任意一个的时间段内电流强度能取得最大值与最小值,那么正整数的最小值是多少?
11.一个半径为2米的水轮如图所示,其圆心O距离水面1米,已知水轮按逆时针匀速转动,每4秒转一圈,如果当水轮上点P从水中浮现时(图中点)开始计算时间.
(1)以过点O且与水面垂直的直线为y轴,过点O且平行于水轮所在平面与水面的交线的直线为x轴,建立如图所示的直角坐标系,试将点P距离水面的高度h(单位:米)表示为时间t(单位:秒)的函数;
(2)在水轮转动的任意一圈内,有多长时间点P距水面的高度超过2米?
12.已知某地一天从时的温度变化曲线近似满足函数.
(1)求该地区这一段时间内温度的最大温差.
(2)若有一种细菌在到之间可以生存,则在这段时间内,该细菌最多能存活多长时间?
13.当我们所处的北半球为冬季的时候,新西兰的惠灵顿市恰好是盛夏,因此北半球的人们冬天愿意去那里旅游,下面是一份惠灵顿机场提供的月平均气温统计表.
(月份) 1 2 3 4 5 6 7 8 9 10 11 12
17.3 17.9 17.3 15.8 13.7 11.6 10.06 9.5 10.06 11.6 13.7 15.8
(1)根据这个统计表提供的数据,为惠灵顿市的月平均气温作出一个函数模型;
(2)当自然气温不低于13.7℃时,惠灵顿市最适宜旅游,试根据你所确定的函数模型,确定惠灵顿市的最佳旅游时间.
14.随着人们物质和文化生活水平的提高,旅游业也逐渐兴旺起来.经过调查研究,在某个风景区,每年到访的游客人数会发生周期性的变化.现假设该风景区每年各个月份游客的人数(单位:万人)可近似地用函数来刻画.其中:正整数表示月份且,例如时表示二月份;和是正整数;.统计发现,风景区每年各个月份游客人数有以下规律:
①每一年相同的月份,该风景区游客人数大致相同;
②该景区游客人数最多的八月份和最少的二月份相差约人;
③二月份该风景区游客大约为人,随后逐渐增加,八月份达到最多.
(1)试根据已知信息,确定一个符合条件的的表达式;
(2)一般地,当该地区游客超过人时,该风景区也进入了一年中的旅游“旺季”.那么,一年中的哪几个月是该风景区的旅游“旺季”?请说明理由.
15.为了迎接旅游旺季的到来,少林寺设置了一个专门安排旅客住宿的客栈,寺庙的工作人员发现为游客准备的食物有些月份剩余不少,浪费很严重,为了控制经营成本,减少浪费,就想适时调整投入.为此他们统计每个月入住的游客人数,发现每年各个月份来客栈入住的游客人数会呈现周期性的变化,并且有以下规律:
①每年相同的月份,入住客栈的游客人数基本相同;
②入住客栈的游客人数在月份最少,在月份最多,相差约人;
③月份入住客栈的游客约为人,随后逐月增加直到月份达到最多.
(1)试用一个正弦型三角函数描述一年中入住客栈的游客人数与月份之间的关系;
(2)请问哪几个月份要准备份以上的食物?
试卷第2页,共5页
试卷第9页,共9页
参考答案
1.C
【分析】
将分别代入与,可得.
【详解】
当时,,,所以.
故选:C
【点睛】
本题考查三角函数的应用,求三角函数的值,属于基础题.
2.B
【分析】
根据题意可得出的值,以及该函数的最小正周期,利用周期公式可求得的值,进而得出结论.
【详解】
由题意可知,可得,该函数的周期为,
.
故选:B.
【点睛】
本题考查三角函数解析式中参数的计算,考查计算能力,属于基础题.
3.A
【分析】
利用最高点和最低点可得周期及的大小,再利用最高点的坐标可得, 从而得到的解析式.
【详解】
因为3月份达到最高价9千元,7月份价格最低为5千元,所以半周期,
故,所以,
又,所以 ,
所以,
当时,,,.
,故选A.
【点睛】
已知的图像,求其解析式时可遵循“两看一算”,“两看”指从题设中得到振幅和周期,“一算”指利用最高点或最低点的坐标计算.
4.C
【分析】
由题意可知,问题是求函数在上的单调递增区间的子集,即先求出该函数在上的增区间,与取交集,并判断每个选项中的区间与单调增区间的包含关系即可得出合适选项.
【详解】
令,.
,当时,函数的单调递增区间为,当时,函数的单调递增区间为.
,车流量在时间段内是增加的,
故选:C.
【点睛】
本题考查三角函数的实际应用,将问题转化为三角函数的单调性是解答的关键,考查分析问题和解决问题的能力,属于中等题.
5.B
【详解】
分析:设出P与地面高度与时间t的关系,f(t)=Asin(ωt+φ)+B,由题意求出三角函数中的参数A,B,及周期T,利用三角函数的周期公式求出ω,通过初始位置求出φ,求出f(35)的值即可.
详解:设P与地面高度与时间t的关系,f(t)=Asin(ωt+φ)+B(A>0,ω>0,φ∈[0,2π)),
由题意可知:A=50,B=110﹣50=60,T==21,∴ω=,
即 f(t)=50sin(t+φ)+60,
又因为f(0)=110﹣100=10,即sinφ=﹣1,故φ=,
∴f(t)=50sin(t+)+60,
∴f(35)=50sin(×35+)+60=85.
故选B.
点睛:已知函数的图象求解析式
(1).
(2)由函数的周期求
(3)利用“五点法”中相对应的特殊点求,一般用最高点或最低点求.
6.D
【分析】
根据所给条件求出点距离水面的高度与时间的函数关系式,再逐项进行计算并判断作答.
【详解】
显然点距离水面的高度(米)与(秒)的关系成周期性,符合正弦型函数关系,设其解析式为,
依题意,,,由,解得,即,
当时,,得,,,
于是得所求的函数关系式是,
所以点距离水面的距离(单位:)与时间(单位:)的函数解析式为
,C错误;
由得:,即,解得,
点第一次到达最高点要时间,A错误;
由,
即在水轮转动的一圈内,有20秒的时间,点距离水面的高度不低于4.8米,B错误;
时,,D正确.
故选:D
7.50 30
【分析】
根据图象可得最值以及振幅、周期,利用最低点可求初相位,从而可得解析式.
【详解】
由图知,最大用电量为50,最小用电量为30,
故,所以,
又由图象可得半周期为,,故,
又时,,∴ ,∴.
故.
故答案:50,30,.
8.
【分析】
根据题意列出方程组,求出,求出年中12个月的平均气温与月份的三角函数关系,将代入求出10月份的平均气温值.
【详解】
据题意得,
解得,
所以
令得.
故答案为:20.5
【点睛】
本题考查通过待定系数法求出三角函数的解析式,根据解析式求函数值,意在考查学生对这些知识的理解掌握水平.
9.(1)(2).(3)
【分析】
(1)代入求解即可.
(2)电压值重复出现一次的最短时间间隔即为求解最小正周期.
(3)由题意令再求解即可.
【详解】
(1)当时,,即开始时的电压为.
(2)最小正周期,即时间间隔为.
(3)电压的最大值为,当时,,即第一次取得最大值的时间为第.
【点睛】
本题主要考查了三角函数的实际运用,属于基础题.
10.(1); (2)629.
【分析】
(1)根据最值求,求,最后代入五点中的求;(2)根据已知可知,根据不等式求的范围和最小值.
【详解】
(1)由图,可知.
,,.
将点代入解析式,得,,
,.
,,.
(2)由题意,知,,
正整数的最小值为629.
【点睛】
本题考查根据三角函数的图象求函数解析式,以及根据函数周期求参数的取值范围,根据的图象求函数的解析式,一般求解方法是根据最大值和最小值列方程组, ,求,根据图象零点或极值点之间的长度得到函数的周期,求,最后代入五点中的一个点求.
11.(1);(2)秒.
【分析】
(1)设,根据题意求得、的值,以及函数的最小正周期,可求得的值,根据的大小可得出的值,由此可得出关于的函数解析式;
(2)由得出,令,求得的取值范围,进而可解不等式,可得出的取值范围,进而得解.
【详解】
解:(1)如图所示,标出点M与点N,设,
根据题意可知,,所以,
根据函数的物理意义可知:
,
又因为函数的最小正周期为,
所以,
所以可得:.
(2)根据题意可知,,即,
当水轮转动一圈时,,可得:,
所以此时,
解得:,
又因为(秒),即水轮转动任意一圈内,有秒的时间点P距水面的高度超过2米.
12.(1)20;(2)(小时).
【分析】
(1)利用三角函数的性质求函数在的最大值与最小值可得最大温差.
(2)令,解不等式,确定解在的区间长度.
【详解】
(1)由函数易知,当函数取得最大值时 ,解得,又,所以当时,函数取得最大值,此时最高温度为,当函数取得最小值时 ,解得,当时,函数取得最小值,此时最低温度为,所以最大温差为.
(2)解法1:令,得,因为,所以.
令,得.因为,所以.
故该细菌能存活的最长时间为(小时).
解法2:令,,
,即,,
又,取得,故该细菌能存活的最长时间为.
【点睛】
本题考查三角函数的性质及应用,利用三角函数图像及周期性解简单三角不等式,考查运算求解能力,属于中档题.
13.(1);(2)每年的十一月初至第二年的四月末
【分析】
(1)作出散点图,得到曲线后,根据周期变化特点可考虑用余弦型函数模型;结合图象可求得解析式;
(2)令可求得的取值,从而可确定最佳旅游时间.
【详解】
(1)以月份为横轴,气温为纵轴作出散点图,并以光滑的曲线连接各散点,得到如图所示的曲线
由于各地月平均气温是以个月为周期变化的,故依散点图所绘制的图象,可以考虑用来模拟
由最高气温为,最低气温为得:,
又
又时,y取最大值,则
为惠灵顿市的常年气温函数模型
(2)当时,或
说明在每年的十一月初至第二年的四月末气温不低于,是惠灵顿市的最佳旅游时间
【点睛】
本题考查三角函数的实际应用问题,关键是能够建立起合适的函数模型,进而通过三角函数图象求解析式的方法求得拟合的函数模型.
14.(1);(2)一年中的四个月是该风景区的旅游“旺季”.
【分析】
(1)由实际问题的周期性且周期为、淡旺季数据,结合数学模型即可求,,进而可得表达式;
(2)由(1)结合已知条件即可求出的范围,结合实际条件即可知旺季所含月份.
【详解】
(1)根据三条规律,可知该函数为周期函数且周期为,可得,即,
由规律②③可知,,解得:
综上可得,.
(2)由条件,,可得
∴,即
又,所以,,故:,即一年中的四个月是该风景区的旅游“旺季”.
【点睛】
本题考查了三角函数的实际应用,应用已知数据求数学模型,并利用模型求参数范围,属于中档题.
15.(1);(2)月、月、月、月、月个月份.
【分析】
(1)根据①,可知函数的最小正周期是;根据②可知,最小,最大,且;根据③可知,函数在上单调递增,且,由此可得函数的解析式;
(2)由条件知,结合,,即可得到结论.
【详解】
(1)设该函数为,
根据条件①,可知这个函数的周期是;
由②可知,最小,最大,且;
由③可知,函数在上单调递增,且,所以.
根据上述分析可得,,故,且,解得.
根据分析可知,当时,取最小值,当时,取最大值.
故,且,又因为,故.
所以入住客栈的游客人数与月份之间的关系式为;
(2)令,化简得,
即,解得.
因为,且,所以、、、、,
即在月、月、月、月、月个月份要准备份以上的食物.
【点睛】
本题主要考查了在实际问题中建立三角函数模型的问题.解题的技巧是从问题中发现周期变化的规律,并将所发现的规律抽象为恰当的三角函数模型.
北京·高一·
