3.2 一元一次方程的应用 课后综合练 2021-2022学年沪科版七年级数学上册(word版含答案)
文档属性
| 名称 | 3.2 一元一次方程的应用 课后综合练 2021-2022学年沪科版七年级数学上册(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-28 07:50:30 | ||
图片预览




文档简介
3.2一元一次方程的应用【课后综合练】
-2021-2022学年七年级数学上册(沪科版)
一、选择题
1、王芳和李丽同时采摘樱桃,王芳平均每小时采摘,李丽平均每小时采摘.采摘结束后,王芳从她采摘的樱桃中取出给了李丽,这时两人的樱桃一样多.她们采摘用了多长时间?设她们采摘所用时间为小时,下列方程正确的是( )
A. B.
C. D.
2、某商品的进价是1528元,按商品标价的八折出售时,利润是12%,如果设商品的标价为x元,那么可列出正确的方程是( )
A. B.
C. D.
3、一项工程甲单独做要40天完成,乙单独做需要50天完成.如果甲先单独做4天,然后两人合作天完成这项工程,则可列的方程正确的是( )
A. B. C. D.
4、某校教师举行茶话会.若每桌坐10人,则空出一张桌子;若每桌坐8人,还有6人不能就坐.设该校准备的桌子数为x,则可列方程为( )
A.10(x﹣1)=8x﹣6 B.10(x﹣1)=8x+6
C.10(x+1)=8x﹣6 D.10(x+1)=8x+6
5、一个两位数的十位数字与个位数字的和是9.如果把这个两位数加上63,那么恰好成为原两位数的个位数字与十位数字对调后组成的两位数,则原两位数是( ).
A.18 B.27 C.36 D.45
6、已知某商店有两件进价不同的运动衫都卖了160元,其中一件盈利60%,另一件亏损20%,在这次买卖 中这家商店( )
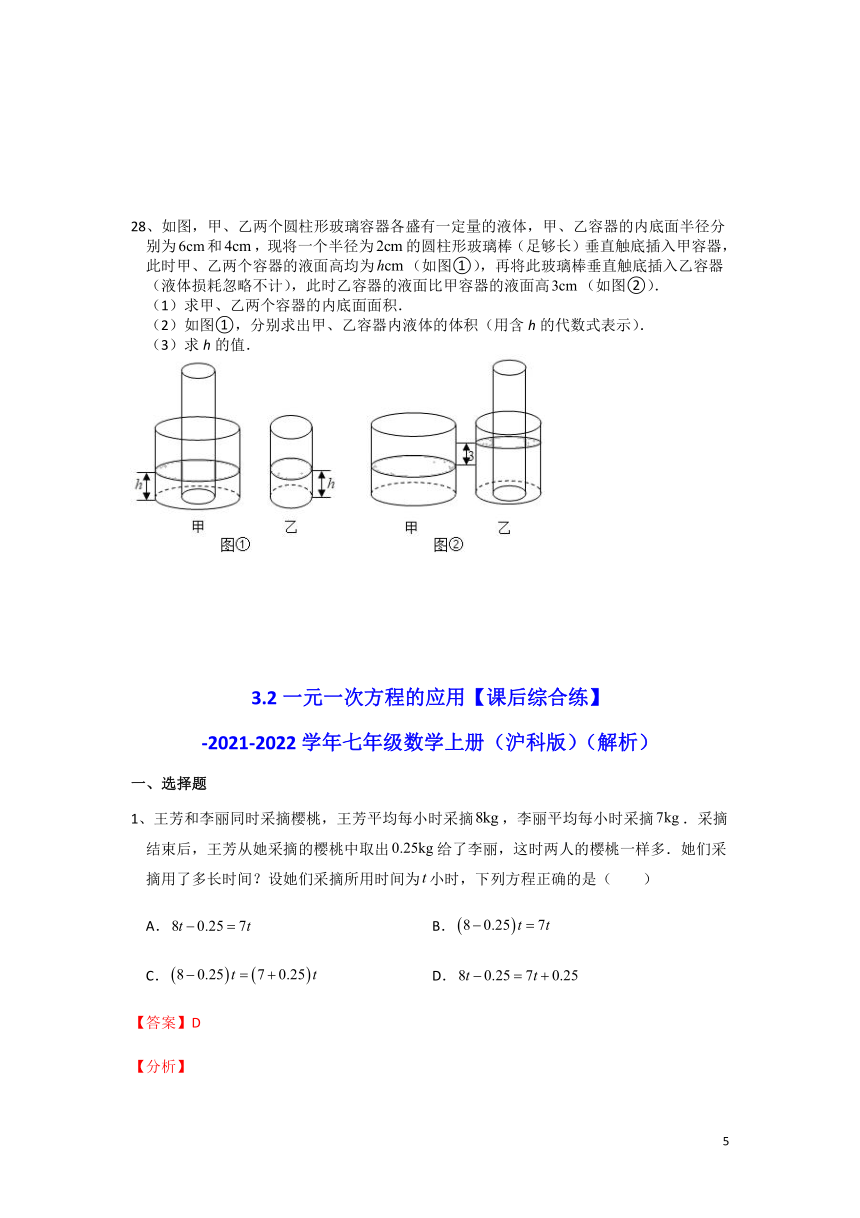
A.不盈不亏 B.盈利20元 C.盈利10元 D.亏损20元
7、一份数学试卷,有25道选择题,做对一道题得4分,做错一道题倒扣1分,某同学做了全部试题,得了80分,他共做对了( )
A.18道 B.19道 C.20道 D.21道
8、-2021年中考数学一轮复习讲练测(北京))如图是某月的月历,用形如“十”字型框任意框出5个数.对于任何一个月的月历,这5个数的和不可能是( )
A.125 B.115 C.110 D.40
9、《孙子算经》中有这样一道题,原文如下:今有百鹿入城,家取一鹿,不尽,又三家共一鹿,适尽.问:城中家几何?大意为:今有100头鹿进城,每家取一头鹿,没有取完,剩下的每3家共取一头,恰好取完.问城中有多少户人家?( )
A.55户 B.65户 C.75户 D.85户
10、一天早上,小宇从家出发去上学.小宇在离家800米时,突然想起班级今天要进行建党100周年合唱彩排,表演的衣服忘了,于是小宇立即打电话通知妈妈送来,自己则一直保持原来的速度继续赶往学校,妈妈接到电话后,马上拿起衣服以180米/分的速度沿相同的路线追赶小宇,10分钟后追上了小宇,把衣服给小宇后又立即以原速原路返回,小宇拿到衣服后继续原速赶往学校(打接电话、拿取衣服等时间都忽略不计).当小宇妈妈回到家中时,恰好小宇也刚好到学校.则小宇家离学校的距离为( )
A.1800米 B.2000米 C.2800米 D.3200米
11、甲、乙两店以同样价格出售一种商品,并推出不同的优惠方:在甲店累计购物超过元后,超出元的部分打折;在乙店累计购物超过元后,超出元的部分打折,则顾客到两店购物花费一样时为( )
A.累计购物不超过元 B.累计购物超过元不超过元
C.累计购物超过元 D.累计购物不超过元或刚好为元
12、如图,长方形中有6个形状、大小相同的小长方形,且,则图中阴影部分的面积为( )
A.216 B.144 C.192 D.96
二、填空题
13、如果2(x+3)与3(1-x)互为相反数,那么x的值为______
14、如图,在数轴上,点A、B分别表示a、b,且,若,则点A表示的数为_____
15、有人要去某关口,路程378里,第一天健步行走,从第二天起, 由于脚痛,每天走的路程都为前一天的一半,一共走了六天才到达目的地,则此人第三天走的路程为_______里
16、端午节买粽子,每个肉粽比素粽多1元,购买10个肉粽和5个素粽共用去70元,设每个肉粽x元,则可列方程为__________
17、已知9人用14天完成了一件工作的,且每个人的工作效率相同,而剩下的工作要在4天完成,
则需增加的人数是__________
18、某车间有26名工人,每人每天可以生产800个螺钉或1000个螺母,一个螺钉需要配两个螺母,为使每天生产的螺钉和螺母刚好配套,所有工人全部参与生产,则生产螺钉的工人有______人.
19、北流市某风景区的门票价格在2019年国庆期间有如下优惠:购票人数为1~50人时,每人票价格为50元;购票人数为51~100人时,每人门票价格45元;购票人数为100人以上时,每人门票价格为40元.某初中初一有两班共103人去该风景区,如果两班都以班为单位分别购票,一共需付 4860元,则两班人数分别为( )
A.56,47 B.57,48 C.58,45 D.59,44
20、元旦期间某商店进行促销活动,活动方式有如下两种:
方式一:每满200元减50元;
方式二:若标价不超过400元时,打8折;
若标价超过400元,则不超过400元的部分打8折,超出400元的部分打6折.
某一商品的标价为元,当时,x取值为_________________时,两种方式的售价相同.
三、解答题
21、某车间共有75名工人生产A、B两种工件,已知一名工人每天可生产A种工件15件或B种工件20件,但要安装一台机械时,同时需A种工件1件,B种工件2件,才能配套,问车间如何分配工人生产,才能保证连续安装机械时,两种工件恰好配套?
22、甲、乙两人在一条长400 m的环形跑道上跑步,甲的速度是360 m/min,乙的速度是240 m/min.
(1)两人同时同地同向跑,问:第一次相遇时,两人一共跑了几圈?
(2)两人同时同地反向跑,问:几秒后两人第一次相遇?
23、有两种消费券:券,满60元减20元;券,满90元减30元,即一次购物大于等于60元、90元,付款时分别减20元、30元.小敏有一张券,小聪有一张券,他们都购买了一件标价相同的商品,各自付款,若能用券时用券,这样两人共付款150元,求所购商品的标价是多少元?
24、某超市计划购进甲、乙两种商品共件,这两种商品的进价、售价如下表:
进价(元/件) 售价(元/件)
甲
乙
(1)超市如何进货,进货款恰好为元?
(2)为确保乙商品畅销,在(1)的条件下,商家决定对乙商品进行打折出售,且全部售完后,乙商品的利润率为,请问乙商品需打几折?
25、用80m的篱笆围成一个长方形场地.
(1)如果宽是长的,求这个长方形的长和宽;
(2)如果长比宽多6m,求这个长方形的面积;
(3)如果一边靠墙,墙长为32m,长比宽多11m(长边与墙平行),这样设计是否可行?请说明理由.
26、如图,小刘和小周分别站在正方形的对角A C两点处,小刘以的速度走向点D处,途中位置记为P;小周以的速度走向点B处,途中位置记为Q.已知正方形的边长为,E在AB上, ,记三角形AEP的面积为,三角形BEQ的面积为.假设两人同时出发,运动的时间为.
(1)用含t的代数式表示下列线段的长度:
________;________;________;________;
(2)当t为何值时,
(3)他们出发多少秒时,
27、某种海产品,若直接销售,每吨可获利润1200元;若粗加工后销售,每吨可获利润5000元;若精加工后销售,每吨可获利润7500元.某公司现有这种海产品140吨,该公司的生产能力是:如果进行粗加工,每天可加工16吨;如果进行精加工,每天可加工6吨,但两种加工方式不能同时进行,受各种条件限制,公司必须在15天内将这批海产品全部销售或加工完毕,为此该公司设计了三种方案:
方案一:全部进行粗加工;
方案二:尽可能多地进行精加工,没有来得及进行精加工的直接销售;
方案三:将一部分进行精加工,其余的进行粗加工,并恰好15天完成.
你认为选择哪种方案可获利润最多,为什么?最多可获利润多少元?
28、如图,甲、乙两个圆柱形玻璃容器各盛有一定量的液体,甲、乙容器的内底面半径分别为和,现将一个半径为的圆柱形玻璃棒(足够长)垂直触底插入甲容器,此时甲、乙两个容器的液面高均为(如图①),再将此玻璃棒垂直触底插入乙容器(液体损耗忽略不计),此时乙容器的液面比甲容器的液面高(如图②).
(1)求甲、乙两个容器的内底面面积.
(2)如图①,分别求出甲、乙容器内液体的体积(用含h的代数式表示).
(3)求h的值.
3.2一元一次方程的应用【课后综合练】
-2021-2022学年七年级数学上册(沪科版)(解析)
一、选择题
1、王芳和李丽同时采摘樱桃,王芳平均每小时采摘,李丽平均每小时采摘.采摘结束后,王芳从她采摘的樱桃中取出给了李丽,这时两人的樱桃一样多.她们采摘用了多长时间?设她们采摘所用时间为小时,下列方程正确的是( )
A. B.
C. D.
【答案】D
【分析】
根据王芳从她采摘的樱桃中取出0.25kg给了李丽,这时两人的樱桃一样多得出方程求出答案.
【详解】
设她们采摘用了小时,
根据题意可得:,
故选:D.
2、某商品的进价是1528元,按商品标价的八折出售时,利润是12%,如果设商品的标价为x元,那么可列出正确的方程是( )
A. B.
C. D.
【答案】C
【分析】
根据题意找出题中存在的等量关系:售价=进价+利润,分别用式子表示等式的各部分,即可列出方程.
【详解】
解:设商品的标价为x元,则售价为0.8x元,
由题意,得0.8x=1528+1528×12%,
即0.8x=1528×(1+12%).
故选:C.
3、一项工程甲单独做要40天完成,乙单独做需要50天完成.如果甲先单独做4天,然后两人合作天完成这项工程,则可列的方程正确的是( )
A. B.
C. D.
【答案】D
【分析】
由题意一项工程甲单独做要40天完成,乙单独做需要50天完成,可以得出甲每天做整个工程的,乙每天做整个工程的,根据文字表述得到题目中的相等关系是:甲完成的部分+两人共同完成的部分=1.
【详解】
解:设整个工程为1,根据关系式甲完成的部分+两人共同完成的部分=1列出方程式为:
,
故选:D.
4、某校教师举行茶话会.若每桌坐10人,则空出一张桌子;若每桌坐8人,还有6人不能就坐.设该校准备的桌子数为x,则可列方程为( )
A.10(x﹣1)=8x﹣6 B.10(x﹣1)=8x+6
C.10(x+1)=8x﹣6 D.10(x+1)=8x+6
【答案】B
【分析】
设该校准备的桌子数为x,根据“若每桌坐10人,则空出一张桌子;若每桌坐8人,还有6人不能就坐”,即可得出关于x的一元一次方程,此题得解.
【详解】
解:设该校准备的桌子数为x,
依题意得:10(x-1)=8x+6.
故选:B.
5、一个两位数的十位数字与个位数字的和是9.如果把这个两位数加上63,那么恰好成为原两位数的个位数字与十位数字对调后组成的两位数,则原两位数是( ).
A.18 B.27 C.36 D.45
【答案】A
【分析】
据题意逐一检查对照,完全满足题目条件的就是正确选项.
【详解】
对于四个选项,1+8=9,2+7=9,3+6=9,4+5=9它们均满足十位数字与个位数字的和是9;
对于A:18+63=81,其结果恰好成为原两位数的个位数字与十位数字对调后组成的两位数;
对于B、C、D:27+63=90,36+63=99,45+63=108,其结果均不是原两位数的个位数字与十位数字对调后组成的两位数.只有A选项完全完全满足题目条件.
故选:A.
6、已知某商店有两件进价不同的运动衫都卖了160元,其中一件盈利60%,另一件亏损20%,在这次买卖 中这家商店( )
A.不盈不亏 B.盈利20元 C.盈利10元 D.亏损20元
【答案】B
【分析】
设分别设两件运动衫的进价分别是a元,b元,根据售价=成本±利润,列方程求得两件运动衫的进价,再计算亏盈.
【详解】
解:设盈利60%的运动衫的进价是a元,亏本20%的运动衫的进价是b元.则有
(1)a(1+60%)=160,a=100;
(2)b(1-20%)=160,b=200.
总售价是160+160=320(元),总进价是100+200=300(元),
320-300=20(元),
所以这次买卖中商家赚了20元.
故选:B.
7、一份数学试卷,有25道选择题,做对一道题得4分,做错一道题倒扣1分,某同学做了全部试题,得了80分,他共做对了( )
A.18道 B.19道 C.20道 D.21道
【答案】D
【分析】
设他共做对了x道题,根据题意列出方程并求解即可.
【详解】
设他共做对了x道题,根据题意得,
,
解得,
∴他共做对了21道题.
故选:D.
8、-2021年中考数学一轮复习讲练测(北京))如图是某月的月历,用形如“十”字型框任意框出5个数.对于任何一个月的月历,这5个数的和不可能是( )
A.125 B.115 C.110 D.40
【答案】A
【分析】设这5个数中间的一个为,则上面的数是,下面的数是,前面一个是,后面一个是,从而可得五个数的和为:,再列方程求解 并检验在表格中的位置,从而可得答案.
【详解】解:设这5个数中间的一个为,则上面的数是,下面的数是,前面一个是,后面一个是,
这五个数的和为:.
、如果,那么,而“十”字型框中25在第一列,不能是中间的数,即这5个数的和不可能是125,故本选项符合题意;
、如果,那么,23可以是“十”字型框中间的数,即这5个数的和可能是115,故本选项不符合题意;
、如果,那么,22可以是“十”字型框中间的数,即这5个数的和可能是110,故本选项不符合题意;
、如果,那么,8可以是“十”字型框中间的数,即这5个数的和可能是40,故本选项不符合题意;
故选:.
9、《孙子算经》中有这样一道题,原文如下:今有百鹿入城,家取一鹿,不尽,又三家共一鹿,适尽.问:城中家几何?大意为:今有100头鹿进城,每家取一头鹿,没有取完,剩下的每3家共取一头,恰好取完.问城中有多少户人家?( )
A.55户 B.65户 C.75户 D.85户
【答案】C
【分析】
设城中有户人家,由题意列一元一次方程,解一元一次方程即可解题.
【详解】
解:设城中有户人家,根据题意得,
解得
故选:C.
10、一天早上,小宇从家出发去上学.小宇在离家800米时,突然想起班级今天要进行建党100周年合唱彩排,表演的衣服忘了,于是小宇立即打电话通知妈妈送来,自己则一直保持原来的速度继续赶往学校,妈妈接到电话后,马上拿起衣服以180米/分的速度沿相同的路线追赶小宇,10分钟后追上了小宇,把衣服给小宇后又立即以原速原路返回,小宇拿到衣服后继续原速赶往学校(打接电话、拿取衣服等时间都忽略不计).当小宇妈妈回到家中时,恰好小宇也刚好到学校.则小宇家离学校的距离为( )
A.1800米 B.2000米 C.2800米 D.3200米
【答案】C
【分析】
设小宇的速度为米/分,根据“小宇拿到衣服后所走的路程=妈妈10分钟所走的路程-800”列方程求解即可.
【详解】
解:设小宇的速度为米/分,
根据题意得:,
解得:,
则小宇家离学校的距离为(米),
故选:C.
11、甲、乙两店以同样价格出售一种商品,并推出不同的优惠方:在甲店累计购物超过元后,超出元的部分打折;在乙店累计购物超过元后,超出元的部分打折,则顾客到两店购物花费一样时为( )
A.累计购物不超过元 B.累计购物超过元不超过元
C.累计购物超过元 D.累计购物不超过元或刚好为元
【答案】D
【分析】设顾客累计购物x元时,两店花费一样多,分x>100及x≤50两种情况考虑,当x≤50时,显然两店花费一样多;当x>100时,根据优惠方案列出关于x的一元一次方程,解之即可得出结论.
【详解】解:设顾客累计购物x元时,两店花费一样多,
当x>100时,有100+(x100)=50+(x50), 解得:x=150;
当x≤50时,两店花费均为x元.
答:累计购物不超过50元或刚好为150元时,两店花费一样多.
故选:D.
12、如图,长方形中有6个形状、大小相同的小长方形,且,则图中阴影部分的面积为( )
A.216 B.144 C.192 D.96
【答案】C
【分析】设每小长方形的宽为x,则每小长方形的长为x+6,根据一个小长方形的宽+2个小长方形的长=CD,列出方程,求出x的值,再根据长方形的面积公式用最大的长方形减去6个最小的小长方形的面积,得出阴影部分的面积.
【详解】解:设每小长方形的宽为x,则每小长方形的长为x+6,根据题意得:
2(x+6)+x=24,解得:x=4,
则每小长方形的长为4+6=10,
则AD=4+4+10=18,
阴影部分的面积为18×24-4×10×6=192;
故选:C.
二、填空题
13、如果2(x+3)与3(1-x)互为相反数,那么x的值为______
【答案】9
【分析】
由于2(x+3)与3(1 x)互为相反数,那么2(x+3)+3(1 x)=0,解此方程即可解决问题.
【详解】
∵2(x+3)与3(1-x)互为相反数,
∴2(x+3)+3(1-x)=0,
解得x=9,
14、如图,在数轴上,点A、B分别表示a、b,且,若,则点A表示的数为_____
【答案】-3
【分析】
由AB的长度结合A、B表示的数互为相反数,即可得出A,B表示的数
【详解】
解:∵, ∴,两点对应的数互为相反数,
∴可设表示的数为,则表示的数为,
∵, ∴,解得:,
∴点表示的数为-3,
15、有人要去某关口,路程378里,第一天健步行走,从第二天起, 由于脚痛,每天走的路程都为前一天的一半,一共走了六天才到达目的地,则此人第三天走的路程为_______里
【答案】48
【分析】设此人第三天走的路程为x里,则其它五天走的路程分别为4x里,2x里,x里,x里,x里,根据六天共走了378里,即可得出关于x的一元一次方程,解之即可得出结论.
【详解】
解:设此人第三天走的路程为x里,则其它五天走的路程分别为4x里,2x里,x里,x里,x里,
依题意,得:4x+2x+x+x+x+x=378,
解得:x=48.
16、端午节买粽子,每个肉粽比素粽多1元,购买10个肉粽和5个素粽共用去70元,设每个肉粽x元,则可列方程为__________
【答案】
【分析】
根据题意表示出肉粽和素粽的单价,再列出方程即可.
【详解】
设每个肉粽x元,则每个素粽的单价为(x-1)元,
由题意:,
17、已知9人用14天完成了一件工作的,且每个人的工作效率相同,而剩下的工作要在4天完成,
则需增加的人数是__________
【答案】12
【分析】
设剩下的工作要在4天内完成,需要增加的人数是x人,根据工程问题的数量关系建立方程求出其解即可.
【详解】
设剩下的工作要在4天内完成,需要增加的人数是x人,由题意,得
( ÷9÷14)×4×(9+x)=1 ,
解得:x=12.
18、某车间有26名工人,每人每天可以生产800个螺钉或1000个螺母,一个螺钉需要配两个螺母,为使每天生产的螺钉和螺母刚好配套,所有工人全部参与生产,则生产螺钉的工人有______人.
【答案】10.
【分析】
设安排x名工人生产螺钉,则安排(26﹣x)名工人生产螺母,根据生产的螺母总数是生产螺钉总数的2倍,即可得出关于x的一元一次方程,解之即可得出结论.
【详解】
解:设安排x名工人生产螺钉,则安排(26﹣x)名工人生产螺母,
依题意,得:2×800x=1000(26﹣x),
解得:x=10.
故答案为:10.
19、北流市某风景区的门票价格在2019年国庆期间有如下优惠:购票人数为1~50人时,每人票价格为50元;购票人数为51~100人时,每人门票价格45元;购票人数为100人以上时,每人门票价格为40元.某初中初一有两班共103人去该风景区,如果两班都以班为单位分别购票,一共需付 4860元,则两班人数分别为( )
A.56,47 B.57,48 C.58,45 D.59,44
【答案】C
【分析】
要考虑有两种情况:①若(1)班人数为1~50人,(2)班的人数为51~100人时;②若(1)班人数为1~50人,(2)班的人数为100人以上时;分别计算,不符合的情况舍去就可以了.
【详解】∵103×45=4635<4860,∴一个班的人数不多于50人,另一个班的人数多于50人,
①若(1)班人数为1~50人,(2)班的人数为51~100人时,
设(1)班有x人,(2)班有(103-x)人,
则由题意,得50x+45(103-x)=4860,
解得x=45,
∴103-x=58人,经检验符合题意;
②若(1)班人数为1~50人,(2)班的人数为100人以上时,
设(1)班有x人,(2)班有(103-x)人,
则由题意,得50x+40(103-x)=4860,
解得x=74,
∴103-x=29人,经检验不符合题意,舍去;
∴一个班有45人,另一个班有58人.
故选C.
20、元旦期间某商店进行促销活动,活动方式有如下两种:
方式一:每满200元减50元;
方式二:若标价不超过400元时,打8折;
若标价超过400元,则不超过400元的部分打8折,超出400元的部分打6折.
某一商品的标价为元,当时,x取值为_________________时,两种方式的售价相同.
【答案】250或450.
【分析】
根据题意,分两种情况讨论,当或当时,列出方程进行解得即可.
【详解】
解:当时,, 解得;
当时,
, , 解得,
当时,取值为250或450时,两种方式的售价相同,
故答案为:250或450.
三、解答题
21、某车间共有75名工人生产A、B两种工件,已知一名工人每天可生产A种工件15件或B种工件20件,但要安装一台机械时,同时需A种工件1件,B种工件2件,才能配套,问车间如何分配工人生产,才能保证连续安装机械时,两种工件恰好配套?
答案:该车间分配30名工人生产A种工件,45名工人生产B种工件才能保证连续安装机械时两种工件恰好配套.
解答:设该车间分配x名工人生产A种工件,(75-x)名工人生产B种工件才能保证连续安装机械时两种工件恰好配套,
根据题意得2×15x=20(75-x),
解得:x=30,
则75-x=45,
答:该车间分配30名工人生产A种工件,45名工人生产B种工件才能保证连续安装机械时两种工件恰好配套.
22、甲、乙两人在一条长400 m的环形跑道上跑步,甲的速度是360 m/min,乙的速度是240 m/min.
(1)两人同时同地同向跑,问:第一次相遇时,两人一共跑了几圈?
(2)两人同时同地反向跑,问:几秒后两人第一次相遇?
解:(1)设x分后两人第一次相遇,由题意,得360x-240x=400.
解得x=, ==5(圈).
答:两人一共跑了5圈.
(2)设x分钟后两人第一次相遇.
由题意,得360x+240x=400,
解得x=, min=40 s.
答:40 s后两人第一次相遇.
23、有两种消费券:券,满60元减20元;券,满90元减30元,即一次购物大于等于60元、90元,付款时分别减20元、30元.小敏有一张券,小聪有一张券,他们都购买了一件标价相同的商品,各自付款,若能用券时用券,这样两人共付款150元,求所购商品的标价是多少元?
【答案】100或85元
【分析】设商品的标价为元,依据题意对进行讨论,分别列方程组求解即可.
【详解】解:设所购商品的标价是元,由题意可知,;依题意得
①当时,,解得;
②当元,,解得.
故所购商品的标价是或元.
24、某超市计划购进甲、乙两种商品共件,这两种商品的进价、售价如下表:
进价(元/件) 售价(元/件)
甲
乙
(1)超市如何进货,进货款恰好为元?
(2)为确保乙商品畅销,在(1)的条件下,商家决定对乙商品进行打折出售,且全部售完后,乙商品的利润率为,请问乙商品需打几折?
【答案】(1)购进甲商品件,购进乙商品件进货款恰好为元;(2)乙商品需打折.
【分析】
(1)设商场购进甲商品件,则购进乙商品件,然后根据题意及表格可列方程求解;
(2)设乙商品需打折,根据题意可直接列方程求解.
【详解】
解:(1)设商场购进甲商品件,则购进乙商品件,
由题意,得
解得:
购进乙商品(件).
答:购进甲商品件,购进乙商品件进货款恰好为元.
(2)设乙商品需打折,由题意得:
,
解得.
答:乙商品需打折.
25、用80m的篱笆围成一个长方形场地.
(1)如果宽是长的,求这个长方形的长和宽;
(2)如果长比宽多6m,求这个长方形的面积;
(3)如果一边靠墙,墙长为32m,长比宽多11m(长边与墙平行),这样设计是否可行?请说明理由.
【答案】(1)这个长方形的长是25m,宽是15m;
(2)这个长方形的面积为391m ;
(3)这样设计不可行,详见解析.
【解析】
【分析】
(1设长方形的长为xm,则宽为xm,列出方程求解即可解答;
(2)设长方形的长为xm,则宽为(x-6)m,列出方程求解即可解答;
(3)设长方形的长为xm,则宽为(x-11)m,列出方程求出x的值,然后将x的值与墙的长度进行比较,即可分析设计是否可行.
【详解】
(1)设长方形的长为xm,则宽为xm,
则有:(x+x)×2=80,解得,x=25,
答:这个长方形的长是25m,宽是15m;
(2)设长方形的长为xm,则宽为(x-6)m,
则有:(x+x-6)×2=80,解得,x=23,
∴这个长方形的面积为:23×(23-6)=391(m ),
答:这个长方形的面积为391m ;
(3)设长方形的长为xm,则宽为(x-11)m,
则有:x+(x-11)×2=80,
解得,x=34,
∵长方形的长度大于墙的长度,不符合题意要求,∴设计是不可行的.
26、如图,小刘和小周分别站在正方形的对角A C两点处,小刘以的速度走向点D处,途中位置记为P;小周以的速度走向点B处,途中位置记为Q.已知正方形的边长为,E在AB上, ,记三角形AEP的面积为,三角形BEQ的面积为.假设两人同时出发,运动的时间为.
(1)用含t的代数式表示下列线段的长度:
________;________;________;________;
(2)当t为何值时,
(3)他们出发多少秒时,
【答案】(1),,,;(2);(3)
【分析】(1)由路程=速度×时间以及图形中相关线段间的和差关系填空;
(2)根据题意列出方程8 2t=3t,则易求t的值;
(3)利用三角形的面积公式和等量关系列出方程×2t×6=(8 6)×(8 3t),通过解方程易求t的值.
【详解】解:(1)∵小刘以的速度走向点D,∴,则,
∵小周以的速度走向点B处,∴,则,
故答案为:;;;;
(2)由题意,可得,
解得. 即当时,;
(3)设他们出发时,则小刘所走路程为,即;
小周所走路程为,则;
由题意得.
解得, 即他们出发时,.
27、某种海产品,若直接销售,每吨可获利润1200元;若粗加工后销售,每吨可获利润5000元;若精加工后销售,每吨可获利润7500元.某公司现有这种海产品140吨,该公司的生产能力是:如果进行粗加工,每天可加工16吨;如果进行精加工,每天可加工6吨,但两种加工方式不能同时进行,受各种条件限制,公司必须在15天内将这批海产品全部销售或加工完毕,为此该公司设计了三种方案:
方案一:全部进行粗加工;
方案二:尽可能多地进行精加工,没有来得及进行精加工的直接销售;
方案三:将一部分进行精加工,其余的进行粗加工,并恰好15天完成.
你认为选择哪种方案可获利润最多,为什么?最多可获利润多少元?
【答案】方案三可获利润最多,最多可获利润850000元.
【分析】方案一由于全部进行粗加工,而16×15>140,所以粗加工可以全部加工完,然后每吨可获利润5000元即可求出利润;方案二由于尽可能多地进行精加工,没有来得及进行精加工的直接销售,那么15天可精加工6×15=90吨,剩下的直接销售,再根据已知条件也可求出利润;方案三由于将一部分进行精加工,其余的进行粗加工,并恰好15天完成,那么设将x吨海产品进行精加工,则将(140-x)吨进行粗加工,根据恰好15天完成可以列出方程求出精加工和粗加工各自的吨数,然后利用已知条件求出利润.
【详解】
解:方案一:可获利润为:5000×140=700000(元);
方案二:15天可精加工6×15=90(吨),
说明还有50吨需要直接销售,
故可获利润:7500×90+1200×50=735000(元);
方案三:设将x吨海产品进行精加工,则将(140-x)吨进行粗加工,
由题意得:,
解得:x=60,
故可获利润7500×60+5000×80=850000(元),
∵850000>735000>700000,
所以选择方案三可获利润最多,最多可获利润850000元.
28、如图,甲、乙两个圆柱形玻璃容器各盛有一定量的液体,甲、乙容器的内底面半径分别为和,现将一个半径为的圆柱形玻璃棒(足够长)垂直触底插入甲容器,此时甲、乙两个容器的液面高均为(如图①),再将此玻璃棒垂直触底插入乙容器(液体损耗忽略不计),此时乙容器的液面比甲容器的液面高(如图②).
(1)求甲、乙两个容器的内底面面积.
(2)如图①,分别求出甲、乙容器内液体的体积(用含h的代数式表示).
(3)求h的值.
【答案】(1)36πcm2,16πcm2;(2)32πh(cm3),16πh(cm3);(3)
【分析】(1)由甲、乙容器的内底面半径分别为6cm和4cm,可得甲、乙两个容器的内底面面积;
(2)根据题意,即可得甲、乙容器内液体的体积;
(3)根据题意乙的液体体积不变,可列出方程即可求得h的值.
【详解】解:(1)由甲、乙容器的内底面半径分别为6cm和4cm,
所以甲、乙两个容器的内底面面积分别为:36πcm2,16πcm2.
答:甲、乙两个容器的内底面面积分别为:36πcm2,16πcm2.
(2)根据题意,得
甲容器内液体的体积为:36πh-4πh=32πh(cm3);
乙容器内液体的体积为:16πh(cm3);
(3)根据题意可知:
乙的液体体积不变,可得16πh=(16π-4π)(+3)
解得h=,
答:h的值为.
-2021-2022学年七年级数学上册(沪科版)
一、选择题
1、王芳和李丽同时采摘樱桃,王芳平均每小时采摘,李丽平均每小时采摘.采摘结束后,王芳从她采摘的樱桃中取出给了李丽,这时两人的樱桃一样多.她们采摘用了多长时间?设她们采摘所用时间为小时,下列方程正确的是( )
A. B.
C. D.
2、某商品的进价是1528元,按商品标价的八折出售时,利润是12%,如果设商品的标价为x元,那么可列出正确的方程是( )
A. B.
C. D.
3、一项工程甲单独做要40天完成,乙单独做需要50天完成.如果甲先单独做4天,然后两人合作天完成这项工程,则可列的方程正确的是( )
A. B. C. D.
4、某校教师举行茶话会.若每桌坐10人,则空出一张桌子;若每桌坐8人,还有6人不能就坐.设该校准备的桌子数为x,则可列方程为( )
A.10(x﹣1)=8x﹣6 B.10(x﹣1)=8x+6
C.10(x+1)=8x﹣6 D.10(x+1)=8x+6
5、一个两位数的十位数字与个位数字的和是9.如果把这个两位数加上63,那么恰好成为原两位数的个位数字与十位数字对调后组成的两位数,则原两位数是( ).
A.18 B.27 C.36 D.45
6、已知某商店有两件进价不同的运动衫都卖了160元,其中一件盈利60%,另一件亏损20%,在这次买卖 中这家商店( )
A.不盈不亏 B.盈利20元 C.盈利10元 D.亏损20元
7、一份数学试卷,有25道选择题,做对一道题得4分,做错一道题倒扣1分,某同学做了全部试题,得了80分,他共做对了( )
A.18道 B.19道 C.20道 D.21道
8、-2021年中考数学一轮复习讲练测(北京))如图是某月的月历,用形如“十”字型框任意框出5个数.对于任何一个月的月历,这5个数的和不可能是( )
A.125 B.115 C.110 D.40
9、《孙子算经》中有这样一道题,原文如下:今有百鹿入城,家取一鹿,不尽,又三家共一鹿,适尽.问:城中家几何?大意为:今有100头鹿进城,每家取一头鹿,没有取完,剩下的每3家共取一头,恰好取完.问城中有多少户人家?( )
A.55户 B.65户 C.75户 D.85户
10、一天早上,小宇从家出发去上学.小宇在离家800米时,突然想起班级今天要进行建党100周年合唱彩排,表演的衣服忘了,于是小宇立即打电话通知妈妈送来,自己则一直保持原来的速度继续赶往学校,妈妈接到电话后,马上拿起衣服以180米/分的速度沿相同的路线追赶小宇,10分钟后追上了小宇,把衣服给小宇后又立即以原速原路返回,小宇拿到衣服后继续原速赶往学校(打接电话、拿取衣服等时间都忽略不计).当小宇妈妈回到家中时,恰好小宇也刚好到学校.则小宇家离学校的距离为( )
A.1800米 B.2000米 C.2800米 D.3200米
11、甲、乙两店以同样价格出售一种商品,并推出不同的优惠方:在甲店累计购物超过元后,超出元的部分打折;在乙店累计购物超过元后,超出元的部分打折,则顾客到两店购物花费一样时为( )
A.累计购物不超过元 B.累计购物超过元不超过元
C.累计购物超过元 D.累计购物不超过元或刚好为元
12、如图,长方形中有6个形状、大小相同的小长方形,且,则图中阴影部分的面积为( )
A.216 B.144 C.192 D.96
二、填空题
13、如果2(x+3)与3(1-x)互为相反数,那么x的值为______
14、如图,在数轴上,点A、B分别表示a、b,且,若,则点A表示的数为_____
15、有人要去某关口,路程378里,第一天健步行走,从第二天起, 由于脚痛,每天走的路程都为前一天的一半,一共走了六天才到达目的地,则此人第三天走的路程为_______里
16、端午节买粽子,每个肉粽比素粽多1元,购买10个肉粽和5个素粽共用去70元,设每个肉粽x元,则可列方程为__________
17、已知9人用14天完成了一件工作的,且每个人的工作效率相同,而剩下的工作要在4天完成,
则需增加的人数是__________
18、某车间有26名工人,每人每天可以生产800个螺钉或1000个螺母,一个螺钉需要配两个螺母,为使每天生产的螺钉和螺母刚好配套,所有工人全部参与生产,则生产螺钉的工人有______人.
19、北流市某风景区的门票价格在2019年国庆期间有如下优惠:购票人数为1~50人时,每人票价格为50元;购票人数为51~100人时,每人门票价格45元;购票人数为100人以上时,每人门票价格为40元.某初中初一有两班共103人去该风景区,如果两班都以班为单位分别购票,一共需付 4860元,则两班人数分别为( )
A.56,47 B.57,48 C.58,45 D.59,44
20、元旦期间某商店进行促销活动,活动方式有如下两种:
方式一:每满200元减50元;
方式二:若标价不超过400元时,打8折;
若标价超过400元,则不超过400元的部分打8折,超出400元的部分打6折.
某一商品的标价为元,当时,x取值为_________________时,两种方式的售价相同.
三、解答题
21、某车间共有75名工人生产A、B两种工件,已知一名工人每天可生产A种工件15件或B种工件20件,但要安装一台机械时,同时需A种工件1件,B种工件2件,才能配套,问车间如何分配工人生产,才能保证连续安装机械时,两种工件恰好配套?
22、甲、乙两人在一条长400 m的环形跑道上跑步,甲的速度是360 m/min,乙的速度是240 m/min.
(1)两人同时同地同向跑,问:第一次相遇时,两人一共跑了几圈?
(2)两人同时同地反向跑,问:几秒后两人第一次相遇?
23、有两种消费券:券,满60元减20元;券,满90元减30元,即一次购物大于等于60元、90元,付款时分别减20元、30元.小敏有一张券,小聪有一张券,他们都购买了一件标价相同的商品,各自付款,若能用券时用券,这样两人共付款150元,求所购商品的标价是多少元?
24、某超市计划购进甲、乙两种商品共件,这两种商品的进价、售价如下表:
进价(元/件) 售价(元/件)
甲
乙
(1)超市如何进货,进货款恰好为元?
(2)为确保乙商品畅销,在(1)的条件下,商家决定对乙商品进行打折出售,且全部售完后,乙商品的利润率为,请问乙商品需打几折?
25、用80m的篱笆围成一个长方形场地.
(1)如果宽是长的,求这个长方形的长和宽;
(2)如果长比宽多6m,求这个长方形的面积;
(3)如果一边靠墙,墙长为32m,长比宽多11m(长边与墙平行),这样设计是否可行?请说明理由.
26、如图,小刘和小周分别站在正方形的对角A C两点处,小刘以的速度走向点D处,途中位置记为P;小周以的速度走向点B处,途中位置记为Q.已知正方形的边长为,E在AB上, ,记三角形AEP的面积为,三角形BEQ的面积为.假设两人同时出发,运动的时间为.
(1)用含t的代数式表示下列线段的长度:
________;________;________;________;
(2)当t为何值时,
(3)他们出发多少秒时,
27、某种海产品,若直接销售,每吨可获利润1200元;若粗加工后销售,每吨可获利润5000元;若精加工后销售,每吨可获利润7500元.某公司现有这种海产品140吨,该公司的生产能力是:如果进行粗加工,每天可加工16吨;如果进行精加工,每天可加工6吨,但两种加工方式不能同时进行,受各种条件限制,公司必须在15天内将这批海产品全部销售或加工完毕,为此该公司设计了三种方案:
方案一:全部进行粗加工;
方案二:尽可能多地进行精加工,没有来得及进行精加工的直接销售;
方案三:将一部分进行精加工,其余的进行粗加工,并恰好15天完成.
你认为选择哪种方案可获利润最多,为什么?最多可获利润多少元?
28、如图,甲、乙两个圆柱形玻璃容器各盛有一定量的液体,甲、乙容器的内底面半径分别为和,现将一个半径为的圆柱形玻璃棒(足够长)垂直触底插入甲容器,此时甲、乙两个容器的液面高均为(如图①),再将此玻璃棒垂直触底插入乙容器(液体损耗忽略不计),此时乙容器的液面比甲容器的液面高(如图②).
(1)求甲、乙两个容器的内底面面积.
(2)如图①,分别求出甲、乙容器内液体的体积(用含h的代数式表示).
(3)求h的值.
3.2一元一次方程的应用【课后综合练】
-2021-2022学年七年级数学上册(沪科版)(解析)
一、选择题
1、王芳和李丽同时采摘樱桃,王芳平均每小时采摘,李丽平均每小时采摘.采摘结束后,王芳从她采摘的樱桃中取出给了李丽,这时两人的樱桃一样多.她们采摘用了多长时间?设她们采摘所用时间为小时,下列方程正确的是( )
A. B.
C. D.
【答案】D
【分析】
根据王芳从她采摘的樱桃中取出0.25kg给了李丽,这时两人的樱桃一样多得出方程求出答案.
【详解】
设她们采摘用了小时,
根据题意可得:,
故选:D.
2、某商品的进价是1528元,按商品标价的八折出售时,利润是12%,如果设商品的标价为x元,那么可列出正确的方程是( )
A. B.
C. D.
【答案】C
【分析】
根据题意找出题中存在的等量关系:售价=进价+利润,分别用式子表示等式的各部分,即可列出方程.
【详解】
解:设商品的标价为x元,则售价为0.8x元,
由题意,得0.8x=1528+1528×12%,
即0.8x=1528×(1+12%).
故选:C.
3、一项工程甲单独做要40天完成,乙单独做需要50天完成.如果甲先单独做4天,然后两人合作天完成这项工程,则可列的方程正确的是( )
A. B.
C. D.
【答案】D
【分析】
由题意一项工程甲单独做要40天完成,乙单独做需要50天完成,可以得出甲每天做整个工程的,乙每天做整个工程的,根据文字表述得到题目中的相等关系是:甲完成的部分+两人共同完成的部分=1.
【详解】
解:设整个工程为1,根据关系式甲完成的部分+两人共同完成的部分=1列出方程式为:
,
故选:D.
4、某校教师举行茶话会.若每桌坐10人,则空出一张桌子;若每桌坐8人,还有6人不能就坐.设该校准备的桌子数为x,则可列方程为( )
A.10(x﹣1)=8x﹣6 B.10(x﹣1)=8x+6
C.10(x+1)=8x﹣6 D.10(x+1)=8x+6
【答案】B
【分析】
设该校准备的桌子数为x,根据“若每桌坐10人,则空出一张桌子;若每桌坐8人,还有6人不能就坐”,即可得出关于x的一元一次方程,此题得解.
【详解】
解:设该校准备的桌子数为x,
依题意得:10(x-1)=8x+6.
故选:B.
5、一个两位数的十位数字与个位数字的和是9.如果把这个两位数加上63,那么恰好成为原两位数的个位数字与十位数字对调后组成的两位数,则原两位数是( ).
A.18 B.27 C.36 D.45
【答案】A
【分析】
据题意逐一检查对照,完全满足题目条件的就是正确选项.
【详解】
对于四个选项,1+8=9,2+7=9,3+6=9,4+5=9它们均满足十位数字与个位数字的和是9;
对于A:18+63=81,其结果恰好成为原两位数的个位数字与十位数字对调后组成的两位数;
对于B、C、D:27+63=90,36+63=99,45+63=108,其结果均不是原两位数的个位数字与十位数字对调后组成的两位数.只有A选项完全完全满足题目条件.
故选:A.
6、已知某商店有两件进价不同的运动衫都卖了160元,其中一件盈利60%,另一件亏损20%,在这次买卖 中这家商店( )
A.不盈不亏 B.盈利20元 C.盈利10元 D.亏损20元
【答案】B
【分析】
设分别设两件运动衫的进价分别是a元,b元,根据售价=成本±利润,列方程求得两件运动衫的进价,再计算亏盈.
【详解】
解:设盈利60%的运动衫的进价是a元,亏本20%的运动衫的进价是b元.则有
(1)a(1+60%)=160,a=100;
(2)b(1-20%)=160,b=200.
总售价是160+160=320(元),总进价是100+200=300(元),
320-300=20(元),
所以这次买卖中商家赚了20元.
故选:B.
7、一份数学试卷,有25道选择题,做对一道题得4分,做错一道题倒扣1分,某同学做了全部试题,得了80分,他共做对了( )
A.18道 B.19道 C.20道 D.21道
【答案】D
【分析】
设他共做对了x道题,根据题意列出方程并求解即可.
【详解】
设他共做对了x道题,根据题意得,
,
解得,
∴他共做对了21道题.
故选:D.
8、-2021年中考数学一轮复习讲练测(北京))如图是某月的月历,用形如“十”字型框任意框出5个数.对于任何一个月的月历,这5个数的和不可能是( )
A.125 B.115 C.110 D.40
【答案】A
【分析】设这5个数中间的一个为,则上面的数是,下面的数是,前面一个是,后面一个是,从而可得五个数的和为:,再列方程求解 并检验在表格中的位置,从而可得答案.
【详解】解:设这5个数中间的一个为,则上面的数是,下面的数是,前面一个是,后面一个是,
这五个数的和为:.
、如果,那么,而“十”字型框中25在第一列,不能是中间的数,即这5个数的和不可能是125,故本选项符合题意;
、如果,那么,23可以是“十”字型框中间的数,即这5个数的和可能是115,故本选项不符合题意;
、如果,那么,22可以是“十”字型框中间的数,即这5个数的和可能是110,故本选项不符合题意;
、如果,那么,8可以是“十”字型框中间的数,即这5个数的和可能是40,故本选项不符合题意;
故选:.
9、《孙子算经》中有这样一道题,原文如下:今有百鹿入城,家取一鹿,不尽,又三家共一鹿,适尽.问:城中家几何?大意为:今有100头鹿进城,每家取一头鹿,没有取完,剩下的每3家共取一头,恰好取完.问城中有多少户人家?( )
A.55户 B.65户 C.75户 D.85户
【答案】C
【分析】
设城中有户人家,由题意列一元一次方程,解一元一次方程即可解题.
【详解】
解:设城中有户人家,根据题意得,
解得
故选:C.
10、一天早上,小宇从家出发去上学.小宇在离家800米时,突然想起班级今天要进行建党100周年合唱彩排,表演的衣服忘了,于是小宇立即打电话通知妈妈送来,自己则一直保持原来的速度继续赶往学校,妈妈接到电话后,马上拿起衣服以180米/分的速度沿相同的路线追赶小宇,10分钟后追上了小宇,把衣服给小宇后又立即以原速原路返回,小宇拿到衣服后继续原速赶往学校(打接电话、拿取衣服等时间都忽略不计).当小宇妈妈回到家中时,恰好小宇也刚好到学校.则小宇家离学校的距离为( )
A.1800米 B.2000米 C.2800米 D.3200米
【答案】C
【分析】
设小宇的速度为米/分,根据“小宇拿到衣服后所走的路程=妈妈10分钟所走的路程-800”列方程求解即可.
【详解】
解:设小宇的速度为米/分,
根据题意得:,
解得:,
则小宇家离学校的距离为(米),
故选:C.
11、甲、乙两店以同样价格出售一种商品,并推出不同的优惠方:在甲店累计购物超过元后,超出元的部分打折;在乙店累计购物超过元后,超出元的部分打折,则顾客到两店购物花费一样时为( )
A.累计购物不超过元 B.累计购物超过元不超过元
C.累计购物超过元 D.累计购物不超过元或刚好为元
【答案】D
【分析】设顾客累计购物x元时,两店花费一样多,分x>100及x≤50两种情况考虑,当x≤50时,显然两店花费一样多;当x>100时,根据优惠方案列出关于x的一元一次方程,解之即可得出结论.
【详解】解:设顾客累计购物x元时,两店花费一样多,
当x>100时,有100+(x100)=50+(x50), 解得:x=150;
当x≤50时,两店花费均为x元.
答:累计购物不超过50元或刚好为150元时,两店花费一样多.
故选:D.
12、如图,长方形中有6个形状、大小相同的小长方形,且,则图中阴影部分的面积为( )
A.216 B.144 C.192 D.96
【答案】C
【分析】设每小长方形的宽为x,则每小长方形的长为x+6,根据一个小长方形的宽+2个小长方形的长=CD,列出方程,求出x的值,再根据长方形的面积公式用最大的长方形减去6个最小的小长方形的面积,得出阴影部分的面积.
【详解】解:设每小长方形的宽为x,则每小长方形的长为x+6,根据题意得:
2(x+6)+x=24,解得:x=4,
则每小长方形的长为4+6=10,
则AD=4+4+10=18,
阴影部分的面积为18×24-4×10×6=192;
故选:C.
二、填空题
13、如果2(x+3)与3(1-x)互为相反数,那么x的值为______
【答案】9
【分析】
由于2(x+3)与3(1 x)互为相反数,那么2(x+3)+3(1 x)=0,解此方程即可解决问题.
【详解】
∵2(x+3)与3(1-x)互为相反数,
∴2(x+3)+3(1-x)=0,
解得x=9,
14、如图,在数轴上,点A、B分别表示a、b,且,若,则点A表示的数为_____
【答案】-3
【分析】
由AB的长度结合A、B表示的数互为相反数,即可得出A,B表示的数
【详解】
解:∵, ∴,两点对应的数互为相反数,
∴可设表示的数为,则表示的数为,
∵, ∴,解得:,
∴点表示的数为-3,
15、有人要去某关口,路程378里,第一天健步行走,从第二天起, 由于脚痛,每天走的路程都为前一天的一半,一共走了六天才到达目的地,则此人第三天走的路程为_______里
【答案】48
【分析】设此人第三天走的路程为x里,则其它五天走的路程分别为4x里,2x里,x里,x里,x里,根据六天共走了378里,即可得出关于x的一元一次方程,解之即可得出结论.
【详解】
解:设此人第三天走的路程为x里,则其它五天走的路程分别为4x里,2x里,x里,x里,x里,
依题意,得:4x+2x+x+x+x+x=378,
解得:x=48.
16、端午节买粽子,每个肉粽比素粽多1元,购买10个肉粽和5个素粽共用去70元,设每个肉粽x元,则可列方程为__________
【答案】
【分析】
根据题意表示出肉粽和素粽的单价,再列出方程即可.
【详解】
设每个肉粽x元,则每个素粽的单价为(x-1)元,
由题意:,
17、已知9人用14天完成了一件工作的,且每个人的工作效率相同,而剩下的工作要在4天完成,
则需增加的人数是__________
【答案】12
【分析】
设剩下的工作要在4天内完成,需要增加的人数是x人,根据工程问题的数量关系建立方程求出其解即可.
【详解】
设剩下的工作要在4天内完成,需要增加的人数是x人,由题意,得
( ÷9÷14)×4×(9+x)=1 ,
解得:x=12.
18、某车间有26名工人,每人每天可以生产800个螺钉或1000个螺母,一个螺钉需要配两个螺母,为使每天生产的螺钉和螺母刚好配套,所有工人全部参与生产,则生产螺钉的工人有______人.
【答案】10.
【分析】
设安排x名工人生产螺钉,则安排(26﹣x)名工人生产螺母,根据生产的螺母总数是生产螺钉总数的2倍,即可得出关于x的一元一次方程,解之即可得出结论.
【详解】
解:设安排x名工人生产螺钉,则安排(26﹣x)名工人生产螺母,
依题意,得:2×800x=1000(26﹣x),
解得:x=10.
故答案为:10.
19、北流市某风景区的门票价格在2019年国庆期间有如下优惠:购票人数为1~50人时,每人票价格为50元;购票人数为51~100人时,每人门票价格45元;购票人数为100人以上时,每人门票价格为40元.某初中初一有两班共103人去该风景区,如果两班都以班为单位分别购票,一共需付 4860元,则两班人数分别为( )
A.56,47 B.57,48 C.58,45 D.59,44
【答案】C
【分析】
要考虑有两种情况:①若(1)班人数为1~50人,(2)班的人数为51~100人时;②若(1)班人数为1~50人,(2)班的人数为100人以上时;分别计算,不符合的情况舍去就可以了.
【详解】∵103×45=4635<4860,∴一个班的人数不多于50人,另一个班的人数多于50人,
①若(1)班人数为1~50人,(2)班的人数为51~100人时,
设(1)班有x人,(2)班有(103-x)人,
则由题意,得50x+45(103-x)=4860,
解得x=45,
∴103-x=58人,经检验符合题意;
②若(1)班人数为1~50人,(2)班的人数为100人以上时,
设(1)班有x人,(2)班有(103-x)人,
则由题意,得50x+40(103-x)=4860,
解得x=74,
∴103-x=29人,经检验不符合题意,舍去;
∴一个班有45人,另一个班有58人.
故选C.
20、元旦期间某商店进行促销活动,活动方式有如下两种:
方式一:每满200元减50元;
方式二:若标价不超过400元时,打8折;
若标价超过400元,则不超过400元的部分打8折,超出400元的部分打6折.
某一商品的标价为元,当时,x取值为_________________时,两种方式的售价相同.
【答案】250或450.
【分析】
根据题意,分两种情况讨论,当或当时,列出方程进行解得即可.
【详解】
解:当时,, 解得;
当时,
, , 解得,
当时,取值为250或450时,两种方式的售价相同,
故答案为:250或450.
三、解答题
21、某车间共有75名工人生产A、B两种工件,已知一名工人每天可生产A种工件15件或B种工件20件,但要安装一台机械时,同时需A种工件1件,B种工件2件,才能配套,问车间如何分配工人生产,才能保证连续安装机械时,两种工件恰好配套?
答案:该车间分配30名工人生产A种工件,45名工人生产B种工件才能保证连续安装机械时两种工件恰好配套.
解答:设该车间分配x名工人生产A种工件,(75-x)名工人生产B种工件才能保证连续安装机械时两种工件恰好配套,
根据题意得2×15x=20(75-x),
解得:x=30,
则75-x=45,
答:该车间分配30名工人生产A种工件,45名工人生产B种工件才能保证连续安装机械时两种工件恰好配套.
22、甲、乙两人在一条长400 m的环形跑道上跑步,甲的速度是360 m/min,乙的速度是240 m/min.
(1)两人同时同地同向跑,问:第一次相遇时,两人一共跑了几圈?
(2)两人同时同地反向跑,问:几秒后两人第一次相遇?
解:(1)设x分后两人第一次相遇,由题意,得360x-240x=400.
解得x=, ==5(圈).
答:两人一共跑了5圈.
(2)设x分钟后两人第一次相遇.
由题意,得360x+240x=400,
解得x=, min=40 s.
答:40 s后两人第一次相遇.
23、有两种消费券:券,满60元减20元;券,满90元减30元,即一次购物大于等于60元、90元,付款时分别减20元、30元.小敏有一张券,小聪有一张券,他们都购买了一件标价相同的商品,各自付款,若能用券时用券,这样两人共付款150元,求所购商品的标价是多少元?
【答案】100或85元
【分析】设商品的标价为元,依据题意对进行讨论,分别列方程组求解即可.
【详解】解:设所购商品的标价是元,由题意可知,;依题意得
①当时,,解得;
②当元,,解得.
故所购商品的标价是或元.
24、某超市计划购进甲、乙两种商品共件,这两种商品的进价、售价如下表:
进价(元/件) 售价(元/件)
甲
乙
(1)超市如何进货,进货款恰好为元?
(2)为确保乙商品畅销,在(1)的条件下,商家决定对乙商品进行打折出售,且全部售完后,乙商品的利润率为,请问乙商品需打几折?
【答案】(1)购进甲商品件,购进乙商品件进货款恰好为元;(2)乙商品需打折.
【分析】
(1)设商场购进甲商品件,则购进乙商品件,然后根据题意及表格可列方程求解;
(2)设乙商品需打折,根据题意可直接列方程求解.
【详解】
解:(1)设商场购进甲商品件,则购进乙商品件,
由题意,得
解得:
购进乙商品(件).
答:购进甲商品件,购进乙商品件进货款恰好为元.
(2)设乙商品需打折,由题意得:
,
解得.
答:乙商品需打折.
25、用80m的篱笆围成一个长方形场地.
(1)如果宽是长的,求这个长方形的长和宽;
(2)如果长比宽多6m,求这个长方形的面积;
(3)如果一边靠墙,墙长为32m,长比宽多11m(长边与墙平行),这样设计是否可行?请说明理由.
【答案】(1)这个长方形的长是25m,宽是15m;
(2)这个长方形的面积为391m ;
(3)这样设计不可行,详见解析.
【解析】
【分析】
(1设长方形的长为xm,则宽为xm,列出方程求解即可解答;
(2)设长方形的长为xm,则宽为(x-6)m,列出方程求解即可解答;
(3)设长方形的长为xm,则宽为(x-11)m,列出方程求出x的值,然后将x的值与墙的长度进行比较,即可分析设计是否可行.
【详解】
(1)设长方形的长为xm,则宽为xm,
则有:(x+x)×2=80,解得,x=25,
答:这个长方形的长是25m,宽是15m;
(2)设长方形的长为xm,则宽为(x-6)m,
则有:(x+x-6)×2=80,解得,x=23,
∴这个长方形的面积为:23×(23-6)=391(m ),
答:这个长方形的面积为391m ;
(3)设长方形的长为xm,则宽为(x-11)m,
则有:x+(x-11)×2=80,
解得,x=34,
∵长方形的长度大于墙的长度,不符合题意要求,∴设计是不可行的.
26、如图,小刘和小周分别站在正方形的对角A C两点处,小刘以的速度走向点D处,途中位置记为P;小周以的速度走向点B处,途中位置记为Q.已知正方形的边长为,E在AB上, ,记三角形AEP的面积为,三角形BEQ的面积为.假设两人同时出发,运动的时间为.
(1)用含t的代数式表示下列线段的长度:
________;________;________;________;
(2)当t为何值时,
(3)他们出发多少秒时,
【答案】(1),,,;(2);(3)
【分析】(1)由路程=速度×时间以及图形中相关线段间的和差关系填空;
(2)根据题意列出方程8 2t=3t,则易求t的值;
(3)利用三角形的面积公式和等量关系列出方程×2t×6=(8 6)×(8 3t),通过解方程易求t的值.
【详解】解:(1)∵小刘以的速度走向点D,∴,则,
∵小周以的速度走向点B处,∴,则,
故答案为:;;;;
(2)由题意,可得,
解得. 即当时,;
(3)设他们出发时,则小刘所走路程为,即;
小周所走路程为,则;
由题意得.
解得, 即他们出发时,.
27、某种海产品,若直接销售,每吨可获利润1200元;若粗加工后销售,每吨可获利润5000元;若精加工后销售,每吨可获利润7500元.某公司现有这种海产品140吨,该公司的生产能力是:如果进行粗加工,每天可加工16吨;如果进行精加工,每天可加工6吨,但两种加工方式不能同时进行,受各种条件限制,公司必须在15天内将这批海产品全部销售或加工完毕,为此该公司设计了三种方案:
方案一:全部进行粗加工;
方案二:尽可能多地进行精加工,没有来得及进行精加工的直接销售;
方案三:将一部分进行精加工,其余的进行粗加工,并恰好15天完成.
你认为选择哪种方案可获利润最多,为什么?最多可获利润多少元?
【答案】方案三可获利润最多,最多可获利润850000元.
【分析】方案一由于全部进行粗加工,而16×15>140,所以粗加工可以全部加工完,然后每吨可获利润5000元即可求出利润;方案二由于尽可能多地进行精加工,没有来得及进行精加工的直接销售,那么15天可精加工6×15=90吨,剩下的直接销售,再根据已知条件也可求出利润;方案三由于将一部分进行精加工,其余的进行粗加工,并恰好15天完成,那么设将x吨海产品进行精加工,则将(140-x)吨进行粗加工,根据恰好15天完成可以列出方程求出精加工和粗加工各自的吨数,然后利用已知条件求出利润.
【详解】
解:方案一:可获利润为:5000×140=700000(元);
方案二:15天可精加工6×15=90(吨),
说明还有50吨需要直接销售,
故可获利润:7500×90+1200×50=735000(元);
方案三:设将x吨海产品进行精加工,则将(140-x)吨进行粗加工,
由题意得:,
解得:x=60,
故可获利润7500×60+5000×80=850000(元),
∵850000>735000>700000,
所以选择方案三可获利润最多,最多可获利润850000元.
28、如图,甲、乙两个圆柱形玻璃容器各盛有一定量的液体,甲、乙容器的内底面半径分别为和,现将一个半径为的圆柱形玻璃棒(足够长)垂直触底插入甲容器,此时甲、乙两个容器的液面高均为(如图①),再将此玻璃棒垂直触底插入乙容器(液体损耗忽略不计),此时乙容器的液面比甲容器的液面高(如图②).
(1)求甲、乙两个容器的内底面面积.
(2)如图①,分别求出甲、乙容器内液体的体积(用含h的代数式表示).
(3)求h的值.
【答案】(1)36πcm2,16πcm2;(2)32πh(cm3),16πh(cm3);(3)
【分析】(1)由甲、乙容器的内底面半径分别为6cm和4cm,可得甲、乙两个容器的内底面面积;
(2)根据题意,即可得甲、乙容器内液体的体积;
(3)根据题意乙的液体体积不变,可列出方程即可求得h的值.
【详解】解:(1)由甲、乙容器的内底面半径分别为6cm和4cm,
所以甲、乙两个容器的内底面面积分别为:36πcm2,16πcm2.
答:甲、乙两个容器的内底面面积分别为:36πcm2,16πcm2.
(2)根据题意,得
甲容器内液体的体积为:36πh-4πh=32πh(cm3);
乙容器内液体的体积为:16πh(cm3);
(3)根据题意可知:
乙的液体体积不变,可得16πh=(16π-4π)(+3)
解得h=,
答:h的值为.
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
