华东师大版七上数学 2.11有理数的乘方 课件(共27张PPT)
文档属性
| 名称 | 华东师大版七上数学 2.11有理数的乘方 课件(共27张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 294.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-28 00:00:00 | ||
图片预览







文档简介
(共27张PPT)
2.11有理数的乘方
——华师版七年级数学(上)
问题情景
同学们,你们一定吃过拉面吧。你在品尝这来自大西北的风味佳肴时,你想过这细长的面条里隐含的数学知识吗?
拉面师傅把一团和好的面,第一次拉伸对折后面条的根数是2,第二次拉伸对折后面条的根数是4,第三次再把它拉长对折,这时面条的根数是8......
按照这种方法,第10次时拉面的总长度是多少米呢?
生活中的拉面的长度涉及哪些数学知识?
学习目标:
1.理解有理数乘方的意义,会进行有理数的乘方运算。
2.经历探索幂的符号法则的过程,会判断幂的符号。
3.在学习过程中,进一步增强观察、归纳概括能力,体会转化的思想。
重点难点:
1.乘方的意义,幂的符号法则;
2.熟练进行有理数的乘方运算。
模块一
自主预学 探索新知
1.预学内容范围:
华师版七年级数学(上)P57-58页(5分钟)
2.预学要求:
(1)认真默读(至少两遍),勾画标注“有理数乘方、幂、底数、指数”的概念。
(2)在勾画标注的基础上默记相关定义、性质。
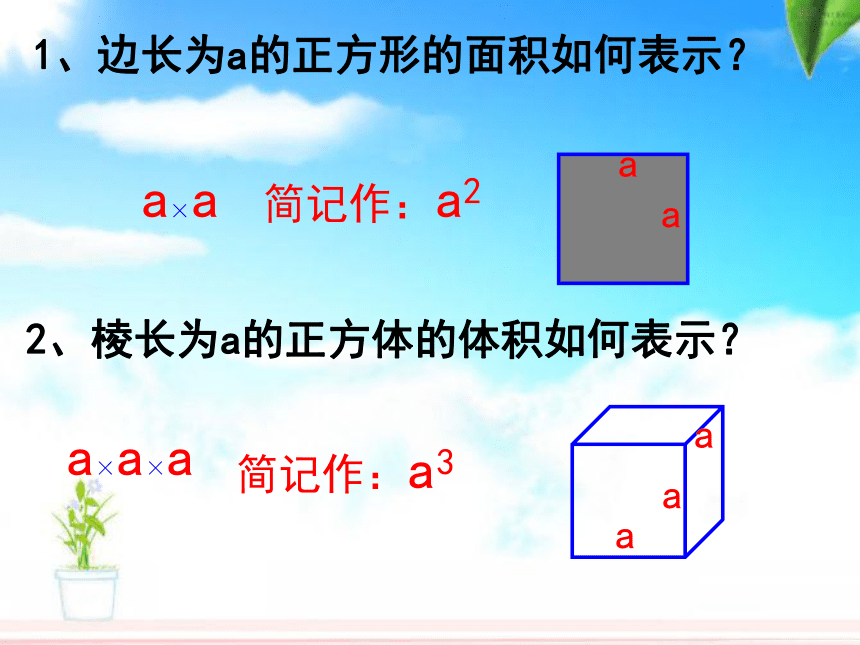
1、边长为a的正方形的面积如何表示?
a×a
简记作:a2
a
a
2、棱长为a的正方体的体积如何表示?
a×a×a
简记作:a3
a
a
a
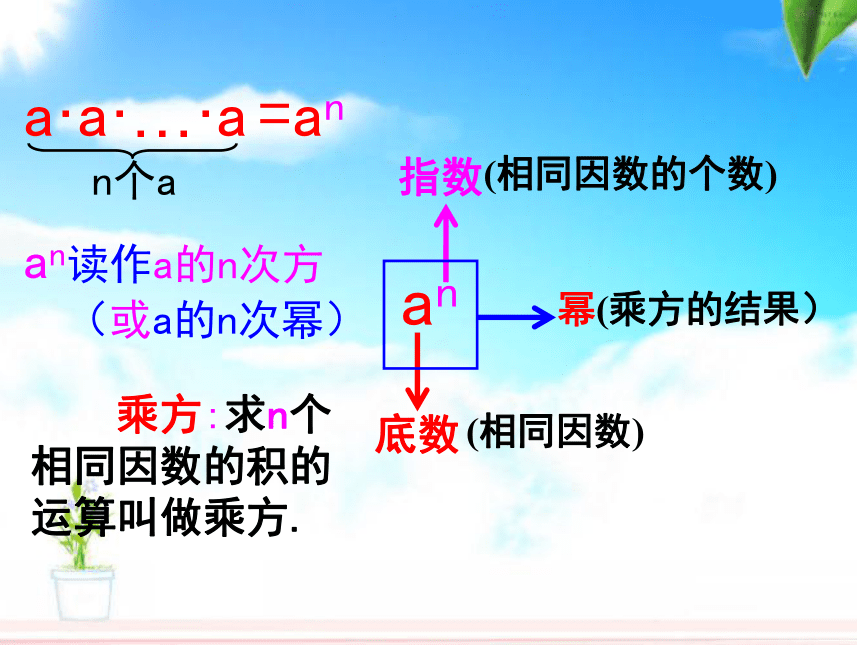
a·a·…·a
=an
n个a
an读作a的n次方
(或a的n次幂)
乘方:求n个相同因数的积的运算叫做乘方.
an
底数
(相同因数)
幂(乘方的结果)
指数
(相同因数的个数)
模块二
活学活用 自主完成
要求:
1. 2-3分钟时间内完成
2. 2分钟时间同桌互相批改并纠错改正。
(1)73中底数是 7 ,指数是 3 .
读作:7的3次方(幂), 意义:3个7相乘
(2)在 中底数是 ,指数是 2 .
读作: 的2次方(幂),意义:2个 相乘
(3)在(-5)4中底数是 -5 ,指数是 4 .
读作:-5的4次方(幂), 意义:4个-5相乘
(4)整数6可以看作底数是 6指数是 1 的幂;
模块三
初试锋芒 收获新知
1.独立解决例题
2.尝试完成“小试牛刀”中的问题
小试牛刀部分错题诊断
正解: 表示6个-2相乘的积,结果是64; 表示3个2相乘的积,结果是8; 表示3个0相乘的积,结果是0。
3. 4人小组讨论:我发现了有理数乘方的计算法则:
正数 ;
负数 ,
负数 。
0的任何正整数次幂 。
有理数的乘方法则
正数的任何次幂都是正数;
负数的奇次幂是负数,
负数的偶次幂是正数;
0的任何正整数次幂都是0。
再接再厉
快速确定下列幂的符号
正 正 正 正 负 正
模块四
小组互动 解疑答惑
(1)
(2)
(3)
说一说,算一算,议一议
1.说一说:上述各组中的两个数的意义,它们相同吗?
2.算一算:各组中两个数的计算结果。
3.议一议:进行有理数的乘方运算时应该注意哪些问题?
拨云见日 水落石出
(1) 表示3个2相乘,结果是8; 表示2个3相乘,结果是9.
(2) 表示4个-2相乘,结果是16; 表示4个2相乘的积的相反数。
(3) 表示2个 相乘的积,结果是
表示2个6相乘的积除以5的商,结果是 。
注意:
1 .乘方是特殊的乘法运算,所谓特殊就是所乘的因数是相同的。
2.幂的底数是分数或负数时,底数应该添上括号。
模块五
快速检测 学有所得
(10分钟)
模块六
课堂小结 收获多多
1.乘方:求几个相同因数的积的运算叫做乘方,乘方的结果叫做幂。
2.有理数乘方运算法则:
正数的任何次幂都是正数;0的任何正整数次幂都是0,负数的奇次幂是负数,负数的偶次幂是正数。
3 .乘方是特殊的乘法运算,所谓特殊就是所乘的因数是相同的。
4.幂的底数是分数或负数时,底数应该添上括号。
我收获了:
情景回归
思考:拉面的数量与拉面次数的关系?
次数 根数 表示方法
1 2
2 4
3 8
...
10 1024
...
2.11有理数的乘方
——华师版七年级数学(上)
问题情景
同学们,你们一定吃过拉面吧。你在品尝这来自大西北的风味佳肴时,你想过这细长的面条里隐含的数学知识吗?
拉面师傅把一团和好的面,第一次拉伸对折后面条的根数是2,第二次拉伸对折后面条的根数是4,第三次再把它拉长对折,这时面条的根数是8......
按照这种方法,第10次时拉面的总长度是多少米呢?
生活中的拉面的长度涉及哪些数学知识?
学习目标:
1.理解有理数乘方的意义,会进行有理数的乘方运算。
2.经历探索幂的符号法则的过程,会判断幂的符号。
3.在学习过程中,进一步增强观察、归纳概括能力,体会转化的思想。
重点难点:
1.乘方的意义,幂的符号法则;
2.熟练进行有理数的乘方运算。
模块一
自主预学 探索新知
1.预学内容范围:
华师版七年级数学(上)P57-58页(5分钟)
2.预学要求:
(1)认真默读(至少两遍),勾画标注“有理数乘方、幂、底数、指数”的概念。
(2)在勾画标注的基础上默记相关定义、性质。
1、边长为a的正方形的面积如何表示?
a×a
简记作:a2
a
a
2、棱长为a的正方体的体积如何表示?
a×a×a
简记作:a3
a
a
a
a·a·…·a
=an
n个a
an读作a的n次方
(或a的n次幂)
乘方:求n个相同因数的积的运算叫做乘方.
an
底数
(相同因数)
幂(乘方的结果)
指数
(相同因数的个数)
模块二
活学活用 自主完成
要求:
1. 2-3分钟时间内完成
2. 2分钟时间同桌互相批改并纠错改正。
(1)73中底数是 7 ,指数是 3 .
读作:7的3次方(幂), 意义:3个7相乘
(2)在 中底数是 ,指数是 2 .
读作: 的2次方(幂),意义:2个 相乘
(3)在(-5)4中底数是 -5 ,指数是 4 .
读作:-5的4次方(幂), 意义:4个-5相乘
(4)整数6可以看作底数是 6指数是 1 的幂;
模块三
初试锋芒 收获新知
1.独立解决例题
2.尝试完成“小试牛刀”中的问题
小试牛刀部分错题诊断
正解: 表示6个-2相乘的积,结果是64; 表示3个2相乘的积,结果是8; 表示3个0相乘的积,结果是0。
3. 4人小组讨论:我发现了有理数乘方的计算法则:
正数 ;
负数 ,
负数 。
0的任何正整数次幂 。
有理数的乘方法则
正数的任何次幂都是正数;
负数的奇次幂是负数,
负数的偶次幂是正数;
0的任何正整数次幂都是0。
再接再厉
快速确定下列幂的符号
正 正 正 正 负 正
模块四
小组互动 解疑答惑
(1)
(2)
(3)
说一说,算一算,议一议
1.说一说:上述各组中的两个数的意义,它们相同吗?
2.算一算:各组中两个数的计算结果。
3.议一议:进行有理数的乘方运算时应该注意哪些问题?
拨云见日 水落石出
(1) 表示3个2相乘,结果是8; 表示2个3相乘,结果是9.
(2) 表示4个-2相乘,结果是16; 表示4个2相乘的积的相反数。
(3) 表示2个 相乘的积,结果是
表示2个6相乘的积除以5的商,结果是 。
注意:
1 .乘方是特殊的乘法运算,所谓特殊就是所乘的因数是相同的。
2.幂的底数是分数或负数时,底数应该添上括号。
模块五
快速检测 学有所得
(10分钟)
模块六
课堂小结 收获多多
1.乘方:求几个相同因数的积的运算叫做乘方,乘方的结果叫做幂。
2.有理数乘方运算法则:
正数的任何次幂都是正数;0的任何正整数次幂都是0,负数的奇次幂是负数,负数的偶次幂是正数。
3 .乘方是特殊的乘法运算,所谓特殊就是所乘的因数是相同的。
4.幂的底数是分数或负数时,底数应该添上括号。
我收获了:
情景回归
思考:拉面的数量与拉面次数的关系?
次数 根数 表示方法
1 2
2 4
3 8
...
10 1024
...
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
