2021-2022学年 人教版数学八年级上册13.3.1 等腰三角形的判定 课件(共24张PPT)
文档属性
| 名称 | 2021-2022学年 人教版数学八年级上册13.3.1 等腰三角形的判定 课件(共24张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 301.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-28 08:25:47 | ||
图片预览







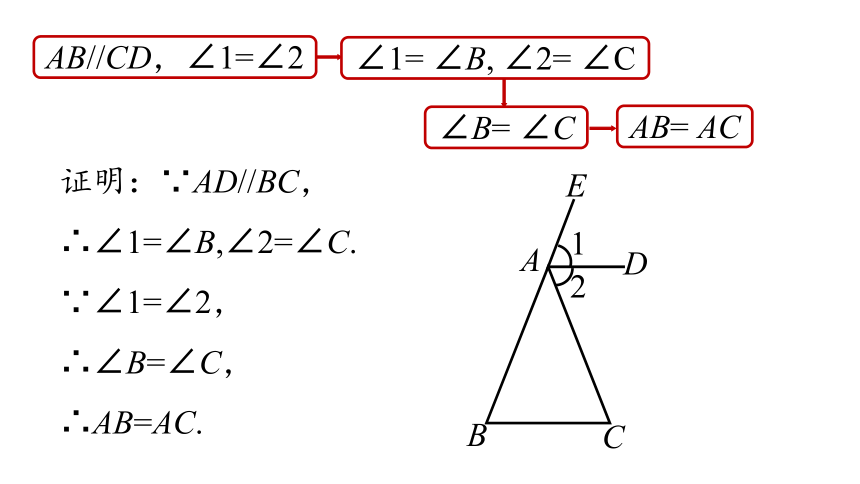
文档简介
(共24张PPT)
人教版 数学 八年级上册
第3节 等腰三角形
第2课时 等腰三角形的判定
第十三章 轴对称
等腰三角形的性质1:等腰三角形的两个底角相等(简写成“等边对等角”).
等腰三角形的性质2:等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合(简写成“三线合一”).
等腰三角形有哪些性质?
复习旧知
我们知道,如果有一个三角形有两条边相等,那么它们所对的角相等.反过来,如果一个三角形有两个角相等,那么它们所对的边有什么关系?
猜想:如果一个三角形有两个角相等,那么它们所对的边相等.
你能证明这个结论吗?
导入新知
证明:如图,作∠BAC的平分线AD交BC于点D,
∴∠BAD=∠CAD.
∵在△ABD和△ACD中,
∠B=∠C,
∠BAD=∠CAD,
AD=AD,
∴△ABD≌△ACD(AAS).∴ AB=AC.
如图,在△ABC中, ∠B=∠C.求证:AB=AC.
A
C
B
D
1.理解等腰三角形的判定,体会等腰三角形“等边对等角”和“等角对等边”的区别.
2.探索并掌握等腰三角形的判定的过程,并用以解决实际问题.
学习目标
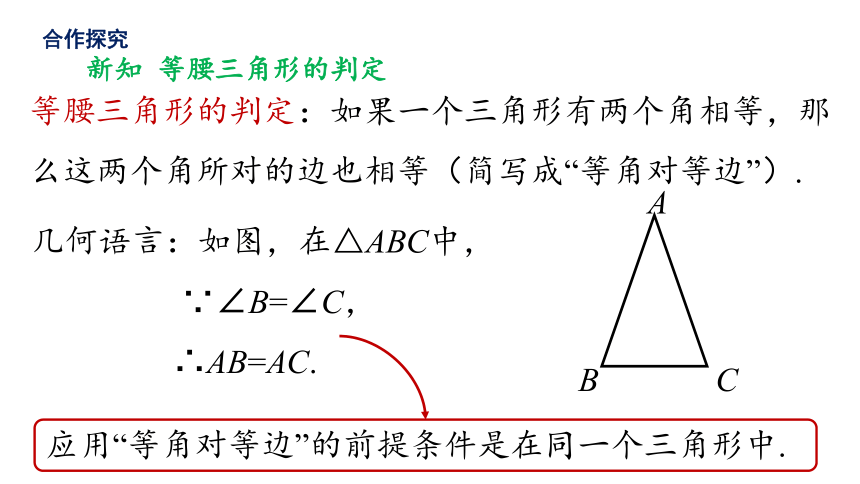
等腰三角形的判定:如果一个三角形有两个角相等,那么这两个角所对的边也相等(简写成“等角对等边”).
几何语言:如图,在△ABC中,
∵∠B=∠C,
∴AB=AC.
A
B
C
新知 等腰三角形的判定
应用“等角对等边”的前提条件是在同一个三角形中.
合作探究
“等边对等角”与“等角对等边”的区别:
等腰三角形的性质:
两边相等 这两边所对的角相等
等腰三角形的判定:
两角相等 这两角所对的边相等
例1 求证:如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形.
分析:命题的证明首先需要将命题转化为已知、求证的格式,再要根据题意画出图形,最后证明结论的成立.
已知:∠CAE是△ABC的外角,∠1=∠2,AD//BC.
求证:AB=AC.
A
B
C
D
E
1
2
典例精析
证明:∵AD//BC,
∴∠1=∠B,∠2=∠C.
∵∠1=∠2,
∴∠B=∠C,
∴AB=AC.
A
B
C
D
E
1
2
AB//CD,∠1=∠2
∠1= ∠B, ∠2= ∠C
∠B= ∠C
AB= AC
作法:(1)作线段AB=a.
(2)作线段AB的垂直平分线MN,
与AB相交于点D.
(3)在MN上取一点C,使得DC=h.
(4)连接AC,BC.
则△ABC就是所求作的等腰三角形.
例2 已知等腰三角形底边长为a,底边上的高的长为h,求作这个等腰三角形.
a
h
A
B
C
D
M
N
解:∵在△ABC中,∠A=36°,∠C=72°,
∴∠ABC=72°.∵∠DBC=36°, ∴∠2=∠ABC-∠DBC=36°.
∵∠1=∠A+∠2=72°,
∴AD=BD=BC,AB=AC.
图中的等腰三角形有△ABC,△ABD,△BCD.
如图,∠A=36°,∠DBC=36°,∠C=72°,分别计∠1,∠2的度数,并说明图中有哪些等腰三角形.
2
1
A
C
D
B
巩固新知
等腰
三角形
判定
综合应用
如果一个三角形有两个角相等,那么这两个角所对的边也相等
将等腰三角形的性质和判定综合应用在解决实际问题中
归纳新知
1.如图,由下列条件不能推出△ABC是等腰三角形的是( )
A.∠B=∠C
B.AD⊥BC,∠BAD=∠CAD
C.AD⊥BC,BD=CD
D.AD⊥BC,∠BAD=∠ACD
D
课后练习
2.如图,∠B=∠C=36°,∠ADE=∠AED=72°,则图中的等腰三角形有( )
A.3个 B.4个
C.5个 D.6个
D
3.如图,在△ABC中,AB=AC,∠BAC=108°,∠ADB=72°,DE平分∠ADB,则图中等腰三角形的个数是( )
A.3 B.4 C.5 D.2
C
C
5.在下列三角形中,若AB=AC,则不能被一条直线分成两个小等腰三角形的是( )
B
C
7.【2020·哈尔滨】已知:在△ABC中,AB=AC,点D、点E在边BC上,BD=CE,连接AD,AE.
(1)如图①,求证AD=AE;
证明:∵AB=AC,∴∠B=∠C.
又∵AB=AC,BD=CE,
∴△ABD≌△ACE(SAS).
∴AD=AE.
(2)如图②,当∠DAE=∠C=45°时,过点B作BF∥AC交AD的延长线于点F,在不添加任何辅助线的情况下,请直接写出图②中的四个等腰三角形,使写出的每个等腰三角形的顶角都等于45°.
解:满足条件的等腰三角形有
△ABE,△ACD,△DAE,
△DBF.
8.【2020·河池】(1)如图①,已知CE与AB交于点E,AC=BC,∠1=∠2.求证△ACE≌△BCE.
(2)如图②,已知CD的延长线与AB交于点E,AD=BC,∠3=∠4.探究AE与BE的数量关系,并说明理由.
解:AE=BE.理由如下:
如图,在CE上取点F,使CF=DE,连接BF.
易得△ADE≌△BCF(SAS),
∴AE=BF,∠AED=∠CFB.
∵∠AED+∠BEF=180°,∠CFB+∠EFB=180°,∴∠BEF=∠EFB.
∴BE=BF.∴AE=BE.
再 见
人教版 数学 八年级上册
第3节 等腰三角形
第2课时 等腰三角形的判定
第十三章 轴对称
等腰三角形的性质1:等腰三角形的两个底角相等(简写成“等边对等角”).
等腰三角形的性质2:等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合(简写成“三线合一”).
等腰三角形有哪些性质?
复习旧知
我们知道,如果有一个三角形有两条边相等,那么它们所对的角相等.反过来,如果一个三角形有两个角相等,那么它们所对的边有什么关系?
猜想:如果一个三角形有两个角相等,那么它们所对的边相等.
你能证明这个结论吗?
导入新知
证明:如图,作∠BAC的平分线AD交BC于点D,
∴∠BAD=∠CAD.
∵在△ABD和△ACD中,
∠B=∠C,
∠BAD=∠CAD,
AD=AD,
∴△ABD≌△ACD(AAS).∴ AB=AC.
如图,在△ABC中, ∠B=∠C.求证:AB=AC.
A
C
B
D
1.理解等腰三角形的判定,体会等腰三角形“等边对等角”和“等角对等边”的区别.
2.探索并掌握等腰三角形的判定的过程,并用以解决实际问题.
学习目标
等腰三角形的判定:如果一个三角形有两个角相等,那么这两个角所对的边也相等(简写成“等角对等边”).
几何语言:如图,在△ABC中,
∵∠B=∠C,
∴AB=AC.
A
B
C
新知 等腰三角形的判定
应用“等角对等边”的前提条件是在同一个三角形中.
合作探究
“等边对等角”与“等角对等边”的区别:
等腰三角形的性质:
两边相等 这两边所对的角相等
等腰三角形的判定:
两角相等 这两角所对的边相等
例1 求证:如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形.
分析:命题的证明首先需要将命题转化为已知、求证的格式,再要根据题意画出图形,最后证明结论的成立.
已知:∠CAE是△ABC的外角,∠1=∠2,AD//BC.
求证:AB=AC.
A
B
C
D
E
1
2
典例精析
证明:∵AD//BC,
∴∠1=∠B,∠2=∠C.
∵∠1=∠2,
∴∠B=∠C,
∴AB=AC.
A
B
C
D
E
1
2
AB//CD,∠1=∠2
∠1= ∠B, ∠2= ∠C
∠B= ∠C
AB= AC
作法:(1)作线段AB=a.
(2)作线段AB的垂直平分线MN,
与AB相交于点D.
(3)在MN上取一点C,使得DC=h.
(4)连接AC,BC.
则△ABC就是所求作的等腰三角形.
例2 已知等腰三角形底边长为a,底边上的高的长为h,求作这个等腰三角形.
a
h
A
B
C
D
M
N
解:∵在△ABC中,∠A=36°,∠C=72°,
∴∠ABC=72°.∵∠DBC=36°, ∴∠2=∠ABC-∠DBC=36°.
∵∠1=∠A+∠2=72°,
∴AD=BD=BC,AB=AC.
图中的等腰三角形有△ABC,△ABD,△BCD.
如图,∠A=36°,∠DBC=36°,∠C=72°,分别计∠1,∠2的度数,并说明图中有哪些等腰三角形.
2
1
A
C
D
B
巩固新知
等腰
三角形
判定
综合应用
如果一个三角形有两个角相等,那么这两个角所对的边也相等
将等腰三角形的性质和判定综合应用在解决实际问题中
归纳新知
1.如图,由下列条件不能推出△ABC是等腰三角形的是( )
A.∠B=∠C
B.AD⊥BC,∠BAD=∠CAD
C.AD⊥BC,BD=CD
D.AD⊥BC,∠BAD=∠ACD
D
课后练习
2.如图,∠B=∠C=36°,∠ADE=∠AED=72°,则图中的等腰三角形有( )
A.3个 B.4个
C.5个 D.6个
D
3.如图,在△ABC中,AB=AC,∠BAC=108°,∠ADB=72°,DE平分∠ADB,则图中等腰三角形的个数是( )
A.3 B.4 C.5 D.2
C
C
5.在下列三角形中,若AB=AC,则不能被一条直线分成两个小等腰三角形的是( )
B
C
7.【2020·哈尔滨】已知:在△ABC中,AB=AC,点D、点E在边BC上,BD=CE,连接AD,AE.
(1)如图①,求证AD=AE;
证明:∵AB=AC,∴∠B=∠C.
又∵AB=AC,BD=CE,
∴△ABD≌△ACE(SAS).
∴AD=AE.
(2)如图②,当∠DAE=∠C=45°时,过点B作BF∥AC交AD的延长线于点F,在不添加任何辅助线的情况下,请直接写出图②中的四个等腰三角形,使写出的每个等腰三角形的顶角都等于45°.
解:满足条件的等腰三角形有
△ABE,△ACD,△DAE,
△DBF.
8.【2020·河池】(1)如图①,已知CE与AB交于点E,AC=BC,∠1=∠2.求证△ACE≌△BCE.
(2)如图②,已知CD的延长线与AB交于点E,AD=BC,∠3=∠4.探究AE与BE的数量关系,并说明理由.
解:AE=BE.理由如下:
如图,在CE上取点F,使CF=DE,连接BF.
易得△ADE≌△BCF(SAS),
∴AE=BF,∠AED=∠CFB.
∵∠AED+∠BEF=180°,∠CFB+∠EFB=180°,∴∠BEF=∠EFB.
∴BE=BF.∴AE=BE.
再 见
