2021-2022学年华东师大版数学九年级上册23.4 三角形的中位线 课件(17张)
文档属性
| 名称 | 2021-2022学年华东师大版数学九年级上册23.4 三角形的中位线 课件(17张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-28 00:00:00 | ||
图片预览



文档简介
(共17张PPT)
自主学习,主动探究
任意一张三角形纸片,能否只剪一刀,使分成的两部分拼成一个平行四边形
A
B
C
D
E
F
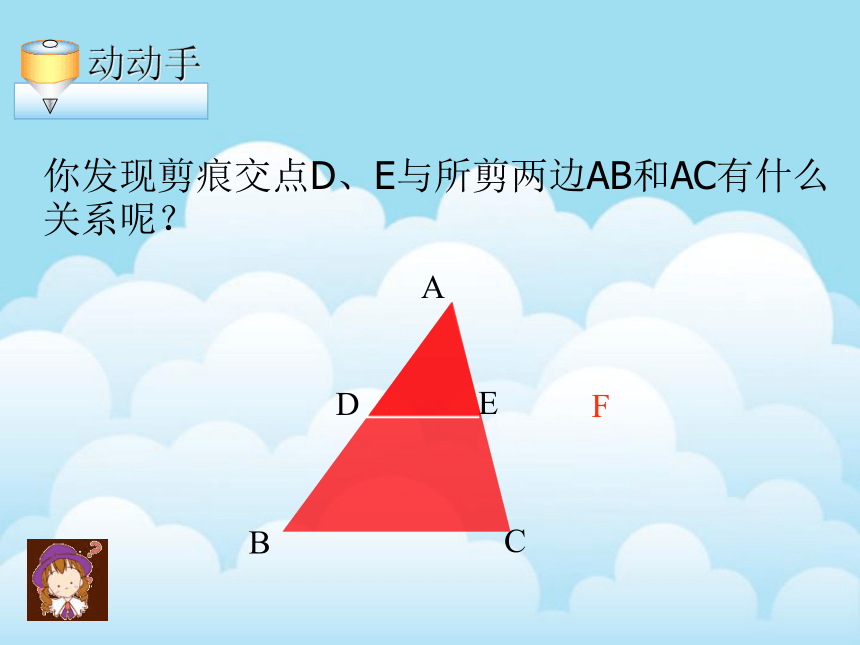
动动手
你发现剪痕交点D、E与所剪两边AB和AC有什么关系呢?
华师大版 九年级(上)
第23章 图形的相似
23.4 三角形的中位线(1)
3条
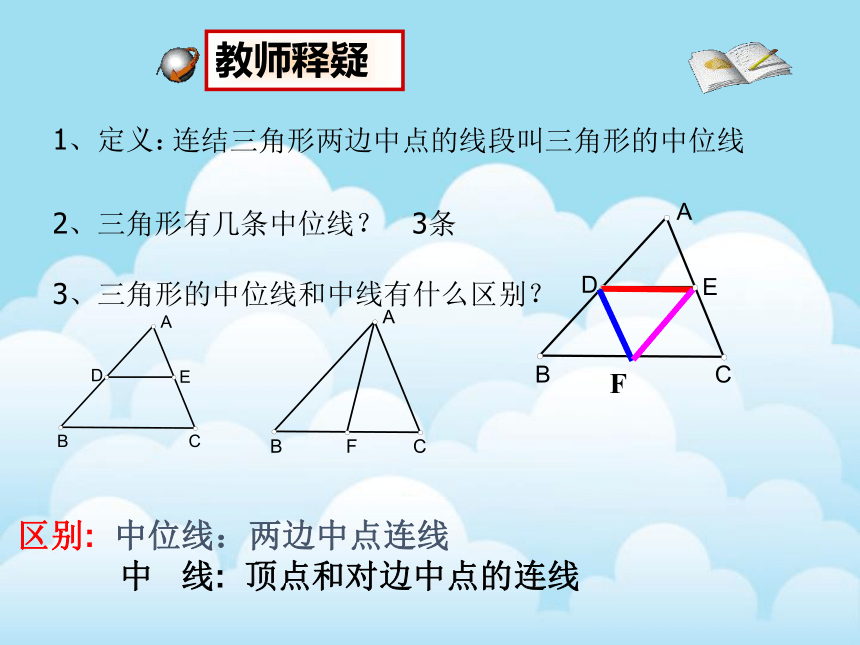
1、定义:
2、三角形有几条中位线?
教师释疑
F
3、三角形的中位线和中线有什么区别?
区别: 中位线:两边中点连线
中 线: 顶点和对边中点的连线
连结三角形两边中点的线段叫三角形的中位线
1、通过测量你发现DE与BC有怎样的数量关系?
2、用量角器量一量∠ADE与∠B的度数,你发现DE与BC有怎样的位置关系?
C
B
A
E
D
活动二
C
B
A
E
D
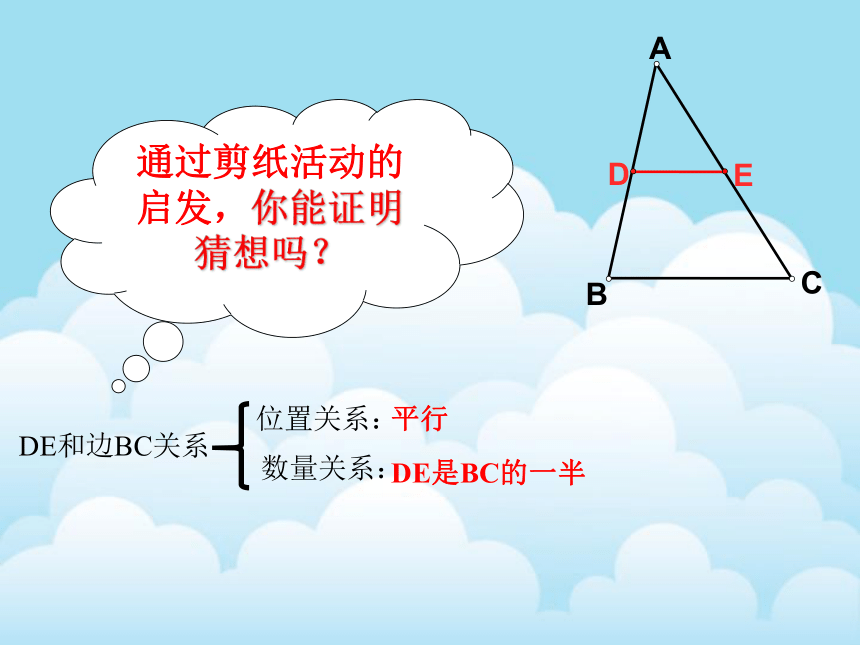
DE和边BC关系
位置关系:
平行
数量关系:
DE是BC的一半
通过剪纸活动的启发,你能证明猜想吗?
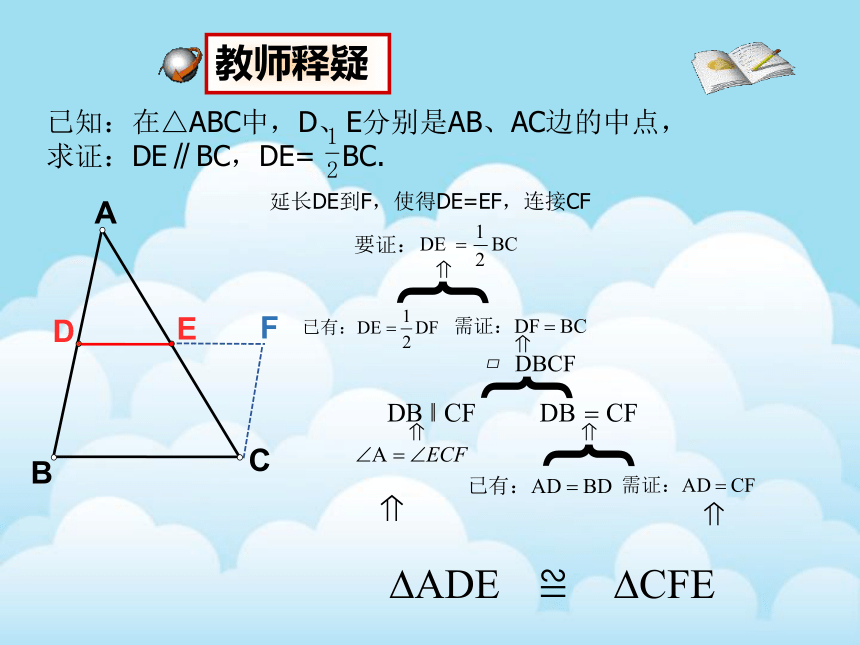
已知:在△ABC中,D、E分别是AB、AC边的中点,
求证:DE∥BC,DE= BC.
C
B
A
E
D
F
教师释疑
延长DE到F,使得DE=EF,连接CF
要证:
︷
︷
︷
≌
已知:在△ABC中,D、E分别是AB、AC边的中点,
求证:DE∥BC,DE= BC.
C
B
A
E
D
F
∥
∥
∥
教师释疑
求证:DE∥BC,DE= BC.
C
B
A
E
D
是否还有其他的证明方法?
已知:在△ABC中,D、E分别是AB、AC边的中点。
教师释疑
已知:在△ABC中,D、E分别是AB、AC边的中点,
求证:DE∥BC,DE= BC.
C
B
A
E
D
∽
∥
教师释疑
定理:三角形的中位线______于第三边,并且等于第三边的______.
∵ D、E分别是AB、AC边的中点,
∴ DE∥BC,DE= BC.
C
B
A
E
D
三角形中位线定理为证明平行关系及线段之间的倍半关系提供了一个新的途径。
几何语言:
教师释疑
平行
一半
C
A
B
M
N
1、现想测量A、B两地之间的距离,但由于有山阻隔,便在AB外选一点C,使C能直接到达A和B,连结AC和BC,并分别找出AC和BC的中点M、N.测出MN=35m,就可知AB=___m
70
学以致用、能力提升
2、如图:在△ABC中,DE是中位线:
①若∠A=40°, ∠B=60°.
则∠AED= 度.
80
A
B
C
D
E
学以致用、能力提升
②△ADE与△ABC的面积之比为
1:4
例:求证三角形的一条中位线与第三边的中线互相平分
A
B
C
D
F
E
已知:如图所示,在△ABC中,D、E、F分别是AB、BC、AC的中点
求证:AE、DF互相平分
要证:AE、DF互相平分
构建知识体系
︷
3、 已知:在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点.
求证:四边形EFGH是平行四边形.
A
C
B
D
H
G
F
E
结论:任意四边形的中点四边形是平行四边形。
学以致用、能力提升
若改变原四边形的形状,那么中点四边形会怎么变呢?
方法总结
1、三角形中位线定理为证明平行关系及线段之间的倍半关系提供了一个新的途径。
2、在处理问题时:
①有三角形两边中点,要连结两边中点得中位线;
②有中点连线而无三角形,要构造三角形。
分层布置作业
A.教材P79 练习2 ,习题2、3、4
B.<实践与探究丛书> P57 例1,例2,变式训练2
自主学习,主动探究
任意一张三角形纸片,能否只剪一刀,使分成的两部分拼成一个平行四边形
A
B
C
D
E
F
动动手
你发现剪痕交点D、E与所剪两边AB和AC有什么关系呢?
华师大版 九年级(上)
第23章 图形的相似
23.4 三角形的中位线(1)
3条
1、定义:
2、三角形有几条中位线?
教师释疑
F
3、三角形的中位线和中线有什么区别?
区别: 中位线:两边中点连线
中 线: 顶点和对边中点的连线
连结三角形两边中点的线段叫三角形的中位线
1、通过测量你发现DE与BC有怎样的数量关系?
2、用量角器量一量∠ADE与∠B的度数,你发现DE与BC有怎样的位置关系?
C
B
A
E
D
活动二
C
B
A
E
D
DE和边BC关系
位置关系:
平行
数量关系:
DE是BC的一半
通过剪纸活动的启发,你能证明猜想吗?
已知:在△ABC中,D、E分别是AB、AC边的中点,
求证:DE∥BC,DE= BC.
C
B
A
E
D
F
教师释疑
延长DE到F,使得DE=EF,连接CF
要证:
︷
︷
︷
≌
已知:在△ABC中,D、E分别是AB、AC边的中点,
求证:DE∥BC,DE= BC.
C
B
A
E
D
F
∥
∥
∥
教师释疑
求证:DE∥BC,DE= BC.
C
B
A
E
D
是否还有其他的证明方法?
已知:在△ABC中,D、E分别是AB、AC边的中点。
教师释疑
已知:在△ABC中,D、E分别是AB、AC边的中点,
求证:DE∥BC,DE= BC.
C
B
A
E
D
∽
∥
教师释疑
定理:三角形的中位线______于第三边,并且等于第三边的______.
∵ D、E分别是AB、AC边的中点,
∴ DE∥BC,DE= BC.
C
B
A
E
D
三角形中位线定理为证明平行关系及线段之间的倍半关系提供了一个新的途径。
几何语言:
教师释疑
平行
一半
C
A
B
M
N
1、现想测量A、B两地之间的距离,但由于有山阻隔,便在AB外选一点C,使C能直接到达A和B,连结AC和BC,并分别找出AC和BC的中点M、N.测出MN=35m,就可知AB=___m
70
学以致用、能力提升
2、如图:在△ABC中,DE是中位线:
①若∠A=40°, ∠B=60°.
则∠AED= 度.
80
A
B
C
D
E
学以致用、能力提升
②△ADE与△ABC的面积之比为
1:4
例:求证三角形的一条中位线与第三边的中线互相平分
A
B
C
D
F
E
已知:如图所示,在△ABC中,D、E、F分别是AB、BC、AC的中点
求证:AE、DF互相平分
要证:AE、DF互相平分
构建知识体系
︷
3、 已知:在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点.
求证:四边形EFGH是平行四边形.
A
C
B
D
H
G
F
E
结论:任意四边形的中点四边形是平行四边形。
学以致用、能力提升
若改变原四边形的形状,那么中点四边形会怎么变呢?
方法总结
1、三角形中位线定理为证明平行关系及线段之间的倍半关系提供了一个新的途径。
2、在处理问题时:
①有三角形两边中点,要连结两边中点得中位线;
②有中点连线而无三角形,要构造三角形。
分层布置作业
A.教材P79 练习2 ,习题2、3、4
B.<实践与探究丛书> P57 例1,例2,变式训练2
