2021-2022学年九年级数学人教版上册23.1图形的旋转 第2课时 旋转作图课件(20张)
文档属性
| 名称 | 2021-2022学年九年级数学人教版上册23.1图形的旋转 第2课时 旋转作图课件(20张) |

|
|
| 格式 | zip | ||
| 文件大小 | 471.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-28 00:00:00 | ||
图片预览





文档简介
(共20张PPT)
23.1 图形的旋转
第二十三章 旋转
第2课时 旋转作图
九年级数学上(RJ)
学习目标
1.按要求作出简单平面图形旋转后的图形。(重点)
2.体验图形旋转产生的数学美。
复习巩固:
平面内,将一个图形绕着一个定点沿某个方向转动一个角度,这样的图形运动称为旋转.
对应点到旋转中心的距离相等。
对应点与旋转中心所连线段的夹角等于旋转角。
旋转前、后的图形全等。
1.旋转的定义:
2.旋转的基本性质:
1.如图,画出线段 AB绕点A按顺时针方向旋转90°后的线段.
P
B'
简单的旋转作图
一
做法:
1.将直线 AB绕点A按顺时针方向旋转90°。
2.在直线AP上截AB'=AB。
3.线段AB'即为所求。
B
A
B
A
C
C
O
100
0
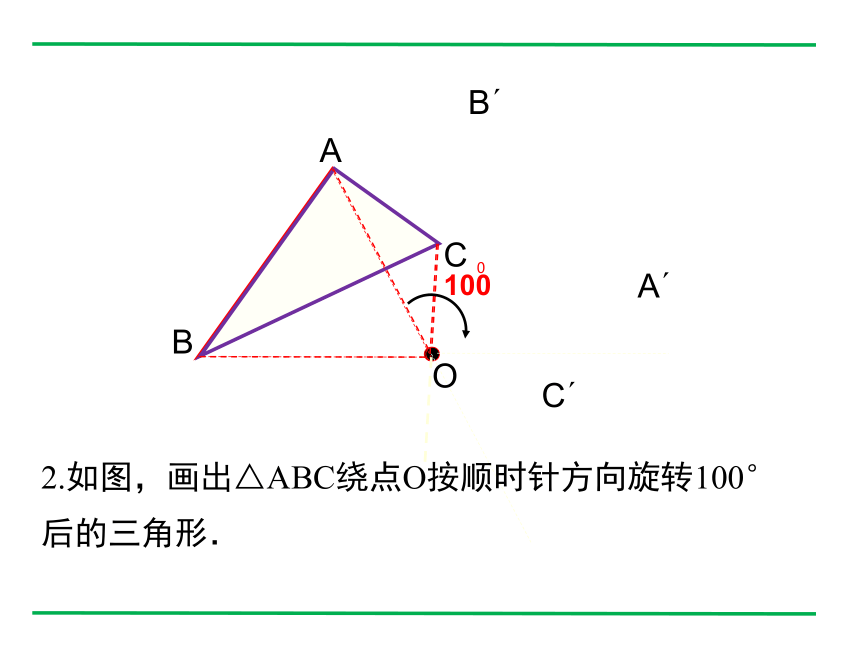
2.如图,画出△ABC绕点O按顺时针方向旋转100°后的三角形.
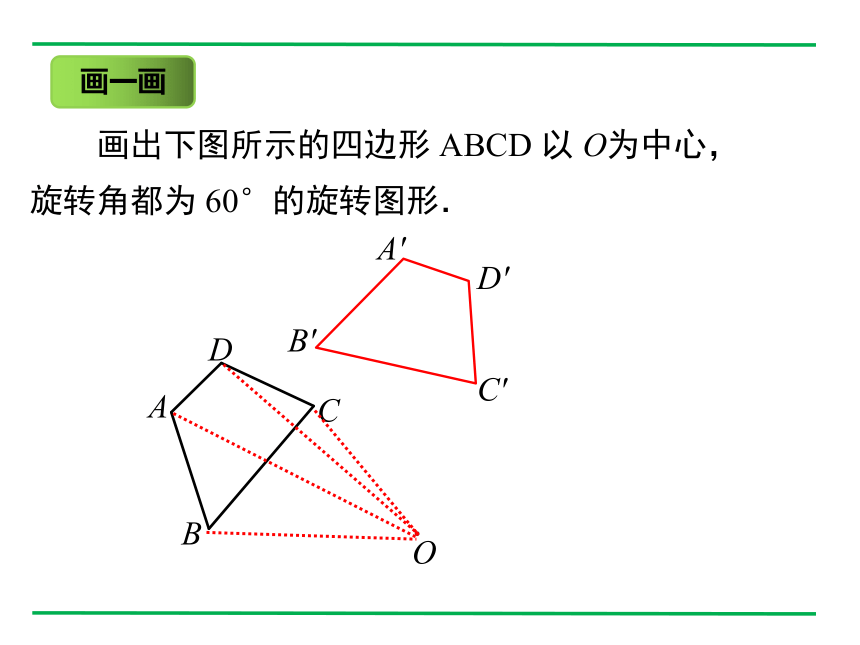
画出下图所示的四边形 ABCD 以 O为中心,
旋转角都为 60°的旋转图形.
A
B
C
D
O
B'
A'
C'
D'
画一画
D
A
B
C
E
E ′
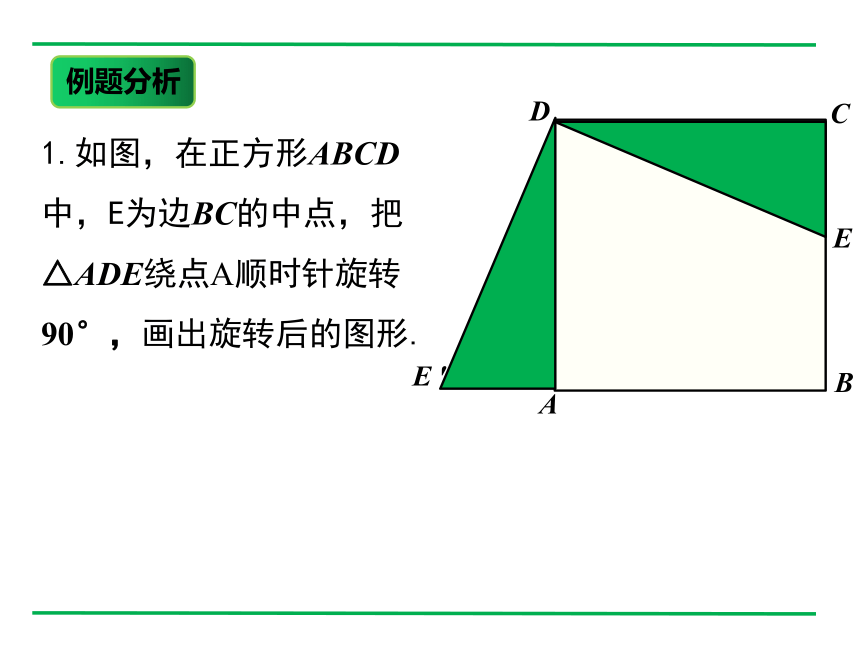
1.如图,在正方形ABCD中,E为边BC的中点,把△ADE绕点A顺时针旋转90°,画出旋转后的图形.
例题分析
1.找出旋转中心、旋转方向和旋转角度.
旋转作图的基本步骤:
2.找到顶点及点的对应点;
3.连接各对应点,作出新图形;
知识要点
D
E
B
F
C
A
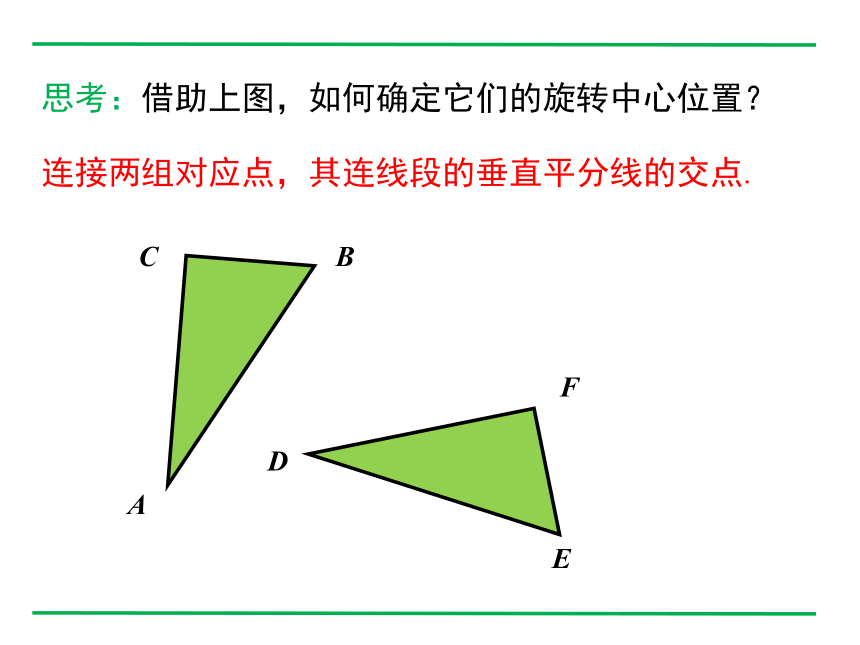
思考:借助上图,如何确定它们的旋转中心位置?
连接两组对应点,其连线段的垂直平分线的交点.
练一练:下图为 4×4 的正方形网格,每个小正方形的边长均为 1,将 △ABC 绕点 A顺时针旋转 90°, 你能画出 旋转后的图形 △AB'C'吗?
A
C'
C
B'
B
1.我们可以借助旋转可以设计出许多美丽的图案.
旋转设计作图
二
对于同一个图形:
如果选择的旋转中心不同,旋转角不同那么会出现不同的效果;
如果旋转中心相同,但旋转角不同,最后呈现的效果也不同。
如果旋转角相同,当选择的旋转中心不同时,最后的效果也不同。
当堂练习
1.下列运动属于旋转的是( )
A.传送带运送医疗器械
B.电梯升降
C.荡秋千
D.雪地滑雪
C
2.把Rt△AOB绕点逆时针旋转得到Rt△A'OB',则旋转角是( )
O
A
B
A'
B'
90°
3.下列说法错误的是( )
A.旋转过程中,对应点到旋转中心的距离相等
B.旋转前后的图形一定全等
C.全等的图形一定是由旋转得到
D.旋转过程中,图形上每一点旋转的角度都相等
C
4.把CD为5的矩形ABCD绕点D逆时针旋转,得到矩形DEFG,点A的对应点E落在边BC上,且CE=EF,则AD的长度为( )
D
A
B
C
E
F
G
5√2
5.根据要求画出旋转后的三角形。
A
C1
C
B1
B
(1)将 △ABC 绕点 O逆时针旋转 90°后的 △A1B1C1.
O
A1
A
C2
C
B2
B
(2)将 △ABC 绕点 O旋转 180°后的 △A2B2C2.
O
A2
6.根据要求画出旋转后的四边形。
将 四边形绕点 O顺时针旋转 90°后的四边形。
O
课堂小结
旋转的作图
1.作旋转图形;
2.找旋转中心:找两条对应点连线段的垂直平分线的交点
23.1 图形的旋转
第二十三章 旋转
第2课时 旋转作图
九年级数学上(RJ)
学习目标
1.按要求作出简单平面图形旋转后的图形。(重点)
2.体验图形旋转产生的数学美。
复习巩固:
平面内,将一个图形绕着一个定点沿某个方向转动一个角度,这样的图形运动称为旋转.
对应点到旋转中心的距离相等。
对应点与旋转中心所连线段的夹角等于旋转角。
旋转前、后的图形全等。
1.旋转的定义:
2.旋转的基本性质:
1.如图,画出线段 AB绕点A按顺时针方向旋转90°后的线段.
P
B'
简单的旋转作图
一
做法:
1.将直线 AB绕点A按顺时针方向旋转90°。
2.在直线AP上截AB'=AB。
3.线段AB'即为所求。
B
A
B
A
C
C
O
100
0
2.如图,画出△ABC绕点O按顺时针方向旋转100°后的三角形.
画出下图所示的四边形 ABCD 以 O为中心,
旋转角都为 60°的旋转图形.
A
B
C
D
O
B'
A'
C'
D'
画一画
D
A
B
C
E
E ′
1.如图,在正方形ABCD中,E为边BC的中点,把△ADE绕点A顺时针旋转90°,画出旋转后的图形.
例题分析
1.找出旋转中心、旋转方向和旋转角度.
旋转作图的基本步骤:
2.找到顶点及点的对应点;
3.连接各对应点,作出新图形;
知识要点
D
E
B
F
C
A
思考:借助上图,如何确定它们的旋转中心位置?
连接两组对应点,其连线段的垂直平分线的交点.
练一练:下图为 4×4 的正方形网格,每个小正方形的边长均为 1,将 △ABC 绕点 A顺时针旋转 90°, 你能画出 旋转后的图形 △AB'C'吗?
A
C'
C
B'
B
1.我们可以借助旋转可以设计出许多美丽的图案.
旋转设计作图
二
对于同一个图形:
如果选择的旋转中心不同,旋转角不同那么会出现不同的效果;
如果旋转中心相同,但旋转角不同,最后呈现的效果也不同。
如果旋转角相同,当选择的旋转中心不同时,最后的效果也不同。
当堂练习
1.下列运动属于旋转的是( )
A.传送带运送医疗器械
B.电梯升降
C.荡秋千
D.雪地滑雪
C
2.把Rt△AOB绕点逆时针旋转得到Rt△A'OB',则旋转角是( )
O
A
B
A'
B'
90°
3.下列说法错误的是( )
A.旋转过程中,对应点到旋转中心的距离相等
B.旋转前后的图形一定全等
C.全等的图形一定是由旋转得到
D.旋转过程中,图形上每一点旋转的角度都相等
C
4.把CD为5的矩形ABCD绕点D逆时针旋转,得到矩形DEFG,点A的对应点E落在边BC上,且CE=EF,则AD的长度为( )
D
A
B
C
E
F
G
5√2
5.根据要求画出旋转后的三角形。
A
C1
C
B1
B
(1)将 △ABC 绕点 O逆时针旋转 90°后的 △A1B1C1.
O
A1
A
C2
C
B2
B
(2)将 △ABC 绕点 O旋转 180°后的 △A2B2C2.
O
A2
6.根据要求画出旋转后的四边形。
将 四边形绕点 O顺时针旋转 90°后的四边形。
O
课堂小结
旋转的作图
1.作旋转图形;
2.找旋转中心:找两条对应点连线段的垂直平分线的交点
同课章节目录
