2021-2022学年人教版数学八年级上册13.2.1 画轴对称图形(共25张PPT)
文档属性
| 名称 | 2021-2022学年人教版数学八年级上册13.2.1 画轴对称图形(共25张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 391.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-28 00:00:00 | ||
图片预览






文档简介
(共25张PPT)
人教版 数学 八年级上册
第2节 画轴对称图形
第1课时 画轴对称图形
第十三章 轴对称
前面我们已经学习了画一个轴对称图形或两个成轴对称的图形的对称轴,如果有一个图形和一条直线,如何画出这个图形关于这条直线对称的图形呢?
导入新知
1.理解图形轴对称变换的性质.
2.能够按照要求画出一个平面图形关于某条直线对称的图形.
学习目标
如图,在一张半透明的纸的左边部分,画一只左脚印.把这张纸对折后描图,打开对折的纸,就能得到相应的右脚印.
新知 画轴对称图形
(1)认真观察,左脚印和右脚印有什么关系?
由一个平面图形可以得到与它关于一条直线 l 对称的图形,这个图形与原图形的形状、大小完全相同.
合作探究
(2)对称轴是折痕所在的直线,即直线l,它与图中的线段PP′是什么关系?
新图形上的每一点都是原图形上的某一点关于直线l的对称点;
连接任意一对对应点的线段被对称轴垂直平分.
请你动手再画一个图形,看看能否得到相同的结论?
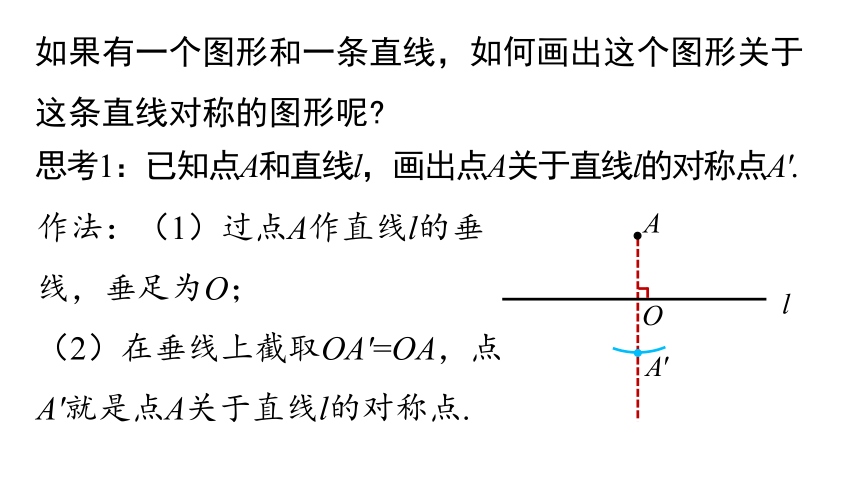
思考1:已知点A和直线l,画出点A关于直线l的对称点A′.
作法:(1)过点A作直线l的垂线,垂足为O;
(2)在垂线上截取OA′=OA,点A′就是点A关于直线l的对称点.
l
A
A′
O
如果有一个图形和一条直线,如何画出这个图形关于这条直线对称的图形呢
l
B
思考2:已知线段AB和直线l,画出线段AB关于直线l的对称线段A′B′.
作法:(1)过点A作直线l的垂线,垂足为O,在垂线上截取OA′=OA,点A′就是点A关于直线l的对称点.
(2)过点B作直线l的垂线,垂足为P,在垂线上截取PB′=PB,点B′就是点B关于直线l的对称点.
(3)连接A′B′,则线段A′B′即为所求.
A′
B′
A
O
P
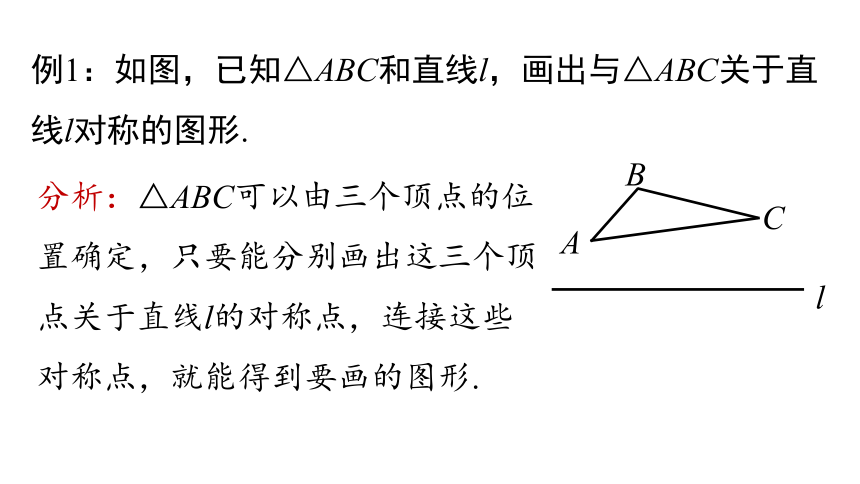
例1:如图,已知△ABC和直线l,画出与△ABC关于直线l对称的图形.
分析:△ABC可以由三个顶点的位置确定,只要能分别画出这三个顶点关于直线l的对称点,连接这些对称点,就能得到要画的图形.
l
C
A
B
O
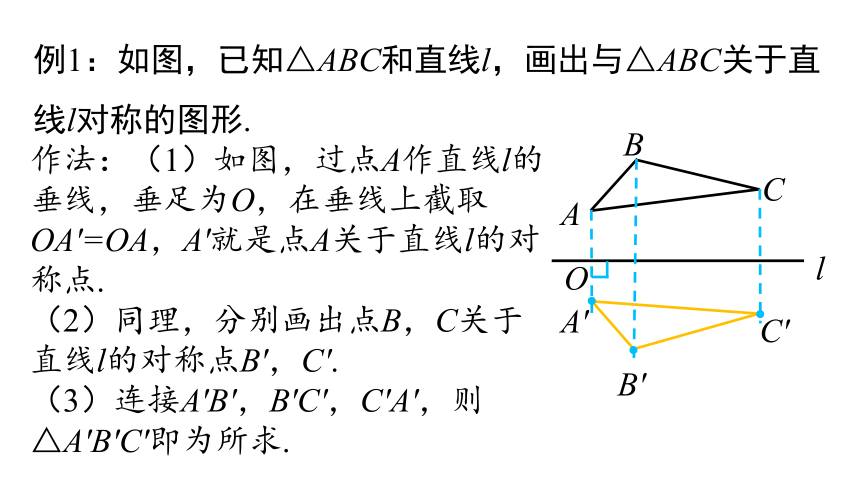
例1:如图,已知△ABC和直线l,画出与△ABC关于直线l对称的图形.
作法:(1)如图,过点A作直线l的垂线,垂足为O,在垂线上截取OA′=OA,A′就是点A关于直线l的对称点.
(2)同理,分别画出点B,C关于直线l的对称点B′,C′.
(3)连接A′B′,B′C′,C′A′,则△A′B′C′即为所求.
l
C
C′
A′
B′
B
A
画轴对称图形的方法
找:在原图形上找特殊点;
画:画出各个特殊点关于对称轴的对称点;
连:连接这些对称点,就可以得到原图形的轴对称图形.
线段的端点,线与线的交点、中点等
如图,把下列图形补成关于直线 l 对称的轴对称图形.
l
l
作轴对称图形的口诀:作垂线,截等线,顺次连.
典例精析
画轴对称图形
轴对称变换
轴对称变换的性质
画出已知图形的轴对称图形
成轴对称的两个图形全等
1.新旧图形的对应点是对称点;
2.连接对应点的线段被对称轴垂直平分
一找,二画,三连
归纳新知
1.下列说法正确的是( )
A.全等的两个图形是由其中一个经过轴对称变换得到的
B.轴对称变换得到的图形与原图形全等
C.轴对称变换中的两个图形,每一对对应点所连线段都被这两个图形之间的直线垂直平分
D.轴对称变换得到的图形也可以由原图形经过平移得到
B
课后练习
2.如图,△AOD关于直线l进行轴对称变换后得到△BOC,则以下结论中不正确的是( )
A.∠1=∠2
B.∠3=∠4
C.l垂直平分AB,且l垂直平分CD
D.AC与BD互相平分
D
3.如图所示是一只停泊在平静水面上的小船,它的“倒影”应是( )
B
4.下列图形中,分别以直线l为对称轴作轴对称,其中错误的是( )
C
5.下面是四名同学作△ABC关于直线MN的轴对称图形,其中正确的是( )
B
6.如图,在由4个小正方形组成的田字格中,△ABC的顶点都是小正方形的顶点,在田字格上画与△ABC成轴对称的三角形,且顶点都是小正方形的顶点,则这样的三角形(不包含△ABC本身)共有( )
A.1个 B.3个 C.2个 D.4个
B
7.如图,正三角形网格中,已有两个小三角形被涂黑.
(1)再将图①中其余小三角形涂黑一个,使整个被涂黑的图案构成一个轴对称图形(画出两种不同的);
解:如图①所示.
(2)再将图②中其余小三角形涂黑两个,使整个被涂黑的图案构成一个轴对称图形(画出两种不同的).
解:如图②所示.
(答案不唯一.)
8.【2020·吉林】图①、图②、图③都是3×3的正方形网格,每个小正方形的顶点称为格点.A,B,C均为格点,在给定的网格中,按下列要求画图:
(1)在图①中,画一条不与AB重合的线段MN,使MN与AB关于某条直线对称,且M,N为格点;
解:如图①,MN即为所求.(答案不唯一)
(2)在图②中,画一条不与AC重合的线段PQ,使PQ与AC关于某条直线对称,且P,Q为格点;
解:如图②,PQ
即为所求.(答案不唯一)
(3)在图③中,画一个△DEF,使△DEF与△ABC关于某条直线对称,且D,E,F为格点.
解:如图③,△DEF即为所求.(答案不唯一)
再 见
人教版 数学 八年级上册
第2节 画轴对称图形
第1课时 画轴对称图形
第十三章 轴对称
前面我们已经学习了画一个轴对称图形或两个成轴对称的图形的对称轴,如果有一个图形和一条直线,如何画出这个图形关于这条直线对称的图形呢?
导入新知
1.理解图形轴对称变换的性质.
2.能够按照要求画出一个平面图形关于某条直线对称的图形.
学习目标
如图,在一张半透明的纸的左边部分,画一只左脚印.把这张纸对折后描图,打开对折的纸,就能得到相应的右脚印.
新知 画轴对称图形
(1)认真观察,左脚印和右脚印有什么关系?
由一个平面图形可以得到与它关于一条直线 l 对称的图形,这个图形与原图形的形状、大小完全相同.
合作探究
(2)对称轴是折痕所在的直线,即直线l,它与图中的线段PP′是什么关系?
新图形上的每一点都是原图形上的某一点关于直线l的对称点;
连接任意一对对应点的线段被对称轴垂直平分.
请你动手再画一个图形,看看能否得到相同的结论?
思考1:已知点A和直线l,画出点A关于直线l的对称点A′.
作法:(1)过点A作直线l的垂线,垂足为O;
(2)在垂线上截取OA′=OA,点A′就是点A关于直线l的对称点.
l
A
A′
O
如果有一个图形和一条直线,如何画出这个图形关于这条直线对称的图形呢
l
B
思考2:已知线段AB和直线l,画出线段AB关于直线l的对称线段A′B′.
作法:(1)过点A作直线l的垂线,垂足为O,在垂线上截取OA′=OA,点A′就是点A关于直线l的对称点.
(2)过点B作直线l的垂线,垂足为P,在垂线上截取PB′=PB,点B′就是点B关于直线l的对称点.
(3)连接A′B′,则线段A′B′即为所求.
A′
B′
A
O
P
例1:如图,已知△ABC和直线l,画出与△ABC关于直线l对称的图形.
分析:△ABC可以由三个顶点的位置确定,只要能分别画出这三个顶点关于直线l的对称点,连接这些对称点,就能得到要画的图形.
l
C
A
B
O
例1:如图,已知△ABC和直线l,画出与△ABC关于直线l对称的图形.
作法:(1)如图,过点A作直线l的垂线,垂足为O,在垂线上截取OA′=OA,A′就是点A关于直线l的对称点.
(2)同理,分别画出点B,C关于直线l的对称点B′,C′.
(3)连接A′B′,B′C′,C′A′,则△A′B′C′即为所求.
l
C
C′
A′
B′
B
A
画轴对称图形的方法
找:在原图形上找特殊点;
画:画出各个特殊点关于对称轴的对称点;
连:连接这些对称点,就可以得到原图形的轴对称图形.
线段的端点,线与线的交点、中点等
如图,把下列图形补成关于直线 l 对称的轴对称图形.
l
l
作轴对称图形的口诀:作垂线,截等线,顺次连.
典例精析
画轴对称图形
轴对称变换
轴对称变换的性质
画出已知图形的轴对称图形
成轴对称的两个图形全等
1.新旧图形的对应点是对称点;
2.连接对应点的线段被对称轴垂直平分
一找,二画,三连
归纳新知
1.下列说法正确的是( )
A.全等的两个图形是由其中一个经过轴对称变换得到的
B.轴对称变换得到的图形与原图形全等
C.轴对称变换中的两个图形,每一对对应点所连线段都被这两个图形之间的直线垂直平分
D.轴对称变换得到的图形也可以由原图形经过平移得到
B
课后练习
2.如图,△AOD关于直线l进行轴对称变换后得到△BOC,则以下结论中不正确的是( )
A.∠1=∠2
B.∠3=∠4
C.l垂直平分AB,且l垂直平分CD
D.AC与BD互相平分
D
3.如图所示是一只停泊在平静水面上的小船,它的“倒影”应是( )
B
4.下列图形中,分别以直线l为对称轴作轴对称,其中错误的是( )
C
5.下面是四名同学作△ABC关于直线MN的轴对称图形,其中正确的是( )
B
6.如图,在由4个小正方形组成的田字格中,△ABC的顶点都是小正方形的顶点,在田字格上画与△ABC成轴对称的三角形,且顶点都是小正方形的顶点,则这样的三角形(不包含△ABC本身)共有( )
A.1个 B.3个 C.2个 D.4个
B
7.如图,正三角形网格中,已有两个小三角形被涂黑.
(1)再将图①中其余小三角形涂黑一个,使整个被涂黑的图案构成一个轴对称图形(画出两种不同的);
解:如图①所示.
(2)再将图②中其余小三角形涂黑两个,使整个被涂黑的图案构成一个轴对称图形(画出两种不同的).
解:如图②所示.
(答案不唯一.)
8.【2020·吉林】图①、图②、图③都是3×3的正方形网格,每个小正方形的顶点称为格点.A,B,C均为格点,在给定的网格中,按下列要求画图:
(1)在图①中,画一条不与AB重合的线段MN,使MN与AB关于某条直线对称,且M,N为格点;
解:如图①,MN即为所求.(答案不唯一)
(2)在图②中,画一条不与AC重合的线段PQ,使PQ与AC关于某条直线对称,且P,Q为格点;
解:如图②,PQ
即为所求.(答案不唯一)
(3)在图③中,画一个△DEF,使△DEF与△ABC关于某条直线对称,且D,E,F为格点.
解:如图③,△DEF即为所求.(答案不唯一)
再 见
