23.3方差-同步练习-2021-2022学年九年级数学上册冀教版(Word版 含答案)
文档属性
| 名称 | 23.3方差-同步练习-2021-2022学年九年级数学上册冀教版(Word版 含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 223.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-28 10:41:18 | ||
图片预览




文档简介
2021-2022学年九年级数学上册(冀教版)
23.3方差-同步练习
时间:60分钟
一、单选题
1.样本方差的计算公式S2=[(-30)2+(-30)]2+…+(-30)2]中,数字20和30分别表示样本中的( )
A.众数、中位数 B.方差、标准差
C.样本中数据的个数、平均数 D.样本中数据的个数、中位数
2.在某次射击训练中,甲、乙、丙、丁四位选手各10次射击成绩的平均数和方差如下表:
选手 甲 乙 丙 丁
平均数 9.2 9.2 9.2 9.2
方差 0.35 0.27 0.25 0.15
则这四人中,成绩波动最大的是( )
A.甲 B.乙 C.丙 D.丁
3.如果数据的平均数是9,方差为3,那么数据的平均数、方差分别是( )
A.9,3 B.9,4 C.10,3 D.10,4
4.在一次“我的青春,我的梦”演讲比赛中,五名选手的成绩及部分统计信息如下表,其中被遮住的两个数据依次是( )
组员及项目 甲 乙 丙 丁 戊 方差 平均分
得分 91 89 90 92 90
A.88, B.88,2 C.90, D.90,2
5.一组数据的方差为S2,将该数据每一个数据,都乘以2,所得到的一组新数据的方差是( )
A. B.S2 C.2 S2 D.4 S2
6.下列统计量中,能反映一名同学在7~9年级学段的学习成绩稳定程度的是( )
A.平均数 B.中位数 C.众数 D.方差
7.小莹同学10个周综合素质评价成绩统计如下:
成绩(分) 94 95 97 98 100
周数(个) 1 2 2 4 1
这10个周的综合素质评价成绩的中位数和方差分别是( )
A.97.5 2.8 B.97.5 3
C.97 2.8 D.97 3
8.现在要选拔一人去参加全国青少年数学竞赛,小明和小刚的三次选拔成绩分别为:小明:96,85,89,小刚:90,91,89,最终决定选择小刚去参加,那么,最终依据是( )
A.小刚的平均分高 B.小刚的中位数高 C.小刚的方差小 D.小刚最低分高
二、填空题
9.甲、乙两地9月上旬的日平均气温如图所示,则甲、乙两地这10天日平均气温方差大小关系为s甲2__________s乙2(填“>”或“<”).
10.甲、乙两人5次射击命中的环数如下:
甲:7,9,8,6,10
乙:7,8,9 ,8, 8
则这两人5次射击命中的环数的平均数==8,方差_____.(填“>”、“<”或“=”)
11.如果样本方差s2=[(x1-2)2+(x2-2)2+(x3-2)2+(x4-2)2],那么这个样本的平均数为__________,样本容量为________.
12.某公司两名业务主管5个月的工作业绩考核得分如下:
甲:5、6、8、7、9;
乙:3、6、7、9、10.
则_______的工作业绩较稳定.〔选填“甲”或“乙”)
13.随机从甲、乙两块试验田中各抽取株麦苗测量高度,计算平均数和方差的结果:,,,,则小麦长势比较整齐的试验田是_____________.
14.五个数1,2,4,5,a的平均数是3,则a=____,这五个数的方差为_________.
15.某校准备从甲、乙、丙、丁四个科创小组中选出一组,参加区青少年科技创新大赛,表格反映的是各组平时成绩的平均数(单位:分)及方差S2,如果要选出一个成绩较好且状态稳定的组去参赛,那么应选的组是_____.
甲 乙 丙 丁
7 8 8 7
s2 1 1.2 0.9 1.8
16.某工程队有14名员工,他们的工种及相应每人每月工资如下表所示:
现该工程队进行了人员调整:减少木工2名,增加电工、瓦工各1名,与调整前相比,该工程队员工月工资的方差_______(填“变小”、“不变”或“变大”).
三、解答题
17.小芳测得连续五天的最低气温并整理后的出下表
日期 一 二 三 四 五 方差 平均气温
最低气温 1 3 2 5 3
由于不小心被墨迹污染了两个数据,这两个数据分别是什么?
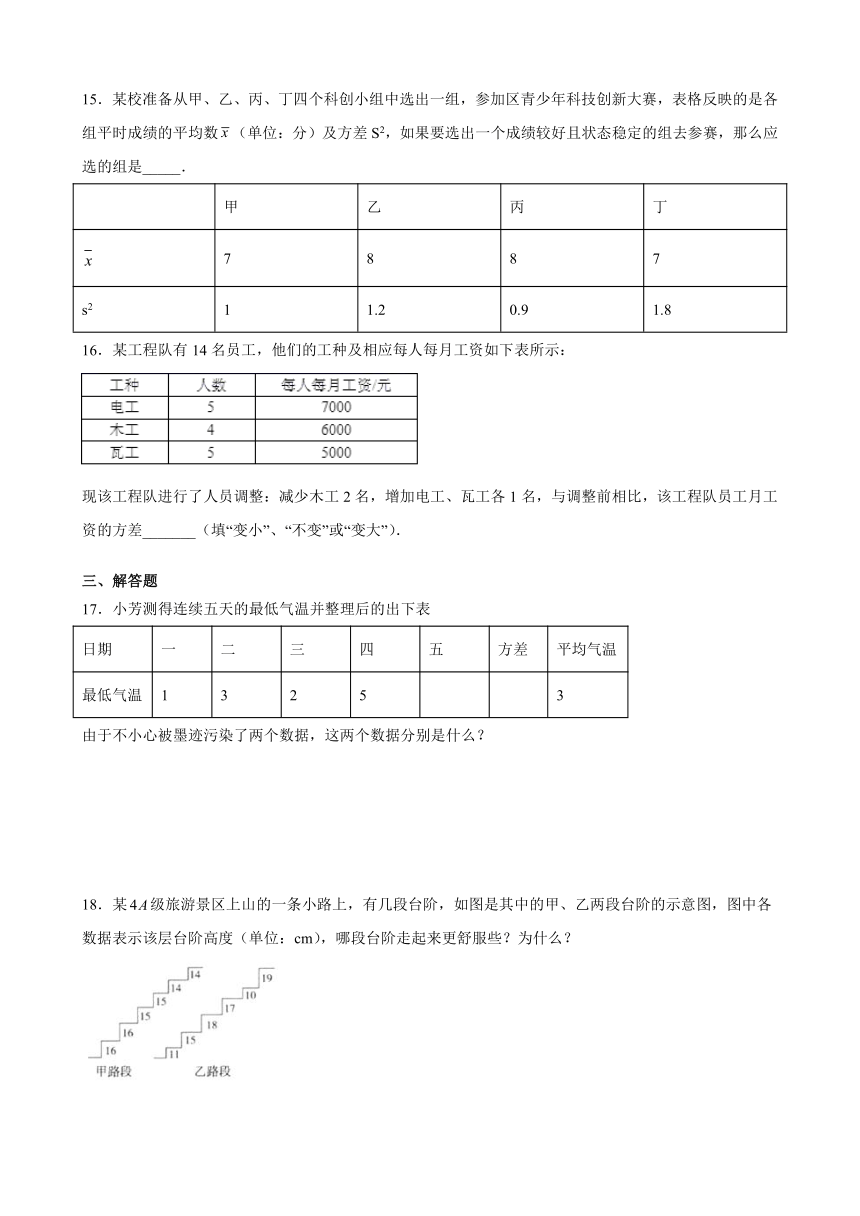
18.某级旅游景区上山的一条小路上,有几段台阶,如图是其中的甲、乙两段台阶的示意图,图中各数据表示该层台阶高度(单位:cm),哪段台阶走起来更舒服些?为什么?
19.已知学习小组5位同学参加学业水平测试(满分100分)的平均成绩是80分,其中两位女生的成绩分别为85分,75分,三位男生成绩的方差为150(分).
(1)学习小组三位男生成绩的平均数是_______分;
(2)求学习小组5位同学成绩的方差.
20.甲、乙两台包装机同时包装的糖果,从中各抽出10袋,测得实际质量(g)
如下:
甲:501 505 508 508 494 508 506 508 507 499
乙:508 507 505 498 507 506 508 507 507 506
(1)分别计算两组数据的平均数(结果四舍五入保留整数)和方差;
(2)哪台包装机包装糖果的质量比较稳定?
21.甲乙两名战士在相同条件下各射击10次,每次命中的环数分别是:
甲:8,6,7,8,6,5,9,10,4,7 乙:6,7,7,6,7,8,7,9,8,5
(1)分别求出两组数据的方差和标准差;
(2)根据计算结果,评价一下两名战士的射击情况.
22.浙师大整州外国语学校八年级某班组织了一次经典诵读比赛,甲乙两队各10人的比赛成绩如下表(10分制):
甲 7 8 9 7 10 10 9 10 10 10
乙 10 8 7 9 8 10 10 9 10 9
(1)甲队成绩的中位数是__________分,乙队成绩的众数是_________分;
(2)计算乙队的平均成绩和方差;
(3)已知甲队成绩的方差是1.4分,则成绩较为整齐的是___________队.
23.某校拟派一名跳高运动员参加一项校际比赛,对甲、乙两名跳高运动员进行了8次选拔赛,他们的跳高成绩(单位:)如下:
甲:172 168 175 169 174 167 166 169
乙:164 175 174 165 162 173 172 175
(1)甲、乙两名运动员跳高的平均成绩分别是多少?
(2)分别求出甲、乙跳高成绩的方差;
(3)哪个人的成绩更为稳定?为什么?
(4)经预测,跳高以上就很可能获得冠军,该校为了获取跳高比赛冠军,可能选哪位运动员参赛?若预测跳高方可获得冠军,又应该选哪位运动员参赛?
试卷第2页,共2页
参考答案
1.C
【解析】解:∵S2=[(-30)2+(-30)]2+…+(-30)2]
∴20是样本中数据的个数,30是这组数据的平均数.
故选C.
2.A
【解析】解:由表知,,
∴甲的方差最大,
∴这四人中,成绩波动最大的是甲.
故选:A.
3.C
【解析】解:∵数据的平均数是9,方差为3,
∴的平均数为,方差不变,为3.
故选:C.
4.B
【解析】解:根据题意得:
(分),
则丙的得分是88分;
方差为.
故选:B.
5.D
【解析】解:将该数据每一个数据都乘以2,即每个数据都扩大2倍,根据一组数据扩大n倍后,方差是原数据方差的n2倍,即S2×22=4 S2.
故选D.
6.D
【解析】由于方差反映数据的波动大小,则能反映学生的成绩稳定程度的是方差.
故选D.
7.B
【解析】这10个周的综合素质评价成绩的中位数是(分),
平均成绩为(分),
∴这组数据的方差为,
故选B.
8.C
【解析】解:A.平均数:小明的平均数=,小刚的平均数=,平均数相同,故此项错误;
B.中位数:小明的中位数89,小刚的中位数90,89<90,但中位数不能代表平均水平,故此项错误;
C.方差:小明的方差=,小刚的方差=,>,小刚的波动较小,故小刚的方差较小,故此项正确;
D. 此时不能选择最低分来比较两人的水平,故此项错误.
故选C.
9.>
【解析】解:由气温统计图可知:乙地的气温波动小,比较稳定
∴乙地气温的方差小
∴
故答案为:>.
10.>
【解析】解:S2甲=[(7-8)2+(9 8)2+(8 8)2+(6 8)2+(10 8)2)]=2,
S2乙=[(7-8)2+(8 8)2+(9 8)2+(8 8)2+(8 8)2)]=0.4,
∴S2甲>S2乙.
故答案为:>.
11.2 4
【解析】解:根据方差公式可得这个样本的平均数为2,样本容量为4.
12.甲
【解析】甲的平均业绩为:,乙的平均业绩为:,∴甲业绩的方差为:,乙业绩的方差为:,,
∴甲的工作业绩更稳定.
故答案为:甲.
13.甲
【解析】解:由方差的意义,观察数据可知,
∵,
∴甲块试验田的方差小,
故甲试验田小麦长势比较整齐.
故答案为:甲.
14.3 2
【解析】由题意知:a=15﹣(1+2+4+5)=3,这五个数的方差S2=[(1﹣3)2+(2﹣3)2+(4﹣3)2+(5﹣3)2+(3﹣3)2]=2.
故答案为3;2.
15.丙
【解析】因为乙组、丙组的平均数比甲组、丁组大,而丙组的方差比乙组的小,
所以丙组的成绩比较稳定,
所以丙组的成绩较好且状态稳定,应选的组是丙组.
故答案为丙.
16.变大.
【解析】∵减少木工2名,增加电工、瓦工各1名,∴这组数据的平均数不变,但是每个数据减去平均数后平方和增大,则该工程队员工月工资的方差变大.故答案为变大.
17.4,2
【解析】解:3×5-(1+3+2+5)=4
18.甲路段台阶走起来更舒服些,见解析.
【解析】,
.
甲组数据的极差为,
乙组数据的极差为.
,
由于甲路段台阶高度的极差、方差均小于乙路段的极差和方差,因此,甲路段台阶高度起伏较小,走起来更舒服些.
19.(1)80;(2)100
【解析】解:(1)的平均数是,
故答案为:80;
(2)三名男生的成绩为,则其方差,
∴,
∴5位同学成绩的方差为:.
20.(1),,,,(2)乙包装机包装糖果的质量比较稳定.
【解析】(1),
,
.
,
(2),
乙包装机包装糖果的质量比较稳定.
21.(1),;,;(2)平均水平相同,乙射击较稳定
【解析】解(1)∵ =×(8+6+7+8+6+5+9+10+4+7)=7,
∴=×[(8 7)2+(6 7)2+(7 7)2+(8 7)2+(6-7)2+(5 7)2+(9 7)2+(10 7)2+(4 7)2+(7 7)2],
=×(1+1+0+1+1+4+4+9+9+0),
=3,
∴;
∵=×(6+7+7+6+7+8+7+9+8+5)=7,
∴=×[(6 7)2+(7 7)2+(7 7)2+(6 7)2+(7-7)2+(8 7)2+(7 7)2+(9 7)2+(8 7)2+(5 7)2],
=×(1+0+0+1+0+1+0+4+1+4),
=,
∴;
(2)∵= ,<,
∴甲乙两人平均成绩一样,乙射击成绩的方差小于甲,即可得出乙的成绩更加稳定.
22.(1)9.5,10;(2)9分,1;(3)乙
【解析】解:(1)把甲队的成绩从小到大排列为:7,7,8,9,9,10,10,10,10,10,最中间两个数的平均数是(分),
则中位数是9.5分;
乙队成绩中10出现了4次,出现的次数最多,
则乙队成绩的众数是10分;
故答案为:9.5,10;
(2)乙队的平均成绩是:,
则乙队的方差是:;
(3)甲队成绩的方差是1.4分,乙队的方差是1,甲队成绩的方差乙队的方差,
乙队较为整齐.
23.(1)都是170cm;(2),;(3)甲运动员的成绩更为稳定,理由见解析;(4)跳高以上就很可能获得冠军的情况下,选甲运动员参加;跳高方可获得冠军的情况下,应选乙运动员参加
【解析】(1)甲的平均成绩为:,
乙的平均成绩为:,
(2)
;
(3)∵,
∴,
∴甲运动员的成绩更为稳定;
(4)若跳过以上就很可能获得冠军,则在8次成绩中,甲8次都跳过了,而乙只有5次,所以应选甲运动员参加;若跳过才能得冠军,则在8次成绩中,甲只有3次都跳过了,而乙有5次,所以应选乙运动员参加.
答案第1页,共2页
答案第1页,共2页
23.3方差-同步练习
时间:60分钟
一、单选题
1.样本方差的计算公式S2=[(-30)2+(-30)]2+…+(-30)2]中,数字20和30分别表示样本中的( )
A.众数、中位数 B.方差、标准差
C.样本中数据的个数、平均数 D.样本中数据的个数、中位数
2.在某次射击训练中,甲、乙、丙、丁四位选手各10次射击成绩的平均数和方差如下表:
选手 甲 乙 丙 丁
平均数 9.2 9.2 9.2 9.2
方差 0.35 0.27 0.25 0.15
则这四人中,成绩波动最大的是( )
A.甲 B.乙 C.丙 D.丁
3.如果数据的平均数是9,方差为3,那么数据的平均数、方差分别是( )
A.9,3 B.9,4 C.10,3 D.10,4
4.在一次“我的青春,我的梦”演讲比赛中,五名选手的成绩及部分统计信息如下表,其中被遮住的两个数据依次是( )
组员及项目 甲 乙 丙 丁 戊 方差 平均分
得分 91 89 90 92 90
A.88, B.88,2 C.90, D.90,2
5.一组数据的方差为S2,将该数据每一个数据,都乘以2,所得到的一组新数据的方差是( )
A. B.S2 C.2 S2 D.4 S2
6.下列统计量中,能反映一名同学在7~9年级学段的学习成绩稳定程度的是( )
A.平均数 B.中位数 C.众数 D.方差
7.小莹同学10个周综合素质评价成绩统计如下:
成绩(分) 94 95 97 98 100
周数(个) 1 2 2 4 1
这10个周的综合素质评价成绩的中位数和方差分别是( )
A.97.5 2.8 B.97.5 3
C.97 2.8 D.97 3
8.现在要选拔一人去参加全国青少年数学竞赛,小明和小刚的三次选拔成绩分别为:小明:96,85,89,小刚:90,91,89,最终决定选择小刚去参加,那么,最终依据是( )
A.小刚的平均分高 B.小刚的中位数高 C.小刚的方差小 D.小刚最低分高
二、填空题
9.甲、乙两地9月上旬的日平均气温如图所示,则甲、乙两地这10天日平均气温方差大小关系为s甲2__________s乙2(填“>”或“<”).
10.甲、乙两人5次射击命中的环数如下:
甲:7,9,8,6,10
乙:7,8,9 ,8, 8
则这两人5次射击命中的环数的平均数==8,方差_____.(填“>”、“<”或“=”)
11.如果样本方差s2=[(x1-2)2+(x2-2)2+(x3-2)2+(x4-2)2],那么这个样本的平均数为__________,样本容量为________.
12.某公司两名业务主管5个月的工作业绩考核得分如下:
甲:5、6、8、7、9;
乙:3、6、7、9、10.
则_______的工作业绩较稳定.〔选填“甲”或“乙”)
13.随机从甲、乙两块试验田中各抽取株麦苗测量高度,计算平均数和方差的结果:,,,,则小麦长势比较整齐的试验田是_____________.
14.五个数1,2,4,5,a的平均数是3,则a=____,这五个数的方差为_________.
15.某校准备从甲、乙、丙、丁四个科创小组中选出一组,参加区青少年科技创新大赛,表格反映的是各组平时成绩的平均数(单位:分)及方差S2,如果要选出一个成绩较好且状态稳定的组去参赛,那么应选的组是_____.
甲 乙 丙 丁
7 8 8 7
s2 1 1.2 0.9 1.8
16.某工程队有14名员工,他们的工种及相应每人每月工资如下表所示:
现该工程队进行了人员调整:减少木工2名,增加电工、瓦工各1名,与调整前相比,该工程队员工月工资的方差_______(填“变小”、“不变”或“变大”).
三、解答题
17.小芳测得连续五天的最低气温并整理后的出下表
日期 一 二 三 四 五 方差 平均气温
最低气温 1 3 2 5 3
由于不小心被墨迹污染了两个数据,这两个数据分别是什么?
18.某级旅游景区上山的一条小路上,有几段台阶,如图是其中的甲、乙两段台阶的示意图,图中各数据表示该层台阶高度(单位:cm),哪段台阶走起来更舒服些?为什么?
19.已知学习小组5位同学参加学业水平测试(满分100分)的平均成绩是80分,其中两位女生的成绩分别为85分,75分,三位男生成绩的方差为150(分).
(1)学习小组三位男生成绩的平均数是_______分;
(2)求学习小组5位同学成绩的方差.
20.甲、乙两台包装机同时包装的糖果,从中各抽出10袋,测得实际质量(g)
如下:
甲:501 505 508 508 494 508 506 508 507 499
乙:508 507 505 498 507 506 508 507 507 506
(1)分别计算两组数据的平均数(结果四舍五入保留整数)和方差;
(2)哪台包装机包装糖果的质量比较稳定?
21.甲乙两名战士在相同条件下各射击10次,每次命中的环数分别是:
甲:8,6,7,8,6,5,9,10,4,7 乙:6,7,7,6,7,8,7,9,8,5
(1)分别求出两组数据的方差和标准差;
(2)根据计算结果,评价一下两名战士的射击情况.
22.浙师大整州外国语学校八年级某班组织了一次经典诵读比赛,甲乙两队各10人的比赛成绩如下表(10分制):
甲 7 8 9 7 10 10 9 10 10 10
乙 10 8 7 9 8 10 10 9 10 9
(1)甲队成绩的中位数是__________分,乙队成绩的众数是_________分;
(2)计算乙队的平均成绩和方差;
(3)已知甲队成绩的方差是1.4分,则成绩较为整齐的是___________队.
23.某校拟派一名跳高运动员参加一项校际比赛,对甲、乙两名跳高运动员进行了8次选拔赛,他们的跳高成绩(单位:)如下:
甲:172 168 175 169 174 167 166 169
乙:164 175 174 165 162 173 172 175
(1)甲、乙两名运动员跳高的平均成绩分别是多少?
(2)分别求出甲、乙跳高成绩的方差;
(3)哪个人的成绩更为稳定?为什么?
(4)经预测,跳高以上就很可能获得冠军,该校为了获取跳高比赛冠军,可能选哪位运动员参赛?若预测跳高方可获得冠军,又应该选哪位运动员参赛?
试卷第2页,共2页
参考答案
1.C
【解析】解:∵S2=[(-30)2+(-30)]2+…+(-30)2]
∴20是样本中数据的个数,30是这组数据的平均数.
故选C.
2.A
【解析】解:由表知,,
∴甲的方差最大,
∴这四人中,成绩波动最大的是甲.
故选:A.
3.C
【解析】解:∵数据的平均数是9,方差为3,
∴的平均数为,方差不变,为3.
故选:C.
4.B
【解析】解:根据题意得:
(分),
则丙的得分是88分;
方差为.
故选:B.
5.D
【解析】解:将该数据每一个数据都乘以2,即每个数据都扩大2倍,根据一组数据扩大n倍后,方差是原数据方差的n2倍,即S2×22=4 S2.
故选D.
6.D
【解析】由于方差反映数据的波动大小,则能反映学生的成绩稳定程度的是方差.
故选D.
7.B
【解析】这10个周的综合素质评价成绩的中位数是(分),
平均成绩为(分),
∴这组数据的方差为,
故选B.
8.C
【解析】解:A.平均数:小明的平均数=,小刚的平均数=,平均数相同,故此项错误;
B.中位数:小明的中位数89,小刚的中位数90,89<90,但中位数不能代表平均水平,故此项错误;
C.方差:小明的方差=,小刚的方差=,>,小刚的波动较小,故小刚的方差较小,故此项正确;
D. 此时不能选择最低分来比较两人的水平,故此项错误.
故选C.
9.>
【解析】解:由气温统计图可知:乙地的气温波动小,比较稳定
∴乙地气温的方差小
∴
故答案为:>.
10.>
【解析】解:S2甲=[(7-8)2+(9 8)2+(8 8)2+(6 8)2+(10 8)2)]=2,
S2乙=[(7-8)2+(8 8)2+(9 8)2+(8 8)2+(8 8)2)]=0.4,
∴S2甲>S2乙.
故答案为:>.
11.2 4
【解析】解:根据方差公式可得这个样本的平均数为2,样本容量为4.
12.甲
【解析】甲的平均业绩为:,乙的平均业绩为:,∴甲业绩的方差为:,乙业绩的方差为:,,
∴甲的工作业绩更稳定.
故答案为:甲.
13.甲
【解析】解:由方差的意义,观察数据可知,
∵,
∴甲块试验田的方差小,
故甲试验田小麦长势比较整齐.
故答案为:甲.
14.3 2
【解析】由题意知:a=15﹣(1+2+4+5)=3,这五个数的方差S2=[(1﹣3)2+(2﹣3)2+(4﹣3)2+(5﹣3)2+(3﹣3)2]=2.
故答案为3;2.
15.丙
【解析】因为乙组、丙组的平均数比甲组、丁组大,而丙组的方差比乙组的小,
所以丙组的成绩比较稳定,
所以丙组的成绩较好且状态稳定,应选的组是丙组.
故答案为丙.
16.变大.
【解析】∵减少木工2名,增加电工、瓦工各1名,∴这组数据的平均数不变,但是每个数据减去平均数后平方和增大,则该工程队员工月工资的方差变大.故答案为变大.
17.4,2
【解析】解:3×5-(1+3+2+5)=4
18.甲路段台阶走起来更舒服些,见解析.
【解析】,
.
甲组数据的极差为,
乙组数据的极差为.
,
由于甲路段台阶高度的极差、方差均小于乙路段的极差和方差,因此,甲路段台阶高度起伏较小,走起来更舒服些.
19.(1)80;(2)100
【解析】解:(1)的平均数是,
故答案为:80;
(2)三名男生的成绩为,则其方差,
∴,
∴5位同学成绩的方差为:.
20.(1),,,,(2)乙包装机包装糖果的质量比较稳定.
【解析】(1),
,
.
,
(2),
乙包装机包装糖果的质量比较稳定.
21.(1),;,;(2)平均水平相同,乙射击较稳定
【解析】解(1)∵ =×(8+6+7+8+6+5+9+10+4+7)=7,
∴=×[(8 7)2+(6 7)2+(7 7)2+(8 7)2+(6-7)2+(5 7)2+(9 7)2+(10 7)2+(4 7)2+(7 7)2],
=×(1+1+0+1+1+4+4+9+9+0),
=3,
∴;
∵=×(6+7+7+6+7+8+7+9+8+5)=7,
∴=×[(6 7)2+(7 7)2+(7 7)2+(6 7)2+(7-7)2+(8 7)2+(7 7)2+(9 7)2+(8 7)2+(5 7)2],
=×(1+0+0+1+0+1+0+4+1+4),
=,
∴;
(2)∵= ,<,
∴甲乙两人平均成绩一样,乙射击成绩的方差小于甲,即可得出乙的成绩更加稳定.
22.(1)9.5,10;(2)9分,1;(3)乙
【解析】解:(1)把甲队的成绩从小到大排列为:7,7,8,9,9,10,10,10,10,10,最中间两个数的平均数是(分),
则中位数是9.5分;
乙队成绩中10出现了4次,出现的次数最多,
则乙队成绩的众数是10分;
故答案为:9.5,10;
(2)乙队的平均成绩是:,
则乙队的方差是:;
(3)甲队成绩的方差是1.4分,乙队的方差是1,甲队成绩的方差乙队的方差,
乙队较为整齐.
23.(1)都是170cm;(2),;(3)甲运动员的成绩更为稳定,理由见解析;(4)跳高以上就很可能获得冠军的情况下,选甲运动员参加;跳高方可获得冠军的情况下,应选乙运动员参加
【解析】(1)甲的平均成绩为:,
乙的平均成绩为:,
(2)
;
(3)∵,
∴,
∴甲运动员的成绩更为稳定;
(4)若跳过以上就很可能获得冠军,则在8次成绩中,甲8次都跳过了,而乙只有5次,所以应选甲运动员参加;若跳过才能得冠军,则在8次成绩中,甲只有3次都跳过了,而乙有5次,所以应选乙运动员参加.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
