3.4二次函数y=ax2 bx c的图象与性质 同步练习题 2021-2022学年鲁教版(五四制)九年级数学上册(Word版 含答案)
文档属性
| 名称 | 3.4二次函数y=ax2 bx c的图象与性质 同步练习题 2021-2022学年鲁教版(五四制)九年级数学上册(Word版 含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 312.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-28 10:45:12 | ||
图片预览


文档简介
2021-2022学年鲁教版九年级数学上册《3.4二次函数y=ax2+bx+c的图象与性质》
同步练习题(附答案)
一.选择题
1.把抛物线y=x2+1向左平移1个单位,则平移后抛物线的解析式为( )
A.y=(x+1)2+1 B.y=(x﹣1)2+1 C.y=x2+2 D.y=x2
2.点P1(﹣2,y1),P2(2,y2),P3(4,y3)均在二次函数y=﹣x2+2x+c的图象上,则y1,y2,y3的大小关系是( )
A.y2>y3>y1 B.y2>y1=y3 C.y1=y3>y2 D.y1=y2>y3
3.若函数y=x2﹣4x+m的图象上有两点A(x1,y1),B(x2,y2),若x1<x2<2,则( )
A.y1>y2 B.y1<y2
C.y1=y2 D.y1,y2的大小不确定
4.如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴为x=且经过点(2,0).下列说法:①abc<0;②4a+2b+c<0;③﹣2b+c=0;④若(﹣,y1),(,y2)是抛物线上的两点,则y1<y2;⑤b>m(am+b)(其中m≠).其中说法正确的是( )
①③④⑤ B.①②④
C.①④⑤ D.③④⑤
5.二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①abc>0,②2a+b=0,③b<a+c,④3a+c=0,其中错误的结论有( )
A.1个 B.2个 C.3个 D.4个
6.二次函数y=ax2+bx+c的部分图象如图,图象过点A(3,0),对称轴为直线x=1,下列结论:①a﹣b+c=0;②2a+b=0; ③4ac﹣b2>0;④a+b≥am2+bm(m为实数);⑤3a+c>0.则其中正确的结论有( )
A.2个 B.3个 C.4个 D.5个
7.已知抛物线y=ax2+bx+m是由抛物线y=﹣x2+2x+2先关于y轴作轴对称图形,再将所得的图象向下平移3个单位长度得到的,点Q1(﹣2.5,q1)、Q2(1,q2)都在抛物线y=ax2+bx+m上,则q1,q2的大小关系是( )
A.q1>q2 B.q1=q2 C.q1<q2 D.不能确定
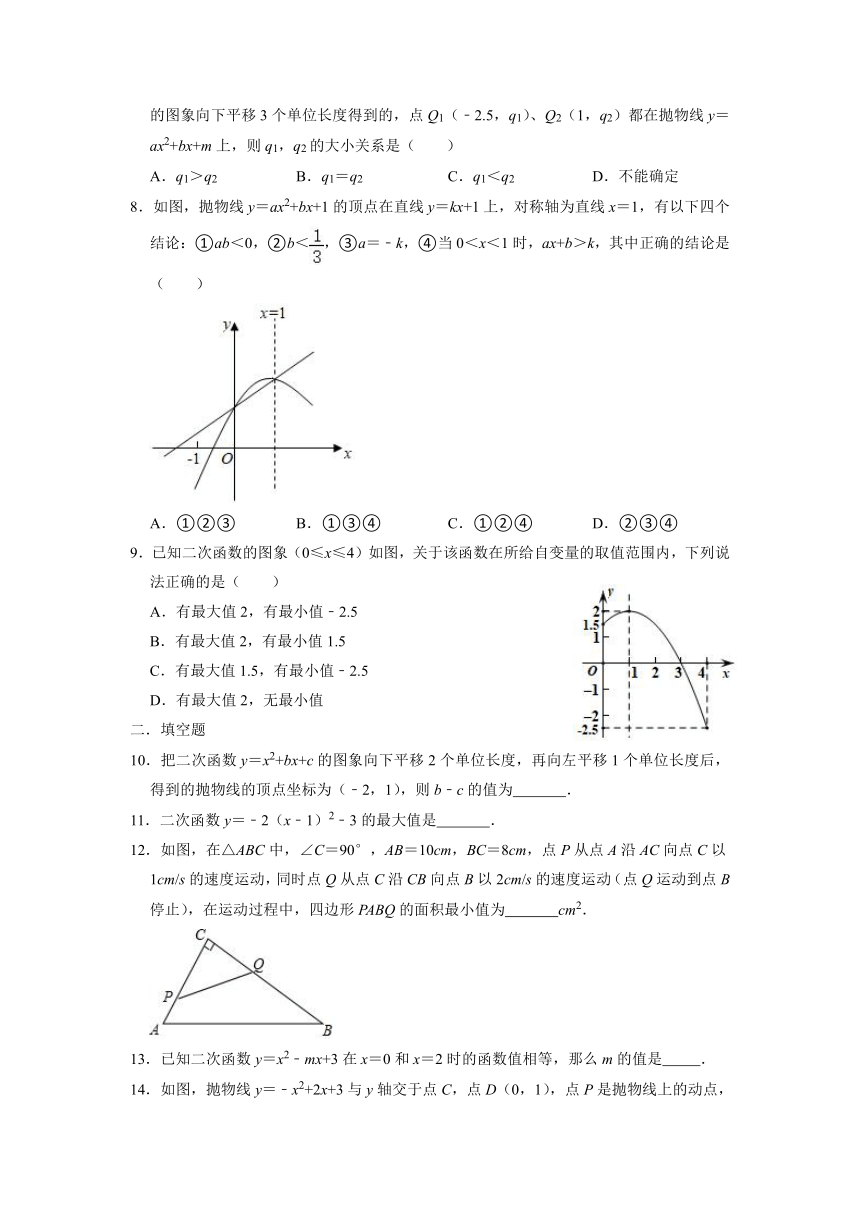
8.如图,抛物线y=ax2+bx+1的顶点在直线y=kx+1上,对称轴为直线x=1,有以下四个结论:①ab<0,②b<,③a=﹣k,④当0<x<1时,ax+b>k,其中正确的结论是( )
A.①②③ B.①③④ C.①②④ D.②③④
9.已知二次函数的图象(0≤x≤4)如图,关于该函数在所给自变量的取值范围内,下列说法正确的是( )
A.有最大值2,有最小值﹣2.5
B.有最大值2,有最小值1.5
C.有最大值1.5,有最小值﹣2.5
D.有最大值2,无最小值
二.填空题
10.把二次函数y=x2+bx+c的图象向下平移2个单位长度,再向左平移1个单位长度后,得到的抛物线的顶点坐标为(﹣2,1),则b﹣c的值为 .
11.二次函数y=﹣2(x﹣1)2﹣3的最大值是 .
12.如图,在△ABC中,∠C=90°,AB=10cm,BC=8cm,点P从点A沿AC向点C以1cm/s的速度运动,同时点Q从点C沿CB向点B以2cm/s的速度运动(点Q运动到点B停止),在运动过程中,四边形PABQ的面积最小值为 cm2.
13.已知二次函数y=x2﹣mx+3在x=0和x=2时的函数值相等,那么m的值是 .
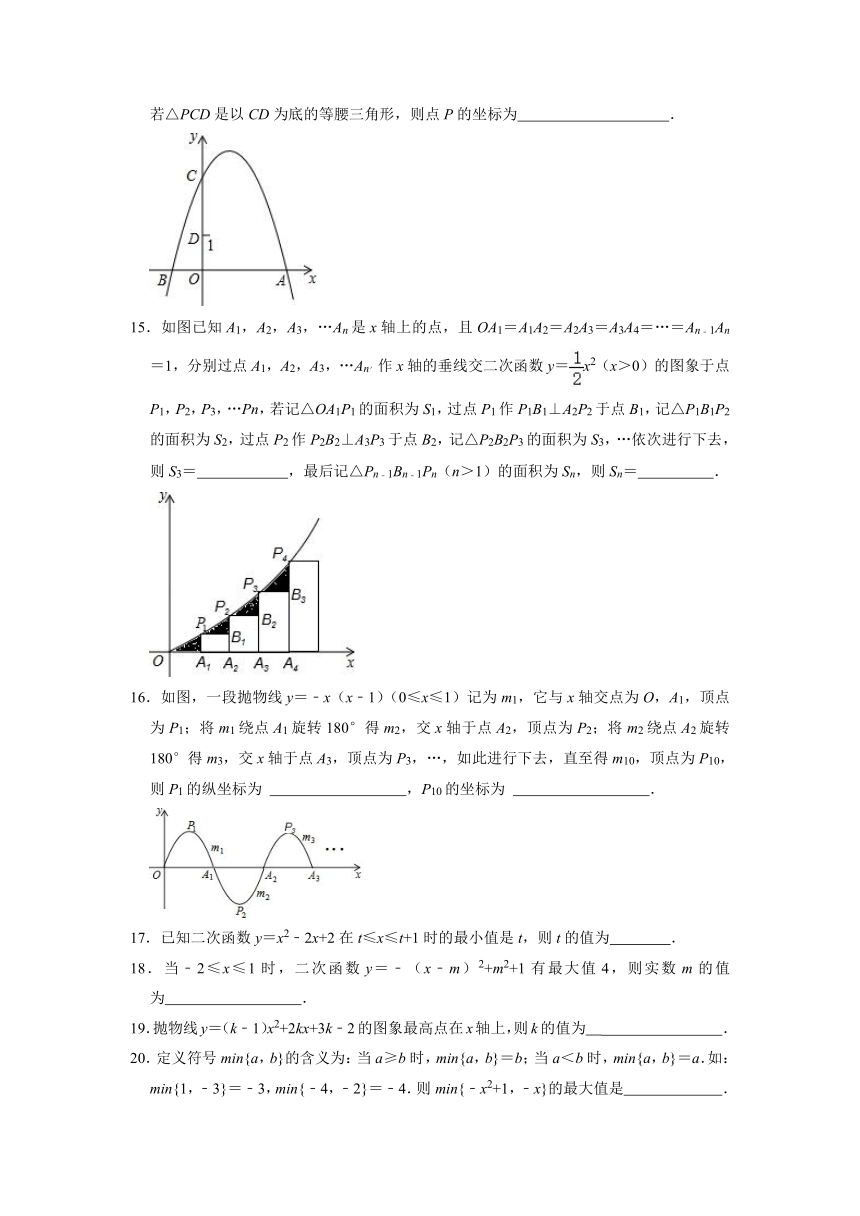
14.如图,抛物线y=﹣x2+2x+3与y轴交于点C,点D(0,1),点P是抛物线上的动点,若△PCD是以CD为底的等腰三角形,则点P的坐标为 .
15.如图已知A1,A2,A3,…An是x轴上的点,且OA1=A1A2=A2A3=A3A4=…=An﹣1An=1,分别过点A1,A2,A3,…An′作x轴的垂线交二次函数y=x2(x>0)的图象于点P1,P2,P3,…Pn,若记△OA1P1的面积为S1,过点P1作P1B1⊥A2P2于点B1,记△P1B1P2的面积为S2,过点P2作P2B2⊥A3P3于点B2,记△P2B2P3的面积为S3,…依次进行下去,则S3= ,最后记△Pn﹣1Bn﹣1Pn(n>1)的面积为Sn,则Sn= .
16.如图,一段抛物线y=﹣x(x﹣1)(0≤x≤1)记为m1,它与x轴交点为O,A1,顶点为P1;将m1绕点A1旋转180°得m2,交x轴于点A2,顶点为P2;将m2绕点A2旋转180°得m3,交x轴于点A3,顶点为P3,…,如此进行下去,直至得m10,顶点为P10,则P1的纵坐标为 ,P10的坐标为 .
17.已知二次函数y=x2﹣2x+2在t≤x≤t+1时的最小值是t,则t的值为 .
18.当﹣2≤x≤1时,二次函数y=﹣(x﹣m)2+m2+1有最大值4,则实数m的值为 .
19.抛物线y=(k﹣1)x2+2kx+3k﹣2的图象最高点在x轴上,则k的值为 .
20.定义符号min{a,b}的含义为:当a≥b时,min{a,b}=b;当a<b时,min{a,b}=a.如:min{1,﹣3}=﹣3,min{﹣4,﹣2}=﹣4.则min{﹣x2+1,﹣x}的最大值是 .
21.二次函数y=x2+2ax+a在﹣1≤x≤2上有最小值﹣4,则a的值为 .
三.解答题
22.如图,矩形ABCD的两边长AB=16cm,AD=4cm,点P,Q分别从A,B同时出发,P在边AB上沿AB方向以每秒2cm的速度匀速运动,Q在边BC上沿BC方向以每秒1cm的速度匀速运动设运动时间为x(秒),设△BPQ的面积为ycm2.
(1)求y关于x的函数关系式,并写出x的取值范围;
(2)当△BPQ面积有最大值时,求x的值.
23.如图,在矩形ABCD中,AB=6cm,BC=8cm,点P从点A开始沿边AB向终点B以1cm/s的速度移动,与此同时,点Q从点B开始沿边BC向终点C以2cm/s的速度移动.如果P,Q分别从A,B同时出发,当点Q运动到点C时,两点停止运动,设运动时间为t秒.
(1)填空:BQ= ,PB= ;(用含t的代数式表示)
(2)当t为何值时,PQ的长度等于3cm?
(3)当t为何值时,五边形APQCD的面积有最小值?最小值为多少?
24.将二次函数y=﹣x2+2x+1的图象
(1)向右平移3个单位,向下平移2个单位得到的函数解析式是 ;
(2)绕它的顶点旋转180°所得抛物线解析式为 ;
(3)绕原点旋转180°所得抛物线解析式为 ;
(4)求沿x轴翻折所得抛物线解析式;
(5)求沿y轴翻折所得抛物线解析式为.
25.对实数a,b,定义运算“*”为:a*b=
(1)求函数y=x*(2x﹣1)的解析式;
(2)若点A(x1,y1)、B(x2,y2)(x1<x2)在函数y=x*(2x﹣1)的图象上,且A、B两点关于坐标原点成中心对称,求点A的坐标;
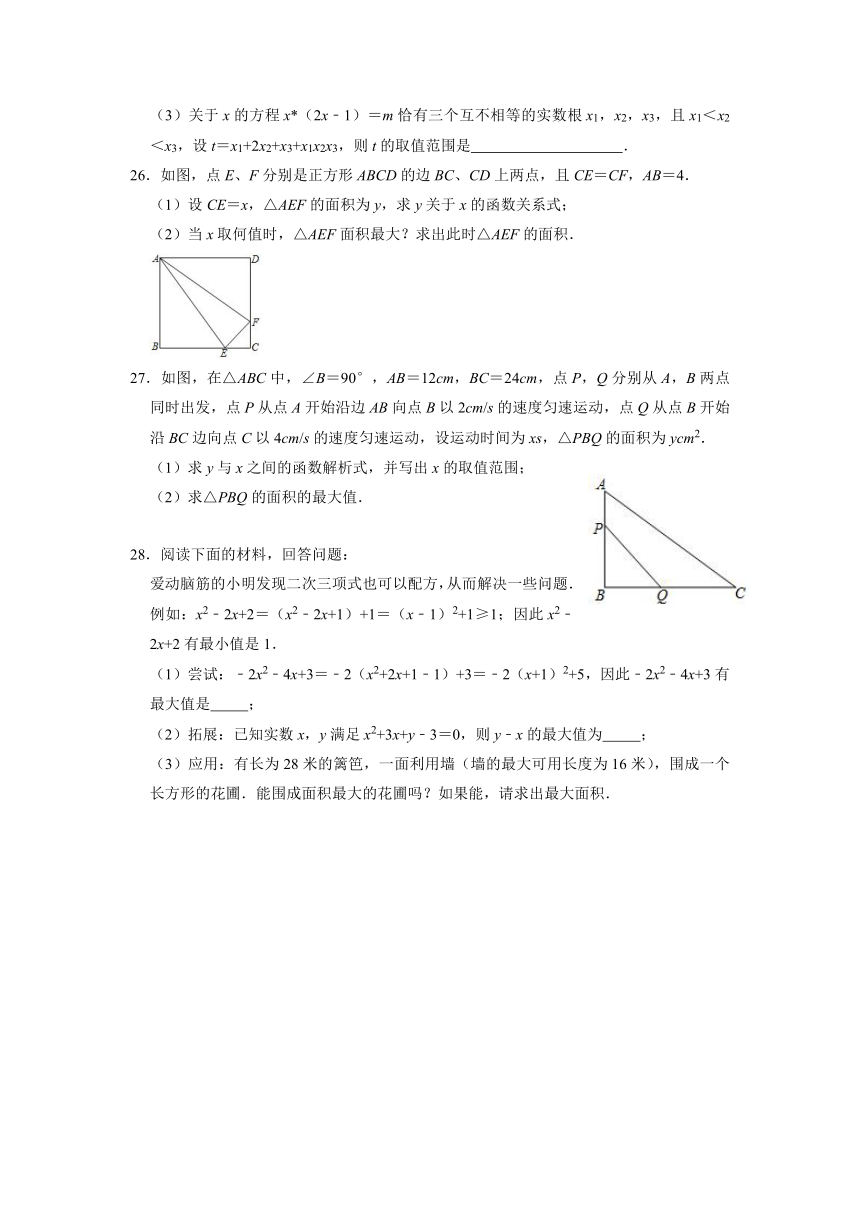
(3)关于x的方程x*(2x﹣1)=m恰有三个互不相等的实数根x1,x2,x3,且x1<x2<x3,设t=x1+2x2+x3+x1x2x3,则t的取值范围是 .
26.如图,点E、F分别是正方形ABCD的边BC、CD上两点,且CE=CF,AB=4.
(1)设CE=x,△AEF的面积为y,求y关于x的函数关系式;
(2)当x取何值时,△AEF面积最大?求出此时△AEF的面积.
27.如图,在△ABC中,∠B=90°,AB=12cm,BC=24cm,点P,Q分别从A,B两点同时出发,点P从点A开始沿边AB向点B以2cm/s的速度匀速运动,点Q从点B开始沿BC边向点C以4cm/s的速度匀速运动,设运动时间为xs,△PBQ的面积为ycm2.
(1)求y与x之间的函数解析式,并写出x的取值范围;
(2)求△PBQ的面积的最大值.
28.阅读下面的材料,回答问题:
爱动脑筋的小明发现二次三项式也可以配方,从而解决一些问题.
例如:x2﹣2x+2=(x2﹣2x+1)+1=(x﹣1)2+1≥1;因此x2﹣2x+2有最小值是1.
(1)尝试:﹣2x2﹣4x+3=﹣2(x2+2x+1﹣1)+3=﹣2(x+1)2+5,因此﹣2x2﹣4x+3有最大值是 ;
(2)拓展:已知实数x,y满足x2+3x+y﹣3=0,则y﹣x的最大值为 ;
(3)应用:有长为28米的篱笆,一面利用墙(墙的最大可用长度为16米),围成一个长方形的花圃.能围成面积最大的花圃吗?如果能,请求出最大面积.
参考答案
1.解:由“左加右减”的原则可知,把抛物线y=x2+1向左平移1个单位,则平移后抛物线的解析式为:y=(x+1)2+1,
故选:A.
2.解:∵y=﹣x2+2x+c=﹣(x﹣1)2+1+c,
∴图象的开口向下,对称轴是直线x=1,
A(﹣2,y1)关于对称轴的对称点为(4,y1),
∵2<4,
∴y2>y1=y3,
故选:B.
3.解:∵y=x2﹣4x+m,
∴此函数的对称轴为:x=﹣=﹣=2,
∵x1<x2<2,两点都在对称轴左侧,a=1>0,
∴对称轴左侧y随x的增大而减小,
∴y1>y2.
故选:A.
4.解:∵抛物线开口向下,
∴a<0,
∵抛物线对称轴为直线x=﹣=,
∴b=﹣a>0,
∵抛物线与y轴的交点在x轴上方,
∴c>0,
∴abc<0,所以①正确;
∵抛物线经过点(2,0),
∴x=2时,y=0,
∴4a+2b+c=0,所以②错误;
∵对称轴为x=,且经过点(2,0),
∴抛物线与x轴的另一个交点为(﹣1,0),
∴=﹣1×2=﹣2,
∴c=﹣2a,
∴﹣2b+c=2a﹣2a=0,所以③正确;
∵点(﹣,y1)离对称轴要比点(,y2)离对称轴要远,
∴y1<y2,所以④正确.
∵抛物线的对称轴为直线x=,
∴当x=时,y有最大值,
∴a+b+c>am2+bm+c(其中m≠),
∴a+b>m(am+b)(其中m≠),
∵a=﹣b,
∴﹣b+b>m(am+b),
∴b>m(am+b),所以⑤正确;
故选:A.
5.解:∵抛物线开口向上,
∴a>0,
∵抛物线的对称轴为直线x=﹣=1,
∴b=﹣2a<0,
∴2a+b=0,
∵抛物线与y轴的交点在x轴下方,
∴c<0,
∴abc>0,所以①②正确;
∴抛物线与x轴的一个交点坐标为(﹣1,0),
∴y=a﹣b+c=0,
∴b=﹣2a,
∴a+c=b,a+2a+c=0,
∴3a+c=0,所以③错误;④正确.
故选:A.
6.解:∵二次函数y=ax2+bx+c的图象过点A(3,0),对称轴为直线x=1,
∴点A(3,0)关于直线x=1对称点为(﹣1,0),
∴当x=﹣1时,y=0,即a﹣b+c=0.故①正确;
∵对称轴为直线x=1,
∴﹣=1,
∴b=﹣2a,
∴2a+b=0,故②正确;
∵抛物线与x轴有两个交点,
∴Δ=b2﹣4ac>0,
∴4ac﹣b2<0,故③错误;
∵当x=1时,函数有最大值,
∴a+b+c≥am2+bm+c,
∴a+b≥am2+bm,故④正确;
∵b=﹣2a,a﹣b+c=0,
∴a+2a+c=0,即3a+c=0,故⑤错误;
综上,正确的有①②④.
故选:B.
7.解:∵y=﹣x2+2x+2=﹣(x﹣1)2+3,
∴顶点为(1,3)
∴抛物线y=﹣x2+2x+2先作关于y轴的轴对称抛物线的顶点为(﹣1,3),再向下平移3个单位长度顶点为(﹣1,0),
∴抛物线y=ax2+bx+m的解析式为y=﹣(x+1)2,
∵点Q1(﹣2.5,q1)、Q2(1,q2)都在物线y=ax2+bx+m上,
∴q1=﹣(﹣2.5+1)2=﹣,q2=﹣(1+1)2=﹣4,
∴q1>q2,
故选:A.
8.解:①∵抛物线开口向下,
∴a<0,
∵抛物线的对称轴为直线x=﹣=1,
∴b=﹣2a>0,
∴ab<0,所以①正确,符合题意;
②∵x=﹣1时,y<0,
即a﹣b+1<0,
∵b=﹣2a,
∴a=﹣,
∴﹣﹣b+1<0,
∴b>,所以②错误,不符合题意;
③当x=1时,y=a+b+1=a﹣2a+1=﹣a+1,
∴抛物线的顶点坐标为(1,﹣a+1),
把(1,﹣a+1)代入y=kx+1得﹣a+1=k+1,
∴a=﹣k,所以③正确,符合题意;
④当0<x<1时,ax2+bx+1>kx+1,
即ax2+bx>kx,
∴ax+b>k,所以④正确,符合题意.
故选:B.
9.解:观察图象可得,在0≤x≤4时,图象有最高点和最低点,
∴函数有最大值2和最小值﹣2.5,
故选:A.
10.解:根据题意y=x2+bx+c=(x+)2+c﹣下平移2个单位,再向左平移1个单位,得y=(x++1)2+c﹣﹣2.
∵抛物线的顶点坐标为(﹣2,1),
∴﹣﹣1=﹣2,c﹣﹣2=1,
解得:b=2,c=4,
∴b﹣c=﹣2,
故答案为:﹣2.
11.解:y=﹣2(x﹣1)2﹣3,
∵a=﹣2<0,
∴当x=1时,y有最大值,最大值为﹣3.
故答案为﹣3.
12.解:在Rt△ABC中,∠C=90°,AB=10cm,BC=8cm,
∴AC==6cm.
设运动时间为ts(0≤t≤4),则PC=(6﹣t)cm,CQ=2tcm,
∴S四边形PABQ=S△ABC﹣S△CPQ=AC BC﹣PC CQ=×6×8﹣(6﹣t)×2t=t2﹣6t+24=(t﹣3)2+15,
∴当t=3时,四边形PABQ的面积取最小值,最小值为15cm2.
故答案为15.
13.解:∵当x=0和x=2时的函数值相等,
∴二次函数图象的对称轴x==1,
∵对称轴x=﹣=m,
∴m=1,即m=2,
故答案为:2.
14.解:当x=0时,y=﹣x2+2x+3=3,则C(0,3),
∵△PCD是以CD为底的等腰三角形,
∴点P为直线y=2与抛物线y=﹣x2+2x+3的交点,
当y=2时,﹣x2+2x+3=2,解得x1=1+,x2=1﹣,
∴P点坐标为(1+,2)或(1﹣,2).
故答案为(1+,2)或(1﹣,2).
15.解:当x=1时,y=x2=,则P1(1,),所以S1=×1×=;
当x=2时,y=x2=2,则P2(2,2),所以S2=×1×(2﹣)=;
当x=3时,y=x2=,则P3(3,),所以S3=×1×(﹣2)=,
同样方法可得S4=,
所以Sn=.
故答案为,.
16.解:∵m1为y=﹣x(x﹣1)=﹣(x﹣)2+(0≤x≤1),
∴则P1的纵坐标为,
∵OA1=1,OA2=2,
∴P2(,﹣),
∴P10的横坐标是=,
p10的纵坐标是﹣,
故答案为,(,﹣).
17.解:y=x2﹣2x+2=(x﹣1)2+1,分类讨论:
(1)若顶点横坐标在范围t≤x≤t+1右侧时,有t+1<1,即t<0,此时y随x的增大而减小,
∴当x=t+1时,函数取得最小值,y最小值=t=(t+1)2﹣2(t+1)+2,
方程无解.
(2)若顶点横坐标在范围t≤x≤t+1内时,即有t≤1≤t+1,
解这个不等式,即 0≤t≤1.此时当x=1时,函数取得最小值,y最小值=1,
∴t=1.
(3)若顶点横坐标在范围t≤x≤t+1左侧时,即t>1时,y随x的增大而增大,
∵当x=t时,函数取得最小值,y最小值=t=t2﹣2t+2,解得t=2或1(舍弃),
∴t=1或2.
故答案为:1或2.
18.解:二次函数对称轴为直线x=m,
①m<﹣2时,x=﹣2取得最大值,﹣(﹣2﹣m)2+m2+1=4,
解得m=﹣,不合题意,舍去;
②﹣2≤m≤1时,x=m取得最大值,m2+1=4,
解得m=±,
∵m=不满足﹣2≤m≤1的范围,
∴m=﹣;
③m>1时,x=1取得最大值,﹣(1﹣m)2+m2+1=4,
解得m=2.
综上所述,m=2或﹣时,二次函数有最大值4.
故答案是:2或﹣.
19.解:∵抛物线y=(k﹣1)x2+2kx+3k﹣2的图象最高点在x轴上,
∴k﹣1<0且△=4k2﹣4(k﹣1)(3k﹣2)=0,解得k1=2(舍去),k2=,
即k的值为.
20.解:联立,
解得,,
所以,min{﹣x2+1,﹣x}的最大值是.
故答案为:.
21.解:分三种情况:
当﹣a<﹣1,即a>1时,二次函数y=x2+2ax+a在﹣1≤x≤2上为增函数,
所以当x=﹣1时,y有最小值为﹣4,把(﹣1,﹣4)代入y=x2+2ax+a中解得:a=5;
当﹣a>2,即a<﹣2时,二次函数y=x2+2ax+a在﹣1≤x≤2上为减函数,
所以当x=2时,y有最小值为﹣4,把(2,﹣4)代入y=x2+2ax+a中解得:a=﹣>﹣2,舍去;
当﹣1≤﹣a≤2,即﹣2≤a≤1时,此时抛物线的顶点为最低点,
所以顶点的纵坐标为=﹣4,解得:a=或a=>1,舍去.
综上,a的值为5或.
故答案为:5或
22.解:(1)∵S△PBQ=PB BQ,PB=AB﹣AP=16﹣2x,BQ=x,
∴y=(16﹣2x)x,
即y=﹣x2+8x(0<x≤4);
(2)由(1)知:y=﹣x2+8x,
∴y=﹣(x﹣4)2+16,
∴当x=4时,y有最大值,
即△BPQ面积有最大值时,x的值为4.
23.解:(1)由题意:BQ=2t cm,PB=(6﹣t)cm,
故答案为2t,(6﹣t).
(2)由题意,得.
解得(不合题意,舍去),t2=3.
所以当t=3秒时,PQ的长度等于;
(3)存在.理由如下:
设五边形APQCD的面积为S.
∵S矩形ABCD=6×8=48(cm2),
∴,
∴当t=3秒时,五边形APQCD的面积有最小值,最小值为39cm2.
24.解:(1)y=﹣x2+2x+1=﹣(x﹣1)2+2,将二次函数y=﹣x2+2x+1的图象向右平移3个单位,向下平移2个单位得到的函数解析式为:y=﹣(x﹣1﹣3)2+2﹣2,即y=﹣(x﹣4)2;
故答案为y=﹣(x﹣4)2;
(2)y=﹣x2+2x+1=﹣(x﹣1)2+2,将原抛物线绕顶点旋转180°后,得:y=(x﹣1)2+2;
故答案为:y=(x﹣1)2+2;
(3)二次函数y=﹣x2+2x+1的图象绕原点旋转180°后,得到的图象的解析式为﹣y=﹣(﹣x)2+2(﹣x)+1
即y=x2+2x﹣1,
故答案为:y=x2+2x﹣1;
(4)y=﹣x2+2x+1=﹣(x﹣1)2+2,
此抛物线的顶点坐标为:(1,2),
∵将二次函数的图象沿x轴翻折,得到一个新的抛物线,
∴新的抛物线顶点坐标为:(1,﹣2),a=1,
∴新抛物线的解析式为:y=(x﹣1)2﹣2,
故答案为y=(x﹣1)2﹣2;
(5)y=﹣x2+2x+1=﹣(x﹣1)2+2,
此抛物线的顶点坐标为:(1,2),
∵将二次函数的图象沿y轴翻折,得到一个新的抛物线,
∴新的抛物线顶点坐标为:(﹣1,2),a=﹣1,
∴新抛物线的解析式为:y=﹣(x+1)2+2,
故答案为y=﹣(x+1)2+2.
25.解:(1)当x≥2x﹣1时,即x≤1时,x*(2x﹣1)=x2+2x﹣1,
当x<2x﹣1时,即x>1时,x*(2x﹣1)=;
(2)∵函数y=x*(2x﹣1)的图象的图象由抛物线,反比例函数各一部分构成,
又∵A、B两点关于坐标原点成中心对称,
∴x2=1,
∴A(﹣1,﹣2);
(3)由图象可知,x1<﹣1﹣,1>x2>﹣1+,x3>1,
x2+2x﹣1=m,则x1,x2=﹣m﹣1,
=m,则x3=,
∴t=x1+2x2+x3+x1x2x3=﹣2+x2++(﹣m﹣1)=x2,
∴﹣1+<t<1,
故答案为﹣1+<t<1.
26.解:(1)∵BC=DC,CE=CF=x,
∴BE=DF=4﹣x,
∴y=S正方形ABCD﹣S△ABE﹣S△ADF﹣S△CEF,
∴y=42﹣×(4﹣x)﹣×4×(4﹣x)﹣x2
∴y=﹣2+4x(0<x≤4).
(2)∵y=﹣2+4x=﹣(x﹣4)2+8,
∴当x=4时,△AEF的面积最大,此时△AEF的面积是8.
27.解:(1)∵动点P从点A开始沿边AB向点B以2cm/s的速度移动.动点Q从点B开始沿边BC向点C以4cm/s的速度移动,
∴根据题意得出:
y=PB×BQ=(12﹣2x)×4x=﹣4x2+24x(0≤x<6);
(2)因为S=﹣4x2+24x=﹣4(x﹣3)2+36,
所以3秒后△PBQ的面积最大,最大面积是36cm2.
28.解:(1)﹣2x2﹣4x+3=﹣2(x2+2x+1﹣1)+3=2(x+1)2+5≤5,
∴﹣2x2﹣4x+3有最大值是5,
故答案为:5;
(2)解:由x2+3x+y﹣3=0得
y=﹣x2﹣3x+3,把y代入x+y得:
y﹣x=x2﹣3x+3﹣x=﹣x2﹣4x+3=﹣(x+2)2+3+4≤7,
∴y﹣x的最大值为7.
故答案为:7.
(3)解:设利用墙的一边长为x,则x≤16,
由题意知:S花圃=x =﹣x2+14x=﹣(x﹣14)2+98
当x=14时,花圃面积最大,最大面积为98m2.
同步练习题(附答案)
一.选择题
1.把抛物线y=x2+1向左平移1个单位,则平移后抛物线的解析式为( )
A.y=(x+1)2+1 B.y=(x﹣1)2+1 C.y=x2+2 D.y=x2
2.点P1(﹣2,y1),P2(2,y2),P3(4,y3)均在二次函数y=﹣x2+2x+c的图象上,则y1,y2,y3的大小关系是( )
A.y2>y3>y1 B.y2>y1=y3 C.y1=y3>y2 D.y1=y2>y3
3.若函数y=x2﹣4x+m的图象上有两点A(x1,y1),B(x2,y2),若x1<x2<2,则( )
A.y1>y2 B.y1<y2
C.y1=y2 D.y1,y2的大小不确定
4.如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴为x=且经过点(2,0).下列说法:①abc<0;②4a+2b+c<0;③﹣2b+c=0;④若(﹣,y1),(,y2)是抛物线上的两点,则y1<y2;⑤b>m(am+b)(其中m≠).其中说法正确的是( )
①③④⑤ B.①②④
C.①④⑤ D.③④⑤
5.二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①abc>0,②2a+b=0,③b<a+c,④3a+c=0,其中错误的结论有( )
A.1个 B.2个 C.3个 D.4个
6.二次函数y=ax2+bx+c的部分图象如图,图象过点A(3,0),对称轴为直线x=1,下列结论:①a﹣b+c=0;②2a+b=0; ③4ac﹣b2>0;④a+b≥am2+bm(m为实数);⑤3a+c>0.则其中正确的结论有( )
A.2个 B.3个 C.4个 D.5个
7.已知抛物线y=ax2+bx+m是由抛物线y=﹣x2+2x+2先关于y轴作轴对称图形,再将所得的图象向下平移3个单位长度得到的,点Q1(﹣2.5,q1)、Q2(1,q2)都在抛物线y=ax2+bx+m上,则q1,q2的大小关系是( )
A.q1>q2 B.q1=q2 C.q1<q2 D.不能确定
8.如图,抛物线y=ax2+bx+1的顶点在直线y=kx+1上,对称轴为直线x=1,有以下四个结论:①ab<0,②b<,③a=﹣k,④当0<x<1时,ax+b>k,其中正确的结论是( )
A.①②③ B.①③④ C.①②④ D.②③④
9.已知二次函数的图象(0≤x≤4)如图,关于该函数在所给自变量的取值范围内,下列说法正确的是( )
A.有最大值2,有最小值﹣2.5
B.有最大值2,有最小值1.5
C.有最大值1.5,有最小值﹣2.5
D.有最大值2,无最小值
二.填空题
10.把二次函数y=x2+bx+c的图象向下平移2个单位长度,再向左平移1个单位长度后,得到的抛物线的顶点坐标为(﹣2,1),则b﹣c的值为 .
11.二次函数y=﹣2(x﹣1)2﹣3的最大值是 .
12.如图,在△ABC中,∠C=90°,AB=10cm,BC=8cm,点P从点A沿AC向点C以1cm/s的速度运动,同时点Q从点C沿CB向点B以2cm/s的速度运动(点Q运动到点B停止),在运动过程中,四边形PABQ的面积最小值为 cm2.
13.已知二次函数y=x2﹣mx+3在x=0和x=2时的函数值相等,那么m的值是 .
14.如图,抛物线y=﹣x2+2x+3与y轴交于点C,点D(0,1),点P是抛物线上的动点,若△PCD是以CD为底的等腰三角形,则点P的坐标为 .
15.如图已知A1,A2,A3,…An是x轴上的点,且OA1=A1A2=A2A3=A3A4=…=An﹣1An=1,分别过点A1,A2,A3,…An′作x轴的垂线交二次函数y=x2(x>0)的图象于点P1,P2,P3,…Pn,若记△OA1P1的面积为S1,过点P1作P1B1⊥A2P2于点B1,记△P1B1P2的面积为S2,过点P2作P2B2⊥A3P3于点B2,记△P2B2P3的面积为S3,…依次进行下去,则S3= ,最后记△Pn﹣1Bn﹣1Pn(n>1)的面积为Sn,则Sn= .
16.如图,一段抛物线y=﹣x(x﹣1)(0≤x≤1)记为m1,它与x轴交点为O,A1,顶点为P1;将m1绕点A1旋转180°得m2,交x轴于点A2,顶点为P2;将m2绕点A2旋转180°得m3,交x轴于点A3,顶点为P3,…,如此进行下去,直至得m10,顶点为P10,则P1的纵坐标为 ,P10的坐标为 .
17.已知二次函数y=x2﹣2x+2在t≤x≤t+1时的最小值是t,则t的值为 .
18.当﹣2≤x≤1时,二次函数y=﹣(x﹣m)2+m2+1有最大值4,则实数m的值为 .
19.抛物线y=(k﹣1)x2+2kx+3k﹣2的图象最高点在x轴上,则k的值为 .
20.定义符号min{a,b}的含义为:当a≥b时,min{a,b}=b;当a<b时,min{a,b}=a.如:min{1,﹣3}=﹣3,min{﹣4,﹣2}=﹣4.则min{﹣x2+1,﹣x}的最大值是 .
21.二次函数y=x2+2ax+a在﹣1≤x≤2上有最小值﹣4,则a的值为 .
三.解答题
22.如图,矩形ABCD的两边长AB=16cm,AD=4cm,点P,Q分别从A,B同时出发,P在边AB上沿AB方向以每秒2cm的速度匀速运动,Q在边BC上沿BC方向以每秒1cm的速度匀速运动设运动时间为x(秒),设△BPQ的面积为ycm2.
(1)求y关于x的函数关系式,并写出x的取值范围;
(2)当△BPQ面积有最大值时,求x的值.
23.如图,在矩形ABCD中,AB=6cm,BC=8cm,点P从点A开始沿边AB向终点B以1cm/s的速度移动,与此同时,点Q从点B开始沿边BC向终点C以2cm/s的速度移动.如果P,Q分别从A,B同时出发,当点Q运动到点C时,两点停止运动,设运动时间为t秒.
(1)填空:BQ= ,PB= ;(用含t的代数式表示)
(2)当t为何值时,PQ的长度等于3cm?
(3)当t为何值时,五边形APQCD的面积有最小值?最小值为多少?
24.将二次函数y=﹣x2+2x+1的图象
(1)向右平移3个单位,向下平移2个单位得到的函数解析式是 ;
(2)绕它的顶点旋转180°所得抛物线解析式为 ;
(3)绕原点旋转180°所得抛物线解析式为 ;
(4)求沿x轴翻折所得抛物线解析式;
(5)求沿y轴翻折所得抛物线解析式为.
25.对实数a,b,定义运算“*”为:a*b=
(1)求函数y=x*(2x﹣1)的解析式;
(2)若点A(x1,y1)、B(x2,y2)(x1<x2)在函数y=x*(2x﹣1)的图象上,且A、B两点关于坐标原点成中心对称,求点A的坐标;
(3)关于x的方程x*(2x﹣1)=m恰有三个互不相等的实数根x1,x2,x3,且x1<x2<x3,设t=x1+2x2+x3+x1x2x3,则t的取值范围是 .
26.如图,点E、F分别是正方形ABCD的边BC、CD上两点,且CE=CF,AB=4.
(1)设CE=x,△AEF的面积为y,求y关于x的函数关系式;
(2)当x取何值时,△AEF面积最大?求出此时△AEF的面积.
27.如图,在△ABC中,∠B=90°,AB=12cm,BC=24cm,点P,Q分别从A,B两点同时出发,点P从点A开始沿边AB向点B以2cm/s的速度匀速运动,点Q从点B开始沿BC边向点C以4cm/s的速度匀速运动,设运动时间为xs,△PBQ的面积为ycm2.
(1)求y与x之间的函数解析式,并写出x的取值范围;
(2)求△PBQ的面积的最大值.
28.阅读下面的材料,回答问题:
爱动脑筋的小明发现二次三项式也可以配方,从而解决一些问题.
例如:x2﹣2x+2=(x2﹣2x+1)+1=(x﹣1)2+1≥1;因此x2﹣2x+2有最小值是1.
(1)尝试:﹣2x2﹣4x+3=﹣2(x2+2x+1﹣1)+3=﹣2(x+1)2+5,因此﹣2x2﹣4x+3有最大值是 ;
(2)拓展:已知实数x,y满足x2+3x+y﹣3=0,则y﹣x的最大值为 ;
(3)应用:有长为28米的篱笆,一面利用墙(墙的最大可用长度为16米),围成一个长方形的花圃.能围成面积最大的花圃吗?如果能,请求出最大面积.
参考答案
1.解:由“左加右减”的原则可知,把抛物线y=x2+1向左平移1个单位,则平移后抛物线的解析式为:y=(x+1)2+1,
故选:A.
2.解:∵y=﹣x2+2x+c=﹣(x﹣1)2+1+c,
∴图象的开口向下,对称轴是直线x=1,
A(﹣2,y1)关于对称轴的对称点为(4,y1),
∵2<4,
∴y2>y1=y3,
故选:B.
3.解:∵y=x2﹣4x+m,
∴此函数的对称轴为:x=﹣=﹣=2,
∵x1<x2<2,两点都在对称轴左侧,a=1>0,
∴对称轴左侧y随x的增大而减小,
∴y1>y2.
故选:A.
4.解:∵抛物线开口向下,
∴a<0,
∵抛物线对称轴为直线x=﹣=,
∴b=﹣a>0,
∵抛物线与y轴的交点在x轴上方,
∴c>0,
∴abc<0,所以①正确;
∵抛物线经过点(2,0),
∴x=2时,y=0,
∴4a+2b+c=0,所以②错误;
∵对称轴为x=,且经过点(2,0),
∴抛物线与x轴的另一个交点为(﹣1,0),
∴=﹣1×2=﹣2,
∴c=﹣2a,
∴﹣2b+c=2a﹣2a=0,所以③正确;
∵点(﹣,y1)离对称轴要比点(,y2)离对称轴要远,
∴y1<y2,所以④正确.
∵抛物线的对称轴为直线x=,
∴当x=时,y有最大值,
∴a+b+c>am2+bm+c(其中m≠),
∴a+b>m(am+b)(其中m≠),
∵a=﹣b,
∴﹣b+b>m(am+b),
∴b>m(am+b),所以⑤正确;
故选:A.
5.解:∵抛物线开口向上,
∴a>0,
∵抛物线的对称轴为直线x=﹣=1,
∴b=﹣2a<0,
∴2a+b=0,
∵抛物线与y轴的交点在x轴下方,
∴c<0,
∴abc>0,所以①②正确;
∴抛物线与x轴的一个交点坐标为(﹣1,0),
∴y=a﹣b+c=0,
∴b=﹣2a,
∴a+c=b,a+2a+c=0,
∴3a+c=0,所以③错误;④正确.
故选:A.
6.解:∵二次函数y=ax2+bx+c的图象过点A(3,0),对称轴为直线x=1,
∴点A(3,0)关于直线x=1对称点为(﹣1,0),
∴当x=﹣1时,y=0,即a﹣b+c=0.故①正确;
∵对称轴为直线x=1,
∴﹣=1,
∴b=﹣2a,
∴2a+b=0,故②正确;
∵抛物线与x轴有两个交点,
∴Δ=b2﹣4ac>0,
∴4ac﹣b2<0,故③错误;
∵当x=1时,函数有最大值,
∴a+b+c≥am2+bm+c,
∴a+b≥am2+bm,故④正确;
∵b=﹣2a,a﹣b+c=0,
∴a+2a+c=0,即3a+c=0,故⑤错误;
综上,正确的有①②④.
故选:B.
7.解:∵y=﹣x2+2x+2=﹣(x﹣1)2+3,
∴顶点为(1,3)
∴抛物线y=﹣x2+2x+2先作关于y轴的轴对称抛物线的顶点为(﹣1,3),再向下平移3个单位长度顶点为(﹣1,0),
∴抛物线y=ax2+bx+m的解析式为y=﹣(x+1)2,
∵点Q1(﹣2.5,q1)、Q2(1,q2)都在物线y=ax2+bx+m上,
∴q1=﹣(﹣2.5+1)2=﹣,q2=﹣(1+1)2=﹣4,
∴q1>q2,
故选:A.
8.解:①∵抛物线开口向下,
∴a<0,
∵抛物线的对称轴为直线x=﹣=1,
∴b=﹣2a>0,
∴ab<0,所以①正确,符合题意;
②∵x=﹣1时,y<0,
即a﹣b+1<0,
∵b=﹣2a,
∴a=﹣,
∴﹣﹣b+1<0,
∴b>,所以②错误,不符合题意;
③当x=1时,y=a+b+1=a﹣2a+1=﹣a+1,
∴抛物线的顶点坐标为(1,﹣a+1),
把(1,﹣a+1)代入y=kx+1得﹣a+1=k+1,
∴a=﹣k,所以③正确,符合题意;
④当0<x<1时,ax2+bx+1>kx+1,
即ax2+bx>kx,
∴ax+b>k,所以④正确,符合题意.
故选:B.
9.解:观察图象可得,在0≤x≤4时,图象有最高点和最低点,
∴函数有最大值2和最小值﹣2.5,
故选:A.
10.解:根据题意y=x2+bx+c=(x+)2+c﹣下平移2个单位,再向左平移1个单位,得y=(x++1)2+c﹣﹣2.
∵抛物线的顶点坐标为(﹣2,1),
∴﹣﹣1=﹣2,c﹣﹣2=1,
解得:b=2,c=4,
∴b﹣c=﹣2,
故答案为:﹣2.
11.解:y=﹣2(x﹣1)2﹣3,
∵a=﹣2<0,
∴当x=1时,y有最大值,最大值为﹣3.
故答案为﹣3.
12.解:在Rt△ABC中,∠C=90°,AB=10cm,BC=8cm,
∴AC==6cm.
设运动时间为ts(0≤t≤4),则PC=(6﹣t)cm,CQ=2tcm,
∴S四边形PABQ=S△ABC﹣S△CPQ=AC BC﹣PC CQ=×6×8﹣(6﹣t)×2t=t2﹣6t+24=(t﹣3)2+15,
∴当t=3时,四边形PABQ的面积取最小值,最小值为15cm2.
故答案为15.
13.解:∵当x=0和x=2时的函数值相等,
∴二次函数图象的对称轴x==1,
∵对称轴x=﹣=m,
∴m=1,即m=2,
故答案为:2.
14.解:当x=0时,y=﹣x2+2x+3=3,则C(0,3),
∵△PCD是以CD为底的等腰三角形,
∴点P为直线y=2与抛物线y=﹣x2+2x+3的交点,
当y=2时,﹣x2+2x+3=2,解得x1=1+,x2=1﹣,
∴P点坐标为(1+,2)或(1﹣,2).
故答案为(1+,2)或(1﹣,2).
15.解:当x=1时,y=x2=,则P1(1,),所以S1=×1×=;
当x=2时,y=x2=2,则P2(2,2),所以S2=×1×(2﹣)=;
当x=3时,y=x2=,则P3(3,),所以S3=×1×(﹣2)=,
同样方法可得S4=,
所以Sn=.
故答案为,.
16.解:∵m1为y=﹣x(x﹣1)=﹣(x﹣)2+(0≤x≤1),
∴则P1的纵坐标为,
∵OA1=1,OA2=2,
∴P2(,﹣),
∴P10的横坐标是=,
p10的纵坐标是﹣,
故答案为,(,﹣).
17.解:y=x2﹣2x+2=(x﹣1)2+1,分类讨论:
(1)若顶点横坐标在范围t≤x≤t+1右侧时,有t+1<1,即t<0,此时y随x的增大而减小,
∴当x=t+1时,函数取得最小值,y最小值=t=(t+1)2﹣2(t+1)+2,
方程无解.
(2)若顶点横坐标在范围t≤x≤t+1内时,即有t≤1≤t+1,
解这个不等式,即 0≤t≤1.此时当x=1时,函数取得最小值,y最小值=1,
∴t=1.
(3)若顶点横坐标在范围t≤x≤t+1左侧时,即t>1时,y随x的增大而增大,
∵当x=t时,函数取得最小值,y最小值=t=t2﹣2t+2,解得t=2或1(舍弃),
∴t=1或2.
故答案为:1或2.
18.解:二次函数对称轴为直线x=m,
①m<﹣2时,x=﹣2取得最大值,﹣(﹣2﹣m)2+m2+1=4,
解得m=﹣,不合题意,舍去;
②﹣2≤m≤1时,x=m取得最大值,m2+1=4,
解得m=±,
∵m=不满足﹣2≤m≤1的范围,
∴m=﹣;
③m>1时,x=1取得最大值,﹣(1﹣m)2+m2+1=4,
解得m=2.
综上所述,m=2或﹣时,二次函数有最大值4.
故答案是:2或﹣.
19.解:∵抛物线y=(k﹣1)x2+2kx+3k﹣2的图象最高点在x轴上,
∴k﹣1<0且△=4k2﹣4(k﹣1)(3k﹣2)=0,解得k1=2(舍去),k2=,
即k的值为.
20.解:联立,
解得,,
所以,min{﹣x2+1,﹣x}的最大值是.
故答案为:.
21.解:分三种情况:
当﹣a<﹣1,即a>1时,二次函数y=x2+2ax+a在﹣1≤x≤2上为增函数,
所以当x=﹣1时,y有最小值为﹣4,把(﹣1,﹣4)代入y=x2+2ax+a中解得:a=5;
当﹣a>2,即a<﹣2时,二次函数y=x2+2ax+a在﹣1≤x≤2上为减函数,
所以当x=2时,y有最小值为﹣4,把(2,﹣4)代入y=x2+2ax+a中解得:a=﹣>﹣2,舍去;
当﹣1≤﹣a≤2,即﹣2≤a≤1时,此时抛物线的顶点为最低点,
所以顶点的纵坐标为=﹣4,解得:a=或a=>1,舍去.
综上,a的值为5或.
故答案为:5或
22.解:(1)∵S△PBQ=PB BQ,PB=AB﹣AP=16﹣2x,BQ=x,
∴y=(16﹣2x)x,
即y=﹣x2+8x(0<x≤4);
(2)由(1)知:y=﹣x2+8x,
∴y=﹣(x﹣4)2+16,
∴当x=4时,y有最大值,
即△BPQ面积有最大值时,x的值为4.
23.解:(1)由题意:BQ=2t cm,PB=(6﹣t)cm,
故答案为2t,(6﹣t).
(2)由题意,得.
解得(不合题意,舍去),t2=3.
所以当t=3秒时,PQ的长度等于;
(3)存在.理由如下:
设五边形APQCD的面积为S.
∵S矩形ABCD=6×8=48(cm2),
∴,
∴当t=3秒时,五边形APQCD的面积有最小值,最小值为39cm2.
24.解:(1)y=﹣x2+2x+1=﹣(x﹣1)2+2,将二次函数y=﹣x2+2x+1的图象向右平移3个单位,向下平移2个单位得到的函数解析式为:y=﹣(x﹣1﹣3)2+2﹣2,即y=﹣(x﹣4)2;
故答案为y=﹣(x﹣4)2;
(2)y=﹣x2+2x+1=﹣(x﹣1)2+2,将原抛物线绕顶点旋转180°后,得:y=(x﹣1)2+2;
故答案为:y=(x﹣1)2+2;
(3)二次函数y=﹣x2+2x+1的图象绕原点旋转180°后,得到的图象的解析式为﹣y=﹣(﹣x)2+2(﹣x)+1
即y=x2+2x﹣1,
故答案为:y=x2+2x﹣1;
(4)y=﹣x2+2x+1=﹣(x﹣1)2+2,
此抛物线的顶点坐标为:(1,2),
∵将二次函数的图象沿x轴翻折,得到一个新的抛物线,
∴新的抛物线顶点坐标为:(1,﹣2),a=1,
∴新抛物线的解析式为:y=(x﹣1)2﹣2,
故答案为y=(x﹣1)2﹣2;
(5)y=﹣x2+2x+1=﹣(x﹣1)2+2,
此抛物线的顶点坐标为:(1,2),
∵将二次函数的图象沿y轴翻折,得到一个新的抛物线,
∴新的抛物线顶点坐标为:(﹣1,2),a=﹣1,
∴新抛物线的解析式为:y=﹣(x+1)2+2,
故答案为y=﹣(x+1)2+2.
25.解:(1)当x≥2x﹣1时,即x≤1时,x*(2x﹣1)=x2+2x﹣1,
当x<2x﹣1时,即x>1时,x*(2x﹣1)=;
(2)∵函数y=x*(2x﹣1)的图象的图象由抛物线,反比例函数各一部分构成,
又∵A、B两点关于坐标原点成中心对称,
∴x2=1,
∴A(﹣1,﹣2);
(3)由图象可知,x1<﹣1﹣,1>x2>﹣1+,x3>1,
x2+2x﹣1=m,则x1,x2=﹣m﹣1,
=m,则x3=,
∴t=x1+2x2+x3+x1x2x3=﹣2+x2++(﹣m﹣1)=x2,
∴﹣1+<t<1,
故答案为﹣1+<t<1.
26.解:(1)∵BC=DC,CE=CF=x,
∴BE=DF=4﹣x,
∴y=S正方形ABCD﹣S△ABE﹣S△ADF﹣S△CEF,
∴y=42﹣×(4﹣x)﹣×4×(4﹣x)﹣x2
∴y=﹣2+4x(0<x≤4).
(2)∵y=﹣2+4x=﹣(x﹣4)2+8,
∴当x=4时,△AEF的面积最大,此时△AEF的面积是8.
27.解:(1)∵动点P从点A开始沿边AB向点B以2cm/s的速度移动.动点Q从点B开始沿边BC向点C以4cm/s的速度移动,
∴根据题意得出:
y=PB×BQ=(12﹣2x)×4x=﹣4x2+24x(0≤x<6);
(2)因为S=﹣4x2+24x=﹣4(x﹣3)2+36,
所以3秒后△PBQ的面积最大,最大面积是36cm2.
28.解:(1)﹣2x2﹣4x+3=﹣2(x2+2x+1﹣1)+3=2(x+1)2+5≤5,
∴﹣2x2﹣4x+3有最大值是5,
故答案为:5;
(2)解:由x2+3x+y﹣3=0得
y=﹣x2﹣3x+3,把y代入x+y得:
y﹣x=x2﹣3x+3﹣x=﹣x2﹣4x+3=﹣(x+2)2+3+4≤7,
∴y﹣x的最大值为7.
故答案为:7.
(3)解:设利用墙的一边长为x,则x≤16,
由题意知:S花圃=x =﹣x2+14x=﹣(x﹣14)2+98
当x=14时,花圃面积最大,最大面积为98m2.
