第3章二次函数 单元练习题 2021-2022学年鲁教版(五四制)九年级数学上册(Word版含答案)
文档属性
| 名称 | 第3章二次函数 单元练习题 2021-2022学年鲁教版(五四制)九年级数学上册(Word版含答案) | 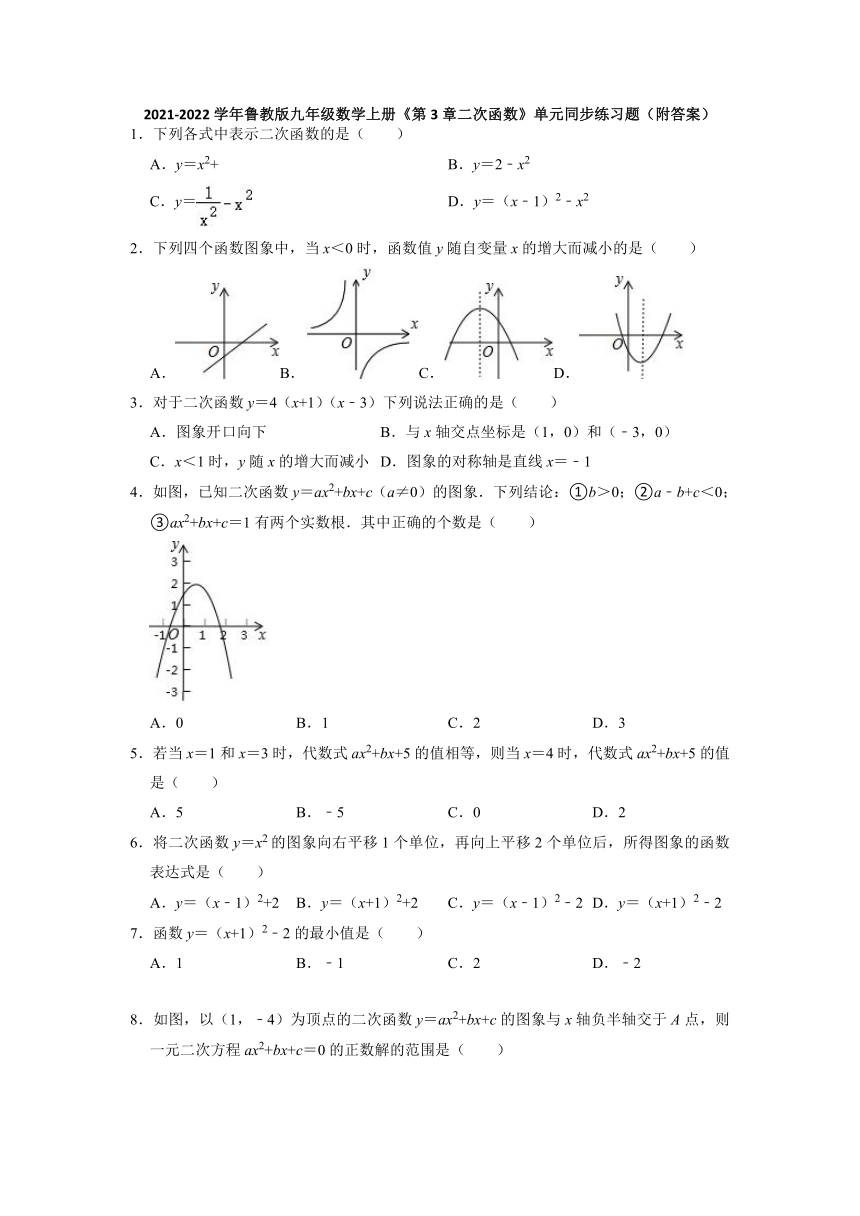 | |
| 格式 | doc | ||
| 文件大小 | 426.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-28 11:03:51 | ||
图片预览




文档简介
2021-2022学年鲁教版九年级数学上册《第3章二次函数》单元同步练习题(附答案)
1.下列各式中表示二次函数的是( )
A.y=x2+ B.y=2﹣x2
C.y= D.y=(x﹣1)2﹣x2
2.下列四个函数图象中,当x<0时,函数值y随自变量x的增大而减小的是( )
A.B.C.D.
3.对于二次函数y=4(x+1)(x﹣3)下列说法正确的是( )
A.图象开口向下 B.与x轴交点坐标是(1,0)和(﹣3,0)
C.x<1时,y随x的增大而减小 D.图象的对称轴是直线x=﹣1
4.如图,已知二次函数y=ax2+bx+c(a≠0)的图象.下列结论:①b>0;②a﹣b+c<0;③ax2+bx+c=1有两个实数根.其中正确的个数是( )
A.0 B.1 C.2 D.3
5.若当x=1和x=3时,代数式ax2+bx+5的值相等,则当x=4时,代数式ax2+bx+5的值是( )
A.5 B.﹣5 C.0 D.2
6.将二次函数y=x2的图象向右平移1个单位,再向上平移2个单位后,所得图象的函数表达式是( )
A.y=(x﹣1)2+2 B.y=(x+1)2+2 C.y=(x﹣1)2﹣2 D.y=(x+1)2﹣2
7.函数y=(x+1)2﹣2的最小值是( )
A.1 B.﹣1 C.2 D.﹣2
8.如图,以(1,﹣4)为顶点的二次函数y=ax2+bx+c的图象与x轴负半轴交于A点,则一元二次方程ax2+bx+c=0的正数解的范围是( )
A.2<x<3 B.3<x<4 C.4<x<5 D.5<x<6
9.如图,直线y1=kx+n(k≠0)与抛物线y2=ax2+bx+c(a≠0)分别交于A(﹣1,0),B(2,﹣3)两点,那么当y1>y2时,x的取值范围是( )
A.﹣1<x<2 B.x>2 C.x<﹣1或x>2 D.x≤﹣1
10.长方形的周长为24cm,其中一边长为xcm(其中x>0),面积为ycm2,则这样的长方形中y与x的关系可以写为( )
A.y=x2 B.y=12﹣x2 C.y=(12﹣x) x D.y=2(12﹣x)
11.如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴正半轴相交于A、B两点,与y轴相交于点C,对称轴为直线x=2,且OA=OC,则下列结论:
①abc>0;②9a+3b+c<0;③c>﹣1;④关于x的方程ax2+bx+c=0(a≠0)有一个根为﹣
其中正确的结论个数有( )
A.1个 B.2个 C.3个 D.4个
12.函数y=(m+1)x|m|+1+5x﹣5是二次函数,则m= .
13.如图,已知函数y=﹣与y=ax2+bx(a>0,b>0)的图象交于点P,点P的纵坐标为1,则关于x的方程ax2+bx+=0的解是 .
14.已知抛物线y=(x﹣m)2+3,当x>1时,y随x的增大而增大,则m的取值范围是 .
15.在平面直角坐标系中,把抛物线y=﹣2x2向下平移2个单位长度,再向左平移1个单位长度,得到的新抛物线解析式为 .
16.有这样一个问题:探究函数y=x2+的图象与性质,小东根据学习函数的经验,对函数y=x2+的图象与性质进行了探究,下面是小东的探究过程,请补充完整:
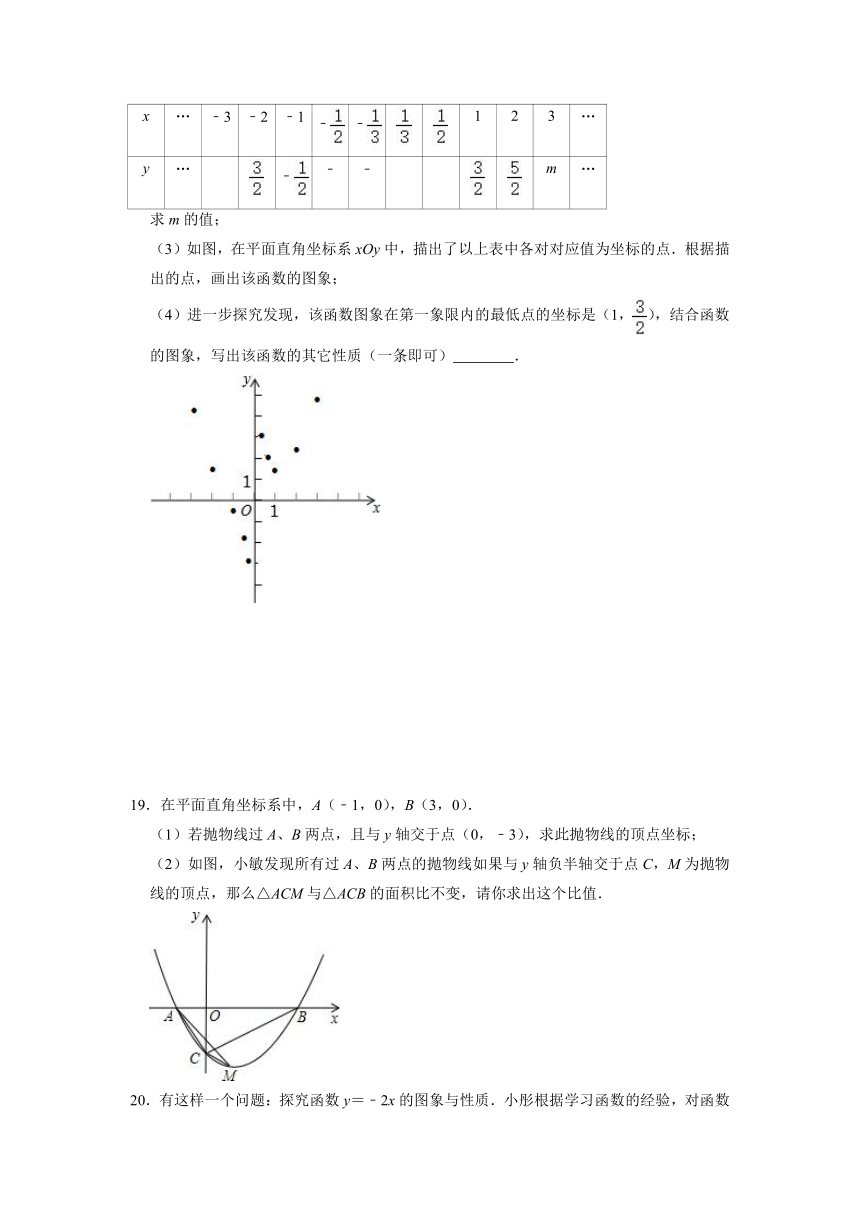
(1)下表是y与x的几组对应值.
x … ﹣3 ﹣2 ﹣1 1 2 3 …
y … ﹣ m …
函数y=x2+的自变量x的取值范围是 ,m的值为 ;
(2)在如图所示的平面直角坐标系xOy中,描出以上表中各对对应值为坐标的点.并画出该函数的大致图象;
(3)进一步探究函数图象发现:
①函数图象与x轴有 个交点,所以对应方程x2+=0有 个实数根;
②方程x2+=2有 个实数根;
③结合函数的图象,写出该函数的一条性质 .
17.某班“数学兴趣小组”对函数y=x2﹣2|x|的图象和性质进行了探究,探究过程如下,请补充完整.
(1)自变量x的取值范围是全体实数,x与y的几组对应值列表如下:
x … ﹣3 ﹣ ﹣2 ﹣1 0 1 2 3 …
y … 3 m ﹣1 0 ﹣1 0 3 …
其中,m= .
(2)根据表中数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请画出该函数图象的另一部分.
(3)观察函数图象,写出两条函数的性质.
(4)进一步探究函数图象发现:
①函数图象与x轴有 个交点,所以对应的方程x2﹣2|x|=0有 个不相等的实数根;
②方程x2﹣2|x|=2有 个不相等的实数根;
③关于x的方程x2﹣2|x|=a有4个不相等的实数根时,a的取值范围是 .
18.有这样一个问题:探究函数y=x2+的图象与性质.
小东根据学习函数的经验,对函数y=x2+的图象与性质进行了探究.
下面是小东的探究过程,请补充完整:
(1)函数y=x2+的自变量x的取值范围是 ;
(2)下表是y与x的几组对应值.
x … ﹣3 ﹣2 ﹣1 ﹣ ﹣ 1 2 3 …
y … ﹣ ﹣ ﹣ m …
求m的值;
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
(4)进一步探究发现,该函数图象在第一象限内的最低点的坐标是(1,),结合函数的图象,写出该函数的其它性质(一条即可) .
19.在平面直角坐标系中,A(﹣1,0),B(3,0).
(1)若抛物线过A、B两点,且与y轴交于点(0,﹣3),求此抛物线的顶点坐标;
(2)如图,小敏发现所有过A、B两点的抛物线如果与y轴负半轴交于点C,M为抛物线的顶点,那么△ACM与△ACB的面积比不变,请你求出这个比值.
20.有这样一个问题:探究函数y=﹣2x的图象与性质.小彤根据学习函数的经验,对函数y=﹣2x的图象与性质进行了探究.下面是小彤探究的过程,请补充完整:
x .. ﹣4 ﹣3.5 ﹣3 ﹣2 ﹣1 0 1 2 3 3.5 4 …
y … ﹣ ﹣ 0 ﹣ ﹣ m
(1)求m的值为 ;
(2)如图,在平面直角坐标xOy中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出了图象的一部分,请根据剩余的点补全此函数的图象;
(3)方程﹣2x=﹣2实数根的个数为 ;
(4)观察图象,写出该函数的一条性质 ;
(5)在第(2)问的平面直角坐标系中画出直线y=x,根据图象写出方程x3﹣2x=x的一个正数根约为 (精确到0.1).
21.如图,抛物线y=﹣x2+bx+c过点A(4,0),B(﹣4,﹣4).
(1)求抛物线的解析式;
(2)若点P是线段AB上的一个动点(不与A、B重合),过P作y轴的平行线,分别交抛物线及x轴于C、D两点.请问是否存在这样的点P,使PD=2CD?若存在,请求出点P的坐标;若不存在,请说明理由.
22.某商店原来平均每天可销售某种水果100千克,每千克可盈利7元,为减少库存,经市场调查,如果这种水果每千克降价1元,则每天可所多售出20千克.
(1)设每千克水果降价x元,平均每天盈利y元,试写出y关于x的函数表达式;
(2)若要平均每天盈利400元,则每千克应降价多少元?
(3)每千克降价多少元时,每天的盈利最多?最多盈利多少元?
23.某瓜果基地市场部为指导该基地某种蔬菜的生产和销售,对往年的市场行情和生产情况进行了调查,提供了两个信息图,如甲、乙两图.(注:甲、乙两图中的A,B,C,D,E,F,G,H所对应的纵坐标分别指相应月份每千克该种蔬菜的售价和成本.生产成本6月份最低,甲图的图象是线段,乙图的图象是抛物线的一部分).请你根据图象提供的信息说明:
(1)在3月份出售这种蔬菜,每千克的收益是多少元?(收益=售价﹣成本)
(2)哪个月出售这种蔬菜,每千克的收益最大?说明理由.
24.在平面直角坐标系中,直线y=x﹣2与x轴交于点B,与y轴交于点C,二次函数y=x2+bx+c的图象经过B,C两点,且与x轴的负半轴交于点A.
(1)求二次函数的解析式;
(2)如图1,点M是线段BC上的一动点,动点D在直线BC下方的二次函数图象上.设点D的横坐标为m.
①过点D作DM⊥BC于点M,求线段DM关于m的函数关系式,并求线段DM的最大值;
②若△CDM为等腰直角三角形,直接写出点M的坐标.
25.如图,抛物线y=ax2+x+c交x轴于A,B两点,交y轴于点C.直线y=﹣x﹣2经过点A,C.
(1)求抛物线的解析式;
(2)点P是抛物线上一动点,过点P作x轴的垂线,交直线AC于点M,设点P的横坐标为m.
①当△PCM是直角三角形时,求点P的坐标;
②作点B关于点C的对称点B',则平面内存在直线l,使点M,B,B′到该直线的距离都相等.当点P在y轴右侧的抛物线上,且与点B不重合时,请直接写出直线l:y=kx+b的解析式.(k,b可用含m的式子表示)
参考答案
1.解:A、y=x2+,含有分式,故不是二次函数,故此选项错误;
B、y=2﹣x2,是二次函数,故此选项正确;
C、y=含有分式,故不是二次函数,故此选项错误;
D、y=(x﹣1)2﹣x2=﹣2x+1,是一次函数,故此选项错误.
故选:B.
2.解:A、根据函数的图象可知y随x的增大而增大,故本选项错误;
B、根据函数的图象可知在第二象限内y随x的增大而增大,故本选项错误;
C、根据函数的图象可知,当x<0时,在对称轴的右侧y随x的增大而减小,在对称轴的左侧y随x的增大而增大,故本选项错误;
D、根据函数的图象可知,当x<0时,y随x的增大而减小;故本选项正确.
故选:D.
3.解:∵y=4(x+1)(x﹣3)=4(x﹣1)2﹣16,
∴a=4>0,该抛物线的开口向上,故选项A错误,
与x轴的交点坐标是(﹣1,0)、(3,0),故选项B错误,
当x<1时,y随x的增大而减小,故选项C正确,
图象的对称轴是直线x=1,故选项D错误,
故选:C.
4.解:①∵抛物线开口向下,a<0,对称轴在y轴右侧,
∴b>0,①正确;
②x=﹣1时,y<0,
∴a﹣b+c<0,②正确;
③抛物线与直线y=1有两个交点,
∴ax2+bx+c=1有两个实数根,③正确;
故选:D.
5.解:设y=ax2+bx+5,
当x=1和x=3时,代数式ax2+bx+5的值相等,即当x=1和x=3时,函数值相等,
∴当x=0与x=4时,函数值相等,
∵当x=0时,y=5,
∴当x=4时,y=5,
故选:A.
6.解:将二次函数y=x2的图象向右平移1个单位,再向上平移2个单位后,所得图象的函数表达式是 y=(x﹣1)2+2,
故选:A.
7.解:根据二次函数的性质,当x=﹣1时,二次函数y=(x﹣1)2﹣2的最小值是﹣2.
故选:D.
8.解:∵二次函数y=ax2+bx+c的顶点为(1,﹣4),
∴对称轴为x=1,
而对称轴左侧图象与x轴交点横坐标的取值范围是﹣3<x<﹣2,
∴右侧交点横坐标的取值范围是4<x<5.
故选:C.
9.解:根据图象可知:
当x<﹣1时,y1<y2,
当x=﹣1时,y1=y2,
当﹣1<x<2时,y1>y2,
当x=2时,y1=y2,
当x>2时,y1<y2,
故选:A.
10.解:∵长方形的周长为24cm,其中一边为x(其中x>0),
∴长方形的另一边长为12﹣x,
∴y=(12﹣x) x.
故选:C.
11.解:
由图象开口向下,可知a<0,
与y轴的交点在x轴的下方,可知c<0,
又对称轴方程为x=2,所以﹣>0,所以b>0,
∴abc>0,故①正确;
由图象可知当x=3时,y>0,
∴9a+3b+c>0,故②错误;
由图象可知OA<1,
∵OA=OC,
∴OC<1,即﹣c<1,
∴c>﹣1,故③正确;
假设方程的一个根为x=﹣,把x=﹣代入方程可得﹣+c=0,
整理可得ac﹣b+1=0,
两边同时乘c可得ac2﹣bc+c=0,
即方程有一个根为x=﹣c,
由②可知﹣c=OA,而当x=OA是方程的根,
∴x=﹣c是方程的根,即假设成立,故④正确;
综上可知正确的结论有三个,
故选:C.
12.解:由二次函数的定义可知,当时,该函数是二次函数
∴
∴m=1
故答案为:1.
13.解:∵点P在函数y=﹣上,点P的纵坐标为1,
∴1=,
解得x=﹣3,
∴函数y=﹣与y=ax2+bx(a>0,b>0)的图象交于点P的坐标为(﹣3,1),
∴
可得,,
∴,
解得x=﹣3.
故答案为:x=﹣3.
14.解:∵y=(x﹣m)2+3,
∴对称轴为x=m,
∵a=1>0,
∴抛物线开口向上,
∴在对称轴右侧y随x的增大而增大,
∵当x>1时,y随x的增大而增大,
∴m≤1,
故答案为:m≤1.
15.解:将抛物线y=﹣2x2向下平移2个单位长度,得到的抛物线的解析式是:y=﹣2x2﹣2,
再向左平移1个单位长度,得到的抛物线的解析式是:y=﹣2(x+1)2﹣2.
故答案是:y=﹣2(x+1)2﹣2.
16.解:(1)由题意x≠0,m=,
故答案为x≠0,.
(2)函数图象如图所示.
(3)①由图象可知与x轴有一个交点,对应方程x2+=0有一个实数根.
故答案为1,1.
②观察图象可知,方程x2+=2有3个实数根,
故答案为3.
③在函数没有最大值或这个函数没有最小值,函数图象没有经过第四象限等,答案不唯一.
故答案为函数没有最大值或这个函数没有最小值,函数图象没有经过第四象限
17.解:(1)把x=﹣2代入y=x2﹣2|x|得y=0,
即m=0,
故答案为:0;
(2)如图所示;
(3)由函数图象知:①函数y=x2﹣2|x|的图象关于y轴对称;②当x>1时,y随x的增大而增大;
(4)①由函数图象知:函数图象与x轴有3个交点,所以对应的方程x2﹣2|x|=0有3个不相等的实数根;
②如图,∵y=x2﹣2|x|的图象与直线y=2有两个交点,
∴x2﹣2|x|=2有2个不相等的实数根;
③由函数图象知:∵关于x的方程x2﹣2|x|=a有4个不相等的实数根,
∴a的取值范围是﹣1<a<0,
故答案为:3,3,2,﹣1<a<0.
18.解:(1)x≠0,
(2)令x=3,
∴y=×32+
=+=;
∴m=;
(3)如图
(4)该函数的其它性质:
①该函数没有最大值;
②该函数在x=0处断开;
③该函数没有最小值;
④该函数图象没有经过第四象限.
故答案为该函数没有最大值.
19.解:(1)设过抛物线A,B两点,且与y轴交于点(0,﹣3),的抛物线解析式为y=ax2+bx+c,
把A(﹣1,0),B(3,0),点(0,﹣3)代入
得,
解得,
故此抛物线的解析式为y=x2﹣2x﹣3,顶点坐标为(1,﹣4);
(2)由题意,设y=a(x+1)(x﹣3),即y=ax2﹣2ax﹣3a,
∴A(﹣1,0),B(3,0),C(0,﹣3a),M(1,﹣4a),
∴S△ACB=×4×|﹣3a|=6|a|,
而a>0,
∴S△ACB=6a.
作MD⊥x轴于D,
又S△ACM=S△ACO+SOCMD﹣S△AMD= 1 3a+(3a+4a)﹣ 2 4a=a,
∴S△ACM:S△ACB=1:6;
20.解:(1)当x=3时,y=﹣2x=×27﹣2×3=﹣,即m=﹣;
(2)如图所示;
(3)方程﹣2x=﹣2实数根的个数为3个;
(4)图象关于原点中心对称或x>2时,y随x的增大而增大等(答案不唯一)
(5)如图,直线y=x与函数y=﹣2x的图象在第一象限内的交点的横坐标约为3.9,
所以方程x3﹣2x=x的一个正数根约为3.9.
故答案为﹣;3;x>2时,y随x的增大而增大等;3.9.
21.解:(1)由题意,解得,
∴抛物线的解析式为y=﹣x2+x+2.
(2)∵A(4,0),B(﹣4,﹣4),
∴直线AB的解析式为y=x﹣2,
设P(m,m﹣2),其中﹣4<m<4,则C(m,﹣m2+m+2),PD=2﹣m,CD=|﹣m2+m+2|,
①当点C在x轴上方时,CD=﹣m2+m+2,由PD=2CD,
得2﹣m=2(﹣m2+m+2),解得m=﹣1或4(舍弃),
∴P(﹣1,﹣).
②当点C在x轴下方时,CD=m2﹣m﹣2,由PD=2CD,得2﹣m=2(m2﹣m﹣2),解得m=﹣3或4(舍弃),
∴P(﹣3,﹣),
综上所述,点P的坐标为(﹣1,﹣)或(﹣3,﹣).
22.解:(1)根据题意得:
y=(100+20x)×(7﹣x)
=﹣20x2+40x+700;
(2)令y=﹣20x2+40x+700中y=400,则有:400=﹣20x2+40x+700,
即x2﹣2x﹣15=0,
解得:x1=﹣3(舍去),x2=5.
所以若要平均每天盈利400元,则每千克应降价5元.
(3)y=﹣20x2+40x+700=﹣20(x﹣1)2+720,
所以每千克降价1元时,每天的盈利最多,最多盈利720元.
23.解:(1)从甲图知:3月份出售这种蔬菜,每千克售价为5元;
从乙图知,3月份购买这种蔬菜的成本为每千克4元,
根据收益=售价﹣成本,易知,
在3月份出售这种蔬菜每千克的收益是1元;
(2)设图甲中图象的函数关系为y甲=kx+b,图乙中图象的函数关系式为y乙=a(x﹣h)2+k,
则每千克收益为y=y甲﹣y乙(元),
∴,
解得:,
∴y甲=﹣x+7,
∴抛物线y乙=a(x﹣h)2+k.的顶点坐标为(6,1),又过点(3,4),
∴y乙=a(x﹣6)2+1,
∴4=a(3﹣6)2+1,∴a=,
∴y乙=(x﹣6)2+1,
∴y=y甲﹣y乙=﹣x+7﹣(x﹣6)2﹣1,
y=﹣(x﹣5)2+,
∴当x=5时,y有最大值.即当5月份出售时,每千克收益最大.
24.解(1)由直线y=x﹣2得
B(4,0)、C(0,﹣2),
将B(4,0)、C(0,﹣2)代入y=x2+bx+c,
,
解得b=,c=﹣2,
∴二次函数的解析式y=x2﹣x﹣2;
(2)①过点DH∥AB,交直线y=x﹣2于点H.
∴∠H=∠OBC,
∵B(4,0)、C(0,﹣2),
∴OC=2,OB=4,BC=2
∴sin∠H=sin∠OBC===,
即=,
设D(m,m2﹣m﹣2),则H(m2﹣3m,m2﹣m﹣2),
∴DH=m﹣(m2﹣3m)=﹣m2+4m,
∴DM=(﹣m2+4m)=﹣,
当m=2时,DM的最大值为;
②Ⅰ.当CM⊥DM时,过点M作ME⊥y轴于点E,点D作DF∥y轴,交EM的延长线于点F,
∵△CDM为等腰直角三角形,易证△EMC≌△FDM,
∴EM=DF,EC=MF,
设M(t,t﹣2),则EM=t,OE=﹣t+2,
∴CE=OC﹣OE=2﹣(﹣t+2)=t,MF=t,DF=t,
EF=EM+MF=t+t=,OE+DF=﹣t+2+t=t+2,
∴D(t,﹣t﹣2)
将D(t,﹣t﹣2)代入二次函数的解析式y=x2﹣x﹣2,
,
解得t=0(舍去)或t=,
∴M1();
Ⅱ.当CD⊥DM时,过点D作DE⊥y轴于点E,点M作MF∥y轴,交ED的延长线于点F,
∵△CDM为等腰直角三角形,易证△CED≌△DFM,
∴DE=MF,EC=DF,
设M(t,t﹣2),则EF=t,DF=CE=,DE=t,MF=t,OE=t+2
∴D(t,﹣t﹣2),
将D(t,﹣t﹣2)代入二次函数的解析式y=x2﹣x﹣2,
,
解得t=0(舍去)或t=,
∴M2(,﹣)
综上,△CDM为等腰直角三角形,点M的坐标为M1()或M2(,﹣)
25.解:(1)当x=0时,y=﹣x﹣2=﹣2,
∴点C的坐标为(0,﹣2);
当y=0时,﹣x﹣2=0,
解得:x=﹣4,
∴点A的坐标为(﹣4,0).
将A(﹣4,0),C(0,﹣2)代入y=ax2+x+c,得:
,解得:,
∴抛物线的解析式为y=x2+x﹣2.
(2)①∵PM⊥x轴,
∴∠PMC≠90°,
∴分两种情况考虑,如图1所示.
(i)当∠MPC=90°时,PC∥x轴,
∴点P的纵坐标为﹣2.
当y=﹣2时,x2+x﹣2=﹣2,
解得:x1=﹣2,x2=0,
∴点P的坐标为(﹣2,﹣2);
(ii)当∠PCM=90°时,设PC与x轴交于点D.
∵∠OAC+∠OCA=90°,∠OCA+∠OCD=90°,
∴∠OAC=∠OCD.
又∵∠AOC=∠COD=90°,
∴△AOC∽△COD,
∴=,即=,
∴OD=1,
∴点D的坐标为(1,0).
设直线PC的解析式为y=kx+b(k≠0),
将C(0,﹣2),D(1,0)代入y=kx+b,得:
,解得:,
∴直线PC的解析式为y=2x﹣2.
联立直线PC和抛物线的解析式成方程组,得:,
解得:,,
点P的坐标为(6,10).
综上所述:当△PCM是直角三角形时,点P的坐标为(﹣2,﹣2)或(6,10).
②当y=0时,x2+x﹣2=0,
解得:x1=﹣4,x2=2,
∴点B的坐标为(2,0).
∵点C的坐标为(0,﹣2),点B,B′关于点C对称,
∴点B′的坐标为(﹣2,﹣4).
∵点P的横坐标为m(m>0且m≠2),
∴点M的坐标为(m,﹣m﹣2).
利用待定系数法可求出:直线BM的解析式为y=﹣x+,直线B′M的解析式为y=x﹣,直线BB′的解析式为y=x﹣2.
分三种情况考虑,如图2所示:
当直线l∥BM且过点C时,直线l的解析式为y=﹣x﹣2;
当直线l∥B′M且过点C时,直线l的解析式为y=x﹣2;
当直线l∥BB′且过线段CM的中点N(m,﹣m﹣2)时,直线l的解析式为y=x﹣m﹣2.
综上所述:直线l的解析式为y=﹣x﹣2,y=x﹣2或y=x﹣m﹣2.
1.下列各式中表示二次函数的是( )
A.y=x2+ B.y=2﹣x2
C.y= D.y=(x﹣1)2﹣x2
2.下列四个函数图象中,当x<0时,函数值y随自变量x的增大而减小的是( )
A.B.C.D.
3.对于二次函数y=4(x+1)(x﹣3)下列说法正确的是( )
A.图象开口向下 B.与x轴交点坐标是(1,0)和(﹣3,0)
C.x<1时,y随x的增大而减小 D.图象的对称轴是直线x=﹣1
4.如图,已知二次函数y=ax2+bx+c(a≠0)的图象.下列结论:①b>0;②a﹣b+c<0;③ax2+bx+c=1有两个实数根.其中正确的个数是( )
A.0 B.1 C.2 D.3
5.若当x=1和x=3时,代数式ax2+bx+5的值相等,则当x=4时,代数式ax2+bx+5的值是( )
A.5 B.﹣5 C.0 D.2
6.将二次函数y=x2的图象向右平移1个单位,再向上平移2个单位后,所得图象的函数表达式是( )
A.y=(x﹣1)2+2 B.y=(x+1)2+2 C.y=(x﹣1)2﹣2 D.y=(x+1)2﹣2
7.函数y=(x+1)2﹣2的最小值是( )
A.1 B.﹣1 C.2 D.﹣2
8.如图,以(1,﹣4)为顶点的二次函数y=ax2+bx+c的图象与x轴负半轴交于A点,则一元二次方程ax2+bx+c=0的正数解的范围是( )
A.2<x<3 B.3<x<4 C.4<x<5 D.5<x<6
9.如图,直线y1=kx+n(k≠0)与抛物线y2=ax2+bx+c(a≠0)分别交于A(﹣1,0),B(2,﹣3)两点,那么当y1>y2时,x的取值范围是( )
A.﹣1<x<2 B.x>2 C.x<﹣1或x>2 D.x≤﹣1
10.长方形的周长为24cm,其中一边长为xcm(其中x>0),面积为ycm2,则这样的长方形中y与x的关系可以写为( )
A.y=x2 B.y=12﹣x2 C.y=(12﹣x) x D.y=2(12﹣x)
11.如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴正半轴相交于A、B两点,与y轴相交于点C,对称轴为直线x=2,且OA=OC,则下列结论:
①abc>0;②9a+3b+c<0;③c>﹣1;④关于x的方程ax2+bx+c=0(a≠0)有一个根为﹣
其中正确的结论个数有( )
A.1个 B.2个 C.3个 D.4个
12.函数y=(m+1)x|m|+1+5x﹣5是二次函数,则m= .
13.如图,已知函数y=﹣与y=ax2+bx(a>0,b>0)的图象交于点P,点P的纵坐标为1,则关于x的方程ax2+bx+=0的解是 .
14.已知抛物线y=(x﹣m)2+3,当x>1时,y随x的增大而增大,则m的取值范围是 .
15.在平面直角坐标系中,把抛物线y=﹣2x2向下平移2个单位长度,再向左平移1个单位长度,得到的新抛物线解析式为 .
16.有这样一个问题:探究函数y=x2+的图象与性质,小东根据学习函数的经验,对函数y=x2+的图象与性质进行了探究,下面是小东的探究过程,请补充完整:
(1)下表是y与x的几组对应值.
x … ﹣3 ﹣2 ﹣1 1 2 3 …
y … ﹣ m …
函数y=x2+的自变量x的取值范围是 ,m的值为 ;
(2)在如图所示的平面直角坐标系xOy中,描出以上表中各对对应值为坐标的点.并画出该函数的大致图象;
(3)进一步探究函数图象发现:
①函数图象与x轴有 个交点,所以对应方程x2+=0有 个实数根;
②方程x2+=2有 个实数根;
③结合函数的图象,写出该函数的一条性质 .
17.某班“数学兴趣小组”对函数y=x2﹣2|x|的图象和性质进行了探究,探究过程如下,请补充完整.
(1)自变量x的取值范围是全体实数,x与y的几组对应值列表如下:
x … ﹣3 ﹣ ﹣2 ﹣1 0 1 2 3 …
y … 3 m ﹣1 0 ﹣1 0 3 …
其中,m= .
(2)根据表中数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请画出该函数图象的另一部分.
(3)观察函数图象,写出两条函数的性质.
(4)进一步探究函数图象发现:
①函数图象与x轴有 个交点,所以对应的方程x2﹣2|x|=0有 个不相等的实数根;
②方程x2﹣2|x|=2有 个不相等的实数根;
③关于x的方程x2﹣2|x|=a有4个不相等的实数根时,a的取值范围是 .
18.有这样一个问题:探究函数y=x2+的图象与性质.
小东根据学习函数的经验,对函数y=x2+的图象与性质进行了探究.
下面是小东的探究过程,请补充完整:
(1)函数y=x2+的自变量x的取值范围是 ;
(2)下表是y与x的几组对应值.
x … ﹣3 ﹣2 ﹣1 ﹣ ﹣ 1 2 3 …
y … ﹣ ﹣ ﹣ m …
求m的值;
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
(4)进一步探究发现,该函数图象在第一象限内的最低点的坐标是(1,),结合函数的图象,写出该函数的其它性质(一条即可) .
19.在平面直角坐标系中,A(﹣1,0),B(3,0).
(1)若抛物线过A、B两点,且与y轴交于点(0,﹣3),求此抛物线的顶点坐标;
(2)如图,小敏发现所有过A、B两点的抛物线如果与y轴负半轴交于点C,M为抛物线的顶点,那么△ACM与△ACB的面积比不变,请你求出这个比值.
20.有这样一个问题:探究函数y=﹣2x的图象与性质.小彤根据学习函数的经验,对函数y=﹣2x的图象与性质进行了探究.下面是小彤探究的过程,请补充完整:
x .. ﹣4 ﹣3.5 ﹣3 ﹣2 ﹣1 0 1 2 3 3.5 4 …
y … ﹣ ﹣ 0 ﹣ ﹣ m
(1)求m的值为 ;
(2)如图,在平面直角坐标xOy中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出了图象的一部分,请根据剩余的点补全此函数的图象;
(3)方程﹣2x=﹣2实数根的个数为 ;
(4)观察图象,写出该函数的一条性质 ;
(5)在第(2)问的平面直角坐标系中画出直线y=x,根据图象写出方程x3﹣2x=x的一个正数根约为 (精确到0.1).
21.如图,抛物线y=﹣x2+bx+c过点A(4,0),B(﹣4,﹣4).
(1)求抛物线的解析式;
(2)若点P是线段AB上的一个动点(不与A、B重合),过P作y轴的平行线,分别交抛物线及x轴于C、D两点.请问是否存在这样的点P,使PD=2CD?若存在,请求出点P的坐标;若不存在,请说明理由.
22.某商店原来平均每天可销售某种水果100千克,每千克可盈利7元,为减少库存,经市场调查,如果这种水果每千克降价1元,则每天可所多售出20千克.
(1)设每千克水果降价x元,平均每天盈利y元,试写出y关于x的函数表达式;
(2)若要平均每天盈利400元,则每千克应降价多少元?
(3)每千克降价多少元时,每天的盈利最多?最多盈利多少元?
23.某瓜果基地市场部为指导该基地某种蔬菜的生产和销售,对往年的市场行情和生产情况进行了调查,提供了两个信息图,如甲、乙两图.(注:甲、乙两图中的A,B,C,D,E,F,G,H所对应的纵坐标分别指相应月份每千克该种蔬菜的售价和成本.生产成本6月份最低,甲图的图象是线段,乙图的图象是抛物线的一部分).请你根据图象提供的信息说明:
(1)在3月份出售这种蔬菜,每千克的收益是多少元?(收益=售价﹣成本)
(2)哪个月出售这种蔬菜,每千克的收益最大?说明理由.
24.在平面直角坐标系中,直线y=x﹣2与x轴交于点B,与y轴交于点C,二次函数y=x2+bx+c的图象经过B,C两点,且与x轴的负半轴交于点A.
(1)求二次函数的解析式;
(2)如图1,点M是线段BC上的一动点,动点D在直线BC下方的二次函数图象上.设点D的横坐标为m.
①过点D作DM⊥BC于点M,求线段DM关于m的函数关系式,并求线段DM的最大值;
②若△CDM为等腰直角三角形,直接写出点M的坐标.
25.如图,抛物线y=ax2+x+c交x轴于A,B两点,交y轴于点C.直线y=﹣x﹣2经过点A,C.
(1)求抛物线的解析式;
(2)点P是抛物线上一动点,过点P作x轴的垂线,交直线AC于点M,设点P的横坐标为m.
①当△PCM是直角三角形时,求点P的坐标;
②作点B关于点C的对称点B',则平面内存在直线l,使点M,B,B′到该直线的距离都相等.当点P在y轴右侧的抛物线上,且与点B不重合时,请直接写出直线l:y=kx+b的解析式.(k,b可用含m的式子表示)
参考答案
1.解:A、y=x2+,含有分式,故不是二次函数,故此选项错误;
B、y=2﹣x2,是二次函数,故此选项正确;
C、y=含有分式,故不是二次函数,故此选项错误;
D、y=(x﹣1)2﹣x2=﹣2x+1,是一次函数,故此选项错误.
故选:B.
2.解:A、根据函数的图象可知y随x的增大而增大,故本选项错误;
B、根据函数的图象可知在第二象限内y随x的增大而增大,故本选项错误;
C、根据函数的图象可知,当x<0时,在对称轴的右侧y随x的增大而减小,在对称轴的左侧y随x的增大而增大,故本选项错误;
D、根据函数的图象可知,当x<0时,y随x的增大而减小;故本选项正确.
故选:D.
3.解:∵y=4(x+1)(x﹣3)=4(x﹣1)2﹣16,
∴a=4>0,该抛物线的开口向上,故选项A错误,
与x轴的交点坐标是(﹣1,0)、(3,0),故选项B错误,
当x<1时,y随x的增大而减小,故选项C正确,
图象的对称轴是直线x=1,故选项D错误,
故选:C.
4.解:①∵抛物线开口向下,a<0,对称轴在y轴右侧,
∴b>0,①正确;
②x=﹣1时,y<0,
∴a﹣b+c<0,②正确;
③抛物线与直线y=1有两个交点,
∴ax2+bx+c=1有两个实数根,③正确;
故选:D.
5.解:设y=ax2+bx+5,
当x=1和x=3时,代数式ax2+bx+5的值相等,即当x=1和x=3时,函数值相等,
∴当x=0与x=4时,函数值相等,
∵当x=0时,y=5,
∴当x=4时,y=5,
故选:A.
6.解:将二次函数y=x2的图象向右平移1个单位,再向上平移2个单位后,所得图象的函数表达式是 y=(x﹣1)2+2,
故选:A.
7.解:根据二次函数的性质,当x=﹣1时,二次函数y=(x﹣1)2﹣2的最小值是﹣2.
故选:D.
8.解:∵二次函数y=ax2+bx+c的顶点为(1,﹣4),
∴对称轴为x=1,
而对称轴左侧图象与x轴交点横坐标的取值范围是﹣3<x<﹣2,
∴右侧交点横坐标的取值范围是4<x<5.
故选:C.
9.解:根据图象可知:
当x<﹣1时,y1<y2,
当x=﹣1时,y1=y2,
当﹣1<x<2时,y1>y2,
当x=2时,y1=y2,
当x>2时,y1<y2,
故选:A.
10.解:∵长方形的周长为24cm,其中一边为x(其中x>0),
∴长方形的另一边长为12﹣x,
∴y=(12﹣x) x.
故选:C.
11.解:
由图象开口向下,可知a<0,
与y轴的交点在x轴的下方,可知c<0,
又对称轴方程为x=2,所以﹣>0,所以b>0,
∴abc>0,故①正确;
由图象可知当x=3时,y>0,
∴9a+3b+c>0,故②错误;
由图象可知OA<1,
∵OA=OC,
∴OC<1,即﹣c<1,
∴c>﹣1,故③正确;
假设方程的一个根为x=﹣,把x=﹣代入方程可得﹣+c=0,
整理可得ac﹣b+1=0,
两边同时乘c可得ac2﹣bc+c=0,
即方程有一个根为x=﹣c,
由②可知﹣c=OA,而当x=OA是方程的根,
∴x=﹣c是方程的根,即假设成立,故④正确;
综上可知正确的结论有三个,
故选:C.
12.解:由二次函数的定义可知,当时,该函数是二次函数
∴
∴m=1
故答案为:1.
13.解:∵点P在函数y=﹣上,点P的纵坐标为1,
∴1=,
解得x=﹣3,
∴函数y=﹣与y=ax2+bx(a>0,b>0)的图象交于点P的坐标为(﹣3,1),
∴
可得,,
∴,
解得x=﹣3.
故答案为:x=﹣3.
14.解:∵y=(x﹣m)2+3,
∴对称轴为x=m,
∵a=1>0,
∴抛物线开口向上,
∴在对称轴右侧y随x的增大而增大,
∵当x>1时,y随x的增大而增大,
∴m≤1,
故答案为:m≤1.
15.解:将抛物线y=﹣2x2向下平移2个单位长度,得到的抛物线的解析式是:y=﹣2x2﹣2,
再向左平移1个单位长度,得到的抛物线的解析式是:y=﹣2(x+1)2﹣2.
故答案是:y=﹣2(x+1)2﹣2.
16.解:(1)由题意x≠0,m=,
故答案为x≠0,.
(2)函数图象如图所示.
(3)①由图象可知与x轴有一个交点,对应方程x2+=0有一个实数根.
故答案为1,1.
②观察图象可知,方程x2+=2有3个实数根,
故答案为3.
③在函数没有最大值或这个函数没有最小值,函数图象没有经过第四象限等,答案不唯一.
故答案为函数没有最大值或这个函数没有最小值,函数图象没有经过第四象限
17.解:(1)把x=﹣2代入y=x2﹣2|x|得y=0,
即m=0,
故答案为:0;
(2)如图所示;
(3)由函数图象知:①函数y=x2﹣2|x|的图象关于y轴对称;②当x>1时,y随x的增大而增大;
(4)①由函数图象知:函数图象与x轴有3个交点,所以对应的方程x2﹣2|x|=0有3个不相等的实数根;
②如图,∵y=x2﹣2|x|的图象与直线y=2有两个交点,
∴x2﹣2|x|=2有2个不相等的实数根;
③由函数图象知:∵关于x的方程x2﹣2|x|=a有4个不相等的实数根,
∴a的取值范围是﹣1<a<0,
故答案为:3,3,2,﹣1<a<0.
18.解:(1)x≠0,
(2)令x=3,
∴y=×32+
=+=;
∴m=;
(3)如图
(4)该函数的其它性质:
①该函数没有最大值;
②该函数在x=0处断开;
③该函数没有最小值;
④该函数图象没有经过第四象限.
故答案为该函数没有最大值.
19.解:(1)设过抛物线A,B两点,且与y轴交于点(0,﹣3),的抛物线解析式为y=ax2+bx+c,
把A(﹣1,0),B(3,0),点(0,﹣3)代入
得,
解得,
故此抛物线的解析式为y=x2﹣2x﹣3,顶点坐标为(1,﹣4);
(2)由题意,设y=a(x+1)(x﹣3),即y=ax2﹣2ax﹣3a,
∴A(﹣1,0),B(3,0),C(0,﹣3a),M(1,﹣4a),
∴S△ACB=×4×|﹣3a|=6|a|,
而a>0,
∴S△ACB=6a.
作MD⊥x轴于D,
又S△ACM=S△ACO+SOCMD﹣S△AMD= 1 3a+(3a+4a)﹣ 2 4a=a,
∴S△ACM:S△ACB=1:6;
20.解:(1)当x=3时,y=﹣2x=×27﹣2×3=﹣,即m=﹣;
(2)如图所示;
(3)方程﹣2x=﹣2实数根的个数为3个;
(4)图象关于原点中心对称或x>2时,y随x的增大而增大等(答案不唯一)
(5)如图,直线y=x与函数y=﹣2x的图象在第一象限内的交点的横坐标约为3.9,
所以方程x3﹣2x=x的一个正数根约为3.9.
故答案为﹣;3;x>2时,y随x的增大而增大等;3.9.
21.解:(1)由题意,解得,
∴抛物线的解析式为y=﹣x2+x+2.
(2)∵A(4,0),B(﹣4,﹣4),
∴直线AB的解析式为y=x﹣2,
设P(m,m﹣2),其中﹣4<m<4,则C(m,﹣m2+m+2),PD=2﹣m,CD=|﹣m2+m+2|,
①当点C在x轴上方时,CD=﹣m2+m+2,由PD=2CD,
得2﹣m=2(﹣m2+m+2),解得m=﹣1或4(舍弃),
∴P(﹣1,﹣).
②当点C在x轴下方时,CD=m2﹣m﹣2,由PD=2CD,得2﹣m=2(m2﹣m﹣2),解得m=﹣3或4(舍弃),
∴P(﹣3,﹣),
综上所述,点P的坐标为(﹣1,﹣)或(﹣3,﹣).
22.解:(1)根据题意得:
y=(100+20x)×(7﹣x)
=﹣20x2+40x+700;
(2)令y=﹣20x2+40x+700中y=400,则有:400=﹣20x2+40x+700,
即x2﹣2x﹣15=0,
解得:x1=﹣3(舍去),x2=5.
所以若要平均每天盈利400元,则每千克应降价5元.
(3)y=﹣20x2+40x+700=﹣20(x﹣1)2+720,
所以每千克降价1元时,每天的盈利最多,最多盈利720元.
23.解:(1)从甲图知:3月份出售这种蔬菜,每千克售价为5元;
从乙图知,3月份购买这种蔬菜的成本为每千克4元,
根据收益=售价﹣成本,易知,
在3月份出售这种蔬菜每千克的收益是1元;
(2)设图甲中图象的函数关系为y甲=kx+b,图乙中图象的函数关系式为y乙=a(x﹣h)2+k,
则每千克收益为y=y甲﹣y乙(元),
∴,
解得:,
∴y甲=﹣x+7,
∴抛物线y乙=a(x﹣h)2+k.的顶点坐标为(6,1),又过点(3,4),
∴y乙=a(x﹣6)2+1,
∴4=a(3﹣6)2+1,∴a=,
∴y乙=(x﹣6)2+1,
∴y=y甲﹣y乙=﹣x+7﹣(x﹣6)2﹣1,
y=﹣(x﹣5)2+,
∴当x=5时,y有最大值.即当5月份出售时,每千克收益最大.
24.解(1)由直线y=x﹣2得
B(4,0)、C(0,﹣2),
将B(4,0)、C(0,﹣2)代入y=x2+bx+c,
,
解得b=,c=﹣2,
∴二次函数的解析式y=x2﹣x﹣2;
(2)①过点DH∥AB,交直线y=x﹣2于点H.
∴∠H=∠OBC,
∵B(4,0)、C(0,﹣2),
∴OC=2,OB=4,BC=2
∴sin∠H=sin∠OBC===,
即=,
设D(m,m2﹣m﹣2),则H(m2﹣3m,m2﹣m﹣2),
∴DH=m﹣(m2﹣3m)=﹣m2+4m,
∴DM=(﹣m2+4m)=﹣,
当m=2时,DM的最大值为;
②Ⅰ.当CM⊥DM时,过点M作ME⊥y轴于点E,点D作DF∥y轴,交EM的延长线于点F,
∵△CDM为等腰直角三角形,易证△EMC≌△FDM,
∴EM=DF,EC=MF,
设M(t,t﹣2),则EM=t,OE=﹣t+2,
∴CE=OC﹣OE=2﹣(﹣t+2)=t,MF=t,DF=t,
EF=EM+MF=t+t=,OE+DF=﹣t+2+t=t+2,
∴D(t,﹣t﹣2)
将D(t,﹣t﹣2)代入二次函数的解析式y=x2﹣x﹣2,
,
解得t=0(舍去)或t=,
∴M1();
Ⅱ.当CD⊥DM时,过点D作DE⊥y轴于点E,点M作MF∥y轴,交ED的延长线于点F,
∵△CDM为等腰直角三角形,易证△CED≌△DFM,
∴DE=MF,EC=DF,
设M(t,t﹣2),则EF=t,DF=CE=,DE=t,MF=t,OE=t+2
∴D(t,﹣t﹣2),
将D(t,﹣t﹣2)代入二次函数的解析式y=x2﹣x﹣2,
,
解得t=0(舍去)或t=,
∴M2(,﹣)
综上,△CDM为等腰直角三角形,点M的坐标为M1()或M2(,﹣)
25.解:(1)当x=0时,y=﹣x﹣2=﹣2,
∴点C的坐标为(0,﹣2);
当y=0时,﹣x﹣2=0,
解得:x=﹣4,
∴点A的坐标为(﹣4,0).
将A(﹣4,0),C(0,﹣2)代入y=ax2+x+c,得:
,解得:,
∴抛物线的解析式为y=x2+x﹣2.
(2)①∵PM⊥x轴,
∴∠PMC≠90°,
∴分两种情况考虑,如图1所示.
(i)当∠MPC=90°时,PC∥x轴,
∴点P的纵坐标为﹣2.
当y=﹣2时,x2+x﹣2=﹣2,
解得:x1=﹣2,x2=0,
∴点P的坐标为(﹣2,﹣2);
(ii)当∠PCM=90°时,设PC与x轴交于点D.
∵∠OAC+∠OCA=90°,∠OCA+∠OCD=90°,
∴∠OAC=∠OCD.
又∵∠AOC=∠COD=90°,
∴△AOC∽△COD,
∴=,即=,
∴OD=1,
∴点D的坐标为(1,0).
设直线PC的解析式为y=kx+b(k≠0),
将C(0,﹣2),D(1,0)代入y=kx+b,得:
,解得:,
∴直线PC的解析式为y=2x﹣2.
联立直线PC和抛物线的解析式成方程组,得:,
解得:,,
点P的坐标为(6,10).
综上所述:当△PCM是直角三角形时,点P的坐标为(﹣2,﹣2)或(6,10).
②当y=0时,x2+x﹣2=0,
解得:x1=﹣4,x2=2,
∴点B的坐标为(2,0).
∵点C的坐标为(0,﹣2),点B,B′关于点C对称,
∴点B′的坐标为(﹣2,﹣4).
∵点P的横坐标为m(m>0且m≠2),
∴点M的坐标为(m,﹣m﹣2).
利用待定系数法可求出:直线BM的解析式为y=﹣x+,直线B′M的解析式为y=x﹣,直线BB′的解析式为y=x﹣2.
分三种情况考虑,如图2所示:
当直线l∥BM且过点C时,直线l的解析式为y=﹣x﹣2;
当直线l∥B′M且过点C时,直线l的解析式为y=x﹣2;
当直线l∥BB′且过线段CM的中点N(m,﹣m﹣2)时,直线l的解析式为y=x﹣m﹣2.
综上所述:直线l的解析式为y=﹣x﹣2,y=x﹣2或y=x﹣m﹣2.
