苏科版九年级数学上册 第2章对称图形-圆数学活动 图形的密铺课件((共38张PPT))
文档属性
| 名称 | 苏科版九年级数学上册 第2章对称图形-圆数学活动 图形的密铺课件((共38张PPT)) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-28 00:00:00 | ||
图片预览









文档简介
(共38张PPT)
数学活动 图形的密铺
音乐能激发或抚慰情怀,绘画使人赏心悦目,诗歌能动人心弦,哲学使人获得智慧,科学可改善物质生活,但数学能给予以上的一切。
宇宙之大 粒子之微
火箭之速 化工之巧
地球之变 生物之谜
日用之繁 数学无处不在
——华罗庚
【问题导学】
活动一、自主先学 感悟新知
请欣赏视频中展示的各种拼铺图案,感受平面图形在生活中的广泛应用.
用图案密铺
版画设计
埃舍尔的密铺图形:
http://www./luo/mei.htm
平面图形的
密铺
用形状相同或不同的平面图形进行拼接,彼此之间既无空隙、又不重叠地铺成一片,就是平面图形的密铺, 也叫做平面图形的镶嵌.
活动二、合作交流 探索新知
1.快速抢答:
(1)n边形的内角和是 °,外角和是 °;
(2)各边相等、各角相等的多边形叫做 ;
(3)正三角形的每个内角是 °, 正五边形每个内角是 °, 正n边形每个内角是 °.
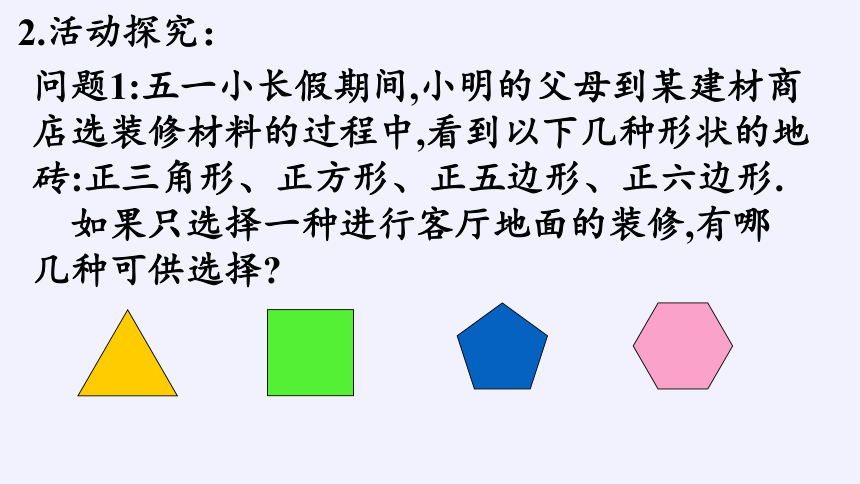
2.活动探究:
问题1:五一小长假期间,小明的父母到某建材商
店选装修材料的过程中,看到以下几种形状的地
砖:正三角形、正方形、正五边形、正六边形.
如果只选择一种进行客厅地面的装修,有哪
几种可供选择
活动要求:
小组合作探究,观察实验现象、思考原理、做好记录,尝试完成活动报告1.
思考:
(1)进行密铺时,同一拼接点处,所用的正多
边形各有几个?
(2)多边形能够密铺的条件是什么?一种正多
边形能够密铺的条件是什么?
结论:用同一种可以进行密铺的正多边形有
正三角形、正四边形、正六边形.
密铺的条件:
同一拼接点处,各角之和组成一个 3600 的周角.
问题2:用形状、大小完全相同的任意三角形能
密铺成平面图案吗?任意四边形呢?其它多边形
呢?
活动要求:小组合作探究,观察实验现象、思考
原理、做好记录,尝试完成活动报告2.
思考:
(1)进行密铺时,同一拼接点处,所用的任意多
边形各有几个?
(2)进行密铺时,应注意什么?
结论:形状、大小完全相同的任意三角形、四边形能
够密铺.
① 用同一种任意三角形
等腰三角形
直角三角形
任意三角形
② 用同一种任意四边形
③用其它特殊的多边形
五边形
六边形
问题3:小明的父母打算用边长相等的正三角形、
正方形、正五边形、正六边形中的两种地砖进
行厨房地面的装修,有哪些组合方式?
1.正三角形和正方形可以组合密铺,在同一拼接
点处,有 个正三角形, 个正方形.
随堂练习:
2.正三角形和正六边形可以组合密铺,在同一拼
接点处,有 个正三角形, 个正六边形或
有 个正三角形, 个正六边形.
3.边长相等的正四边形和正八边形可以进行组
合密铺吗?
4.边长相等的正三角形、正方形、和正十二边形
可以进行组合密铺吗?
活动三、创意设计 应用新知
课堂小结:
本节课你有什么收获?
随堂检测:
1.(13.呼和浩特)只用下列图形中的一种,能够进行平面
镶嵌的是 ( )
A.正十边形 B.正八边形 C.正六边形 D.正五边形
2.(08.滨州)只用下列图形不能镶嵌的是 ( )
A.三角形 B.四边形 C.正五边形 D.正六边形
3.(07.聊城)在下列四组多边形地砖中:
①正三角形与正方形;②正三角形与正六边形;③正六边形与正方形;④正八边形与正方形,将每组中的两种多边形结合,能密铺地面的是 ( )
A.① ③ ④ B.② ③ ④ C.① ② ③ D.① ② ④
4.(08.佳木斯)一幅平面图案,在某个顶点处由三个边长相等的正多边形镶嵌而成.其中的两个分别是正方形和正六边形,则第三个正多边形的边数是 ( )
A.3 B.6 C.8 D.12
谢 谢
数学活动 图形的密铺
音乐能激发或抚慰情怀,绘画使人赏心悦目,诗歌能动人心弦,哲学使人获得智慧,科学可改善物质生活,但数学能给予以上的一切。
宇宙之大 粒子之微
火箭之速 化工之巧
地球之变 生物之谜
日用之繁 数学无处不在
——华罗庚
【问题导学】
活动一、自主先学 感悟新知
请欣赏视频中展示的各种拼铺图案,感受平面图形在生活中的广泛应用.
用图案密铺
版画设计
埃舍尔的密铺图形:
http://www./luo/mei.htm
平面图形的
密铺
用形状相同或不同的平面图形进行拼接,彼此之间既无空隙、又不重叠地铺成一片,就是平面图形的密铺, 也叫做平面图形的镶嵌.
活动二、合作交流 探索新知
1.快速抢答:
(1)n边形的内角和是 °,外角和是 °;
(2)各边相等、各角相等的多边形叫做 ;
(3)正三角形的每个内角是 °, 正五边形每个内角是 °, 正n边形每个内角是 °.
2.活动探究:
问题1:五一小长假期间,小明的父母到某建材商
店选装修材料的过程中,看到以下几种形状的地
砖:正三角形、正方形、正五边形、正六边形.
如果只选择一种进行客厅地面的装修,有哪
几种可供选择
活动要求:
小组合作探究,观察实验现象、思考原理、做好记录,尝试完成活动报告1.
思考:
(1)进行密铺时,同一拼接点处,所用的正多
边形各有几个?
(2)多边形能够密铺的条件是什么?一种正多
边形能够密铺的条件是什么?
结论:用同一种可以进行密铺的正多边形有
正三角形、正四边形、正六边形.
密铺的条件:
同一拼接点处,各角之和组成一个 3600 的周角.
问题2:用形状、大小完全相同的任意三角形能
密铺成平面图案吗?任意四边形呢?其它多边形
呢?
活动要求:小组合作探究,观察实验现象、思考
原理、做好记录,尝试完成活动报告2.
思考:
(1)进行密铺时,同一拼接点处,所用的任意多
边形各有几个?
(2)进行密铺时,应注意什么?
结论:形状、大小完全相同的任意三角形、四边形能
够密铺.
① 用同一种任意三角形
等腰三角形
直角三角形
任意三角形
② 用同一种任意四边形
③用其它特殊的多边形
五边形
六边形
问题3:小明的父母打算用边长相等的正三角形、
正方形、正五边形、正六边形中的两种地砖进
行厨房地面的装修,有哪些组合方式?
1.正三角形和正方形可以组合密铺,在同一拼接
点处,有 个正三角形, 个正方形.
随堂练习:
2.正三角形和正六边形可以组合密铺,在同一拼
接点处,有 个正三角形, 个正六边形或
有 个正三角形, 个正六边形.
3.边长相等的正四边形和正八边形可以进行组
合密铺吗?
4.边长相等的正三角形、正方形、和正十二边形
可以进行组合密铺吗?
活动三、创意设计 应用新知
课堂小结:
本节课你有什么收获?
随堂检测:
1.(13.呼和浩特)只用下列图形中的一种,能够进行平面
镶嵌的是 ( )
A.正十边形 B.正八边形 C.正六边形 D.正五边形
2.(08.滨州)只用下列图形不能镶嵌的是 ( )
A.三角形 B.四边形 C.正五边形 D.正六边形
3.(07.聊城)在下列四组多边形地砖中:
①正三角形与正方形;②正三角形与正六边形;③正六边形与正方形;④正八边形与正方形,将每组中的两种多边形结合,能密铺地面的是 ( )
A.① ③ ④ B.② ③ ④ C.① ② ③ D.① ② ④
4.(08.佳木斯)一幅平面图案,在某个顶点处由三个边长相等的正多边形镶嵌而成.其中的两个分别是正方形和正六边形,则第三个正多边形的边数是 ( )
A.3 B.6 C.8 D.12
谢 谢
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
