22.3 实际问题与二次函数 课后练习(1)2021-2022学年人教版九年级数学上册(Word版含答案)
文档属性
| 名称 | 22.3 实际问题与二次函数 课后练习(1)2021-2022学年人教版九年级数学上册(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 291.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-28 11:33:14 | ||
图片预览


文档简介
2021——2022学年度人教版九年级数学上册 第二十二章 二次函数
22.3 实际问题与二次函数 课后练习1
一、选择题
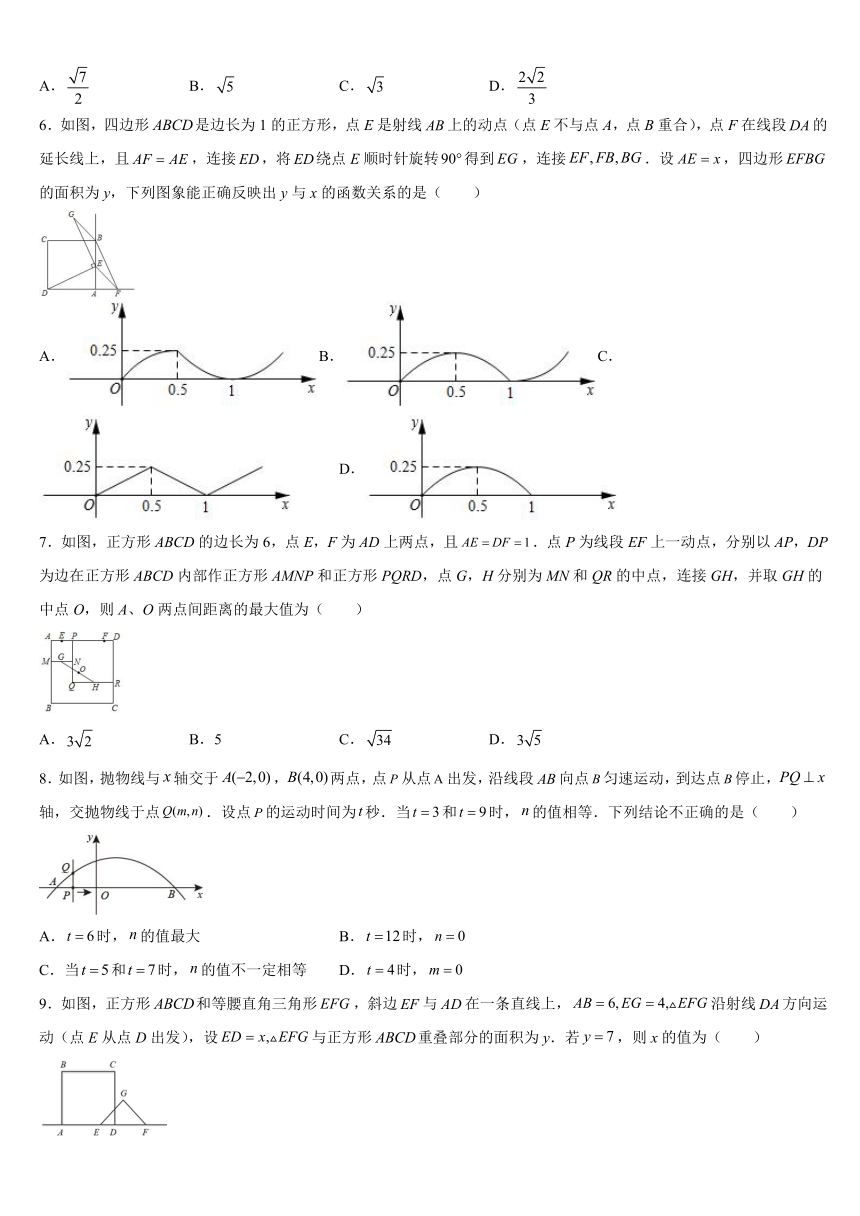
1.用总长为a米的材料做成如图1的矩形窗框,设窗框的宽为x米,窗框的面积为y米2,y关于x的函数图象如图2,则a的值是( )
A.9 B.8 C.6 D.不能确定
2.如图,预防新冠肺炎疫情期间,某校在校门口用塑料膜围成一个临时隔离区,隔离区一面靠长为的墙,隔离区分成两个区域,中间用塑料膜隔开.已知整个隔离区塑料膜总长为,如果隔离区出入口的大小不计,并且隔离区靠墙的一面不能超过墙长.小明认为:隔离区的最大面积为;小亮认为:隔离区的面积可能为,则( )
A.小明正确,小亮错误 B.小明错误,小亮正确 C.两人均正确 D.两人均错误
3.如图,小明以抛物线y=x2-2x+4为灵感设计了一款杯子,若AB=4,DE=2,则杯子的高CE为( )
A.4 B.5 C.6 D.7
4.用一段长为的篱笆围成一个矩形菜园,设菜园的对角线长为,面积为,则y与x的函数图像大致是( )
A.B.C. D.
5.如果一个矩形的周长与面积的差是定值,我们称这个矩形为“定差值矩形”.如图,在矩形中, ,,,那么这个“定差值矩形”的对角线 的长的最小值为( )
A. B. C. D.
6.如图,四边形是边长为1的正方形,点E是射线上的动点(点E不与点A,点B重合),点F在线段的延长线上,且,连接,将绕点E顺时针旋转得到,连接.设,四边形的面积为y,下列图象能正确反映出y与x的函数关系的是( )
A.B.C. D.
7.如图,正方形ABCD的边长为6,点E,F为AD上两点,且.点P为线段EF上一动点,分别以AP,DP为边在正方形ABCD内部作正方形AMNP和正方形PQRD,点G,H分别为MN和QR的中点,连接GH,并取GH的中点O,则A、O两点间距离的最大值为( )
A. B.5 C. D.
8.如图,抛物线与轴交于,两点,点从点出发,沿线段向点匀速运动,到达点停止,轴,交抛物线于点.设点的运动时间为秒.当和时,的值相等.下列结论不正确的是( )
A.时,的值最大 B.时,
C.当和时,的值不一定相等 D.时,
9.如图,正方形和等腰直角三角形,斜边与在一条直线上,沿射线方向运动(点E从点D出发),设与正方形重叠部分的面积为y.若,则x的值为( )
A.或 B.或 C.或 D.或
10.如图,平面直角坐标系中,抛物线与x轴交于A,B两点,与y轴交于点C.直线与抛物线交于点D,与直线交于点E.连接,.若,则a的值是( )
A.1 B.2 C.3 D.4
二、填空题
11.如图1,正方形中,点为的中点,连接,动点从点出发,沿运动,同时,动点从点出发,沿向点运动,,两点同时到达点,设点的运动时间为,的面积为,则关于的函数图象如图2,当与全等时,的长为________cm.
12.如图,在Rt△ACB中,∠ACB=90°,AC=BC,D是AB上的一个动点,连接CD,将△BCD绕点C顺时针旋转90°得到△ACE,连接DE,则△ADE面积的最大值等于____________.
13.如图,在平面直角坐标系中,抛物线的顶点为M,直线与x轴平行,且与抛物线交于点A和点B,如果为等腰直角三角形,我们把抛物线上A、B两点之间部分与线段围成的图形称为该抛物线的准蝶形,顶点M称为碟顶,线段的长称为碟宽.抛物线的碟宽为__________.
14.如图,点是y轴正半轴上的点,点A的坐标为,以AC为边作等腰直角三角形ABC,其中,,,以点B为顶点的抛物线经过点A且和x轴交于另一点D,交y轴于点E.
(1)点B的坐标为_____________;
(2)求抛物线的函数表达式;
(3)在第一象限的抛物线上是否存在点P,使得?若存在求点P的坐标,不存在则说明理由.
15.如图,在平面直角坐标系xOy中,抛物线y=﹣x2+6x+c的对称轴与x轴交于点A,在直线AB:y=kx+3上取一点B,使点B在第四象限,且到两坐标轴的距离和为7,设P是抛物线的对称轴上的一点,点Q在抛物线上,若以点A,B,P,Q为顶点的四边形为正方形,则c的值为________.
三、解答题
16.如图,抛物线y=ax2+bx+c(a≠0)与直线y=x+1相交于A(﹣1,0),B(4,m)两点,且抛物线经过点C(5,0).
(1)求抛物线的解析式.
(2)点P是抛物线上的顶点,求△ABP的面积.
17.某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边周长为米的篱笆围成.已知墙长为米(如图所示),设这个苗圃园垂直于墙的一边长为米.
(1)若苗圃园的面积为平方米,求;
(2)若平行于墙的一边长不小于米,求这个苗圃园的面积的最大值和最小值.
18.已知抛物线C的解析式为,与y轴交于点A.
(1)直接写出抛物线C的开口方向及顶点坐标(用含m的式子表示);
(2)过点A作轴交抛物线C于另一点B,当时,求此抛物线C的解析式;
(3)在抛物线C的对称轴上存在一点P,使得为等腰直角三角形,请直接写出此时m的值.
19.如图,抛物线与轴交于、两点,与轴交于点.直线与抛物线交于、两点,与轴交于点,点的坐标为.
(1)求抛物线的解析式与直线的解析式;
(2)若点是抛物线上的点且在直线上方,连接、,求当面积最大时点的坐标及该面积的最大值;
(3)若点是轴上的点,且,求点的坐标.
20.如图,在矩形中,, ,点从点开始沿边向点以2cm/s的速度移动,点从点开始沿边向点以3cm/s的速度移动,如果、分别从、同时出发,当一点到达终点时,另一个点随即停止移动.
(1)经过几秒,的面积等于18?
(2)在运动过程中,经过几秒时,的面积最大?最大面积是多少?
21.如图所示,在中,,厘米,.点从点开始沿边向点以厘米/秒的速度移动,点从点开始沿边向点以厘米/秒的速度移动,当点运动到点时停止,点也同时停止.
(1)如果点,分别从点,同时出发,那么几秒后,的面积等于平方厘米?
(2)如果点,分别从点,同时出发,问第几秒时,四边形的面积最小?其最小面积为多少?
22.在平面直角坐标系中,已知抛物线经过A(-4,0),B(0,-4),C(2,0)三点.
(1)求抛物线的解析式;
(2)若点P为抛物线对称轴上一个动点,求△PBC周长最小时的P点坐标;
(3)若点M为第三象限内抛物线上一动点,点M的横坐标为m,△AMB的面积为S.求S关于m的函数关系式,并求出S的最大值和M点的坐标.
23.如图,在平面直角坐标系中,已知点A坐标为(2,4),AB⊥x轴,垂足为点B,连接OA,抛物线y=x2从点O沿OA方向平移,与直线AB交于点P,抛物线的顶点M到A点时停止移动.
(1)求线段OA所在直线的函数解析式是 ;
(2)设抛物线顶点M的横坐标为m,
①用含m的代数式表示点P的坐标;
②当m为何值时,线段PA最长?并求出此时PA的长;
(3)若平移后的抛物线交y轴于点Q,是否存在点Q,使得△OMQ为等腰三角形?若存在,请直接写出满足条件的Q点的坐标;若不存在,请说明理由.
【参考答案】
1.C 2.B 3.C 4.B 5.C 6.B 7.B 8.C 9.B 10.B
11.
12.
13.6
14.(1);(2);(3)存在,点P的坐标为或.设,根据列出方程,即可求解.
15.﹣5或﹣7
16.(1);(2)15
17.(1)x=12;(2)88平方米、平方米.
18.(1)开口向上,;(2)或;(3)或
19.(1)抛物线的解析式为,直线的解析式为;(2)的面积的最大值为,.(3)的坐标为或.
20.(1)2s或3s;(2)2.5秒,
21.(1)1秒;(2)秒,
22.(1)抛物线的解析式为y=x2+x-4.(2)点P的坐标为(-1,-3);(3)S=-m2-4m(-4<m<0),S的最大值为4.此时,点M的坐标为(-2,-4)
23.(1)y=2x;(2)①P(2,m2﹣2m+4);②线段PA有最大值且当m=1时,PA的最大值为1;(3)存在,Q(0,5﹣2)或(0,8)
22.3 实际问题与二次函数 课后练习1
一、选择题
1.用总长为a米的材料做成如图1的矩形窗框,设窗框的宽为x米,窗框的面积为y米2,y关于x的函数图象如图2,则a的值是( )
A.9 B.8 C.6 D.不能确定
2.如图,预防新冠肺炎疫情期间,某校在校门口用塑料膜围成一个临时隔离区,隔离区一面靠长为的墙,隔离区分成两个区域,中间用塑料膜隔开.已知整个隔离区塑料膜总长为,如果隔离区出入口的大小不计,并且隔离区靠墙的一面不能超过墙长.小明认为:隔离区的最大面积为;小亮认为:隔离区的面积可能为,则( )
A.小明正确,小亮错误 B.小明错误,小亮正确 C.两人均正确 D.两人均错误
3.如图,小明以抛物线y=x2-2x+4为灵感设计了一款杯子,若AB=4,DE=2,则杯子的高CE为( )
A.4 B.5 C.6 D.7
4.用一段长为的篱笆围成一个矩形菜园,设菜园的对角线长为,面积为,则y与x的函数图像大致是( )
A.B.C. D.
5.如果一个矩形的周长与面积的差是定值,我们称这个矩形为“定差值矩形”.如图,在矩形中, ,,,那么这个“定差值矩形”的对角线 的长的最小值为( )
A. B. C. D.
6.如图,四边形是边长为1的正方形,点E是射线上的动点(点E不与点A,点B重合),点F在线段的延长线上,且,连接,将绕点E顺时针旋转得到,连接.设,四边形的面积为y,下列图象能正确反映出y与x的函数关系的是( )
A.B.C. D.
7.如图,正方形ABCD的边长为6,点E,F为AD上两点,且.点P为线段EF上一动点,分别以AP,DP为边在正方形ABCD内部作正方形AMNP和正方形PQRD,点G,H分别为MN和QR的中点,连接GH,并取GH的中点O,则A、O两点间距离的最大值为( )
A. B.5 C. D.
8.如图,抛物线与轴交于,两点,点从点出发,沿线段向点匀速运动,到达点停止,轴,交抛物线于点.设点的运动时间为秒.当和时,的值相等.下列结论不正确的是( )
A.时,的值最大 B.时,
C.当和时,的值不一定相等 D.时,
9.如图,正方形和等腰直角三角形,斜边与在一条直线上,沿射线方向运动(点E从点D出发),设与正方形重叠部分的面积为y.若,则x的值为( )
A.或 B.或 C.或 D.或
10.如图,平面直角坐标系中,抛物线与x轴交于A,B两点,与y轴交于点C.直线与抛物线交于点D,与直线交于点E.连接,.若,则a的值是( )
A.1 B.2 C.3 D.4
二、填空题
11.如图1,正方形中,点为的中点,连接,动点从点出发,沿运动,同时,动点从点出发,沿向点运动,,两点同时到达点,设点的运动时间为,的面积为,则关于的函数图象如图2,当与全等时,的长为________cm.
12.如图,在Rt△ACB中,∠ACB=90°,AC=BC,D是AB上的一个动点,连接CD,将△BCD绕点C顺时针旋转90°得到△ACE,连接DE,则△ADE面积的最大值等于____________.
13.如图,在平面直角坐标系中,抛物线的顶点为M,直线与x轴平行,且与抛物线交于点A和点B,如果为等腰直角三角形,我们把抛物线上A、B两点之间部分与线段围成的图形称为该抛物线的准蝶形,顶点M称为碟顶,线段的长称为碟宽.抛物线的碟宽为__________.
14.如图,点是y轴正半轴上的点,点A的坐标为,以AC为边作等腰直角三角形ABC,其中,,,以点B为顶点的抛物线经过点A且和x轴交于另一点D,交y轴于点E.
(1)点B的坐标为_____________;
(2)求抛物线的函数表达式;
(3)在第一象限的抛物线上是否存在点P,使得?若存在求点P的坐标,不存在则说明理由.
15.如图,在平面直角坐标系xOy中,抛物线y=﹣x2+6x+c的对称轴与x轴交于点A,在直线AB:y=kx+3上取一点B,使点B在第四象限,且到两坐标轴的距离和为7,设P是抛物线的对称轴上的一点,点Q在抛物线上,若以点A,B,P,Q为顶点的四边形为正方形,则c的值为________.
三、解答题
16.如图,抛物线y=ax2+bx+c(a≠0)与直线y=x+1相交于A(﹣1,0),B(4,m)两点,且抛物线经过点C(5,0).
(1)求抛物线的解析式.
(2)点P是抛物线上的顶点,求△ABP的面积.
17.某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边周长为米的篱笆围成.已知墙长为米(如图所示),设这个苗圃园垂直于墙的一边长为米.
(1)若苗圃园的面积为平方米,求;
(2)若平行于墙的一边长不小于米,求这个苗圃园的面积的最大值和最小值.
18.已知抛物线C的解析式为,与y轴交于点A.
(1)直接写出抛物线C的开口方向及顶点坐标(用含m的式子表示);
(2)过点A作轴交抛物线C于另一点B,当时,求此抛物线C的解析式;
(3)在抛物线C的对称轴上存在一点P,使得为等腰直角三角形,请直接写出此时m的值.
19.如图,抛物线与轴交于、两点,与轴交于点.直线与抛物线交于、两点,与轴交于点,点的坐标为.
(1)求抛物线的解析式与直线的解析式;
(2)若点是抛物线上的点且在直线上方,连接、,求当面积最大时点的坐标及该面积的最大值;
(3)若点是轴上的点,且,求点的坐标.
20.如图,在矩形中,, ,点从点开始沿边向点以2cm/s的速度移动,点从点开始沿边向点以3cm/s的速度移动,如果、分别从、同时出发,当一点到达终点时,另一个点随即停止移动.
(1)经过几秒,的面积等于18?
(2)在运动过程中,经过几秒时,的面积最大?最大面积是多少?
21.如图所示,在中,,厘米,.点从点开始沿边向点以厘米/秒的速度移动,点从点开始沿边向点以厘米/秒的速度移动,当点运动到点时停止,点也同时停止.
(1)如果点,分别从点,同时出发,那么几秒后,的面积等于平方厘米?
(2)如果点,分别从点,同时出发,问第几秒时,四边形的面积最小?其最小面积为多少?
22.在平面直角坐标系中,已知抛物线经过A(-4,0),B(0,-4),C(2,0)三点.
(1)求抛物线的解析式;
(2)若点P为抛物线对称轴上一个动点,求△PBC周长最小时的P点坐标;
(3)若点M为第三象限内抛物线上一动点,点M的横坐标为m,△AMB的面积为S.求S关于m的函数关系式,并求出S的最大值和M点的坐标.
23.如图,在平面直角坐标系中,已知点A坐标为(2,4),AB⊥x轴,垂足为点B,连接OA,抛物线y=x2从点O沿OA方向平移,与直线AB交于点P,抛物线的顶点M到A点时停止移动.
(1)求线段OA所在直线的函数解析式是 ;
(2)设抛物线顶点M的横坐标为m,
①用含m的代数式表示点P的坐标;
②当m为何值时,线段PA最长?并求出此时PA的长;
(3)若平移后的抛物线交y轴于点Q,是否存在点Q,使得△OMQ为等腰三角形?若存在,请直接写出满足条件的Q点的坐标;若不存在,请说明理由.
【参考答案】
1.C 2.B 3.C 4.B 5.C 6.B 7.B 8.C 9.B 10.B
11.
12.
13.6
14.(1);(2);(3)存在,点P的坐标为或.设,根据列出方程,即可求解.
15.﹣5或﹣7
16.(1);(2)15
17.(1)x=12;(2)88平方米、平方米.
18.(1)开口向上,;(2)或;(3)或
19.(1)抛物线的解析式为,直线的解析式为;(2)的面积的最大值为,.(3)的坐标为或.
20.(1)2s或3s;(2)2.5秒,
21.(1)1秒;(2)秒,
22.(1)抛物线的解析式为y=x2+x-4.(2)点P的坐标为(-1,-3);(3)S=-m2-4m(-4<m<0),S的最大值为4.此时,点M的坐标为(-2,-4)
23.(1)y=2x;(2)①P(2,m2﹣2m+4);②线段PA有最大值且当m=1时,PA的最大值为1;(3)存在,Q(0,5﹣2)或(0,8)
同课章节目录
