4.2.2指数函数的图象和性质(知识梳理+例题+变式+练习)(解析版)
文档属性
| 名称 | 4.2.2指数函数的图象和性质(知识梳理+例题+变式+练习)(解析版) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-28 18:05:44 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
4.2.2指数函数的图象和性质
知识点 指数函数的图象和性质
a>1 0图象
性 质 定义域 R
值域
过定点 过定点 ,即x=0时,y=1
函数值 的变化 当x<0时, 当x>0时,y>1 当x>0时,01
单调性 在R上是增函数 在R上是减函数
对称性 y=ax与y=x的图象关于y轴对称
【思考】
指数函数y=ax(a>0且a≠1)的底数a对图象有哪些影响?
【提示】(1)底数a与1的大小关系决定了指数函数图象的增减性:a>1时,图象单调递增;0<a<1时,图象单调递减.
(2)底数的大小决定了图象相对位置的高低:不论是a>1,还是0<a<1,在第一象限内底数越小,函数图象越靠近x轴;底数越大,函数图象越靠近y轴.
【基础自测】
1.判断正误(正确的画“√”,错误的画“×”)
(1)函数y=x-1的值域是(0,+∞). ( )
(2)已知函数f(x)=x,若实数m,n满足f(m)>f(n),则m>n. ( )
(3)指数函数f(x)的图象过点. ( )
(4)函数y=2的定义域是R. ( )
【答案】(1)×(2)√(3)√(4)×
2.函数y= 的定义域是 ( )
A.[0,+∞) B.(-∞,0]
C.[1,+∞) D.(-∞,+∞)
【答案】B
【解析】∵1-3x≥0,即3x≤1,∴x≤0,即x∈(-∞,0].故选B.
3.函数y=1-2x,x∈[0,1]的值域是 ( )
A.[0,1] B.[-1,0]
C. D.
【答案】B
【解析】由指数函数y=2x在x∈[0,1]上单调递增知1≤2x≤2,∴y=1-2x∈[-1,0].
4.(多选)下列函数中,是增函数的为 ( )
A.y=x B.y=(+1)x
C.y=2-x D.y=(a2+2)x
【答案】BD
题型一 指数函数的定义域和值域
【学透用活】
【例1】求下列函数的定义域和值域:
(1)y=2;(2)y=-|x|;(3)y= .
【解析】(1)x应满足x-4≠0,∴x≠4,
∴定义域为{x|x≠4,x∈R}.
∵≠0,∴2≠1,
∴y=2的值域为{y|y>0,且y≠1}.
(2)定义域为R.
∵|x|≥0,∴y=-|x|=|x|≥0=1,∴此函数的值域为[1,+∞).
(3)由题意知1-x≥0,∴x≤1=0,∴x≥0,
∴定义域为{x|x≥0,x∈R}.
∵x≥0,∴x≤1.
又∵x>0,∴0<x≤1.∴0≤1-x<1,
∴0≤y<1,∴此函数的值域为[0,1).
【方法技巧】
求指数型函数的定义域和值域的一般方法
(1)求与指数函数有关的函数的定义域时,首先观察函数是y=ax型还是y=af(x)型,前者的定义域是R,后者的定义域与f(x)的定义域一致,而求y=型函数的定义域时,往往转化为解指数不等式(组).
(2)求与指数函数有关的函数的值域时,一方面要考虑函数的定义域和单调性,另一方面要注意指数函数的值域是(0,+∞).一般地,对于y=af(x)型函数,应先求出f(x)的值域A,再画出y=ax(x∈A)的图形或利用函数的单调性,就能很容易求出原函数的值域.
【提醒】(1)通过建立不等关系求定义域时,要注意解集为各不等关系解集的交集.
(2)当指数型函数的底数含字母时,在求定义域、值域时要注意分类讨论.
【变式训练】
求下列函数的定义域、值域:
(1)y=;(2)y=2;(3)y=4x-2x+1.
【解析】(1)函数的定义域为R.∵y===1-,
又∵3x>0,∴1+3x>1,∴0<<1,∴-1<-<0,
∴0<1-<1,∴函数的值域为(0,1).
(2)函数的定义域为R.∵2x-x2=-(x-1)2+1≤1,
∴2≤2,即y≤2.又2>0,∴函数的值域为(0,2].
(3)函数的定义域为R. y=(2x)2-2x+1=2+,
∵2x>0,∴当2x=,即x=-1时,y取最小值,
∴函数的值域为.
题型二 指数函数的图象及应用
【学透用活】
1.指数函数图象的特征
同一坐标系中,画出不同底数的指数函数的图象如图所示.
直线x=1与四个指数函数y=ax,y=bx,y=cx,y=dx的交点依次为(1,a),(1,b),(1,c),(1,d),所以有0<b<a<1<d<c,因此可得出以下结论:在y轴的右侧,底数越大,图象越高,简称“底大图高”.
2.指数函数图象的变换
(1)平移规律:设b>0,
①y=ax的图象y=ax+b的图象;
②y=ax的图象y=ax-b的图象;
③y=ax的图象y=ax+b的图象;
④y=ax的图象y=ax-b的图象.
(2)对称规律
y=ax(a>0, 且a≠1)的图象 与y=a-x的图象关于y轴对称
与y=-ax的图象关于x轴对称
与y=-a-x的图象关于坐标原点对称
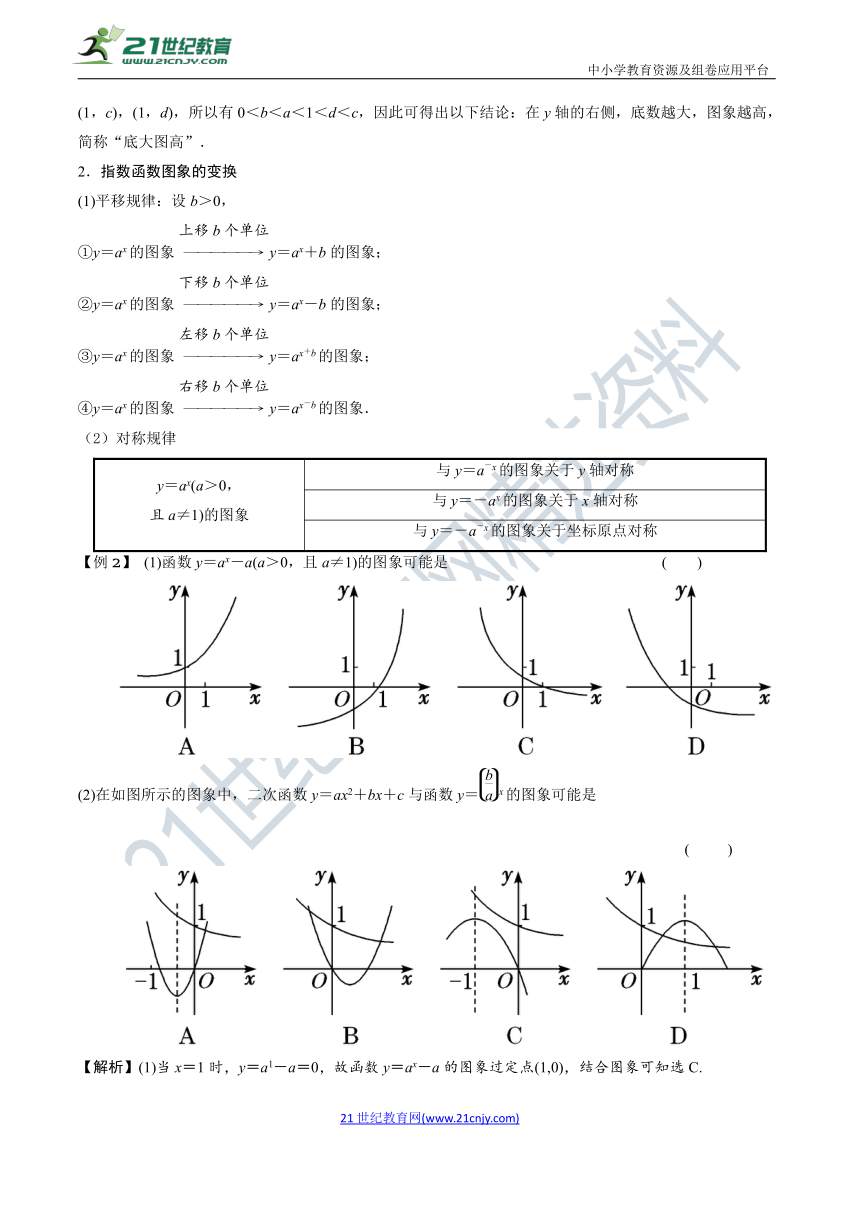
【例2】 (1)函数y=ax-a(a>0,且a≠1)的图象可能是 ( )
(2)在如图所示的图象中,二次函数y=ax2+bx+c与函数y=x的图象可能是 ( )
【解析】(1)当x=1时,y=a1-a=0,故函数y=ax-a的图象过定点(1,0),结合图象可知选C.
(2)根据图中二次函数图象可知c=0,∴二次函数y=ax2+bx,∵>0,
∴二次函数的对称轴为x=-<0,排除B、D.
对于A、C,都有0<<1,∴-<-<0,C不符合,故选A.
【方法技巧】
指数函数图象问题的处理技巧
(1)抓住图象上的特殊点,如指数函数的图象过定点.
(2)利用图象变换,如函数图象的平移变换(左右平移、上下平移).
(3)利用函数的奇偶性与单调性.奇偶性确定函数的对称情况,单调性决定函数图象的走势.
【变式训练】
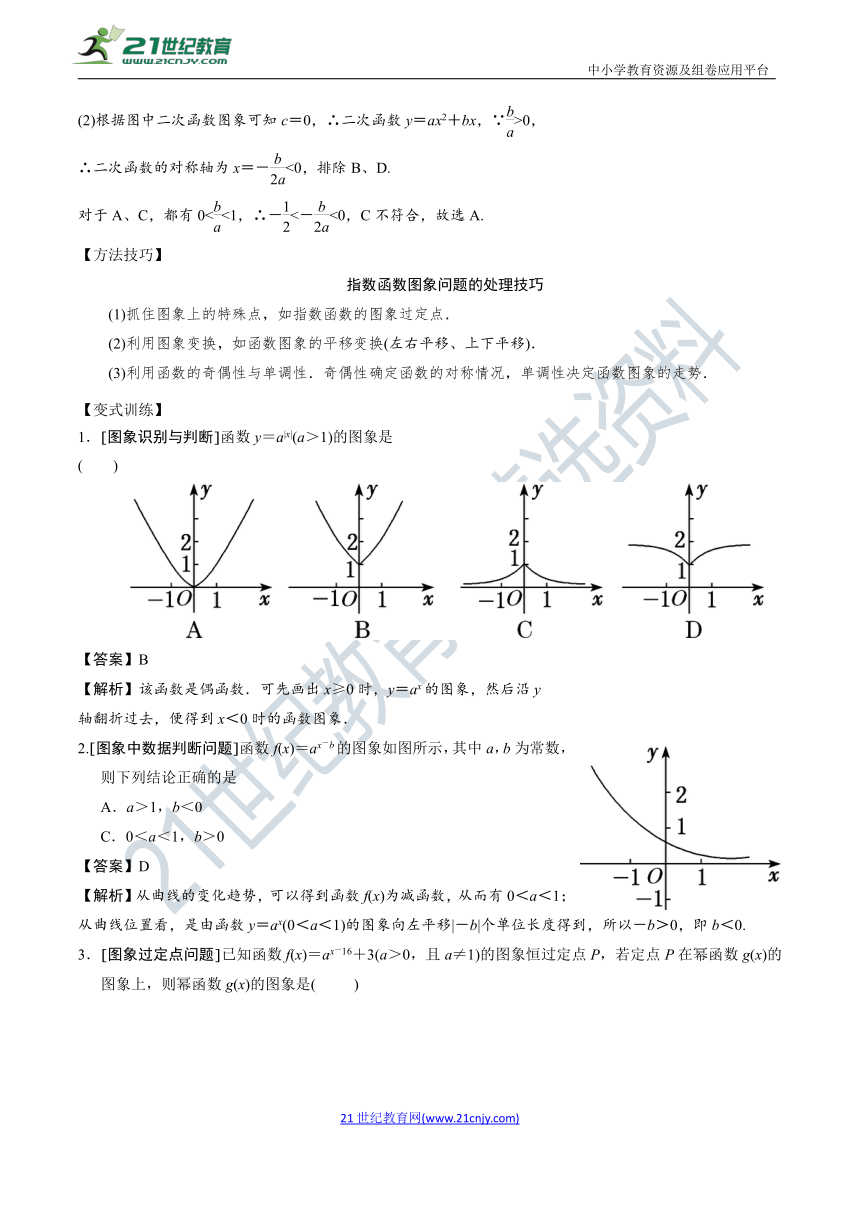
1.[图象识别与判断]函数y=a|x|(a>1)的图象是 ( )
【答案】B
【解析】该函数是偶函数.可先画出x≥0时,y=ax的图象,然后沿y
轴翻折过去,便得到x<0时的函数图象.
2.[图象中数据判断问题]函数f(x)=ax-b的图象如图所示,其中a,b为常数,则下列结论正确的是 ( )
A.a>1,b<0 B.a>1,b>0
C.0<a<1,b>0 D.0<a<1,b<0
【答案】D
【解析】从曲线的变化趋势,可以得到函数f(x)为减函数,从而有0<a<1;
从曲线位置看,是由函数y=ax(0<a<1)的图象向左平移|-b|个单位长度得到,所以-b>0,即b<0.
3.[图象过定点问题]已知函数f(x)=ax-16+3(a>0,且a≠1)的图象恒过定点P,若定点P在幂函数g(x)的图象上,则幂函数g(x)的图象是( )
【答案】A
【解析】 f(x)=ax-16+3恒过定点P(16,4),
设幂函数g(x)=xα,则16α=4,∴α=,∴g(x)=.
3.[图象过定点问题]已知函数f(x)=ax-16+3(a>0,且a≠1)的图象恒过
定点P,若定点P在幂函数g(x)的图象上,则幂函数g(x)的图象是
( )
【答案】A
【解析】 f(x)=ax-16+3恒过定点P(16,4),设幂函数g(x)=xα,则16α=4,∴α=,∴g(x)=.
4.[图象的应用]已知直线y=2a与函数y=|2x-2|的图象有两个公共点,
求实数a的取值范围.
【解析】函数y=|2x-2|的图象如图所示.要使直线y=2a与
该图象有两个公共点,则有0<2a<2,即0<a<1,故实
数a的取值范围为(0,1).
题型三 比较大小问题
【探究发现】
(1)函数幂的形式有哪些?
(2)它们的单调性如何判断?
【提示】(1)幂的形式的函数有幂函数和指数函数.
(2)幂函数y=xα,x>0,α>0时为增函数,指数函数y=ax,当a>1时为增函数,当0<a<1时为减函数.
【学透用活】
【例3】比较下列各题中两个值的大小:
(1)1.70.3,0.93.1;(2)-1.8,-2.5;
(3)0.20.3,0.30.2.
【解析】(1)因为1.70.3>1.70=1,0.93.1<0.90=1,
所以1.70.3>0.93.1.
(2)因为0<<1,所以函数y=x在其定义域R上单调递减,又-1.8>-2.5,所以-1.8<-2.5.
(3)因为0<0.2<0.3<1,所以指数函数y=0.2x与y=0.3x在定义域R上均是减函数,且在区间(0,+∞)上函数y=0.2x的图象在函数y=0.3x的图象的下方,所以0.20.2<0.30.2.
又根据指数函数y=0.2x在R上是减函数,可得0.20.3<0.20.2,所以0.20.3<0.30.2.
【方法技巧】
【变式训练】
1.已知a=,b=,c=,则a,b,c的大小关系是 ( )
A.c<a<b B.a<b<c
C.b<a<c D.c<b<a
【答案】D
【解析】 (1)原式=(-1)·+-+1
=+500-10(+2)+1
=+10-10-20+1=-.
(2)原式=(63)+32-(73)-(5-3)=36+9-7-5=33.
(3)3π×π++1=π+22×+1=1π+24+1=18.
2.比较下列各组数的大小:
(1)1.52.5和1.53.2;
(2)0.6-1.2和0.6-1.5;
(3)1.50.3和0.81.2.
【解析】(1)∵函数y=1.5x在R上是增函数,2.5<3.2,∴1.52.5<1.53.2.
(2)∵函数y=0.6x在R上是减函数,-1.2>-1.5,∴0.6-1.2<0.6-1.5.
(3)由指数函数的性质知1.50.3>1.50=1,
而0.81.2<0.80=1,∴1.50.3>0.81.2.
【课堂思维激活】
一、综合性——强调融会贯通
1.已知函数f(x)=ax(a>0,且a≠1).
(1)若f(1)+f(-1)=,求f(2)+f(-2)的值;
(2)若函数f(x)在[-1,1]上的最大值与最小值的差为,求实数a的值.
请根据题设条件把下面的解析补充完整.
【解析】(1)∵f(x)=ax,f(1)+f(-1)=,
∴a+=,解得a=2或,
当a=2时,f(x)=,f(2)+f(-2)=,
当a=时,f(x)=,f(2)+f(-2)=,
故f(2)+f(-2)=.
(2)当a>1时,f(x)=ax在[-1,1]上单调递增,
∴f(x)max-f(x)min=f(1)-f(-1)=a-a-1=,
化简得3a2-8a-3=0,解得a=-(舍去)或a=3.
当0<a<1时,f(x)=ax在[-1,1]上单调递减,
∴f(x)max-f(x)min=f(-1)-f(1)=a-1-a=,化简得3a2+8a-3=0.
解得a=-3(舍去)或a=.
综上,实数a的值为3或.
二、应用性——强调学以致用
2.[好题共享——选自苏教版新教材]有些家用电器(如冰箱等)使用了氟化
物,氟化物的释放破坏了大气上层的臭氧层,使臭氧含量Q呈指数函数型
变化,在氟化物排放量维持某种水平时,具有关系式Q=Q0e-0.002 5t,其中
Q0是臭氧的初始量.
(1)随时间t的增加,臭氧的含量是增加还是减少?
(2)试估计多少年以后将会有一半的臭氧消失.(用计算器计算)
【析题建模】
―→
【解析】(1)Q=Q0e-0.002 5t,∵u=-0.002 5t随t的增大而减少,且e>1,
∴e-0.002 5t的值也随t的增大而减小.
∴随时间t的增加,臭氧的含量减少.
(2)由题意得Q0=Q0e-0.002 5t,即e-0.002 5t=.
借助计算器计算得t≈277.2年,
∴278年后将会有一半的臭氧消失.
三、创新性——强调创新意识和创新思维
3.已知四个函数f(x)=2x,g(x)=x,h(x)=3x,p(x)=x,若y=f(x),y=
g(x)的图象如图所示.
(1)请在如图坐标系中画出y=h(x),y=p(x)的图象,并根据这四个函数的图象
抽象出指数函数具有哪些性质?
(2)举出在实际情境能够抽象出指数函数的一个实例并说明理由.
【解析】(1)画出y=h(x),y=p(x)的图象如图所示:4个
函数都是y=ax(a>0,a≠1)的形式,它们的性质有:
①定义域为R;
②值域为(0,+∞);
③都过定点(0,1);
④当a>1时,函数在定义域内单调递增,0<a<1时,
函数在定义域内单调递减;
⑤a>1时,若x<0,则0<y<1,若x>0,则y>1.
0<a<1时,若x>0,则0<y<1,若x<0,则y>1;
⑥对于函数y=ax(a>0,且a≠1),y=bx(b>0,且b≠1),
当a>b>1时,
若x<0,则0<ax<bx<1;若x=0,则ax=bx=1;
若x>0,则ax>bx>1.
当0<a<b<1时,
若x<0,则ax>bx>1;若x=0,则ax=bx=1;若x>0,则0<ax<bx<1.
(2)举例:原来有一个细胞,细胞分裂的规则是细胞由一个分裂成2个,则经过x次分裂,细胞个数y,
则y=2x,是一个指数函数.
1.函数f(x)=是( )
A.偶函数,在(0,+∞)是增函数
B.奇函数,在(0,+∞)是增函数
C.偶函数,在(0,+∞)是减函数
D.奇函数,在(0,+∞)是减函数
【答案】B
【解析】因为f(-x)=-f(x),所以f(x)为奇函数,
又因为y=2x是增函数,y=2-x为减函数,
故f(x)=为增函数.故选B.
2.(多选)设函数f(x)=a-|x|(a>0,且a≠1),若f(2)=4,则( )
A.f(-2)>f(-1) B.f(-1)>f(-2)
C.f(-2)>f(2) D.f(-4)>f(3)
【答案】AD
【解析】由f(2)=a-2=4得a=,即f(x)=-|x|=2|x|,故f(-2)>f(-1),f(-2)=f(2),f(-4)=f(4)>f(3),所以A、D正确.
3.函数y=ax在[0,1]上的最大值与最小值的和为3,则函数y=2ax-1在[0,1]上的最大值是( )
A.6 B.1
C.3 D.
【答案】C
【解析】函数y=ax在[0,1]上是单调的,最大值与最小值都在端点处取到,故有a0+a1=3,解得a=2,因此函数y=2ax-1=4x-1在[0,1]上是单调递增函数,当x=1时,ymax=3.
4.若函数f(x)=a|2x-4|(a>0,且a≠1)满足f(1)=,则f(x)的单调递减区间是( )
A.(-∞,2] B.[2,+∞)
C.[-2,+∞) D.(-∞,-2]
【答案】B
【解析】由f(1)=,得a2=,于是a=,因此f(x)=|2x-4|.
令t=|2x-4|,∴h(t)=t为减函数.
因为g(x)=|2x-4|在[2,+∞)上单调递增,所以f(x)的单调递减区间是[2,+∞).故选B.
5.若关于x的不等式a2x≥a3-x(0A.1 B.3
C.6 D.9
【答案】D
【解析】∵06.若函数f(x)=则不等式f(x)≥的解集为________.
【答案】{x|0≤x≤1}
【解析】f(x)≥ 或∴0≤x≤1,
故不等式f(x)≥的解集是{x|0≤x≤1}.
7.春天来了,某池塘中的荷花枝繁叶茂,已知每一天新长出荷叶覆盖水面面积是前一天的2倍,若荷叶20天可以完全长满池塘水面,当荷叶刚好覆盖水面面积一半时,荷叶已生长了________天.
【答案】19
【解析】假设第一天荷叶覆盖水面面积为1,则荷叶覆盖水面面积y与生长时间的函数关系为y=2x-1,因为荷叶20天可以完全长满池塘水面,故当荷叶刚好覆盖水面面积一半时,×220-1=2x-1,解得x=19,所以生长19天时,荷叶布满水面一半.
8.函数f(x)=(a>0,且a≠1)是R上的减函数,则a的取值范围是________.
【答案】
【解析】由单调性定义,f(x)为减函数应满足:即≤a<1.
9.已知指数函数f(x)的图象过点.
(1)求函数f(x)的解析式;
(2)已知f(|x|)>f(1),求x的取值范围.
【解析】(1)设f(x)=ax(a>0,且a≠1).将点代入得=a2.
解得a=.故f(x)=x.
(2)由(1)知f(x)=x,显然f(x)在R上是减函数,又f(|x|)>f(1),所以|x|<1,解得-1即x的取值范围为(-1,1).
10.对于函数f(x)=a-(x∈R).
(1)判断并证明函数的单调性;
(2)是否存在实数a,使函数f(x)为奇函数?证明你的结论.
【解析】(1)函数f(x)为R上的增函数.证明如下:函数f(x)的定义域为R.任取x1,x2∈R,且x1因为y=2x是R上的增函数,x1所以2x1-2x2<0,又2x1+1>0,2x2+1>0,所以f(x1)-f(x2)<0,即f(x1)(2)∵x∈R,f(x)是奇函数,∴f(0)=0,即a=1.所以存在实数a=1,使函数f(x)为奇函数.
证明如下:当a=1时,f(x)=1-=.
对任意x∈R,f(-x)===-=-f(x),又f(x)的定义域为R,故f(x)为奇函数.
11.如图,面积为8的平行四边形OABC的对角线AC⊥CO,AC与BO交于点E.若指数函数y=ax(a>0,且a≠1)的图象经过E,B两点,则a等于( )
A. B.
C.2 D.3
【答案】A
【解析】设点C(0,m)(m>0),则由已知可依次得A,E,B.又因为点E,B在指数函数y=ax的图象上,所以①式两边平方得m2=a,③
②③联立,得m2-2m=0,所以m=0(舍)或m=2,所以a=.
12.设f(x)=|3x-1|,cf(a)>f(b),则下列关系式中一定成立的是( )
A.3c≤3b B.3c>3b
C.3c+3a>2 D.3c+3a<2
【答案】D
【解析】作出函数f(x)=|3x-1|的图象如图所示.
由cf(a)>f(b)可知c,b,a不在同一个单调区间上.∴c<0,a>0.∴f(c)=1-3c,f(a)=3a-1.∵f(c)>f(a),∴1-3c>3a-1,∴3c+3a<2.
13.(一题两空)设函数f(x)=10-ax,a是不为零的常数.
(1)若f(3)=,则使f(x)≥4成立的x的取值范围为________;
(2)当x∈[-1,2]时,f(x)的最大值是16,则a的值为________.
【答案】(1)[4,+∞) (2)-14或7
【解析】(1)由f(3)=得a=3,
∴不等式f(x)≥4可化为23x-10≥22,
由此可得3x-10≥2,∴x≥4,
故x的取值范围是[4,+∞).
(2)当a>0时,f(x)=10-ax=2ax-10是增函数,
则当x∈[-1,2]时,
f(x)max=f(2)=22a-10=16,∴a=7;
当a<0时,f(x)=10-ax=2ax-10是减函数,
则当x∈[-1,2]时,
f(x)max=f(-1)=2-a-10=16,
∴a=-14.综上,a=-14或a=7.
14.某地下车库在排气扇发生故障的情况下,测得空气中一氧化碳的含量达到了危险状态,经抢修后恢复正常.排气4分钟后测得车库内一氧化碳浓度为64 ppm(ppm为浓度单位,1 ppm表示百万分之一),再过4分钟又测得浓度为32 ppm.经检验知,该地下车库一氧化碳浓度y(ppm)与排气时间t(分钟)之间存在函数关系y=cm t(c,m为常数).
(1)求c,m的值;
(2)若空气中一氧化碳浓度不高于0.5 ppm为正常,问至少排气多少分钟才能使这个地下车库中一氧化碳含量达到正常状态?
【解析】(1)由题意可得解得故c,m的值分别为128,.
(2)由(1)知y=128×,令128×≤,即≤,解得t≥32,即至少排气32分钟才能使这个地下车库中一氧化碳含量达到正常状态.
15.定义:对于函数f(x),若在定义域内存在实数x满足f(-x)=-f(x),则称f(x)为“局部奇函数”.若f(x)=2x+m是定义在区间[-1,1]上的“局部奇函数”,求实数m的取值范围.
【解析】法一:f(x)=2x+m,f(-x)=-f(x)可化为2x+2-x+2m=0,
因为f(x)的定义域为[-1,1],
所以方程2x+2-x+2m=0在[-1,1]内有解,
令t=2x,则t∈,故-2m=t+,
设g(t)=t+,则在(0,1]上单调递减,在[1,+∞)上单调递增,
所以当t∈时,g(t)∈,
即-2m∈,
所以m∈.
法二:当f(x)=2x+m时,f(-x)=-f(x)可化为2x+2-x+2m=0,
令t=2x,则t∈,故关于t的二次方程t2+2mt+1=0在上有解即可保证f(x)为“局部奇函数”,设f(t)=t2+2mt+1.
①当方程t2+2mt+1=0在上只有一个解或有两个相同的解时,
需满足或f·f(2)≤0,解得m=-1或m=-,
当m=-时,方程在区间上有两个解,不符合,故m=-1.
②当方程t2+2mt+1=0在上有两个不相等实根时,需满足 故-≤m<-1,综上,m∈.
21世纪教育网(www.21cnjy.com)
4.2.2指数函数的图象和性质
知识点 指数函数的图象和性质
a>1 0
性 质 定义域 R
值域
过定点 过定点 ,即x=0时,y=1
函数值 的变化 当x<0时, 当x>0时,y>1 当x>0时,0
单调性 在R上是增函数 在R上是减函数
对称性 y=ax与y=x的图象关于y轴对称
【思考】
指数函数y=ax(a>0且a≠1)的底数a对图象有哪些影响?
【提示】(1)底数a与1的大小关系决定了指数函数图象的增减性:a>1时,图象单调递增;0<a<1时,图象单调递减.
(2)底数的大小决定了图象相对位置的高低:不论是a>1,还是0<a<1,在第一象限内底数越小,函数图象越靠近x轴;底数越大,函数图象越靠近y轴.
【基础自测】
1.判断正误(正确的画“√”,错误的画“×”)
(1)函数y=x-1的值域是(0,+∞). ( )
(2)已知函数f(x)=x,若实数m,n满足f(m)>f(n),则m>n. ( )
(3)指数函数f(x)的图象过点. ( )
(4)函数y=2的定义域是R. ( )
【答案】(1)×(2)√(3)√(4)×
2.函数y= 的定义域是 ( )
A.[0,+∞) B.(-∞,0]
C.[1,+∞) D.(-∞,+∞)
【答案】B
【解析】∵1-3x≥0,即3x≤1,∴x≤0,即x∈(-∞,0].故选B.
3.函数y=1-2x,x∈[0,1]的值域是 ( )
A.[0,1] B.[-1,0]
C. D.
【答案】B
【解析】由指数函数y=2x在x∈[0,1]上单调递增知1≤2x≤2,∴y=1-2x∈[-1,0].
4.(多选)下列函数中,是增函数的为 ( )
A.y=x B.y=(+1)x
C.y=2-x D.y=(a2+2)x
【答案】BD
题型一 指数函数的定义域和值域
【学透用活】
【例1】求下列函数的定义域和值域:
(1)y=2;(2)y=-|x|;(3)y= .
【解析】(1)x应满足x-4≠0,∴x≠4,
∴定义域为{x|x≠4,x∈R}.
∵≠0,∴2≠1,
∴y=2的值域为{y|y>0,且y≠1}.
(2)定义域为R.
∵|x|≥0,∴y=-|x|=|x|≥0=1,∴此函数的值域为[1,+∞).
(3)由题意知1-x≥0,∴x≤1=0,∴x≥0,
∴定义域为{x|x≥0,x∈R}.
∵x≥0,∴x≤1.
又∵x>0,∴0<x≤1.∴0≤1-x<1,
∴0≤y<1,∴此函数的值域为[0,1).
【方法技巧】
求指数型函数的定义域和值域的一般方法
(1)求与指数函数有关的函数的定义域时,首先观察函数是y=ax型还是y=af(x)型,前者的定义域是R,后者的定义域与f(x)的定义域一致,而求y=型函数的定义域时,往往转化为解指数不等式(组).
(2)求与指数函数有关的函数的值域时,一方面要考虑函数的定义域和单调性,另一方面要注意指数函数的值域是(0,+∞).一般地,对于y=af(x)型函数,应先求出f(x)的值域A,再画出y=ax(x∈A)的图形或利用函数的单调性,就能很容易求出原函数的值域.
【提醒】(1)通过建立不等关系求定义域时,要注意解集为各不等关系解集的交集.
(2)当指数型函数的底数含字母时,在求定义域、值域时要注意分类讨论.
【变式训练】
求下列函数的定义域、值域:
(1)y=;(2)y=2;(3)y=4x-2x+1.
【解析】(1)函数的定义域为R.∵y===1-,
又∵3x>0,∴1+3x>1,∴0<<1,∴-1<-<0,
∴0<1-<1,∴函数的值域为(0,1).
(2)函数的定义域为R.∵2x-x2=-(x-1)2+1≤1,
∴2≤2,即y≤2.又2>0,∴函数的值域为(0,2].
(3)函数的定义域为R. y=(2x)2-2x+1=2+,
∵2x>0,∴当2x=,即x=-1时,y取最小值,
∴函数的值域为.
题型二 指数函数的图象及应用
【学透用活】
1.指数函数图象的特征
同一坐标系中,画出不同底数的指数函数的图象如图所示.
直线x=1与四个指数函数y=ax,y=bx,y=cx,y=dx的交点依次为(1,a),(1,b),(1,c),(1,d),所以有0<b<a<1<d<c,因此可得出以下结论:在y轴的右侧,底数越大,图象越高,简称“底大图高”.
2.指数函数图象的变换
(1)平移规律:设b>0,
①y=ax的图象y=ax+b的图象;
②y=ax的图象y=ax-b的图象;
③y=ax的图象y=ax+b的图象;
④y=ax的图象y=ax-b的图象.
(2)对称规律
y=ax(a>0, 且a≠1)的图象 与y=a-x的图象关于y轴对称
与y=-ax的图象关于x轴对称
与y=-a-x的图象关于坐标原点对称
【例2】 (1)函数y=ax-a(a>0,且a≠1)的图象可能是 ( )
(2)在如图所示的图象中,二次函数y=ax2+bx+c与函数y=x的图象可能是 ( )
【解析】(1)当x=1时,y=a1-a=0,故函数y=ax-a的图象过定点(1,0),结合图象可知选C.
(2)根据图中二次函数图象可知c=0,∴二次函数y=ax2+bx,∵>0,
∴二次函数的对称轴为x=-<0,排除B、D.
对于A、C,都有0<<1,∴-<-<0,C不符合,故选A.
【方法技巧】
指数函数图象问题的处理技巧
(1)抓住图象上的特殊点,如指数函数的图象过定点.
(2)利用图象变换,如函数图象的平移变换(左右平移、上下平移).
(3)利用函数的奇偶性与单调性.奇偶性确定函数的对称情况,单调性决定函数图象的走势.
【变式训练】
1.[图象识别与判断]函数y=a|x|(a>1)的图象是 ( )
【答案】B
【解析】该函数是偶函数.可先画出x≥0时,y=ax的图象,然后沿y
轴翻折过去,便得到x<0时的函数图象.
2.[图象中数据判断问题]函数f(x)=ax-b的图象如图所示,其中a,b为常数,则下列结论正确的是 ( )
A.a>1,b<0 B.a>1,b>0
C.0<a<1,b>0 D.0<a<1,b<0
【答案】D
【解析】从曲线的变化趋势,可以得到函数f(x)为减函数,从而有0<a<1;
从曲线位置看,是由函数y=ax(0<a<1)的图象向左平移|-b|个单位长度得到,所以-b>0,即b<0.
3.[图象过定点问题]已知函数f(x)=ax-16+3(a>0,且a≠1)的图象恒过定点P,若定点P在幂函数g(x)的图象上,则幂函数g(x)的图象是( )
【答案】A
【解析】 f(x)=ax-16+3恒过定点P(16,4),
设幂函数g(x)=xα,则16α=4,∴α=,∴g(x)=.
3.[图象过定点问题]已知函数f(x)=ax-16+3(a>0,且a≠1)的图象恒过
定点P,若定点P在幂函数g(x)的图象上,则幂函数g(x)的图象是
( )
【答案】A
【解析】 f(x)=ax-16+3恒过定点P(16,4),设幂函数g(x)=xα,则16α=4,∴α=,∴g(x)=.
4.[图象的应用]已知直线y=2a与函数y=|2x-2|的图象有两个公共点,
求实数a的取值范围.
【解析】函数y=|2x-2|的图象如图所示.要使直线y=2a与
该图象有两个公共点,则有0<2a<2,即0<a<1,故实
数a的取值范围为(0,1).
题型三 比较大小问题
【探究发现】
(1)函数幂的形式有哪些?
(2)它们的单调性如何判断?
【提示】(1)幂的形式的函数有幂函数和指数函数.
(2)幂函数y=xα,x>0,α>0时为增函数,指数函数y=ax,当a>1时为增函数,当0<a<1时为减函数.
【学透用活】
【例3】比较下列各题中两个值的大小:
(1)1.70.3,0.93.1;(2)-1.8,-2.5;
(3)0.20.3,0.30.2.
【解析】(1)因为1.70.3>1.70=1,0.93.1<0.90=1,
所以1.70.3>0.93.1.
(2)因为0<<1,所以函数y=x在其定义域R上单调递减,又-1.8>-2.5,所以-1.8<-2.5.
(3)因为0<0.2<0.3<1,所以指数函数y=0.2x与y=0.3x在定义域R上均是减函数,且在区间(0,+∞)上函数y=0.2x的图象在函数y=0.3x的图象的下方,所以0.20.2<0.30.2.
又根据指数函数y=0.2x在R上是减函数,可得0.20.3<0.20.2,所以0.20.3<0.30.2.
【方法技巧】
【变式训练】
1.已知a=,b=,c=,则a,b,c的大小关系是 ( )
A.c<a<b B.a<b<c
C.b<a<c D.c<b<a
【答案】D
【解析】 (1)原式=(-1)·+-+1
=+500-10(+2)+1
=+10-10-20+1=-.
(2)原式=(63)+32-(73)-(5-3)=36+9-7-5=33.
(3)3π×π++1=π+22×+1=1π+24+1=18.
2.比较下列各组数的大小:
(1)1.52.5和1.53.2;
(2)0.6-1.2和0.6-1.5;
(3)1.50.3和0.81.2.
【解析】(1)∵函数y=1.5x在R上是增函数,2.5<3.2,∴1.52.5<1.53.2.
(2)∵函数y=0.6x在R上是减函数,-1.2>-1.5,∴0.6-1.2<0.6-1.5.
(3)由指数函数的性质知1.50.3>1.50=1,
而0.81.2<0.80=1,∴1.50.3>0.81.2.
【课堂思维激活】
一、综合性——强调融会贯通
1.已知函数f(x)=ax(a>0,且a≠1).
(1)若f(1)+f(-1)=,求f(2)+f(-2)的值;
(2)若函数f(x)在[-1,1]上的最大值与最小值的差为,求实数a的值.
请根据题设条件把下面的解析补充完整.
【解析】(1)∵f(x)=ax,f(1)+f(-1)=,
∴a+=,解得a=2或,
当a=2时,f(x)=,f(2)+f(-2)=,
当a=时,f(x)=,f(2)+f(-2)=,
故f(2)+f(-2)=.
(2)当a>1时,f(x)=ax在[-1,1]上单调递增,
∴f(x)max-f(x)min=f(1)-f(-1)=a-a-1=,
化简得3a2-8a-3=0,解得a=-(舍去)或a=3.
当0<a<1时,f(x)=ax在[-1,1]上单调递减,
∴f(x)max-f(x)min=f(-1)-f(1)=a-1-a=,化简得3a2+8a-3=0.
解得a=-3(舍去)或a=.
综上,实数a的值为3或.
二、应用性——强调学以致用
2.[好题共享——选自苏教版新教材]有些家用电器(如冰箱等)使用了氟化
物,氟化物的释放破坏了大气上层的臭氧层,使臭氧含量Q呈指数函数型
变化,在氟化物排放量维持某种水平时,具有关系式Q=Q0e-0.002 5t,其中
Q0是臭氧的初始量.
(1)随时间t的增加,臭氧的含量是增加还是减少?
(2)试估计多少年以后将会有一半的臭氧消失.(用计算器计算)
【析题建模】
―→
【解析】(1)Q=Q0e-0.002 5t,∵u=-0.002 5t随t的增大而减少,且e>1,
∴e-0.002 5t的值也随t的增大而减小.
∴随时间t的增加,臭氧的含量减少.
(2)由题意得Q0=Q0e-0.002 5t,即e-0.002 5t=.
借助计算器计算得t≈277.2年,
∴278年后将会有一半的臭氧消失.
三、创新性——强调创新意识和创新思维
3.已知四个函数f(x)=2x,g(x)=x,h(x)=3x,p(x)=x,若y=f(x),y=
g(x)的图象如图所示.
(1)请在如图坐标系中画出y=h(x),y=p(x)的图象,并根据这四个函数的图象
抽象出指数函数具有哪些性质?
(2)举出在实际情境能够抽象出指数函数的一个实例并说明理由.
【解析】(1)画出y=h(x),y=p(x)的图象如图所示:4个
函数都是y=ax(a>0,a≠1)的形式,它们的性质有:
①定义域为R;
②值域为(0,+∞);
③都过定点(0,1);
④当a>1时,函数在定义域内单调递增,0<a<1时,
函数在定义域内单调递减;
⑤a>1时,若x<0,则0<y<1,若x>0,则y>1.
0<a<1时,若x>0,则0<y<1,若x<0,则y>1;
⑥对于函数y=ax(a>0,且a≠1),y=bx(b>0,且b≠1),
当a>b>1时,
若x<0,则0<ax<bx<1;若x=0,则ax=bx=1;
若x>0,则ax>bx>1.
当0<a<b<1时,
若x<0,则ax>bx>1;若x=0,则ax=bx=1;若x>0,则0<ax<bx<1.
(2)举例:原来有一个细胞,细胞分裂的规则是细胞由一个分裂成2个,则经过x次分裂,细胞个数y,
则y=2x,是一个指数函数.
1.函数f(x)=是( )
A.偶函数,在(0,+∞)是增函数
B.奇函数,在(0,+∞)是增函数
C.偶函数,在(0,+∞)是减函数
D.奇函数,在(0,+∞)是减函数
【答案】B
【解析】因为f(-x)=-f(x),所以f(x)为奇函数,
又因为y=2x是增函数,y=2-x为减函数,
故f(x)=为增函数.故选B.
2.(多选)设函数f(x)=a-|x|(a>0,且a≠1),若f(2)=4,则( )
A.f(-2)>f(-1) B.f(-1)>f(-2)
C.f(-2)>f(2) D.f(-4)>f(3)
【答案】AD
【解析】由f(2)=a-2=4得a=,即f(x)=-|x|=2|x|,故f(-2)>f(-1),f(-2)=f(2),f(-4)=f(4)>f(3),所以A、D正确.
3.函数y=ax在[0,1]上的最大值与最小值的和为3,则函数y=2ax-1在[0,1]上的最大值是( )
A.6 B.1
C.3 D.
【答案】C
【解析】函数y=ax在[0,1]上是单调的,最大值与最小值都在端点处取到,故有a0+a1=3,解得a=2,因此函数y=2ax-1=4x-1在[0,1]上是单调递增函数,当x=1时,ymax=3.
4.若函数f(x)=a|2x-4|(a>0,且a≠1)满足f(1)=,则f(x)的单调递减区间是( )
A.(-∞,2] B.[2,+∞)
C.[-2,+∞) D.(-∞,-2]
【答案】B
【解析】由f(1)=,得a2=,于是a=,因此f(x)=|2x-4|.
令t=|2x-4|,∴h(t)=t为减函数.
因为g(x)=|2x-4|在[2,+∞)上单调递增,所以f(x)的单调递减区间是[2,+∞).故选B.
5.若关于x的不等式a2x≥a3-x(0
C.6 D.9
【答案】D
【解析】∵0
【答案】{x|0≤x≤1}
【解析】f(x)≥ 或∴0≤x≤1,
故不等式f(x)≥的解集是{x|0≤x≤1}.
7.春天来了,某池塘中的荷花枝繁叶茂,已知每一天新长出荷叶覆盖水面面积是前一天的2倍,若荷叶20天可以完全长满池塘水面,当荷叶刚好覆盖水面面积一半时,荷叶已生长了________天.
【答案】19
【解析】假设第一天荷叶覆盖水面面积为1,则荷叶覆盖水面面积y与生长时间的函数关系为y=2x-1,因为荷叶20天可以完全长满池塘水面,故当荷叶刚好覆盖水面面积一半时,×220-1=2x-1,解得x=19,所以生长19天时,荷叶布满水面一半.
8.函数f(x)=(a>0,且a≠1)是R上的减函数,则a的取值范围是________.
【答案】
【解析】由单调性定义,f(x)为减函数应满足:即≤a<1.
9.已知指数函数f(x)的图象过点.
(1)求函数f(x)的解析式;
(2)已知f(|x|)>f(1),求x的取值范围.
【解析】(1)设f(x)=ax(a>0,且a≠1).将点代入得=a2.
解得a=.故f(x)=x.
(2)由(1)知f(x)=x,显然f(x)在R上是减函数,又f(|x|)>f(1),所以|x|<1,解得-1
10.对于函数f(x)=a-(x∈R).
(1)判断并证明函数的单调性;
(2)是否存在实数a,使函数f(x)为奇函数?证明你的结论.
【解析】(1)函数f(x)为R上的增函数.证明如下:函数f(x)的定义域为R.任取x1,x2∈R,且x1
证明如下:当a=1时,f(x)=1-=.
对任意x∈R,f(-x)===-=-f(x),又f(x)的定义域为R,故f(x)为奇函数.
11.如图,面积为8的平行四边形OABC的对角线AC⊥CO,AC与BO交于点E.若指数函数y=ax(a>0,且a≠1)的图象经过E,B两点,则a等于( )
A. B.
C.2 D.3
【答案】A
【解析】设点C(0,m)(m>0),则由已知可依次得A,E,B.又因为点E,B在指数函数y=ax的图象上,所以①式两边平方得m2=a,③
②③联立,得m2-2m=0,所以m=0(舍)或m=2,所以a=.
12.设f(x)=|3x-1|,c
A.3c≤3b B.3c>3b
C.3c+3a>2 D.3c+3a<2
【答案】D
【解析】作出函数f(x)=|3x-1|的图象如图所示.
由c
13.(一题两空)设函数f(x)=10-ax,a是不为零的常数.
(1)若f(3)=,则使f(x)≥4成立的x的取值范围为________;
(2)当x∈[-1,2]时,f(x)的最大值是16,则a的值为________.
【答案】(1)[4,+∞) (2)-14或7
【解析】(1)由f(3)=得a=3,
∴不等式f(x)≥4可化为23x-10≥22,
由此可得3x-10≥2,∴x≥4,
故x的取值范围是[4,+∞).
(2)当a>0时,f(x)=10-ax=2ax-10是增函数,
则当x∈[-1,2]时,
f(x)max=f(2)=22a-10=16,∴a=7;
当a<0时,f(x)=10-ax=2ax-10是减函数,
则当x∈[-1,2]时,
f(x)max=f(-1)=2-a-10=16,
∴a=-14.综上,a=-14或a=7.
14.某地下车库在排气扇发生故障的情况下,测得空气中一氧化碳的含量达到了危险状态,经抢修后恢复正常.排气4分钟后测得车库内一氧化碳浓度为64 ppm(ppm为浓度单位,1 ppm表示百万分之一),再过4分钟又测得浓度为32 ppm.经检验知,该地下车库一氧化碳浓度y(ppm)与排气时间t(分钟)之间存在函数关系y=cm t(c,m为常数).
(1)求c,m的值;
(2)若空气中一氧化碳浓度不高于0.5 ppm为正常,问至少排气多少分钟才能使这个地下车库中一氧化碳含量达到正常状态?
【解析】(1)由题意可得解得故c,m的值分别为128,.
(2)由(1)知y=128×,令128×≤,即≤,解得t≥32,即至少排气32分钟才能使这个地下车库中一氧化碳含量达到正常状态.
15.定义:对于函数f(x),若在定义域内存在实数x满足f(-x)=-f(x),则称f(x)为“局部奇函数”.若f(x)=2x+m是定义在区间[-1,1]上的“局部奇函数”,求实数m的取值范围.
【解析】法一:f(x)=2x+m,f(-x)=-f(x)可化为2x+2-x+2m=0,
因为f(x)的定义域为[-1,1],
所以方程2x+2-x+2m=0在[-1,1]内有解,
令t=2x,则t∈,故-2m=t+,
设g(t)=t+,则在(0,1]上单调递减,在[1,+∞)上单调递增,
所以当t∈时,g(t)∈,
即-2m∈,
所以m∈.
法二:当f(x)=2x+m时,f(-x)=-f(x)可化为2x+2-x+2m=0,
令t=2x,则t∈,故关于t的二次方程t2+2mt+1=0在上有解即可保证f(x)为“局部奇函数”,设f(t)=t2+2mt+1.
①当方程t2+2mt+1=0在上只有一个解或有两个相同的解时,
需满足或f·f(2)≤0,解得m=-1或m=-,
当m=-时,方程在区间上有两个解,不符合,故m=-1.
②当方程t2+2mt+1=0在上有两个不相等实根时,需满足 故-≤m<-1,综上,m∈.
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
