4.4.2对数函数的图象和性质(知识梳理+例题+变式+练习)(解析版)
文档属性
| 名称 | 4.4.2对数函数的图象和性质(知识梳理+例题+变式+练习)(解析版) | 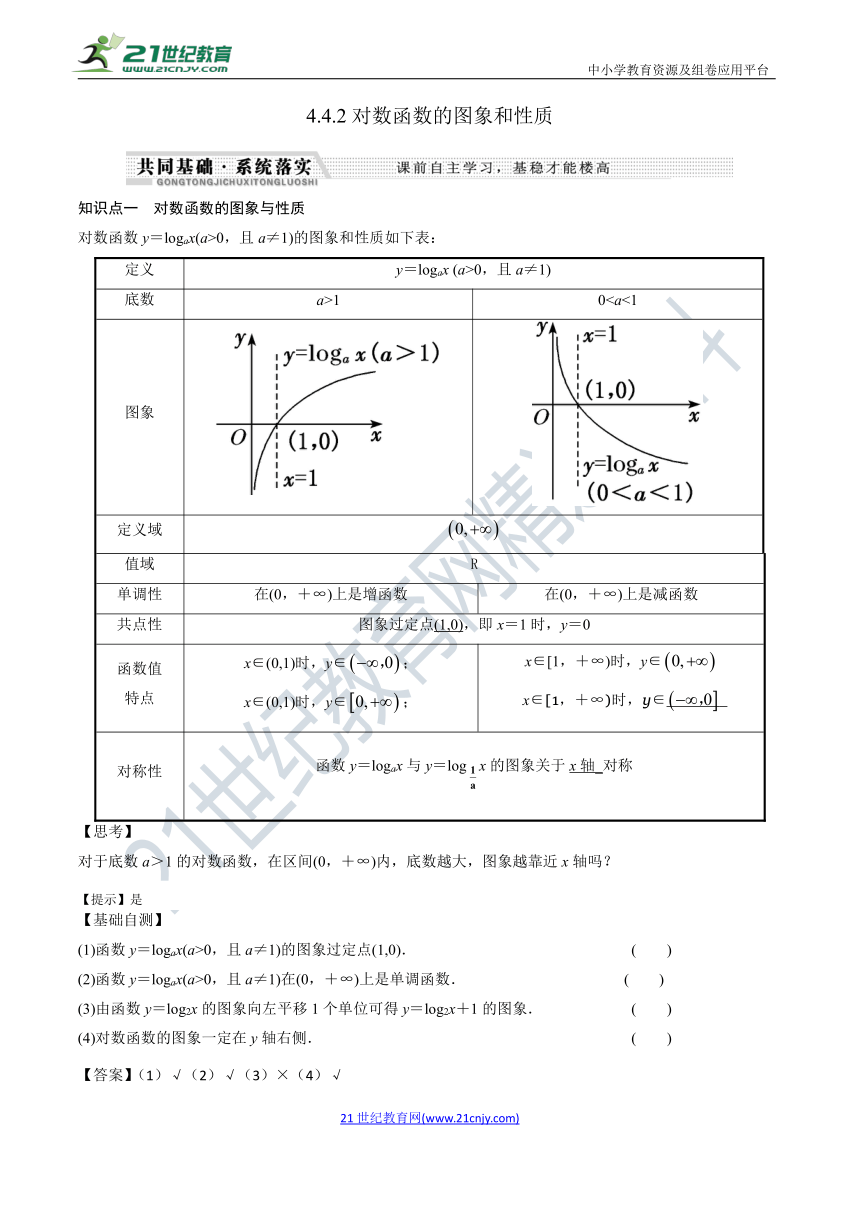 | |
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-28 18:14:19 | ||
图片预览





文档简介
中小学教育资源及组卷应用平台
4.4.2对数函数的图象和性质
知识点一 对数函数的图象与性质
对数函数y=logax(a>0,且a≠1)的图象和性质如下表:
定义 y=logax (a>0,且a≠1)
底数 a>1 0图象
定义域
值域 R
单调性 在(0,+∞)上是增函数 在(0,+∞)上是减函数
共点性 图象过定点(1,0),即x=1时,y=0
函数值 特点 x∈(0,1)时,y∈; x∈(0,1)时,y∈; x∈[1,+∞)时,y∈ x∈[1,+∞)时,y∈
对称性 函数y=logax与y=logx的图象关于x轴_对称
【思考】
对于底数a>1的对数函数,在区间(0,+∞)内,底数越大,图象越靠近x轴吗?
【提示】是
【基础自测】
(1)函数y=logax(a>0,且a≠1)的图象过定点(1,0). ( )
(2)函数y=logax(a>0,且a≠1)在(0,+∞)上是单调函数. ( )
(3)由函数y=log2x的图象向左平移1个单位可得y=log2x+1的图象. ( )
(4)对数函数的图象一定在y轴右侧. ( )
【答案】(1)√(2)√(3)×(4)√
2.函数y=lg(x+1)的图象大致是 ( )
【答案】C
【解析】由底数大于1可排除A、B,y=lg(x+1)可看作是y=lg x的图象向左平移1个单位.(或令x=0得
y=0,而且函数为增函数)
3.函数f(x)=|logx|的单调递增区间是 ( )
A. B.(0,1]
C.(0,+∞) D.[1,+∞)
【答案】D
【解析】作出f(x)的图象如图所示,由图象可知单调递增区间为[1,+∞).
知识点二 反函数
指数函数 (a>0,且a≠1)与对数函数y=logax(a>0,且a≠1)互为反函数,它们的定义域与值域正好互换.
【思考】反函数有哪些性质?
【提示】(1)互为反函数的两个函数图象关于直线y=x对称.
(2)反函数的定义域是原函数的值域,反函数的值域是原函数的定义域.
【基础自测】
1.判断正误
(1)函数y=log2x与y=x2互为反函数. ( )
(2)y=4x与y=log4x的图象关于y=x对称. ( )
【答案】(1)×(2)√
2.若函数y=f(x)是函数y=3x的反函数,则f的值为 ( )
A.-log23 B.-log32
C. D.
【答案】B
【解析】
1.填表,用分数指数幂的形式表示下列各式(a>0).
a2
【答案】
2.3可化为 ( )
A. B. C. D.
【答案】C
【解析】y=f(x)=log3x,∴f=log3=-log32.
题型一 对数函数的图象问题
【学透用活】
(1)底数a与1的大小关系决定了对数函数图象的“升降”
当a>1时,对数函数的图象“上升”;
当0<a<1时,对数函数的图象“下降”.
(2)函数y=logax与y=logx(a>0,且a≠1)的图象关于x轴对称.
(3)底数的大小决定了图象相对位置的高低
无论是a>1还是0<a<1,在第一象限内,自左向右,图象对应的对数函数的底数逐渐变大.
①上下比较:在直线x=1的右侧,a>1时,a越大,图象越靠近x轴;0<a<1时,a越小,图象越靠近x轴;
②左右比较:比较图象与直线y=1的交点,交点的横坐标越大,对应的对数函数的底数越大.
【例1】已知y=lg x的图象,如图所示,由图象作出y=lg |x|和y=|lg x|的图象,并解答以下问题:
(1)判断函数y=lg |x|的奇偶性及单调性.
(2)函数f(x)=|lg x|,若0f(b).证明:ab<1.
【解析】分别作出y=lg |x|和y=|lg x|的图象如图①,图②所示.
(1)从图①可以看出,y=lg|x|是偶函数且在(-∞,0)上单调递减,在(0,+∞)上单调递增.
(2)证明:由图②可以看出,若0f(b),此时有ab<1成立;
若0因为f(a)>f(b),所以-lg a>lg b,
即lg a+lg b<0,lg(ab)<0,所以ab<1;
若1f(b)相矛盾.
综上可知,若0f(b)时,ab<1.
【方法技巧】
有关对数型函数图象问题的应用技巧
(1)求函数y=m+logaf(x)(a>0,且a≠1)的图象过定点时,只需令f(x)=1求出x,即得定点为(x,m).
(2)给出函数解析式判断函数的图象,应首先考虑函数对应的基本初等函数是哪一种;其次找出函数图象的特殊点,判断函数的基本性质,即定义域、单调性以及奇偶性等;最后综合上述几个方面将图象选出,解决此类题目常采用排除法.
(3)根据对数函数图象判断底数大小的方法:作直线y=1与所给图象相交,交点的横坐标即为各个底数,根据在第一象限内,自左向右,图象对应的对数函数的底数逐渐变大,可比较底数的大小.
【变式训练】
1.[函数图象的识别]函数f(x)=lg(|x|-1)的大致图象是( )
【答案】B
【解析】由f(-x)=lg(|-x|-1)=lg(|x|-1)=f(x),得f(x)是偶函数,由此知C、D错误.又当x>0时,f(x)
=lg(x-1)是(1,+∞)上的增函数,故选B.
2.[对数型函数图象的数据分析]如图,若C1,C2分别为函数y=logax和y=logbx的图象,则 ( )
A.0<a<b<1 B.0<b<a<1
C.a>b>1 D.b>a>1
【答案】B
【解析】作直线y=1,则直线与C1,C2的交点的横坐标分别为a,b,易知0<b<a<1.
3.[图象过定点问题]若函数y=loga(x+b)+c(a>0,且a≠1)的图象恒过定点(3,2),则实数b,c的值分别
为________.
【答案】-2,2
【解析】∵函数的图象恒过定点(3,2),∴将(3,2)代入y=loga(x+b)+c,得2=loga(3+b)+c.
又当a>0,且a≠1时,loga1=0恒成立,
∴c=2,3+b=1,∴b=-2,c=2.
4.[作图象并指明性质]画出函数y=|log2(x+1)|的图象,并写出函数的值域及单调区间.
【解析】函数y=|log2(x+1)|的图象如图所示.
由图象知,其值域为[0,+∞),单调递减区间是(-1,0],单调递增区间是(0,+∞).
题型二 比较对数值的大小
【学透用活】
【例2】(1)若a=log23,b=log32,c=log46,则下列结论正确的是( )
A.bC.c(2)下列不等式成立的是(其中a>0,且a≠1) ( )
A.loga5.1log2.2
C.log1.1(a+1)【答案】D B
【解析】 (1)因为函数y=log4x在(0,+∞)上是增函数,所以a=log23=log49>log46>1,又log32<1,所以b(2)对于选项A,因为a和1大小的关系不确定,无法确定对数函数的单调性,故A不成立;对于选项B,因为以为底的对数函数是减函数,所以成立;对于选项C,因为以1.1为底的对数函数是增函数,所以不成立;对于选项D,log32.9>0,log0.52.2<0,故不成立,故选B.
【方法技巧】
比较对数值的大小的策略
(1)比较两个底数为同一常数的对数的大小,首先要根据对数的底数来判断对数函数的单调性,然后比较真数的大小,再利用对数函数的单调性判断.
(2)比较两个对数值的大小,对于底数是相同字母的,需要对底数进行讨论.
(3)若不同底但同真,则可利用图象的位置关系与底数的大小关系解决或利用换底公式化为同底后再进行比较.
(4)若底数和真数都不相同,则常借助中间量1,0,-1等进行比较.
在解决根式与分数指数幂互化的问题时,关键是熟记根式与分数指数幂的转化式子:a=和a==,其中字母a要使式子有意义.
【变式训练】
1.已知实数a=log45,b=0,c=log30.4,则a,b,c的大小关系为 ( )
A.b<c<a B.b<a<c
C.c<a<b D.c<b<a
【答案】D
【解析】由题知,a=log45>1,b=0=1,c=log30.4<0,故c<b<a.
2.已知logm<logn<0,则 ( )
A.n<m<1 B.m<n<1
C.1<m<n D.1<n<m
【解析】因为0<<1,logm<logn<0,所以m>n>1,故选D.
题型三 对数型函数的单调性及应用
【例3】求函数y=log(x2-3x+5)的单调区间.
【解析】由于x2-3x+5的判别式Δ=(-3)2-4×5=-11<0,∴x2-3x+5>0,
令u(x)=x2-3x+5,当x∈时,u(x)为减函数,当x∈时,u(x)为增函数.
∴y=log (x2-3x+5)在上为增函数,在上为减函数.
综上,函数y=log (x2-3x+5)的增区间为,减区间为.
【方法技巧】
形如f(x)=logag(x)(a>0,且a≠1)的函数的单调区间的求法:
(1)先求g(x)>0的解集(也就是函数f(x)的定义域).
(2)当底数a>1时,在g(x)>0这一前提下,g(x)的单调增区间是f(x)的单调增区间;g(x)的单调减区间是f(x)的单调减区间.
(3)当底数0<a<1时,在g(x)>0这一前提下,g(x)的单调增区间是f(x)的单调减区间,g(x)的单调减区间是f(x)的单调增区间.
【变式训练】
1.[变条件]本例条件变为y=log(1-x2),问题不变.
【解析】由条件知1-x2>0,∴-1<x<1.
令t=1-x2,x∈(-1,1).
当x∈(-1,0]时,x增大t增大,y=logt减少.
∴x∈(-1,0]时,y=log (1-x2)是减函数.
同理,x∈[0,1)时,y=log (1-x2)是增函数.
故y=log (1-x2)的增区间为[0,1),减区间为(-1,0].
2.已知函数f(x)=lg(x2-2ax-a)在区间(-∞,-3)上是减函数,求实数a的取值范围.
【解析】设u(x)=x2-2ax-a.∵f(x)在(-∞,-3)上是减函数,
∴u(x)在(-∞,-3)上是减函数,且u(x)>0在(-∞,-3)上恒成立.
又u(x)=(x-a)2-a-a2在(-∞,a)上是减函数.
∴解得a≥-.
∴满足条件的实数a的取值范围是[-,+∞).
【课堂思维激活】
一、综合性——强调融会贯通
1.已知函数f(x)=logax(a>0,且a≠1)在[2,4]上的最大值与最小值差
为1,求a的值时,有位同学的解题过程如下:
解:∵x∈[2,4],
∴f(x)的最大值为f(4)=loga4,最小值为f(2)=loga2,
∴loga4-loga2=1,即loga2=1,解得a=2.
这位同学的思路是否正确,如果不正确请改正
【提示】他的思路是错误的
【正解】(1)当a>1时,函数y=logax在[2,4]上是增函数,
∴loga4-loga2=1,即loga=1,∴a=2.
(2)当0<a<1时,函数y=logax在[2,4]上是减函数,
∴loga2-loga4=1,即loga=1,∴a=.
综上知,a=2或a=.
二、应用性——强调学以致用
2.溶液酸碱度是通过pH刻画的.pH的计算公式为pH=-lg[H+],其中[H+]表示溶液中氢离子的浓度,
单位是摩尔/升.
(1)根据对数函数性质及上述pH的计算公式,说明溶液酸碱度与溶液中氢离子的浓度之间的变化关系;
(2)国家标准规定,饮用纯净水的pH应该在[5,7]之间.食品监督部门检测到某品牌纯净水中氢离子浓度为
[H+]=10-7摩尔/升,问该品牌纯净水是否符合国家标准.
【析题建模】
(1)
(2)
【解析】【解析】(1)根据对数的运算性质,有pH=-lg[H+]=lg [H+]-1=lg,在(0,+∞)上,
随着[H+]的增大,减小,相应的lg也减小,即pH减小,所以随着[H+]的增大,pH减小,即溶液
中氢离子的浓度越大,溶液的酸性就越强;同理:溶液中氢离子的浓度越小,溶液的碱性就越强.
(2)当氢离子浓度为[H+]=10-7摩尔/升,纯净水的pH=-lg(10-7)=7,所以该品牌纯净水符合国家标准.
三、创新性——强调创新意识和创新思维
3.[好题共享——选自苏教版新教材]对于等式ab=c(a>0,且a≠1),如果将a视为自变量x,b视为常数,
c为关于a(即x)的函数,记为y,那么y=xb,是幂函数;如果将a视为常数,b视为自变量x,c为关于b(即
x)的函数,记为y,那么y=ax,是指数函数;如果将a视为常数,c视为自变量x,b为关于c(即x)的函数,
记为y,那么y=logax,是对数函数.
事实上,由这个等式还可以得到更多的函数模型.
例如,如果c为常数e(e为自然对数的底数),将a视为自变量x(x>0,x≠1),则b为x的函数,记为y,那么xy=e.
(1)试将y表示成x的函数f(x);
(2)研究函数f(x)的性质.
你还能运用这个等式得到什么样的函数?这些函数分别具有哪些性质?
【解析】 (1)易知f(x)=.
(2)函数f(x)的定义域为(0,1)∪(1,+∞);值域为(-∞,0)∪(0,+∞).
单调性:在(0,1)上单调递减,在(1,+∞)上单调递减.
函数1:在ab=c中,令c=e,b=x视为自变量(x≠0),a=y为关于x的函数.则yx=e y=(x≠0).
此函数的定义域为(-∞,0)∪(0,+∞),值域为(0,1)∪(1,+∞).
单调性:在(-∞,0)上单调递减,在(0,+∞)上单调递减.
函数2:在ab=c中,将c视为自变量x,b视为常数3,a=y(a>0,且a≠1)视为关于x的函数.
则y3=x,y=,定义域为(0,1)∪(1,+∞),值域为(0,1)∪(1,+∞),在(0,1),(1,+∞)上单调递增.
1.已知函数f(x)=log2(1+2-x),则函数f(x)的值域是( )
A.[0,2) B.(0,+∞)
C.(0,2) D.[0,+∞)
【答案】B
【解析】f(x)=log2(1+2-x),∵1+2-x>1,∴log2(1+2-x)>0,∴函数f(x)的值域是(0,+∞),故选B.
2.已知实数a=log45,b=0,c=log30.4,则a,b,c的大小关系为( )
A.b<c<a B.b<a<c
C.c<a<b D.c<b<a
【答案】D
【解析】由题知,a=log45>1,b=0=1,c=log30.4<0,故c<b<a.
3.函数f(x)=|logx|的单调递增区间是( )
A. B.(0,1]
C.(0,+∞) D.[1,+∞)
【答案】D
【解析】f(x)的图象如图所示,由图象可知单调递增区间为[1,+∞).
4.已知logmA.nC.1【答案】D
【解析】因为0<<1,logmn>1,故选D.
5.若函数f(x)=loga|x+1|在(-1,0)上有f(x)>0,则f(x)( )
A.在(-∞,0)上是增函数
B.在(-∞,0)上是减函数
C.在(-∞,-1)上是增函数
D.在(-∞,-1)上是减函数
【答案】C
【解析】当-1∵loga|x+1|>0,∴0∴函数f(x)=loga|x+1|在(-∞,-1)上递增,在(-1,+∞)上递减.
6.设f(x)=lg x,若f(1-a)-f(a)>0,则实数a的取值范围为________.
【答案】
【解析】由题意,f(x)=lg x在(0,+∞)上单调递增,因为f(1-a)-f(a)>0,所以1-a>a>0,所以a∈.
7.已知函数y=loga(2-ax)在[0,1]上是减函数,则实数a的取值范围是________.
【答案】 (1,2)
【解析】令u=2-ax,则y=logau,因为a>0,所以u=2-ax递减,由题意知y=logau在[0,1]内递增,所以a>1.又u=2-ax在x∈[0,1]上恒大于0,所以2-a>0,即a<2,综上,1<a<2.
8.已知a>0且a≠1,若函数f(x)=的值域为[1,+∞),则a的取值范围是________.
【答案】 (1,2]
【解析】若函数f(x)=的值域为[1,+∞),且a>0,a≠1,当x≤2时,y=3-x≥1,所以可得19.根据函数f(x)=log2x的图象与性质解决以下问题.
(1)若f(a)>f(2),求a的取值范围;
(2)求y=log2(2x-1)在x∈[1,14]上的最值.
【解析】函数y=log2x的图象如图.
(1)y=log2x是增函数,若f(a)>f(2),即log2a>log22,则a>2.
∴a的取值范围为(2,+∞).
(2)∵1≤x≤14,∴1≤2x-1≤27,
∴0≤log2(2x-1)≤log227.
∴函数y=log2(2x-1)在x∈[1,14]上的最小值为0,最大值为log227.
10. 已知指数函数f(x)=ax(a>0,且a≠1).
(1)求函数f(x)的反函数g(x)的解析式;
(2)解不等式:g(x)≤loga(2-3x).
【解析】(1)令y=ax(a>0,且a≠1),则x=logay(a>0,且a≠1),所以函数f(x)的反函数为g(x)=logax(a>0,且a≠1).
(2)当a>1时,logax≤loga(2-3x),所以解得0<x≤.
当0<a<1时,原不等式等价于解得≤x<.
综上,当a>1时,原不等式的解集为;
当0<a<1时,原不等式的解集为.
15.某学校为了加强学生数学核心素养的培养,锻炼学生自主探究学习的能力,他们以函数f(x)=lg 为基本素材,研究该函数的相关性质,取得部分研究成果如下:
①同学甲发现:函数f(x)的定义域为(-1,1);
②同学乙发现:函数f(x)是偶函数;
③同学丙发现:对于任意的x∈(-1,1)都有f=2f(x);
④同学丁发现:对于任意的a,b∈(-1,1),都有f(a)+f(b)=f;
⑤同学戊发现:对于函数f(x)定义域中任意的两个不同实数x1,x2,总满足>0.
其中所有正确研究成果的序号是__________.
【答案】①③④
【解析】在①中,因为f(x)=lg ,所以>0,解得函数的定义域为(-1,1),所以①是正确的;在②中,f(x)=lg =-lg =-f(-x),所以函数f(x)为奇函数,所以②是错误的;在③中,对于任意x∈(-1,1),有f=lg=lg =lg ,又2f(x)=2lg =lg ,所以③是正确的;在④中,对于任意的a,b∈(-1,1),有f(a)+f(b)=lg +lg=lg=lg,又f=lg =lg,所以④是正确的;在⑤中,对于函数f(x)的定义域中任意的两个不同实数x1,x2,总满足>0,即说明f(x)是单调递增函数,但f(x)=lg =lg是减函数,所以⑤是错误的.综上可知,正确研究成果的序号为①③④.
21世纪教育网(www.21cnjy.com)
4.4.2对数函数的图象和性质
知识点一 对数函数的图象与性质
对数函数y=logax(a>0,且a≠1)的图象和性质如下表:
定义 y=logax (a>0,且a≠1)
底数 a>1 0
定义域
值域 R
单调性 在(0,+∞)上是增函数 在(0,+∞)上是减函数
共点性 图象过定点(1,0),即x=1时,y=0
函数值 特点 x∈(0,1)时,y∈; x∈(0,1)时,y∈; x∈[1,+∞)时,y∈ x∈[1,+∞)时,y∈
对称性 函数y=logax与y=logx的图象关于x轴_对称
【思考】
对于底数a>1的对数函数,在区间(0,+∞)内,底数越大,图象越靠近x轴吗?
【提示】是
【基础自测】
(1)函数y=logax(a>0,且a≠1)的图象过定点(1,0). ( )
(2)函数y=logax(a>0,且a≠1)在(0,+∞)上是单调函数. ( )
(3)由函数y=log2x的图象向左平移1个单位可得y=log2x+1的图象. ( )
(4)对数函数的图象一定在y轴右侧. ( )
【答案】(1)√(2)√(3)×(4)√
2.函数y=lg(x+1)的图象大致是 ( )
【答案】C
【解析】由底数大于1可排除A、B,y=lg(x+1)可看作是y=lg x的图象向左平移1个单位.(或令x=0得
y=0,而且函数为增函数)
3.函数f(x)=|logx|的单调递增区间是 ( )
A. B.(0,1]
C.(0,+∞) D.[1,+∞)
【答案】D
【解析】作出f(x)的图象如图所示,由图象可知单调递增区间为[1,+∞).
知识点二 反函数
指数函数 (a>0,且a≠1)与对数函数y=logax(a>0,且a≠1)互为反函数,它们的定义域与值域正好互换.
【思考】反函数有哪些性质?
【提示】(1)互为反函数的两个函数图象关于直线y=x对称.
(2)反函数的定义域是原函数的值域,反函数的值域是原函数的定义域.
【基础自测】
1.判断正误
(1)函数y=log2x与y=x2互为反函数. ( )
(2)y=4x与y=log4x的图象关于y=x对称. ( )
【答案】(1)×(2)√
2.若函数y=f(x)是函数y=3x的反函数,则f的值为 ( )
A.-log23 B.-log32
C. D.
【答案】B
【解析】
1.填表,用分数指数幂的形式表示下列各式(a>0).
a2
【答案】
2.3可化为 ( )
A. B. C. D.
【答案】C
【解析】y=f(x)=log3x,∴f=log3=-log32.
题型一 对数函数的图象问题
【学透用活】
(1)底数a与1的大小关系决定了对数函数图象的“升降”
当a>1时,对数函数的图象“上升”;
当0<a<1时,对数函数的图象“下降”.
(2)函数y=logax与y=logx(a>0,且a≠1)的图象关于x轴对称.
(3)底数的大小决定了图象相对位置的高低
无论是a>1还是0<a<1,在第一象限内,自左向右,图象对应的对数函数的底数逐渐变大.
①上下比较:在直线x=1的右侧,a>1时,a越大,图象越靠近x轴;0<a<1时,a越小,图象越靠近x轴;
②左右比较:比较图象与直线y=1的交点,交点的横坐标越大,对应的对数函数的底数越大.
【例1】已知y=lg x的图象,如图所示,由图象作出y=lg |x|和y=|lg x|的图象,并解答以下问题:
(1)判断函数y=lg |x|的奇偶性及单调性.
(2)函数f(x)=|lg x|,若0
【解析】分别作出y=lg |x|和y=|lg x|的图象如图①,图②所示.
(1)从图①可以看出,y=lg|x|是偶函数且在(-∞,0)上单调递减,在(0,+∞)上单调递增.
(2)证明:由图②可以看出,若0
若0
即lg a+lg b<0,lg(ab)<0,所以ab<1;
若1
综上可知,若0
【方法技巧】
有关对数型函数图象问题的应用技巧
(1)求函数y=m+logaf(x)(a>0,且a≠1)的图象过定点时,只需令f(x)=1求出x,即得定点为(x,m).
(2)给出函数解析式判断函数的图象,应首先考虑函数对应的基本初等函数是哪一种;其次找出函数图象的特殊点,判断函数的基本性质,即定义域、单调性以及奇偶性等;最后综合上述几个方面将图象选出,解决此类题目常采用排除法.
(3)根据对数函数图象判断底数大小的方法:作直线y=1与所给图象相交,交点的横坐标即为各个底数,根据在第一象限内,自左向右,图象对应的对数函数的底数逐渐变大,可比较底数的大小.
【变式训练】
1.[函数图象的识别]函数f(x)=lg(|x|-1)的大致图象是( )
【答案】B
【解析】由f(-x)=lg(|-x|-1)=lg(|x|-1)=f(x),得f(x)是偶函数,由此知C、D错误.又当x>0时,f(x)
=lg(x-1)是(1,+∞)上的增函数,故选B.
2.[对数型函数图象的数据分析]如图,若C1,C2分别为函数y=logax和y=logbx的图象,则 ( )
A.0<a<b<1 B.0<b<a<1
C.a>b>1 D.b>a>1
【答案】B
【解析】作直线y=1,则直线与C1,C2的交点的横坐标分别为a,b,易知0<b<a<1.
3.[图象过定点问题]若函数y=loga(x+b)+c(a>0,且a≠1)的图象恒过定点(3,2),则实数b,c的值分别
为________.
【答案】-2,2
【解析】∵函数的图象恒过定点(3,2),∴将(3,2)代入y=loga(x+b)+c,得2=loga(3+b)+c.
又当a>0,且a≠1时,loga1=0恒成立,
∴c=2,3+b=1,∴b=-2,c=2.
4.[作图象并指明性质]画出函数y=|log2(x+1)|的图象,并写出函数的值域及单调区间.
【解析】函数y=|log2(x+1)|的图象如图所示.
由图象知,其值域为[0,+∞),单调递减区间是(-1,0],单调递增区间是(0,+∞).
题型二 比较对数值的大小
【学透用活】
【例2】(1)若a=log23,b=log32,c=log46,则下列结论正确的是( )
A.b
A.loga5.1
C.log1.1(a+1)
【解析】 (1)因为函数y=log4x在(0,+∞)上是增函数,所以a=log23=log49>log46>1,又log32<1,所以b
【方法技巧】
比较对数值的大小的策略
(1)比较两个底数为同一常数的对数的大小,首先要根据对数的底数来判断对数函数的单调性,然后比较真数的大小,再利用对数函数的单调性判断.
(2)比较两个对数值的大小,对于底数是相同字母的,需要对底数进行讨论.
(3)若不同底但同真,则可利用图象的位置关系与底数的大小关系解决或利用换底公式化为同底后再进行比较.
(4)若底数和真数都不相同,则常借助中间量1,0,-1等进行比较.
在解决根式与分数指数幂互化的问题时,关键是熟记根式与分数指数幂的转化式子:a=和a==,其中字母a要使式子有意义.
【变式训练】
1.已知实数a=log45,b=0,c=log30.4,则a,b,c的大小关系为 ( )
A.b<c<a B.b<a<c
C.c<a<b D.c<b<a
【答案】D
【解析】由题知,a=log45>1,b=0=1,c=log30.4<0,故c<b<a.
2.已知logm<logn<0,则 ( )
A.n<m<1 B.m<n<1
C.1<m<n D.1<n<m
【解析】因为0<<1,logm<logn<0,所以m>n>1,故选D.
题型三 对数型函数的单调性及应用
【例3】求函数y=log(x2-3x+5)的单调区间.
【解析】由于x2-3x+5的判别式Δ=(-3)2-4×5=-11<0,∴x2-3x+5>0,
令u(x)=x2-3x+5,当x∈时,u(x)为减函数,当x∈时,u(x)为增函数.
∴y=log (x2-3x+5)在上为增函数,在上为减函数.
综上,函数y=log (x2-3x+5)的增区间为,减区间为.
【方法技巧】
形如f(x)=logag(x)(a>0,且a≠1)的函数的单调区间的求法:
(1)先求g(x)>0的解集(也就是函数f(x)的定义域).
(2)当底数a>1时,在g(x)>0这一前提下,g(x)的单调增区间是f(x)的单调增区间;g(x)的单调减区间是f(x)的单调减区间.
(3)当底数0<a<1时,在g(x)>0这一前提下,g(x)的单调增区间是f(x)的单调减区间,g(x)的单调减区间是f(x)的单调增区间.
【变式训练】
1.[变条件]本例条件变为y=log(1-x2),问题不变.
【解析】由条件知1-x2>0,∴-1<x<1.
令t=1-x2,x∈(-1,1).
当x∈(-1,0]时,x增大t增大,y=logt减少.
∴x∈(-1,0]时,y=log (1-x2)是减函数.
同理,x∈[0,1)时,y=log (1-x2)是增函数.
故y=log (1-x2)的增区间为[0,1),减区间为(-1,0].
2.已知函数f(x)=lg(x2-2ax-a)在区间(-∞,-3)上是减函数,求实数a的取值范围.
【解析】设u(x)=x2-2ax-a.∵f(x)在(-∞,-3)上是减函数,
∴u(x)在(-∞,-3)上是减函数,且u(x)>0在(-∞,-3)上恒成立.
又u(x)=(x-a)2-a-a2在(-∞,a)上是减函数.
∴解得a≥-.
∴满足条件的实数a的取值范围是[-,+∞).
【课堂思维激活】
一、综合性——强调融会贯通
1.已知函数f(x)=logax(a>0,且a≠1)在[2,4]上的最大值与最小值差
为1,求a的值时,有位同学的解题过程如下:
解:∵x∈[2,4],
∴f(x)的最大值为f(4)=loga4,最小值为f(2)=loga2,
∴loga4-loga2=1,即loga2=1,解得a=2.
这位同学的思路是否正确,如果不正确请改正
【提示】他的思路是错误的
【正解】(1)当a>1时,函数y=logax在[2,4]上是增函数,
∴loga4-loga2=1,即loga=1,∴a=2.
(2)当0<a<1时,函数y=logax在[2,4]上是减函数,
∴loga2-loga4=1,即loga=1,∴a=.
综上知,a=2或a=.
二、应用性——强调学以致用
2.溶液酸碱度是通过pH刻画的.pH的计算公式为pH=-lg[H+],其中[H+]表示溶液中氢离子的浓度,
单位是摩尔/升.
(1)根据对数函数性质及上述pH的计算公式,说明溶液酸碱度与溶液中氢离子的浓度之间的变化关系;
(2)国家标准规定,饮用纯净水的pH应该在[5,7]之间.食品监督部门检测到某品牌纯净水中氢离子浓度为
[H+]=10-7摩尔/升,问该品牌纯净水是否符合国家标准.
【析题建模】
(1)
(2)
【解析】【解析】(1)根据对数的运算性质,有pH=-lg[H+]=lg [H+]-1=lg,在(0,+∞)上,
随着[H+]的增大,减小,相应的lg也减小,即pH减小,所以随着[H+]的增大,pH减小,即溶液
中氢离子的浓度越大,溶液的酸性就越强;同理:溶液中氢离子的浓度越小,溶液的碱性就越强.
(2)当氢离子浓度为[H+]=10-7摩尔/升,纯净水的pH=-lg(10-7)=7,所以该品牌纯净水符合国家标准.
三、创新性——强调创新意识和创新思维
3.[好题共享——选自苏教版新教材]对于等式ab=c(a>0,且a≠1),如果将a视为自变量x,b视为常数,
c为关于a(即x)的函数,记为y,那么y=xb,是幂函数;如果将a视为常数,b视为自变量x,c为关于b(即
x)的函数,记为y,那么y=ax,是指数函数;如果将a视为常数,c视为自变量x,b为关于c(即x)的函数,
记为y,那么y=logax,是对数函数.
事实上,由这个等式还可以得到更多的函数模型.
例如,如果c为常数e(e为自然对数的底数),将a视为自变量x(x>0,x≠1),则b为x的函数,记为y,那么xy=e.
(1)试将y表示成x的函数f(x);
(2)研究函数f(x)的性质.
你还能运用这个等式得到什么样的函数?这些函数分别具有哪些性质?
【解析】 (1)易知f(x)=.
(2)函数f(x)的定义域为(0,1)∪(1,+∞);值域为(-∞,0)∪(0,+∞).
单调性:在(0,1)上单调递减,在(1,+∞)上单调递减.
函数1:在ab=c中,令c=e,b=x视为自变量(x≠0),a=y为关于x的函数.则yx=e y=(x≠0).
此函数的定义域为(-∞,0)∪(0,+∞),值域为(0,1)∪(1,+∞).
单调性:在(-∞,0)上单调递减,在(0,+∞)上单调递减.
函数2:在ab=c中,将c视为自变量x,b视为常数3,a=y(a>0,且a≠1)视为关于x的函数.
则y3=x,y=,定义域为(0,1)∪(1,+∞),值域为(0,1)∪(1,+∞),在(0,1),(1,+∞)上单调递增.
1.已知函数f(x)=log2(1+2-x),则函数f(x)的值域是( )
A.[0,2) B.(0,+∞)
C.(0,2) D.[0,+∞)
【答案】B
【解析】f(x)=log2(1+2-x),∵1+2-x>1,∴log2(1+2-x)>0,∴函数f(x)的值域是(0,+∞),故选B.
2.已知实数a=log45,b=0,c=log30.4,则a,b,c的大小关系为( )
A.b<c<a B.b<a<c
C.c<a<b D.c<b<a
【答案】D
【解析】由题知,a=log45>1,b=0=1,c=log30.4<0,故c<b<a.
3.函数f(x)=|logx|的单调递增区间是( )
A. B.(0,1]
C.(0,+∞) D.[1,+∞)
【答案】D
【解析】f(x)的图象如图所示,由图象可知单调递增区间为[1,+∞).
4.已知logm
【解析】因为0<<1,logm
5.若函数f(x)=loga|x+1|在(-1,0)上有f(x)>0,则f(x)( )
A.在(-∞,0)上是增函数
B.在(-∞,0)上是减函数
C.在(-∞,-1)上是增函数
D.在(-∞,-1)上是减函数
【答案】C
【解析】当-1
6.设f(x)=lg x,若f(1-a)-f(a)>0,则实数a的取值范围为________.
【答案】
【解析】由题意,f(x)=lg x在(0,+∞)上单调递增,因为f(1-a)-f(a)>0,所以1-a>a>0,所以a∈.
7.已知函数y=loga(2-ax)在[0,1]上是减函数,则实数a的取值范围是________.
【答案】 (1,2)
【解析】令u=2-ax,则y=logau,因为a>0,所以u=2-ax递减,由题意知y=logau在[0,1]内递增,所以a>1.又u=2-ax在x∈[0,1]上恒大于0,所以2-a>0,即a<2,综上,1<a<2.
8.已知a>0且a≠1,若函数f(x)=的值域为[1,+∞),则a的取值范围是________.
【答案】 (1,2]
【解析】若函数f(x)=的值域为[1,+∞),且a>0,a≠1,当x≤2时,y=3-x≥1,所以可得1
(1)若f(a)>f(2),求a的取值范围;
(2)求y=log2(2x-1)在x∈[1,14]上的最值.
【解析】函数y=log2x的图象如图.
(1)y=log2x是增函数,若f(a)>f(2),即log2a>log22,则a>2.
∴a的取值范围为(2,+∞).
(2)∵1≤x≤14,∴1≤2x-1≤27,
∴0≤log2(2x-1)≤log227.
∴函数y=log2(2x-1)在x∈[1,14]上的最小值为0,最大值为log227.
10. 已知指数函数f(x)=ax(a>0,且a≠1).
(1)求函数f(x)的反函数g(x)的解析式;
(2)解不等式:g(x)≤loga(2-3x).
【解析】(1)令y=ax(a>0,且a≠1),则x=logay(a>0,且a≠1),所以函数f(x)的反函数为g(x)=logax(a>0,且a≠1).
(2)当a>1时,logax≤loga(2-3x),所以解得0<x≤.
当0<a<1时,原不等式等价于解得≤x<.
综上,当a>1时,原不等式的解集为;
当0<a<1时,原不等式的解集为.
15.某学校为了加强学生数学核心素养的培养,锻炼学生自主探究学习的能力,他们以函数f(x)=lg 为基本素材,研究该函数的相关性质,取得部分研究成果如下:
①同学甲发现:函数f(x)的定义域为(-1,1);
②同学乙发现:函数f(x)是偶函数;
③同学丙发现:对于任意的x∈(-1,1)都有f=2f(x);
④同学丁发现:对于任意的a,b∈(-1,1),都有f(a)+f(b)=f;
⑤同学戊发现:对于函数f(x)定义域中任意的两个不同实数x1,x2,总满足>0.
其中所有正确研究成果的序号是__________.
【答案】①③④
【解析】在①中,因为f(x)=lg ,所以>0,解得函数的定义域为(-1,1),所以①是正确的;在②中,f(x)=lg =-lg =-f(-x),所以函数f(x)为奇函数,所以②是错误的;在③中,对于任意x∈(-1,1),有f=lg=lg =lg ,又2f(x)=2lg =lg ,所以③是正确的;在④中,对于任意的a,b∈(-1,1),有f(a)+f(b)=lg +lg=lg=lg,又f=lg =lg,所以④是正确的;在⑤中,对于函数f(x)的定义域中任意的两个不同实数x1,x2,总满足>0,即说明f(x)是单调递增函数,但f(x)=lg =lg是减函数,所以⑤是错误的.综上可知,正确研究成果的序号为①③④.
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
